NCERT कक्षा 6 गणित अध्याय 14 प्रायोगिक ज्यामिति
Ex 14.1
प्रश्न 1.
3.2 सेमी त्रिज्या वाला एक वृत्त खींचिए।
हल:
चरण I: बिंदु O को केंद्र मानकर चिन्हित कीजिए।
चरण II: परकार को दी गई त्रिज्या 3.2 सेमी तक खोलिए।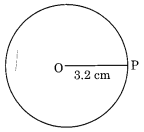
चरण III: परकार की सुई को केंद्र O पर रखिए।
चरण IV: परकार के अग्रभाग को पकड़कर पेंसिल से एक चक्कर लगाइए। इस प्रकार प्राप्त आकृति 3.2 सेमी त्रिज्या वाला अभीष्ट वृत्त है।
प्रश्न 2.
एक ही केंद्र O लेकर, 4 सेमी और 2.5 सेमी त्रिज्या वाले दो वृत्त खींचिए।
हल:
चरण I: केंद्र O लेकर परकार को 4 सेमी तक खोलिए।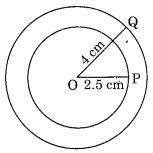
चरण II: सुई को O पर स्थिर रखते हुए एक वृत्त खींचिए।
चरण III: केंद्र O लेकर, परकार को 2.5 सेमी तक खोलिए और एक और वृत्त खींचिए।
आकृति एक ही केंद्र वाले दो अभीष्ट वृत्तों को दर्शाती है।
प्रश्न 3.
एक वृत्त और उसके कोई दो व्यास खींचिए। यदि आप इन व्यासों के सिरों को मिला दें, तो क्या आकृति प्राप्त होगी? यदि व्यास एक दूसरे के लंबवत हैं, तो क्या आकृति प्राप्त होगी? आप अपने उत्तर की जाँच कैसे करेंगे?
हल: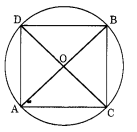
(i) उपयुक्त त्रिज्या वाला केंद्र 0 वाला एक वृत्त खींचिए।
(ii) AB और CD कोई दो व्यास हैं।
(iii) व्यासों के अंतिम बिंदुओं को मिलाने पर, हमें एक चतुर्भुज ACBD प्राप्त होता है।
(iv) हम देखते हैं कि OA = OB = OC = OD [समान त्रिज्या]
और AC = DB, AD = BC
∠A = ∠C = ∠B = ∠D = 90°
इस प्रकार ACBD एक आयत है।
पुनः यदि व्यास एक दूसरे के लंबवत हैं, तो मापने पर, हमें
AC = DB = AD = BC प्राप्त होता है
। इस प्रकार, ACBD एक वर्ग है।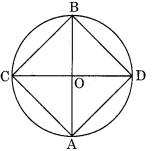
प्रश्न 4.
कोई भी वृत्त खींचिए और उस पर बिंदु A, B और C इस प्रकार अंकित कीजिए कि
(a) A वृत्त पर हो
(b) B वृत्त के अभ्यंतर में हो
(c) C वृत्त के बहिर्भाग में हो।
हल:
केंद्र 0 और एक उपयुक्त त्रिज्या लेकर एक वृत्त खींचिए।
यहाँ
(a) A वृत्त पर है।
(b) B वृत्त के अभ्यंतर में है।
(c) C वृत्त के बहिर्भाग में है।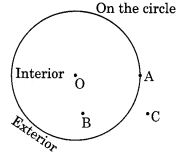
प्रश्न 5.
मान लीजिए A और B समान त्रिज्याओं वाले दो वृत्तों के केंद्र हैं। इन्हें इस प्रकार खींचिए कि प्रत्येक वृत्त दूसरे के केंद्र से होकर जाए। मान लीजिए ये C और D पर प्रतिच्छेद करते हैं।
जाँच कीजिए कि क्या \(\overline { AB }\) और \(\overline { CD }\) समकोण पर हैं। हल: दी गई आकृति में, समान त्रिज्याओं वाले दो वृत्त एक दूसरे को C और D पर प्रतिच्छेद करते हैं। मापने पर, हम देखते हैं कि \(\overline { AB }\) और \(\overline { CD }\) एक दूसरे को समकोण पर प्रतिच्छेद करते हैं।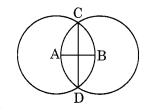
Ex 14.2
प्रश्न 1.
रूलर की सहायता से 7.3 cm लंबाई का एक रेखाखंड खींचिए।
हल:
चरण I: बिंदु P पर निशान लगाइए।
चरण II: रूलर का O चिह्न बिंदु P के सम्मुख रखिए।
चरण III: P से 7.3 cm की दूरी पर एक बिंदु Q अंकित कीजिए।
चरण IV: P और Q को मिलाइए।![]()
इस प्रकार
प्रश्न 2.
रूलर और परकार की सहायता से 5.6 सेमी लंबाई का एक रेखाखंड खींचिए।
हल:
चरण I: उपयुक्त लंबाई की कोई भी रेखा L खींचिए।
चरण II: परकार की सुई को रूलर के शून्य चिह्न पर रखिए और इसे 5.6 चिह्न तक खोलिए।
चरण III: सुई को रेखा के किसी भी बिंदु A पर रखिए और l को B पर काटने के लिए एक चाप लगाइए।![]()
इस प्रकार,
प्रश्न 3.
7.8 सेमी लंबाई की
हल:
दिया गया है कि
चरण I : रूलर का शून्य चिह्न A पर रखिए।
चरण II : A से 7.8 सेमी की दूरी पर एक बिंदु B अंकित कीजिए।
चरण III : A से 4.7 सेमी की दूरी पर एक और बिंदु C इस प्रकार अंकित कीजिए कि AC = 4.7 सेमी हो।
चरण IV : BC की लंबाई मापने पर, हम पाते हैं कि 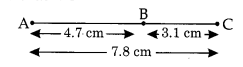
प्रश्न 4.
3.9 सेमी लंबाई की एक रेखा ![]()
(संकेत:
समाधान:
चरण I: उपयुक्त लंबाई की एक रेखा l खींचें।
चरण II:
चरण III: रेखा से,
चरण IV: फिर से
सत्यापन: 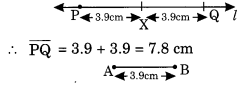
इस प्रकार
प्रश्न 5.
7.3 सेमी लंबाई वाली
हल:
चरण I: 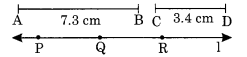
चरण II: दी गई रेखा l पर एक बिंदु P लें।
चरण III:
चरण IV:
सत्यापन: मापने पर, हम देखते हैं कि
=
इस प्रकार,
Ex 14.3
प्रश्न 1.
कोई भी रेखाखंड
हल:
चरण I: अज्ञात लंबाई की
चरण II: एक रेखा l खींचिए और उस पर एक बिंदु A अंकित कीजिए।
चरण III: कम्पास को PQ के बराबर खोलिए।
चरण IV: कम्पास की सुई को A पर रखें और l पर एक बिंदु B अंकित कीजिए।
इस प्रकार, 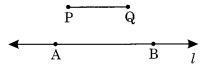
प्रश्न 2.
कुछ रेखाखंड
हल:
चरण I: किसी भी उपयुक्त लंबाई की
चरण II : कम्पास की सुई को A पर और पेंसिल के दूसरे सिरे को B पर रखें।
चरण III : एक रेखा l खींचें और उस पर एक बिंदु P लें।
चरण IV : कम्पास के उसी छेद से सुई को P पर रखें और l पर एक और बिंदु Q अंकित करें।
इस प्रकार 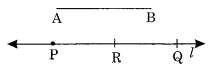
Ex 14.4
प्रश्न 1.
कोई भी रेखाखंड \(\overline { AB }\) खींचिए। इस पर कोई बिंदु M बनाइए। M से होकर \(\overline { AB }\) पर लंब खींचिए। (रूलर और परकार का प्रयोग कीजिए) हल: चरण I : एक रेखाखंड \(\overline { AB }\) खींचिए और इस पर कोई भी बिंदु M अंकित कीजिए। चरण II : परकार की नोक को M पर रखिए और उपयुक्त त्रिज्या का एक चाप इस प्रकार खींचिए कि वह \(\overline { AB }\) को P और Q पर प्रतिच्छेद करे। चरण III : P और Q को केंद्र मानकर और PM से अधिक त्रिज्या लेकर, दो चाप इस प्रकार खींचिए कि वे एक दूसरे को C पर प्रतिच्छेद करें। चरण IV : M और C को मिलाइए। अतः CM, \(\overline { AB }\) पर लंब है।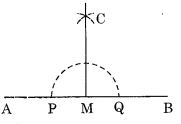
प्रश्न 2.
कोई भी रेखाखंड \(\overline { PQ }\) खींचिए। कोई भी बिंदु R लीजिए जो इस पर न हो। R से होकर \(\overline { PQ }\) पर एक लंब खींचिए। (रूलर और सेट स्क्वायर का प्रयोग कीजिए)। हल: चरण I: एक रेखाखंड \(\overline { PQ }\) और \(\overline { PQ }\) के बाहर एक बिंदु R खींचिए। चरण II: \(\overline { PQ }\) पर एक सेट स्क्वायर इस प्रकार रखिए कि इसके समकोण की एक भुजा इसके अनुदिश हो। चरण III: सेट स्क्वायर की लंबी भुजा के अनुदिश एक रूलर रखिए। चरण IV: रूलर को स्थिर पकड़िए और सेट स्क्वायर को रूलर के अनुदिश तब तक सरकाइए जब तक वह बिंदु R को न छू ले। चरण V: R से होकर जाने वाले किनारे के अनुदिश RM को मिलाइए। इस प्रकार \(\overline { RM }\) ⊥ \(\overline { PQ }\)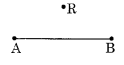
प्रश्न 3.
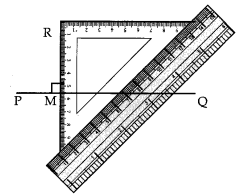
एक रेखा l और उस पर एक बिंदु X खींचिए। X से होकर l पर लंबवत एक रेखाखंड \(\overline { XY }\) खींचिए। अब \(\overline { XY }\) पर y पर लंबवत खींचिए। (रूलर और परकार का प्रयोग कीजिए) हल: चरण I: एक रेखा l खींचिए और उस पर एक बिंदु X लीजिए। चरण II: केंद्र X लेकर और उपयुक्त त्रिज्या का एक चाप खींचिए जो रेखा l को दो बिंदुओं P और Q पर प्रतिच्छेद करे। चरण III: P और Q को केंद्र मानकर और P से अधिक त्रिज्या लेकर दो चाप खींचिए जो एक दूसरे को M पर प्रतिच्छेद करें। चरण IV: XM को मिलाइए और Y तक बढ़ाइए। चरण V: Y को केंद्र मानकर और एक उपयुक्त त्रिज्या लेकर, XY को दो बिंदुओं R और S पर प्रतिच्छेद करने के लिए एक चाप खींचिए। चरण VI: R और S को केंद्र मानकर और YR से अधिक त्रिज्या लेकर, दो चाप खींचिए जो एक दूसरे को A पर प्रतिच्छेद करें। चरण VII: Y और A को मिलाइए। इस प्रकार YA ⊥ XY।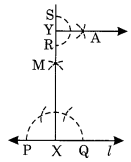
Ex 14.5
प्रश्न 1.
7.3 सेमी लंबाई का एक रेखाखंड AB खींचिए और इसकी सममिति अक्ष ज्ञात कीजिए।
हल:
चरण I: \(\overline { AB }\) = 7.3 सेमी खींचिए। चरण II: A और B को केंद्र मानकर और \(\overline { AB }\) के आधे से अधिक त्रिज्या लेकर, दो चाप खींचिए जो एक दूसरे को C और D पर प्रतिच्छेद करते हैं। चरण III: C और D को मिलाकर \(\overline { AB }\) को E पर प्रतिच्छेद कीजिए। इस प्रकार, CD \(\overline { AB }\) का लंब समद्विभाजक या सममिति अक्ष है।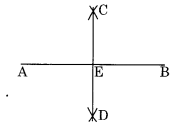
प्रश्न 2.
9.5 cm लंबाई का एक रेखाखंड खींचिए और उसका लंब समद्विभाजक खींचिए।
हल:
चरण I: 9.5 cm लंबाई का एक रेखाखंड \(\overline { PQ }\) खींचिए। चरण II: P और Q को केंद्र मानकर तथा PQ के आधे से अधिक त्रिज्या लेकर दो चाप खींचिए जो R और S पर एक दूसरे से मिलते हैं। चरण III: R और S को मिलाकर \(\overline { PQ }\) को T पर मिलाइए। इस प्रकार, RS, PQ का लंब समद्विभाजक है।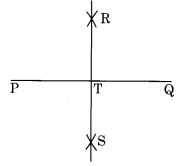
प्रश्न 3.
\(\overline { XY }\) का लंब समद्विभाजक खींचिए जिसकी लंबाई 10.3 सेमी है। (a) खींचे गए समद्विभाजक पर कोई बिंदु P लीजिए। जाँच कीजिए कि क्या PX = PY है। (b) यदि M \(\overline { XY }\) का मध्यबिंदु है। आप MX और MY की लंबाई के बारे में क्या कह सकते हैं? हल: चरण I: एक रेखाखंड \(\overline { XY }\) = 10.3 सेमी खींचिए। चरण II: केंद्र X और Y तथा XY के आधे से अधिक त्रिज्या लेकर दो चाप खींचिए जो एक दूसरे को U और V पर मिलते हैं। चरण III: U और V को मिलाइए जो \(\overline { XY }\) को M पर मिलते हैं। चरण IV: \(\overline { UV }\) पर एक बिंदु P लीजिए। (a) मापने पर, PX = PY = 5.6 सेमी। (b) मापने पर, \(\overline { MX }\) = \(\overline { MY }\) = \(\frac { 1 }{ 2 }\) XY = 5.15 सेमी.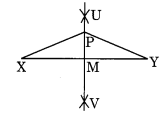
प्रश्न 4.
12.8 सेमी लंबाई का एक रेखाखंड खींचें। परकार का उपयोग करके इसे चार बराबर भागों में विभाजित करें। वास्तविक माप से सत्यापित करें।
हल:
चरण I: 12.8 सेमी लंबाई का एक रेखाखंड \(\overline { AB }\) खींचें। चरण II: केंद्र A और B लेकर और AB के आधे से अधिक त्रिज्या लेकर दो चाप लगाएं जो एक दूसरे को D और E पर मिलते हैं। चरण III: D और E को मिलाएं जो \(\overline { AB }\) को C पर मिलते हैं जो \(\overline { AB }\) का मध्यबिंदु है। चरण IV: केंद्र A और C लेकर और AC के आधे से अधिक त्रिज्या लेकर दो चाप लगाएं जो एक दूसरे को F और G पर मिलते हैं। चरण V: F और G को मिलाएं जो \(\overline { AC }\) को H पर मिलते हैं जो \(\overline { AC }\) का मध्यबिंदु है। चरण VI : C और B को केंद्र मानकर तथा CB के आधे से अधिक त्रिज्या लेकर, दो चाप खींचिए जो J और K पर एक दूसरे से मिलते हैं। चरण VII : J और K को मिलाइए जो \(\overline { CB }\) को L पर मिलते हैं जो \(\overline { CB }\) का मध्यबिंदु है। इस प्रकार, मापने पर, हम पाते हैं \(\overline { AH }\) = \(\overline { HC }\) = \(\overline { CL }\) = \(\overline { LB }\) = 3.2 सेमी।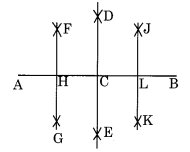
प्रश्न 5.
6.1 cm लंबाई वाली \(\overline { PQ }\) को व्यास मानकर एक वृत्त खींचिए। हल: चरण I: \(\overline { PQ }\) = 6.1 cm खींचिए। चरण II: \(\overline { PQ }\) का एक लंब समद्विभाजक खींचिए जो \(\overline { PQ }\) को R पर मिलता है अर्थात R, \(\overline { PQ }\) का मध्यबिंदु है। चरण III: केंद्र R और त्रिज्या \(\overline { RP }\) के बराबर लेकर, P और Q से होकर गुजरने वाला एक वृत्त खींचिए। इस प्रकार, \(\overline { PQ }\) = 6.1 cm व्यास वाला वृत्त अभीष्ट वृत्त है।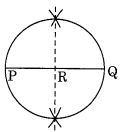
प्रश्न 6.
केंद्र C और त्रिज्या 3.4 सेमी लेकर एक वृत्त खींचिए। कोई भी जीवा \(\overline { AB }\) खींचिए। \(\overline { AB }\) का लंब समद्विभाजक खींचिए और जाँचिए कि क्या यह C से होकर जाता है। हल: चरण I: केंद्र C और त्रिज्या 3.4 सेमी लेकर एक वृत्त खींचिए। चरण II: कोई भी जीवा \(\overline { AB }\) खींचिए। चरण III: \(\overline { AB }\) का लंब समद्विभाजक खींचिए जो केंद्र C से होकर जाता है।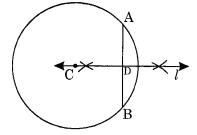
प्रश्न 7.
यदि \(\overline { AB }\) एक व्यास है, तो प्रश्न संख्या 6 दोहराएँ। हल: चरण I: केंद्र C और त्रिज्या 3.4 सेमी लेकर एक वृत्त खींचिए। चरण II: वृत्त का व्यास AB खींचिए। चरण III: AB का एक लंब समद्विभाजक खींचिए जो केंद्र C से होकर जाता है और मापने पर, हम पाते हैं कि C, \(\overline { AB }\) का मध्यबिंदु है।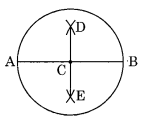
प्रश्न 8.
4 सेमी त्रिज्या वाला एक वृत्त खींचिए। इसकी कोई दो जीवाएँ खींचिए। इन जीवाओं के लंब समद्विभाजक बनाइए। ये कहाँ मिलती हैं?
हल:
चरण I: केंद्र 0 और त्रिज्या 4 सेमी लेकर एक वृत्त खींचिए।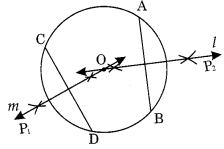
चरण II: वृत्त की कोई दो जीवाएँ \(\overline { AB }\) और \(\overline { CD }\) खींचिए। चरण III: \(\overline { AB }\) और \(\overline { CD }\) के लंब समद्विभाजक अर्थात् I और m खींचिए। चरण IV: बढ़ाने पर दोनों लंब समद्विभाजक वृत्त के केंद्र O पर एक दूसरे से मिलते हैं।
प्रश्न 9.
शीर्ष O वाला कोई कोण खींचिए। इसकी एक भुजा पर बिंदु A और दूसरी भुजा पर बिंदु B इस प्रकार लीजिए कि OA = OB। \(\overline { OA }\) और \(\overline { OB }\) के लंब समद्विभाजक खींचिए। उन्हें P पर मिलने दीजिए। क्या PA = PB है? हल: चरण I: शीर्ष O लेकर कोण XOY खींचिए। चरण II: OY पर कोई बिंदु A और OX पर कोई बिंदु B इस प्रकार लीजिए कि OA + OB। चरण III: OA और OB के लंब समद्विभाजक खींचिए जो एक दूसरे से बिंदु P पर मिलते हैं। चरण IV: \(\overline { PA }\) और \(\overline { PB }\) की लंबाई मापें। हाँ, \(\overline { PA }\) = \(\overline { PB }\)।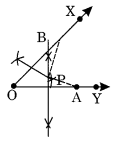
Ex 14.6
प्रश्न 1.
75° माप का ∠POQ खींचिए और इसकी सममित रेखा ज्ञात कीजिए।
हल:
चरण I: एक रेखाखंड \(\overline { PQ }\) खींचिए। चरण II: केंद्र Q और उपयुक्त त्रिज्या लेकर, PQ को R पर काटने के लिए एक चाप लगाइए। चरण III: केंद्र R और समान लंबाई की त्रिज्या लेकर, पहले चाप पर S और T अंकित कीजिए। चरण IV: केंद्रों S और T तथा समान त्रिज्या लेकर, दो चाप खींचिए जो एक दूसरे को U पर मिलते हैं। चरण V: QU को इस प्रकार मिलाइए कि ∠PQU = 90° हो। चरण VI: केंद्रों S और W लेकर, समान त्रिज्या के दो चाप खींचिए जो एक दूसरे को Q पर मिलते हैं। चरण VII: Q और O को इस प्रकार मिलाइए कि ∠PQO = 75° हो। चरण VIII: ∠PQO को QV से समद्विभाजित कीजिए। इस प्रकार, OV, ∠PQO की सममित रेखा है।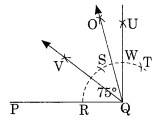
प्रश्न 2.
147° माप का एक कोण खींचिए और उसका समद्विभाजक खींचिए।
हल:
चरण I: चाँदे की सहायता से ∠ABC = 147° का कोण खींचिए।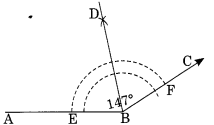
चरण II: केंद्र B और उचित लंबाई की त्रिज्या लेकर एक चाप लगाइए जो AB और AC को क्रमशः E और F पर मिले।
चरण III: केंद्र E और F लेकर तथा चाप EF की लंबाई के आधे से अधिक त्रिज्या लेकर दो चाप लगाइए जो एक दूसरे को D पर मिलते हैं।
चरण IV: B और D को मिलाइए।
इस प्रकार, BD, ∠ABC का समद्विभाजक है।
प्रश्न 3.
एक समकोण खींचिए और उसका समद्विभाजक खींचिए।
हल:
चरण I: एक रेखाखंड AB खींचिए।
चरण II: केंद्र B और उचित त्रिज्या लेकर एक चाप खींचिए जो AB को C पर मिले।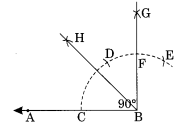
चरण III: केंद्र C और समान त्रिज्या लेकर पहले वाले चाप पर दो चिह्न D और E अंकित कीजिए।
चरण IV: केंद्र D और E तथा समान त्रिज्या लेकर दो चाप खींचिए जो एक दूसरे को G पर मिलते हैं।
चरण V: B और G को इस प्रकार मिलाइए कि ∠ABG = 90°
चरण VI: ∠ABG का समद्विभाजक BH इस प्रकार खींचिए कि ∠ABH = 45° हो।
इस प्रकार ∠ABG समकोण है और BH, ∠ABG का समद्विभाजक है।
प्रश्न 4.
153° का एक कोण खींचिए और उसे चार बराबर भागों में विभाजित कीजिए।
हल:
चरण I: चाँदे की सहायता से ∠ABP = 153° का कोण खींचिए।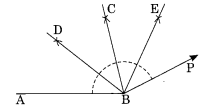
चरण II: ∠ABP का समद्विभाजक BC खींचिए जो ∠ABP को दो बराबर भागों में विभाजित करता है।
चरण III: ∠ABC और ∠CBP के समद्विभाजक क्रमशः BD और BE खींचिए। इस प्रकार, समद्विभाजक BD, BC और BE, ∠ABP को चार बराबर भागों में विभाजित करते हैं।
प्रश्न 5.
रूलर और परकार की सहायता से निम्नलिखित मापों के कोण बनाइए:
(a) 60°
(b) 30°
(c) 90°
(d) 120°
(e) 45°
(f) 135°
हल:
(a) 60° का कोण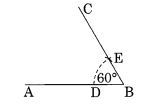
चरण I: एक रेखाखंड \(\overline { AB }\) खींचिए। चरण II: केंद्र B और उचित त्रिज्या लेकर एक चाप खींचिए। चरण III: केंद्र D और समान लंबाई की त्रिज्या लेकर पहले चाप पर एक बिंदु E अंकित कीजिए। चरण IV: B को E से मिलाइए और C से गुणनफल कीजिए। इस प्रकार ∠ABC 60° माप का अभीष्ट कोण है।
(b) चरण I: ∠ABC = 60° बनाएँ जैसा कि हमने भाग (a) में किया है।
चरण II: ∠ABC का समद्विभाजक BF बनाएँ।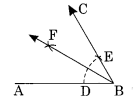
इस प्रकार ∠ABF = \(\frac { 60 }{ 2 }\) = 30°।
(c) 90° का कोण
दी गई आकृति में,
∠ABC = 90° (हल 3 देखें)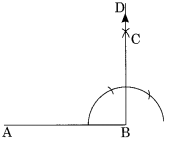
(d) 120° का कोण।
चरण I: \(\overline { AB }\) खींचिए। चरण II: केंद्र A और उचित लंबाई की त्रिज्या लेकर एक चाप लगाइए। चरण III: केंद्र D और समान त्रिज्या लेकर पहले चाप पर दो चिह्न E और F खींचिए। चरण IV: A को F से मिलाइए और C तक बढ़ाइए। इस प्रकार ∠CAB = 120°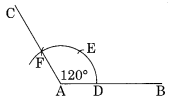
(e) 45° का कोण, अर्थात् \(\frac { 90 }{ 2 }\) = 45° आकृति में ∠ABD = 45° (हल 3 देखें)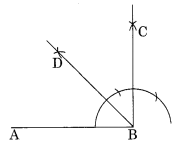
(f) 135° का कोण
चूँकि 135° = 90° + 45°
= 90° + (\(\frac { 90 }{ 2 }\) )° इस आकृति में ∠ABC = 135°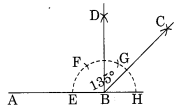
प्रश्न 6.
45° का एक कोण खींचिए और उसे समद्विभाजित कीजिए।
हल:
चरण I: एक रेखा AB खींचिए और उस पर कोई बिंदु O लीजिए।
चरण II: O पर ∠AOE = 45° का कोण बनाइए।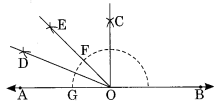
चरण III: केंद्र O और उचित त्रिज्या लेकर, एक चाप GF खींचिए।
चरण IV: केंद्र G और F लेकर और उचित त्रिज्या लेकर, दो चाप खींचिए जो एक दूसरे को D पर काटते हैं।
चरण V: O को D से मिलाइए।
इस प्रकार ∠AOE = 45° और OD इसका समद्विभाजक है।
प्रश्न 7.
135° का एक कोण खींचिए और उसे समद्विभाजित कीजिए।
हल:
चरण I: एक रेखा OA खींचिए और उस पर कोई बिंदु P लीजिए।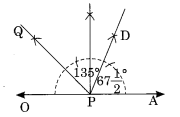
चरण II: ∠APQ = 135° की रचना कीजिए।
चरण III: PD को कोण APQ का समद्विभाजक बनाइए।
इस प्रकार ∠APQ = \(\frac { { 135 }^{ } }{ 2 }\) = 67 \(\frac { { 1 }^{ } }{ 2 }\).
प्रश्न 8.
70° का कोण बनाएं। केवल एक सीधी धार और परकार का उपयोग करके इसकी प्रतिलिपि बनाएं।
हल:
चरण I: एक रेखा AB खींचें और उस पर कोई बिंदु 0 लें।
चरण II: चाँदे का उपयोग करके ∠COB = 70° बनाएं।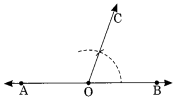
चरण III: एक किरण \(\overrightarrow { PQ }\) बनाएं। चरण IV: केंद्र O और उचित त्रिज्या लेकर, एक चाप लगाएं जो क्रमशः \(\overrightarrow { OA }\) और \(\overrightarrow { OB }\) को E और F पर मिलता है। चरण V: समान त्रिज्या और केंद्र P लेकर, \(\overrightarrow { PQ }\) को R पर मिलते हुए एक चाप लगाएं। चरण VI: केंद्र R लेकर और त्रिज्या EF के बराबर रखते हुए, पहले चाप को S पर काटते हुए एक चाप लगाएं। चरण VII: P और S को मिलाएं और इसे आगे बढ़ाएं। इस प्रकार, QPS, AOB = 70° का प्रतिलिपि है।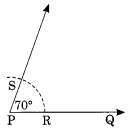
प्रश्न 9.
40° का एक कोण बनाएं। इसके संपूरक कोण की प्रतिलिपि बनाएँ।
हल:
चरण I: चाँदे की सहायता से ∠AOB = 40° की रचना करें।
∠COF, ∠AOB का संपूरक कोण है।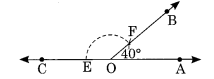
चरण II: एक किरण \(\overrightarrow { PR }\) खींचें और उस पर कोई बिंदु Q लें। चरण III: केंद्र O और उचित त्रिज्या लेकर, एक चाप लगाएं जो \(\overrightarrow { OC }\) और \(\overrightarrow { OB }\) को क्रमशः E और F पर प्रतिच्छेद करता है। चरण IV: केंद्र Q और समान त्रिज्या लेकर, एक चाप लगाएं जो \(\overrightarrow { PQ }\) को L पर प्रतिच्छेद करता है। चरण V: केंद्र L और त्रिज्या EF के बराबर लेकर, एक चाप लगाएं जो पहले चाप को S पर प्रतिच्छेद करता है। चरण VI: Q और S को मिलाएं और बढ़ाया। इस प्रकार, ∠PQS, संपूरक कोण COB का प्रतिरूप है।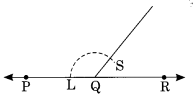
InText Questions
अति लघु उत्तरीय प्रश्न
प्रश्न 1.
यदि AB = 3.6 और CD = 1.6 सेमी, तो \(\overline { AB }\) + \(\overline { CD }\) के बराबर एक रेखाखंड की रचना कीजिए और कुल लंबाई मापिए। हल: चरण I: एक किरण OX खींचिए। चरण II: केंद्र 0 और त्रिज्या AB (3.6 सेमी) के बराबर लेकर किरण पर एक बिंदु P अंकित कीजिए। चरण III: केंद्र P और त्रिज्या CD (1.6 सेमी) के बराबर लेकर किरण पर एक और बिंदु Q अंकित कीजिए। इस प्रकार OQ अभीष्ट रेखाखंड है जिससे OQ = 3.6 सेमी + 1.6 सेमी = 5.2 सेमी है।
![]()
प्रश्न 2.
किसी दिए गए रेखाखंड पर एक बिंदु पर लंब की रचना कीजिए।
हल:
चरण I: एक रेखा \(\overleftrightarrow { PQ }\) खींचिए और उस पर कोई बिंदु A लीजिए। चरण II: केंद्र A लेकर एक चाप लगाइए जो PQ को C और D पर मिले। चरण III: AB को मिलाइए और बढ़ाइए। चरण IV: केंद्र C और D लेकर तथा पिछली चाप की लंबाई के आधे के बराबर त्रिज्या लेकर, दो चाप लगाइए जो एक दूसरे को B पर मिलें। इस प्रकार AB, \(\overleftrightarrow { PQ }\) पर अभीष्ट लंब है।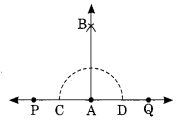
प्रश्न 3.
60° का कोण बनाएँ और उसे समद्विभाजित करें।
हल:
चरण I: एक रेखाखंड \(\overline { AB }\) खींचिए। चरण II: केंद्र B और उचित त्रिज्या लेकर एक चाप लगाइए जो AB को C पर मिले। चरण III: C को केंद्र मानकर और चरण II के समान त्रिज्या लेकर एक चाप लगाइए जो पिछले चाप को D पर काटता है। चरण IV: B को D से मिलाइए और बढ़ाइए। चरण V: ∠ABD का समद्विभाजक BE खींचिए। इस प्रकार BE, ∠ABD का अभीष्ट समद्विभाजक है।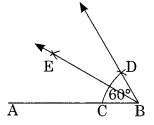
प्रश्न 4.
120° का कोण बनाएं और इस प्रकार 105° का कोण बनाएं।
हल:
चरण I: एक रेखाखंड \(\overline { OA }\) खींचें। चरण II: केंद्र O और उचित त्रिज्या लेकर, एक चाप लगाएं जो OA को C पर मिले। चरण III: केंद्र C और समान त्रिज्या लेकर, पिछले चाप पर D और E अंकित करें। चरण IV: O को E से मिलाएं और बढ़ाएं। चरण V: ∠EOA 120° का अभीष्ट कोण है। चरण VI: 90° का कोण बनाएं जो पिछले चाप को F पर मिलता है। चरण VII: केंद्र E और F तथा उचित त्रिज्या लेकर, दो चाप लगाएं जो एक दूसरे को G पर मिलते हैं। चरण VIII: OG को मिलाएं और बढ़ाएं। इस प्रकार ∠GOA 105° का अभीष्ट कोण है।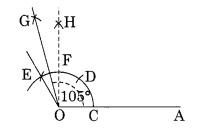
परकार और रूलर का उपयोग करके 75°
का कोण बनाएं और इस प्रकार 37 ![]()
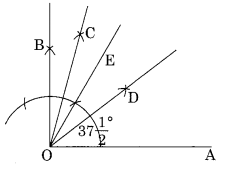
प्रश्न 6.
∆ABC खींचिए। A, B और C से क्रमशः भुजाओं BC, CA और AB पर लंब खींचिए। क्या ये लंब एक ही बिंदु से होकर जाते हुए संगामी हैं?
हल:
चरण I: कोई भी ∆ABC खींचिए।
चरण II: A से BC पर लंब AD खींचिए।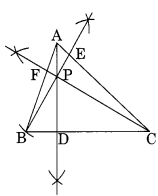
चरण III: B से AC पर लंब BE खींचिए।
चरण IV: C से AB पर लंब CF खींचिए।
हम देखते हैं कि लंब AD, BE और CF एक दूसरे को P पर काटते हैं।
इस प्रकार, P तीनों लंबों का प्रतिच्छेद बिंदु है।
