SikhLo - Current Affairs in Hindi, Daily current affairs, Current affairs

NCERT कक्षा 6 गणित अध्याय 3 संख्याओं के साथ खेलना

Ex 3.1

प्रश्न 1.
निम्नलिखित संख्याओं के सभी गुणनखंड लिखिए:
(a) 24 (b) 15 (c) 21
(d) 27 (e) 12 (f) 20
(g) 18 (h) 23 (i) 36
हल:
(a) 24 के गुणनखंड हैं:
24 = 1 x 24;
24 = 2 x 12;
24 = 3 x 8;
24 = 4 x 6
अतः, 24 के सभी गुणनखंड हैं: 1, 2, 3, 4, 6, 8, 12 और 24।

(b) 15 के गुणनखंड हैं:
15 = 1 x 15;
15 = 3 x 5
अतः, 15 के सभी गुणनखंड हैं: 1, 3, 5 और 15.

(c) 21 के गुणनखंड हैं:
21 = 1 x 21;
21 = 3 x 7
अतः, 21 के सभी गुणनखंड हैं: 1, 3, 7 और 21.

(d) 27 के गुणनखंड हैं:
27 = 1 x 27;
27 = 3 x 9.
अतः, 27 के सभी गुणनखंड हैं: 1, 3, 9 और 27.

(e) 12 के गुणनखंड हैं:
12 = 1 x 12;
12 = 2 x 6;
12 = 3 x 4
अतः, 12 के सभी गुणनखंड हैं: 1, 2, 3, 4, 6 और 12.

(च) 20 के गुणनखंड हैं:
20 = 1 x 20;
20 = 2 x 10;
20 = 4 x 5
अतः, 20 के सभी गुणनखंड हैं: 1, 2, 4, 5, 10 और 20.

(g) 18 के गुणनखंड हैं:
18 = 1 x 18;
18 = 2 x 9;
18 = 3 x 6
अतः, 18 के सभी गुणनखंड हैं: 1, 2, 3, 6, 9 और 18.

(h) 23 के गुणनखंड हैं:
23 = 1 x 23
अतः, अभाज्य संख्या 23 के सभी गुणनखंड हैं: 1 और 23.

(i) 36 के गुणनखंड हैं:
36 = 1 x 36;
36 = 2 x 18;
36 = 3 x 12;
36 = 4 x 9;
36 = 6 x 6
अतः, 36 के सभी गुणनखंड हैं: 1, 2, 3, 4, 6, 9, 12, 18 और 36.

प्रश्न 2.
इनके प्रथम पाँच गुणज लिखिए:
(a) 5 (b) 8 (c) 9
हल:
(a) 5 के प्रथम पाँच गुणज हैं:
5 x 1 = 5;
5 x 2 = 10;
5 x 3 = 15;
5 x 4 = 20;
5 x 5 = 25
अतः, 5 के अभीष्ट गुणज हैं: 5, 10, 15, 20 और 25.

(b) 8 के प्रथम पाँच गुणज हैं:
8 x 1 = 8;
8 x 2 = 16;
8 x 3 = 24;
8×4 = 32;
8 x 5 = 40
अतः, 8 के अभीष्ट गुणज हैं: 8, 16, 24, 32 और 40.

(c) 9 के प्रथम पाँच गुणज हैं:
9 x 1 = 9;
9 x 2 = 18;
9 x 3 = 27;
9 x 4 = 36;
9 x 5 = 45
अतः, 9 के अभीष्ट गुणज हैं: 9,18, 27, 36 और 45.

प्रश्न 3.
कॉलम I के पदों को कॉलम II के पदों से सुमेलित कीजिए।

हल:
(i) ↔ (b) [∵ 7 x 5 = 35]
(ii) ↔ (d) [∵ 15 x 2 = 30]
(iii) ↔ (a) [∵ 8 x 2 = 16]
(iv) ↔ (f) [∵ 20 x 1 = 20]
(v) ↔ (e) [∵ 25 x 2 = 50]

प्रश्न 4.
100 तक 9 के सभी गुणज ज्ञात कीजिए।
हल:
9 x 1 = 9;
9 x 2 = 18;
9 x 3 = 27;
9 x 4 = 36; 9
x 5 = 45;
9 x 6 = 54;
9 x 7 = 63;
9 x 8 = 72;
9 x 9 = 81;
9 x 10 = 90;
9 x 11 = 99
अतः, 100 तक 9 के सभी गुणज हैं:
9, 18, 27, 36, 45, 54, 63, 72, 81, 90 और 99।

Ex 3.2

प्रश्न 1.
किन्हीं दो का योग क्या है:
(a) विषम संख्याएँ?
(b) सम संख्याएँ?
हल:
(a) किन्हीं दो विषम संख्याओं का योग सम होता है।
(b) किन्हीं दो सम संख्याओं का योग सम होता है।

प्रश्न 2.
बताइए कि निम्नलिखित कथन सत्य हैं या असत्य।
(a) तीन विषम संख्याओं का योग सम होता है।
(b) दो विषम संख्याओं और एक सम संख्या का योग सम होता है।
(c) तीन विषम संख्याओं का गुणनफल विषम होता है।
(d) यदि एक सम संख्या को 2 से विभाजित किया जाता है, तो भागफल सदैव विषम होता है।
(e) सभी अभाज्य संख्याएँ विषम होती हैं।
(f) अभाज्य संख्याओं का कोई गुणनखंड नहीं होता है।
(g) दो अभाज्य संख्याओं का योग सदैव सम होता है।
(h) 2 केवल सम अभाज्य संख्या है।
(i) सभी सम संख्याएँ भाज्य संख्याएँ होती हैं।
(j) किन्हीं दो सम संख्याओं का गुणनफल सदैव सम होता है।
हल:
(a) असत्य [∵ 3 + 5 + 7 = 15 (विषम)]
(b) सत्य [∵ 3 + 5 + 6 = 14 (सम)]
(c) सत्य [∵ 5 x 7 x 9 = 315 (विषम)]
(d) असत्य [∵ 6 + 2 = 3 (विषम)]
(e) असत्य [∵ 2 एक अभाज्य संख्या है लेकिन यह सम है]
(f) असत्य [∵ 3 एक अभाज्य संख्या है जिसके गुणनखंड 1 और 3 हैं]
(g) असत्य [∵ 7 + 2 = 9 (विषम)]
(h) सत्य [∵ 2 सम है और सबसे छोटी अभाज्य संख्या है]
(i) असत्य [∵ 2 सम है लेकिन भाज्य संख्या नहीं है]
(j) सत्य [∵ 4 x 6 = 24 (सम)]

प्रश्न 3.
संख्याएँ 13 और 31 अभाज्य संख्याएँ हैं। इन दोनों संख्याओं के अंक 1 और 3 समान हैं। 100 तक अभाज्य संख्याओं के ऐसे युग्म ज्ञात कीजिए।
हल:
समान अंकों वाले अभाज्य संख्याओं के अभीष्ट युग्म हैं:
(17 और 71), (37 और 73), (79 और 97)।

प्रश्न 4.
20 से छोटी अभाज्य और भाज्य संख्याएँ अलग-अलग लिखिए।
हल:
20 से छोटी अभाज्य संख्याएँ हैं:
2, 3, 5, 7, 11, 13, 17 और 19
20 से छोटी भाज्य संख्याएँ हैं:
4, 6, 8, 9, 10, 12, 14, 15, 16 और 18

 प्रश्न 5.
1 और 10 के बीच सबसे बड़ी अभाज्य संख्या क्या है?
हल:
1 और 10 के बीच सबसे बड़ी अभाज्य संख्या 7 है।

प्रश्न 6.
निम्नलिखित को दो विषम अभाज्य संख्याओं के योग के रूप में व्यक्त करें।
(a) 44
(b) 36
(c) 24
(d) 18
हल:
(a) 44 = 13 + 31
(b) 36 = 17 + 19
(c) 24 = 7 + 17
(d) 18 = 7 + 11

प्रश्न 7.
अभाज्य संख्याओं के तीन युग्म दीजिए जिनका अंतर 2 है।
[टिप्पणी: दो अभाज्य संख्याएँ जिनका अंतर 2 है, अभाज्य जुड़वाँ कहलाती हैं]
हल:
आवश्यक युग्म हैं: (3 और 5), (5 और 7) तथा (11 और 13)

प्रश्न 8.
निम्नलिखित में से कौन सी संख्याएँ अभाज्य हैं?
(a) 23
(b) 51
(c) 37
(d) 26
हल:
(a) 23 एक अभाज्य संख्या है [∵ 23 = 1 x 23]
(b) 51 एक अभाज्य संख्या नहीं है [∵ 51 = 1 x 3 x 17]
(c) 37 एक अभाज्य संख्या है [∵ 37 = 1 x 37]
(d) 26 एक अभाज्य संख्या नहीं है [∵ 26 = 1 x 2 x 13]

प्रश्न 9.
100 से छोटी सात क्रमागत भाज्य संख्याएँ लिखिए ताकि उनके बीच कोई अभाज्य संख्या न हो।
हल:
आवश्यक सात क्रमागत भाज्य संख्याएँ हैं:
90, 91, 92, 93, 94, 95 और 96

प्रश्न 10.
निम्नलिखित संख्याओं में से प्रत्येक को तीन विषम अभाज्य संख्याओं के योग के रूप में व्यक्त करें।
(a) 21
(b) 31
(c) 53
(d) 61
हल:
(a) 21 को 3 + 5 + 13 के रूप में व्यक्त किया जा सकता है
(b) 31 को 5 + 7 + 19 के रूप में व्यक्त किया जा सकता है
(c) 53 को 13 + 17 + 23 के रूप में व्यक्त किया जा सकता है
(d) 61 को 11 + 13 + 37 के रूप में व्यक्त किया जा सकता है

प्रश्न 11.
20 से छोटी अभाज्य संख्याओं के पाँच युग्म लिखिए जिनका योग 5 से विभाज्य हो।
(संकेत: 3 + 7 = 10)
हल:
20 से छोटी अभाज्य संख्याओं के अभीष्ट युग्म हैं:
(i) 2 + 3 = 5
(ii) 2 + 13 = 15
(iii) 11 + 9 = 20
(iv) 17 + 3 = 20
(v) 7 + 13 = 20

प्रश्न 12.
रिक्त स्थान भरें।
(a) वह संख्या जिसके केवल दो गुणनखंड हों, ………… कहलाती है।
(b) वह संख्या जिसके दो से अधिक गुणनखंड हों, ………… कहलाती है।
(c) 1 न तो ………… है और न ही ………… है।
(d) सबसे छोटी अभाज्य संख्या ………… है।
(e) सबसे छोटी भाज्य संख्या ………… है।
(f) सबसे छोटी सम संख्या ………… है।
हल:
(a) अभाज्य संख्या
(b) भाज्य संख्या
(c) अभाज्य, भाज्य
(d) 2
(e) 4
(f) 2

Ex 3.3

प्रश्न 1.
विभाज्यता परीक्षणों का उपयोग करके, निर्धारित करें कि निम्नलिखित में से कौन सी संख्याएँ 2 से, 3 से, 4 से, 5 से, 6 से, 8 से, 9 से, 10 से, 11 से विभाज्य हैं (हाँ या नहीं कहें)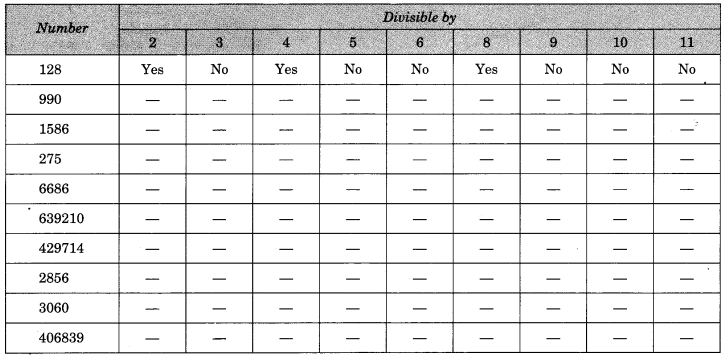

हल: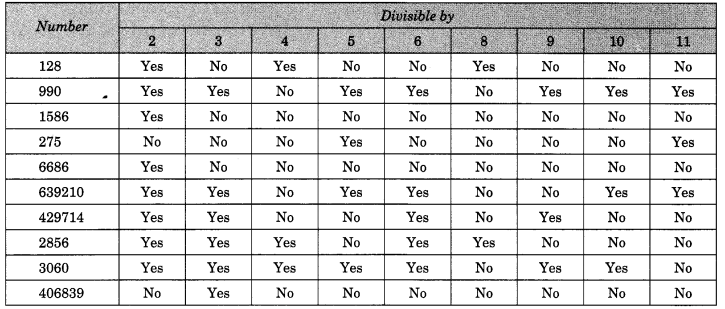

प्रश्न 2.
विभाज्यता परीक्षणों का उपयोग करके, निर्धारित करें कि निम्नलिखित में से कौन सी संख्याएँ 4 से विभाज्य हैं; 8 से।
(a) 572
(b) 726352
(c) 5500 (
d) 6000 (e) 12159 (f) 14560 (g) 21084 (j) 2150 (h) 31795072 (i) 1700 हल: (a) दी गई संख्या = 572 (i) 4 से विभाज्यता यहाँ, दी गई संख्या के अंतिम दो अंकों द्वारा गठित संख्या 72 है। शेष 0। इसलिए, 572 4 से विभाज्य है।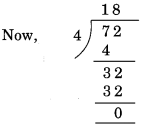

(ii) 8 से विभाज्यता
यहाँ, दी गई संख्या के अंतिम तीन अंकों से बनी संख्या 572 है।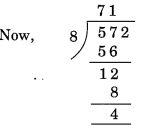

शेष 4 है। अतः 572, 8 से विभाज्य नहीं है।

(b) दी गई संख्या = 726352
(i) 4 से विभाज्यता
यहाँ, दी गई संख्या के अंतिम दो अंकों से बनी संख्या = 52.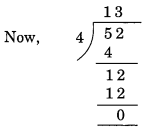

शेष = 0.
अतः 726352, 4 से विभाज्य है।

(ii) 8 से विभाज्यता
यहाँ, दी गई संख्या के अंतिम तीन अंकों से बनी संख्या = 352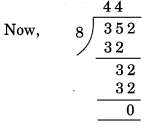

शेष = 0.
अतः, 726352 से विभाज्य है।

(c) दी गई संख्या = 5500
(i) 4 से विभाज्यता
यहाँ दी गई संख्या के अंतिम दो अंक 0 हैं। अतः 5500, 4 से विभाज्य है।
(ii) 8 से विभाज्यता
यहाँ, दी गई संख्या के अंतिम तीन अंकों से बनी संख्या = 500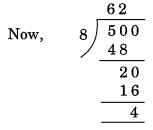

शेष = 4. अतः 5500, 8 से विभाज्य नहीं है।

(d) दी गई संख्या = 6000
(i) 4 से विभाज्यता
यहाँ, दी गई संख्या के अंतिम दो अंक 0 हैं।
अतः 6000, 4 से विभाज्य है।

(ii) 8 से विभाज्यता
यहाँ, दी गई संख्या के अंतिम तीन अंक 0 हैं।
अतः 6000, 8 से विभाज्य है।

(e) दी गई संख्या = 12159
(i) 4 से विभाज्यता
यहाँ, दी गई संख्या के अंतिम दो अंकों से बनी संख्या = 59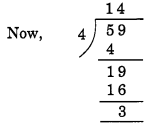

शेष = 3.
अतः 12159, 4 से विभाज्य है।

(ii) 8 से विभाज्यता
यहाँ, दी गई संख्या के अंतिम तीन अंकों से बनी संख्या = 159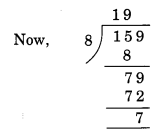

शेष = 7.
अतः 12159, 8 से विभाज्य नहीं है।

(च) दी गई संख्या = 14560
(i) 4 से विभाज्यता
यहाँ, दी गई संख्या के अंतिम दो अंकों से बनी संख्या = 60.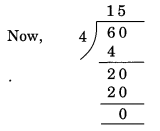

शेष = 0.
अतः 14560, 8 से विभाज्य है।

(g) दी गई संख्या = 21084
(i) 4 से विभाज्यता
यहाँ, दी गई संख्या के अंतिम दो अंकों से बनी संख्या = 84.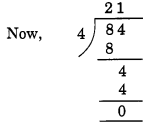

शेष = 0. अतः 21084, 4 से विभाज्य है।

(ii) 8 से विभाज्यता
यहाँ, दी गई संख्या के अंतिम तीन अंकों से बनी संख्या = 084.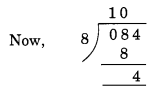

शेष = 4.
अतः 21084, 8 से विभाज्य नहीं है।

(h) दी गई संख्या = 31795072
(i) 4 से विभाज्यता
यहाँ, दी गई संख्या के अंतिम दो अंकों से बनी संख्या = 72.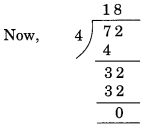

शेष = 0. अतः 31795072, 4 से विभाज्य है।

(ii) 8 से विभाज्यता
यहाँ, दी गई संख्या के अंतिम तीन अंकों से बनी संख्या = 072.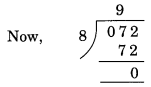

शेष = 0. अतः 31795072, 8 से विभाज्य है।

(i) दी गई संख्या = 1700
(i) 4 से विभाज्यता
यहाँ, दी गई संख्या के अंतिम दो अंक 0 हैं। अतः 1700, 4 से विभाज्य है।
(ii) 8 से विभाज्यता
यहाँ, दी गई संख्या के अंतिम तीन अंकों द्वारा गठित संख्या = 700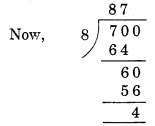

शेष = 4. अतः 1700, 8 से विभाज्य नहीं है।
(j) दी गई संख्या = 2150
(i) 4 से विभाज्यता
यहाँ, दी गई संख्या के अंतिम दो अंकों द्वारा गठित संख्या = 50.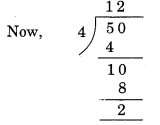

शेष = 2. अतः 2150, 4 से विभाज्य नहीं है।

(ii) 8 से विभाज्यता
यहाँ, दी गई संख्या के अंतिम तीन अंकों से बनी संख्या = 150

शेष = 6. अतः 2150, 8 से विभाज्य नहीं है।

प्रश्न 3.
विभाज्यता परीक्षणों का उपयोग करके, निर्धारित करें कि निम्नलिखित में से कौन सी संख्या 6 से विभाज्य है:
(a) 297144
(b) 1258
(c) 4335
(d) 61233
(e) 901352
(f) 438750
(g) 1790184
(h) 12583
(i) 639210
(j) 17852
हल:
हम जानते हैं कि एक संख्या 6 से विभाज्य है यदि यह 2 और 3 दोनों से भी विभाज्य है।
(a) दी गई संख्या = 297144
दी गई संख्या 297144 में इकाई के स्थान पर सम अंक है।
अतः यह 2 से विभाज्य है।
297144 के सभी अंकों का योग = 2 + 9 + 7 + 1 + 4 + 4 = 27 है
जो 3 से विभाज्य है।
अतः दी गई संख्या 297144, 6 से विभाज्य है।

(b) दी गई संख्या = 1258
दी गई संख्या 1258 का इकाई स्थान सम अंक 8 है।
अतः यह 2 से विभाज्य है।
1258 के सभी अंकों का योग = 1 + 2 + 5 + 8 = 16 है जो 3 से विभाज्य नहीं है।
अतः दी गई संख्या 1258, 6 से विभाज्य नहीं है।

(c) दी गई संख्या = 4335
दी गई संख्या का इकाई अंक सम नहीं है।
इसलिए, यह 2 से विभाज्य नहीं है।
4335 के सभी अंकों का योग = 4 + 3 + 3 + 5 = 15 जो 3 से विभाज्य है।
चूँकि दी गई संख्या 4335 2 और 3 दोनों से विभाज्य नहीं है, इसलिए यह 6 से भी विभाज्य नहीं है।

(d) दी गई संख्या = 61233
दी गई संख्या का इकाई अंक सम नहीं है।
इसलिए, यह 2 से विभाज्य नहीं है।
दी गई संख्या 61233 के अंकों का योग = 6 + 1 + 2 + 3 + 3 = 15 है जो 3 से विभाज्य है।
चूँकि दी गई संख्या 2 और 3 दोनों से विभाज्य नहीं है, इसलिए यह 6 से भी विभाज्य नहीं है।

(e) दी गई संख्या = 901352
दी गई संख्या का इकाई अंक सम है।
अतः यह 2 से विभाज्य है।
दी गई संख्या 901352 के सभी अंकों का योग = 9 + 0 + 1 + 3 + 5 + 2 = 20 है जो 3 से विभाज्य नहीं है।
चूँकि दी गई संख्या 2 और 3 दोनों से विभाज्य नहीं है, अतः यह 6 से भी विभाज्य नहीं है।

(f) दी गई संख्या = 438750
दी गई संख्या के इकाई स्थान का अंक 0 है। अतः यह 2 से विभाज्य है।
दी गई संख्या 438750 के सभी अंकों का योग
=4 + 3 + 8 + 7 + 5 + 0 = 27 है जो 3 से विभाज्य है।
अतः दी गई संख्या 6 से विभाज्य है।

(g) दी गई संख्या = 1790184
दी गई संख्या का इकाई अंक सम है।
अतः यह 2 से विभाज्य है।
दी गई संख्या 1790184 के सभी अंकों का योग
= 1 + 7 + 9 + 0 + 1 + 8 + 4 = 30 है जो 3 से विभाज्य है।
अतः दी गई संख्या 6 से विभाज्य है।

(h) दी गई संख्या = 12583
दी गई संख्या का इकाई अंक विषम है।
अतः यह 2 से विभाज्य नहीं है।
दी गई संख्या 12583 के सभी अंकों का योग
= 1 + 2 + 5 + 8 + 3 = 19 है
जो 3 से विभाज्य नहीं है।
अतः दी गई संख्या 6 से विभाज्य नहीं है।

(i) दी गई संख्या = 639210
दी गई संख्या के इकाई स्थान का अंक 0 है।
अतः यह 2 से विभाज्य है।
दी गई संख्या 639210 के सभी अंकों का योग
= 6 + 3 + 9 + 2 + 1 + 0 = 21 है जो 3 से विभाज्य है।
अतः दी गई संख्या 6 से विभाज्य है।

(j) दी गई संख्या = 17852
दी गई संख्या का इकाई अंक सम है।
अतः यह 2 से विभाज्य है।
दी गई संख्या 17852 के सभी अंकों का योग
= 1 + 7 + 8 + 5 + 2 = 23 है जो 3 से विभाज्य नहीं है।
अतः दी गई संख्या 6 से विभाज्य नहीं है।

प्रश्न 4.
विभाज्यता परीक्षणों का उपयोग करके, निर्धारित करें कि निम्नलिखित में से कौन सी संख्या 11 से विभाज्य है:
(a) 5445
(b) 10824
(c) 7138965
(d) 70169308
(e) 10000001.
हल: हम जानते हैं कि एक संख्या 11 से विभाज्य है यदि संख्या के विषम स्थानों (दाएं से) के अंकों के योग और सम स्थानों (दाएं से) के अंकों के योग के बीच का अंतर या तो 0 है या 11 से विभाज्य है।
(a) दी गई संख्या = 5445
विषम स्थानों पर अंकों का योग = 5 + 4 = 9
सम स्थानों पर अंकों का योग = 4 + 5 = 9
अंतर = 9 - 9 = 0
इसलिए, दी गई संख्या 11 से विभाज्य है।

(b) दी गई संख्या = 10824
विषम स्थानों पर अंकों का योग = 4 + 8 + 1 = 13
सम स्थानों पर अंकों का योग = 2 + 0 = 2
अंतर = 13 - 2 = 11
जो 11 से विभाज्य है।
अतः दी गई संख्या 11 से विभाज्य है।

(c) दी गई संख्या = 7138965
विषम स्थानों पर अंकों का योग = 5 + 9 + 3 + 7 = 24
सम स्थानों पर अंकों का योग = 6 + 8 + 1 = 15
अंतर = 24 - 15 = 9
जो 11 से विभाज्य नहीं है।
अतः दी गई संख्या 11 से विभाज्य नहीं है।

(d) दी गई संख्या = 70169308
विषम स्थानों पर सभी अंकों का योग = 8 + 3 + 6 + 0 = 17
सम स्थानों पर सभी अंकों का योग = 0 + 9 + 1 + 7 = 17
अंतर = 17-17 = 0
अतः दी गई संख्या 11 से विभाज्य है।

(e) दी गई संख्या = 10000001
विषम स्थानों पर सभी अंकों का योग = 1 + 0 + 0 + 0 = 1
सम स्थानों पर सभी अंकों का योग = 0 + 0 + 0 + 1 = 1
अंतर = 1 - 1 = 0
अतः दी गई संख्या 11 से विभाज्य है।

प्रश्न 5.
निम्नलिखित संख्याओं में से प्रत्येक के रिक्त स्थान में सबसे छोटा अंक और सबसे बड़ा अंक लिखिए ताकि बनने वाली संख्या 3 से विभाज्य हो।
(a) ____ 6724
(b) 4765 ____ 2
हल:
हम जानते हैं कि संख्या 3 से विभाज्य है यदि संख्या के सभी अंकों का योग भी 3 से विभाज्य है।
(a) ___ 6724
अंकों का योग = 4 + 2 + 7 + 6 = 19
रिक्त स्थान पर रखा जाने वाला सबसे छोटा अंक = 2
​​फिर योग = 19 + 2 = 21 जो 3 से विभाज्य है।
रिक्त स्थान में रखा जाने वाला सबसे बड़ा अंक = 8
फिर, योग = 19 + 8 = 27 जो 3 से विभाज्य है
इसलिए, आवश्यक अंक 2 और 8 हैं।

(b) 4765 ____ 2.
अंकों का योग = 2 + 5 + 6 + 7 + 4 = 24
रिक्त स्थान में रखे जाने वाले सबसे छोटे अंक = 0
तो, योग = 24 + 0 = 24
जो 3 से विभाज्य है।
रिक्त स्थान में रखा जाने वाला सबसे बड़ा अंक = 9
तो, योग = 24 + 9 = 33 जो 3 से विभाज्य है।
इसलिए, आवश्यक अंक 0 और 9 हैं।

प्रश्न 6.
निम्नलिखित प्रत्येक संख्या के रिक्त स्थान में एक अंक लिखें ताकि बनने वाली संख्या 11 से विभाज्य हो।
(a) 92 ___ 389
(b) 8 ___ 9484
हल:
(a) 92 ___ 389
विषम स्थानों पर अंकों का योग = 9 + 3 + 2 = 14
सम स्थानों पर अंकों का योग = 8 + ( ) + 9 = 17
अंतर = 17 + ( ) – 14 = ( ) + 3
दी गई संख्या को 11 से विभाज्य होने के लिए
( ) + 3 = 11
∴ ( ) = 11 – 3 = 8
तो, लुप्त अंक = 8
इसलिए, आवश्यक संख्या 928389 है।

(b) 8 ___ 9484
विषम स्थानों पर अंकों का योग = 4 + 4 + ( ) = 8 + ( )
सम स्थानों पर अंकों का योग = 8 + 9 + 8 = 25
∴ अंतर = 25 – [8 + ( )]
= 25 – 8 – ( ) = 17 – ( )
दी गई संख्या को 11 से विभाज्य होने के लिए
17 – 0 = 11
∴ 17 – 11 = 6
तो, लुप्त अंक = 6
इसलिए, आवश्यक संख्या = 869484.

Ex 3.4

प्रश्न 1.
इनके सामान्य गुणनखंड ज्ञात कीजिए:
(a) 20 और 28
(b) 15 और 25
(c) 35 और 50
(d) 56 और 120
हल:
(a) दी गई संख्याएँ हैं: 20 और 28
20 के गुणनखंड 1, 2, 4, 5, 10, 20 हैं
28 के गुणनखंड 1, 2, 4, 7, 28 हैं
इसलिए, सामान्य गुणनखंड 1, 2 और 4 हैं।

(b) दी गई संख्याएँ हैं: 15 और 25
15 के गुणनखंड 1, 3, 5, 15 हैं
25 के गुणनखंड 1, 5, 25 हैं
अतः, सामान्य गुणनखंड 1 और 5 हैं।

(c) दी गई संख्याएँ हैं: 35 और 50
35 के गुणनखंड हैं: 1, 5, 7, 35
50 के गुणनखंड हैं: 1, 2, 5, 10, 50
अतः, सामान्य गुणनखंड 1 और 5 हैं।

(d) दी गई संख्याएँ हैं: 56 और 120
56 के गुणनखंड 1, 2, 4, 7, 8, 14, 28, 56
हैं 120 के गुणनखंड 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 30, 40, 60, 120 हैं
इसलिए, सामान्य गुणनखंड 1, 2, 4 और 8 हैं।

प्रश्न 2.
इनके सामान्य गुणनखंड ज्ञात कीजिए:
(a) 4, 8 और 12
(b) 5, 15 और 25
(6) 8 9484
हल:
(a) दी गई संख्याएँ हैं: 4, 8 और 12
4 के गुणनखंड 1, 2, 4 हैं
8 के गुणनखंड 1, 2, 4, 8
हैं 12 के गुणनखंड 1, 2, 3, 4, 6, 12 हैं
इसलिए, सामान्य गुणनखंड 1, 2 और 4 हैं।

(b) दी गई संख्याएँ हैं: 5, 15 और 25
5 के गुणनखंड 1, 5 हैं
15 के गुणनखंड 1, 3, 5, 15
हैं 25 के गुणनखंड 1, 5, 25 हैं
अतः, सामान्य गुणनखंड 1 और 5 हैं।

प्रश्न 3.
इनके प्रथम तीन गुणज ज्ञात कीजिए:
(a) 6 और 8
(b) 12 और 18
हल:
(a) दी गई संख्याएँ 6 और 8
हैं 6 के प्रथम तीन गुणज
6 x 1= 6; 6 x 2 = 12; 6 x 3 = 18 हैं।
8 के प्रथम तीन गुणज
8 x 1 = 8; 8 x 2 = 16; 8 x 3 = 24 हैं।

(b) दी गई संख्याएँ 12 और 18 हैं।
12 के पहले तीन गुणज
12 x 1 = 12;
12 x 2 = 24;
12 x 1 = 36;
18 के पहले तीन गुणज
18 x 1 = 18;
18 x 2 = 36;
18 x 3 = 54 हैं।

प्रश्न 4.
100 से छोटी सभी संख्याएँ लिखिए जो 3 और 4 के सार्व गुणज हैं।
हल:
दी गई संख्याएँ 3 और 4 हैं।
100 से कम 3 के गुणज हैं:

अतः, 100 से कम 3 और 4 के सार्व गुणज हैं: 12, 24, 36, 48, 60, 72, 84 और 96।

प्रश्न 5.
निम्नलिखित में से कौन सी संख्याएँ सह-अभाज्य हैं?
(a) 18 और 35
(b) 15 और 37
(c) 30 और 415
(d) 17 और 68
(e) 216 और 215
(f) 81 और 16
हल:
(a) दी गई संख्याएँ 18 और 35 हैं।
18 के गुणनखंड 1, 2, 3, 6, 9, 18 हैं।
35 के गुणनखंड 1, 5, 7, 35 हैं।
चूँकि, 18 और 35 का सार्व गुणनखंड केवल 1 है।
इसलिए, 18 और 35 सह-अभाज्य हैं।

(b) दी गई संख्याएँ 15 और 37 हैं।
15 के गुणनखंड 1, 3, 5, 15 हैं।
37 के गुणनखंड 1, 37 हैं।
चूँकि 15 और 37 का सार्व गुणनखंड केवल 1 है।
अतः वे सह-अभाज्य हैं।

(c) दी गई संख्याएँ 30 और 415 हैं।
30 के गुणनखंड 1, 2, 3, 5, 6, 15, 30 हैं।
415 के गुणनखंड 1, 5, 83 हैं।
चूँकि, संख्याओं के उभयनिष्ठ गुणनखंड 1 और 5 हैं
, इसलिए वे सह-अभाज्य नहीं हैं।

(d) दी गई संख्याएँ 17 और 68 हैं।
17 के गुणनखंड 1, 17 हैं।
68 के गुणनखंड 1, 2, 4, 17, 34, 68 हैं।
चूँकि, संख्याओं के उभयनिष्ठ गुणनखंड 1 और 17 हैं
, इसलिए, वे सह-अभाज्य नहीं हैं।

(e) दी गई संख्याएँ 216 और 215 हैं।
216 के गुणनखंड 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 54, 72, 108, 216
हैं। 215 के गुणनखंड 1, 5, 43 हैं।
चूँकि 216 और 215 का सार्व गुणनखंड केवल 1 है।
इसलिए, वे सह-अभाज्य हैं।

(f) दी गई संख्याएँ 81 और 16 हैं।
81 के गुणनखंड 1, 3, 9, 27, 81 हैं।
16 के गुणनखंड 1, 2, 4, 8, 16 हैं।
चूँकि 81 और 16 में केवल 1 ही उभयनिष्ठ है
, इसलिए ये सह-अभाज्य हैं।

प्रश्न 6.
एक संख्या 5 और 12 दोनों से विभाज्य है। वह संख्या किस अन्य संख्या से सदैव विभाज्य होगी?
हल:
यदि वह संख्या 5 और 12 दोनों से विभाज्य है, तो वह संख्या 5 x 12 अर्थात् 60 से भी विभाज्य होगी।

प्रश्न 7.
एक संख्या 12 से विभाज्य है। वह संख्या किस अन्य संख्या से विभाज्य होगी?
हल:
12 के गुणनखंड 1, 2, 3, 4, 6, 12 हैं।
अतः जो संख्या 12 से विभाज्य है, वह अपने गुणनखंडों अर्थात् 1, 2, 3, 4, 6 और 12 से भी विभाज्य होगी।

Ex 3.5

प्रश्न 1.
निम्नलिखित में से कौन से कथन सत्य हैं?
(a) यदि कोई संख्या 3 से विभाज्य है, तो उसे 9 से भी विभाज्य होना चाहिए।
(b) यदि कोई संख्या 9 से विभाज्य है, तो उसे 3 से भी विभाज्य होना चाहिए।
(c) एक संख्या 18 से विभाज्य होती है, यदि वह 3 और 6 दोनों से विभाज्य हो।
(d) यदि कोई संख्या 9 और 10 दोनों से विभाज्य हो, तो उसे 90 से भी विभाज्य होना चाहिए।
(e) यदि दो संख्याएँ सह-अभाज्य हैं, तो उनमें से कम से कम एक अभाज्य होनी चाहिए।
(f) सभी संख्याएँ जो 4 से विभाज्य हैं, उन्हें 8 से भी विभाज्य होना चाहिए।
(g) सभी संख्याएँ जो 8 से विभाज्य हैं, उन्हें 4 से भी विभाज्य होना चाहिए।
(h) यदि कोई संख्या दो संख्याओं को अलग-अलग पूर्णतः विभाजित करती है, तो उसे उनके योग को पूर्णतः विभाजित करना चाहिए।
(i) यदि कोई संख्या दो संख्याओं के योग को पूर्णतः विभाजित करती है, तो उसे दोनों संख्याओं को अलग-अलग पूर्णतः विभाजित करना होगा।
हल:
(a) असत्य
(b) सत्य
(c) असत्य
(d) सत्य
(e) असत्य
(f) असत्य
(g) सत्य
(h) सत्य
(i) असत्य

प्रश्न 2.
यहाँ 60 के लिए दो अलग-अलग गुणनखंड वृक्ष दिए गए हैं। लुप्त संख्याएँ लिखिए।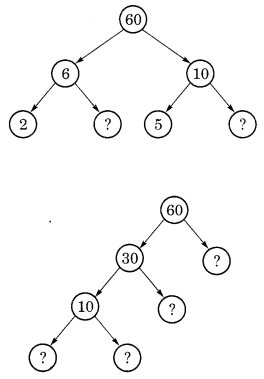

हल:
दिया गया है: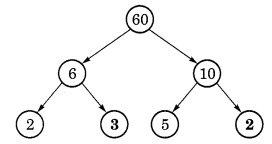

यहाँ, 6 = 2 x लुप्त संख्या
∴ लुप्त संख्या = 6 · 2 = 3
इसी प्रकार, 10 = 5 x लुप्त संख्या
∴ लुप्त संख्या = 10 ÷ 5 = 2
अतः, लुप्त संख्याएँ 3 और 2 हैं।

(b) दिया गया है कि: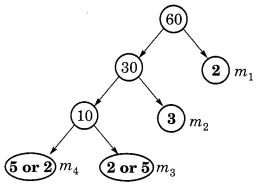

लुप्त संख्याएँ m 1 , m 2 , m 3  और m 4 हैं ।
60 = 30 x m 1
⇒ m 1  = 60 ÷ 30 = 2
30 = 10 x m 2
⇒ m 2  = 30 ÷ 10 = 3
10 = m 3  x m 4
⇒ m 3  = 2 या 5 और m 4  = 5 या 2
अतः, लुप्त संख्याएँ 2, 3, 2, 5 हैं।

प्रश्न 3.
एक भाज्य संख्या के अभाज्य गुणनखंडन में कौन से गुणनखंड शामिल नहीं होते हैं?
हल:
एक भाज्य संख्या के अभाज्य गुणनखंडन में 1 और संख्या स्वयं शामिल नहीं होते हैं।

प्रश्न 4.
चार अंकों की सबसे बड़ी संख्या लिखिए और उसे उसके अभाज्य गुणनखंडों के रूप में व्यक्त कीजिए।
हल:
चार अंकों की सबसे बड़ी संख्या = 9999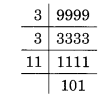

अतः, 9999 के अभाज्य गुणनखंड = 3 x 3 x 11 x 101.

प्रश्न 5.
पाँच अंकों की सबसे छोटी संख्या लिखिए और उसे उसके अभाज्य गुणनखंडों के रूप में व्यक्त कीजिए।
हल:
पाँच अंकों की सबसे छोटी संख्या = 10000

अतः, अभीष्ट अभाज्य गुणनखंड: 10000 = 2 x 2 x 2 x 5 x 5 x 5 x 5.

प्रश्न 6.
1729 के सभी अभाज्य गुणनखंड ज्ञात कीजिए और उन्हें आरोही क्रम में व्यवस्थित कीजिए। अब दो क्रमागत अभाज्य गुणनखंडों के बीच संबंध, यदि कोई हो, बताइए।
हल:
दी गई संख्या = 1729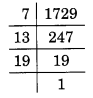

अतः, 1729 के अभाज्य गुणनखंड = 7 x 13 x 19.
यहाँ, 13 – 7 = 6 और 19 – 13 = 6
हम देखते हैं कि दो क्रमागत अभाज्य गुणनखंडों का अंतर 6 है।

प्रश्न 7.
तीन क्रमागत संख्याओं का गुणनफल सदैव 6 से विभाज्य होता है। कुछ उदाहरणों की सहायता से इस कथन की पुष्टि कीजिए।
हल:
उदाहरण 1:
तीन क्रमागत संख्याएँ 20, 21 और 22 लीजिए।
यहाँ 20, 2 से विभाज्य है और 21, 3 से विभाज्य है।
अतः गुणनफल 20 x 21 x 22 = 9240, 6 से विभाज्य है।

उदाहरण 2:
तीन क्रमागत संख्याएँ 30; 31 और 32 लीजिए।
यहाँ 30, 3 से विभाज्य है और 32, 2 से विभाज्य है।
इसलिए, गुणनफल 30 x 31 x 32 = 29760, 6 से विभाज्य है।

उदाहरण 3:
तीन क्रमागत संख्याएँ 48, 49 और 50 लीजिए।
यहाँ, 48, 3 से विभाज्य है और 50, 2 से विभाज्य है।
इसलिए, गुणनफल 48 x 49 x 50 = 117600 है जो 6 से विभाज्य है।

प्रश्न 8.
दो क्रमागत विषम संख्याओं का योग 4 से विभाज्य होता है। कुछ उदाहरणों की सहायता से इस कथन की पुष्टि कीजिए।
हल:
उदाहरण 1:
आइए दो क्रमागत विषम संख्याएँ 97 और 99 लें।
योग = 97 + 99 = 196
यहाँ, अंतिम दो अंकों से बनी संख्या 96 है जो 4 से विभाज्य है।
अतः, संख्याओं 97 और 99 का योग अर्थात् 196, 4 से विभाज्य है।

उदाहरण 2:
आइए दो क्रमागत विषम संख्याएँ 121 और 123 लें।
योग = 121 + 123 = 244
यहाँ, अंतिम दो अंकों से बनी संख्या 44 है जो 4 से विभाज्य है।

उदाहरण 3:
आइए दो क्रमागत विषम संख्याएँ 105 और 107 लें।
योग = 105 + 107 = 212
यहाँ, अंतिम दो अंकों से बनी संख्या 12 है जो 4 से विभाज्य है।

प्रश्न 9.
निम्नलिखित में से किस व्यंजक में अभाज्य गुणनखंडन किया गया है?
(a) 24 = 2 x 3 x 4
(b) 56 = 7 x 2 x 2 x 2
(c) 70 = 2 x 5 x 7
(d) 54 = 2 x 3 x 9.
हल:
(a) 24 = 2 x 3 x 4
यहाँ, 4 एक अभाज्य संख्या नहीं है।
अतः, 24 = 2 x 3 x 4 एक अभाज्य गुणनखंडन नहीं है।

(b) 56 = 7 x 2 x 2 x 2
यहाँ, सभी गुणनखंड अभाज्य संख्याएँ हैं।
अतः, 56 = 7 x 2 x 2 x 2 एक अभाज्य गुणनखंड है।

(c) 70 = 2 x 5 x 7
यहाँ, सभी गुणनखंड अभाज्य संख्याएँ हैं।
अतः, 70 = 2 x 5 x 7 एक अभाज्य गुणनखंड है।

(d) 54 = 2 x 3 x 9
यहाँ, 9 एक अभाज्य संख्या नहीं है।
अतः, 54 = 2 x 3 x 9 एक अभाज्य गुणनखंड नहीं है।

प्रश्न 10.
ज्ञात कीजिए कि क्या 25110, 45 से विभाज्य है।
हल:
45 = 5 x 9
यहाँ, 5 और 9 सह-अभाज्य संख्याएँ हैं।
5 से विभाज्यता परीक्षण: दी गई संख्या 25110 का इकाई अंक 0 है। अतः यह 5 से विभाज्य है।
9 से विभाज्यता परीक्षण:
अंकों का योग = 2 + 5 + l + l + 0 = 9 जो 9 से विभाज्य है।
अतः दी गई संख्या 5 और 9 दोनों से विभाज्य है। अतः, संख्या 25110, 45 से विभाज्य है।

प्रश्न 11.
18, 2 और 3 दोनों से विभाज्य है। यह 2 x 3 = 6 से भी विभाज्य है। इसी प्रकार, एक संख्या 4 और 6 दोनों से विभाज्य है। क्या हम कह सकते हैं कि वह संख्या 4 x 6 = 24 से भी विभाज्य होगी? यदि नहीं, तो अपने उत्तर की पुष्टि के लिए एक उदाहरण दीजिए।
हल:
यहाँ, दी गई दो संख्याएँ सह-अभाज्य नहीं हैं। इसलिए, यह आवश्यक नहीं है कि 4 और 6 दोनों से विभाज्य संख्याएँ अपने गुणनफल 4 x 6 = 24 से भी विभाज्य हों।
उदाहरण: 36 और 60, 4 से विभाज्य हैं, 4 और 6 दोनों से, लेकिन 24 से नहीं।

प्रश्न 12.
मैं सबसे छोटी संख्या हूँ, जिसके चार अलग-अलग अभाज्य गुणनखंड हैं। क्या आप मुझे ज्ञात कर सकते हैं?
हल:
हम जानते हैं कि सबसे छोटी 4 अभाज्य संख्याएँ 2, 3, 5 और 7 हैं।
अतः, अभीष्ट संख्या = 2 x 3 x 5 x 7 = 210

Ex 3.6

प्रश्न 1.
निम्नलिखित संख्याओं का HCF ज्ञात कीजिए:
(a) 18, 48
(b) 30, 42
(c) 18, 60
(d) 27, 63
(e) 36, 84
(f) 34, 102
(g) 70, 105, 175
(h) 91, 112, 49
(i) 18, 54, 81
(j) 12, 45, 75
हल:
(a) दी गई संख्याएँ 18 और 48 हैं।
18 और 48 के अभाज्य गुणनखंड हैं: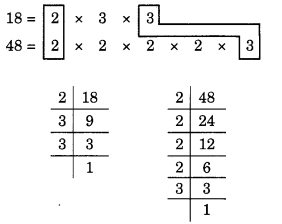

यहाँ, सामान्य कारक 2 और 3 हैं।
इसलिए, HCF = 2 x 3 = 6।

(b) दी गई संख्याएँ 30 और 42 हैं।
30 और 42 के अभाज्य गुणनखंड हैं: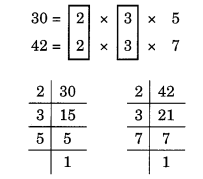

यहाँ, सामान्य गुणनखंड 2 और 3 हैं।
इसलिए, HCF = 2 x 3 = 6.

(c) दी गई संख्याएँ 18 और 60 हैं।
18 और 60 के अभाज्य गुणनखंड हैं: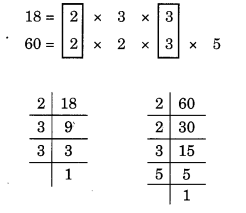

यहाँ, सामान्य गुणनखंड 2 और 3 हैं।
इसलिए, 18 और 60 का HCF = 2 x 3 = 6.

(d) दी गई संख्याएँ 27 और 63 हैं।
27 और 63 के अभाज्य गुणनखंड इस प्रकार हैं: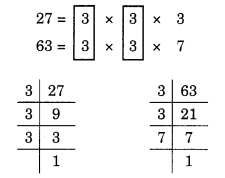

यहाँ, सार्व गुणनखंड 3 है (दो बार आता है)।
अतः, HCF = 3 x 3 = 9 है।

(e) दी गई संख्याएँ 36 और 84 हैं।
36 और 84 के अभाज्य गुणनखंड हैं: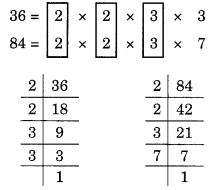

यहाँ, सामान्य गुणनखंड 2, 2 और 3 हैं।
इसलिए, HCF = 2 x 2 x 3 = 12.

(च) दी गई संख्याएँ 34 और 102 हैं।
34 और 102 के अभाज्य गुणनखंड हैं: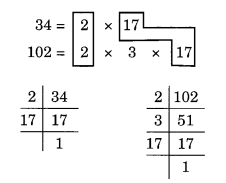

यहाँ, सामान्य गुणनखंड 2 और 17 हैं।
इस प्रकार, HCF 2 x 17 = 34 है।

(g) दी गई संख्याएँ 70, 105 और 175 हैं।
70, 105 और 175 के अभाज्य गुणनखंड हैं: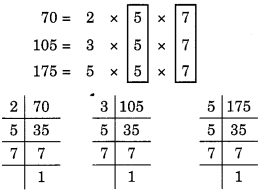

यहाँ, सामान्य गुणनखंड 5 और 7 हैं।
इसलिए, 70, 105 और 175 का HCF 5 x 7 = 35 है।

(h) दी गई संख्याएँ 91, 112 और 49 हैं।
91, 112 और 49 के अभाज्य गुणनखंड हैं: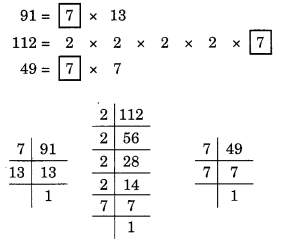

यहाँ, सार्व गुणनखंड 7 है।
अतः, HCF = 7 है।

(i) दी गई संख्याएँ 18, 54 और 81 हैं।
18, 54 और 81 के अभाज्य गुणनखंड इस प्रकार हैं: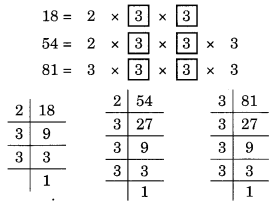

यहाँ, सार्व गुणनखंड 3 है (दो बार आता है)।
अतः, HCF = 3 x 3 = 9 है।

(j) दी गई संख्याएँ 12, 45 और 75 हैं।
12, 45 और 75 के अभाज्य गुणनखंड हैं: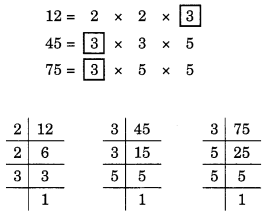

यहाँ, सार्व गुणनखंड 3 है।
अतः, HCF = 3 है।

प्रश्न 2.

दो क्रमागत (a) संख्याओं
का HCF क्या है ? (b) सम संख्याएँ? (c) विषम संख्याएँ? हल: (a) दो क्रमागत संख्याओं का सार्व गुणनखंड हमेशा 1 होता है। अतः, HCF = 1 है। (b) दो क्रमागत सम संख्याओं के सार्व गुणनखंड 1 और 2 हैं। अतः, HCF = 1 x 2 = 2 है। (c) दो क्रमागत विषम संख्याओं का सार्व गुणनखंड 1 है। अतः, HCF = 1 है।

प्रश्न 3.
सह-अभाज्य संख्याओं 4 और 15 का HCF गुणनखंडन द्वारा निम्न प्रकार ज्ञात किया गया:
4 = 2 x 2 और 15 = 3 x 15. चूँकि कोई उभयनिष्ठ अभाज्य गुणनखंड नहीं है, इसलिए 4 और 15 का HCF 0 है।
क्या उत्तर सही है? यदि नहीं, तो सही HCF क्या है?
हल:
नहीं, उत्तर सही नहीं है।
कारण: 0 किसी भी संख्या का अभाज्य गुणनखंड नहीं है।
1 हमेशा सह-अभाज्य संख्या का अभाज्य गुणनखंड होता है।
अतः, 4 और 15 का सही HCF 1 है।

Ex 3.7

प्रश्न 1.
रेणु 75 किग्रा और 69 किग्रा वजन के उर्वरक के दो बैग खरीदती है। वजन का वह अधिकतम मान ज्ञात कीजिए जो उर्वरक के वजन को सटीक संख्या में बार माप सके।
हल:
वजन का वह अधिकतम मान जो दिए गए वजन को सटीक संख्या में बार माप सके = 75 ग्राम और 69 किग्रा का HCF
75 और 69 के अभाज्य गुणनखंड हैं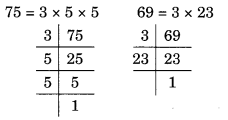

यहाँ, सार्व गुणनखंड 3 है।
∴ 75 और 69 का HCF = 3 है।
अतः, वजन का अभीष्ट अधिकतम मान = 3 किग्रा है।

प्रश्न 2.
तीन लड़के एक ही स्थान से एक साथ कदम मिलाकर चलते हैं। उनके कदमों की माप क्रमशः 63 सेमी, 70 सेमी और 77 सेमी है। प्रत्येक को कितनी न्यूनतम दूरी तय करनी चाहिए ताकि सभी पूरे कदम चलकर दूरी तय कर सकें?
हल:
प्रत्येक लड़के को चलने वाली न्यूनतम दूरी उनके कदमों के माप का लघुत्तम समापवर्त्य (LCM) होनी चाहिए।
63, 70 और 77 का LCM ज्ञात करने के लिए, हम विभाजन विधि का उपयोग करते हैं।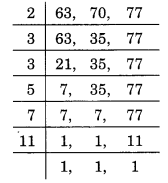

∴ 63, 70 और 77 का LCM = 2 x 3 x 3 x 5 x 7 x 11 = 6930
अतः, आवश्यक न्यूनतम दूरी = 6930 सेमी।

प्रश्न 3.
एक कमरे की लंबाई, चौड़ाई और ऊँचाई क्रमशः 825 सेमी, 675 सेमी और 450 सेमी है। वह सबसे लंबा फीता ज्ञात कीजिए जो कमरे के तीनों आयामों को सटीक रूप से माप सके।
हल:
कमरे के तीनों आयामों को मापने के लिए आवश्यक सबसे लंबा फीता = 825, 675 और 450 का म.स.प.
825, 675 और 450 के अभाज्य गुणनखंड हैं
825 = 3 x 5 x 5 x 11
675 = 3 x 3 x 3 x 5 x 5
450 = 2 x 3 x 3 x 5 x 5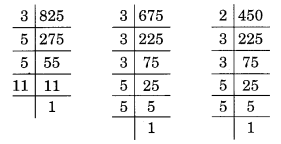

यहाँ, उभयनिष्ठ गुणनखंड 3, 5 (दो गुना) हैं।
∴ 825, 675 और 450 का म.स.प. = 3 x 5 x 5 = 75
अतः, आवश्यक सबसे लंबा फीता = 75 सेमी

प्रश्न 4.
3 अंकों की सबसे छोटी संख्या ज्ञात कीजिए जो 6, 8 और 12 से पूर्णतः विभाज्य हो।
हल:
3 अंकों की सबसे छोटी संख्या = 100
क्योंकि 6, 8 और 12 का LCM इनसे विभाज्य है।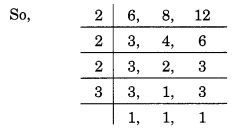

∴ 6, 8 और 12 का LCM = 2 x 2 x 2 x 3 = 24
चूँकि, 24 के सभी गुणज 6, 8 और 12 से भी विभाज्य होंगे।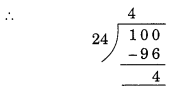

इसलिए, तीन अंकों में 24 का सबसे छोटा गुणज
100 से ठीक ऊपर होगा = (100 – 4) + 24 = 96 + 24 = 120
अतः, अभीष्ट संख्या 120 है।

प्रश्न 5.
8, 10 और 12 से पूर्णतः विभाज्य सबसे बड़ी 3-अंकीय संख्या ज्ञात कीजिए।
हल:
8, 10 और 12 का LCM ज्ञात करने के लिए, हमारे पास है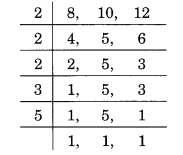

∴ 8, 10 और 12 का LCM = 2 x 2 x 2 x 3 x 5 = 120
सबसे बड़ी 3-अंकीय संख्या = 999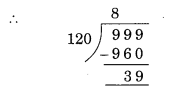

∴ 999 के ठीक नीचे 120 का गुणज 960 है।
अतः अभीष्ट संख्या 960 है।

प्रश्न 6.
तीन अलग-अलग सड़क क्रॉसिंग पर ट्रैफिक लाइटें क्रमशः प्रत्येक 48 सेकंड, 72 सेकंड और 108 सेकंड के बाद बदलती हैं। यदि वे सुबह 7 बजे एक साथ बदलती हैं, तो वे फिर से एक साथ किस समय बदलेंगी?
हल:
48, 72 और 108 का LCM ज्ञात करने के लिए, हमारे पास है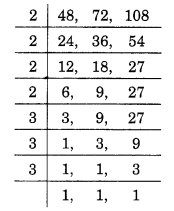

: ∴ LCM = 2 x 2 x 2 x 3 x 3 x 3= 432
अतः, 432 सेकंड के बाद, लाइट एक साथ बदल जाएगी।
अतः, आवश्यक समय = 432 सेकंड = 7 मिनट 12 सेकंड अर्थात, सुबह 7 बजकर 7 मिनट 12 सेकंड

प्रश्न 7.
तीन टैंकरों में क्रमशः 403 लीटर, 434 लीटर और 465 लीटर डीज़ल है। उस बर्तन की अधिकतम धारिता ज्ञात कीजिए जो तीनों बर्तनों के डीज़ल को ठीक-ठीक संख्या में माप सके।
हल:
आवश्यक माप की अधिकतम धारिता 403, 434 और 465 के HCF के बराबर है।
403, 434 और 465 के अभाज्य गुणनखंडन हैं।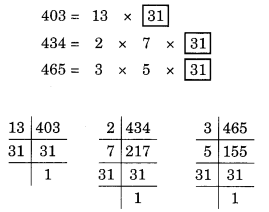

उभयनिष्ठ गुणनखंड = 31 है
। अतः, 403, 434 और 465 का HCF = 31 है।
अतः, आवश्यक बर्तन की अधिकतम धारिता = 31 लीटर है।

प्रश्न 8.
वह सबसे छोटी संख्या ज्ञात कीजिए जिसे 6, 15 और 18 से विभाजित करने पर प्रत्येक स्थिति में शेष 5 बचे।
हल:
6, 15 और 18 का LCM ज्ञात करने के लिए, हमारे पास है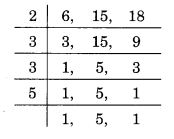

: ∴ 6, 15 और 18 का LCM = 2 x 3 x 3 x 5 = 90.
यहाँ, 90 वह सबसे छोटी संख्या है जो 6, 15 और 18 से पूर्णतः विभाज्य है।
शेष 5 प्राप्त करने के लिए, सबसे छोटी संख्या 90 + 5 = 95 होगी।
अतः अभीष्ट संख्या 95 है।

प्रश्न 9.
18, 24 और 32 से विभाज्य सबसे छोटी 4-अंकीय संख्या ज्ञात कीजिए।
हल:
सबसे छोटी 4-अंकीय संख्या = 1000।
18, 24 और 32 का LCM ज्ञात करने के लिए, हमारे पास है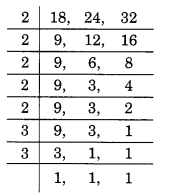

: ∴ LCM = 2 x 2 x 2 x 2 x 3 x 3 = 288
चूँकि, 288 सबसे छोटी संख्या है जो 18, 24 और 32 से पूर्णतः विभाज्य है।
लेकिन यह 4-अंकीय संख्या नहीं है।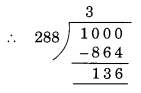

अतः, 1000 के ठीक ऊपर 288 का गुणज है: 1000 - 136 + 288 = 1152।
अतः, अभीष्ट संख्या 1152 है।

प्रश्न 10.
निम्नलिखित संख्याओं का LCM ज्ञात कीजिए:
(a) 9 और 4
(b) 12 और 5
(c) 6 और 5
(d) 15 और 4
प्राप्त LCM में एक उभयनिष्ठ गुणधर्म देखिए। क्या प्रत्येक स्थिति में LCM दो संख्याओं का गुणनफल है?
हल:
(a) 9 और 4 का LCM ज्ञात करने के लिए, हमारे पास है

∴ LCM = 2 x 2 x 3 x 3 = 36.
9 और 4 का गुणनफल = 9 x 4 = 36.
अतः, 9 और 4 का LCM = 9 और 4 का गुणनफल।

(b) 12 और 5 का LCM ज्ञात करने के लिए, हमारे पास है

∴ LCM = 2 x 2 x 3 x 5 = 60.
12 और 5 का गुणनफल = 12 x 5 = 60.
अतः, 12 और 5 का LCM = 12 और 5 का गुणनफल।

(c) 6 और 5 का LCM ज्ञात करने के लिए, हमारे पास है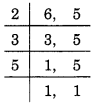

∴ LCM = 2 x 3 x 5 = 30.
6 और 5 का गुणनफल = 6 x 5 = 30.
अतः, 6 और 5 का LCM = 6 और 5 का गुणनफल।

(d) 15 और 4 का LCM ज्ञात करने के लिए, हमारे पास है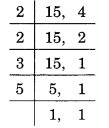

∴ LCM = 2 x 2 x 3 x 5 = 60.
संख्याओं 15 और 4 का गुणनफल = 15 x 4 = 60.
अतः, 15 और 4 का LCM = 15 और 4 का गुणनफल।

प्रश्न 11.
निम्नलिखित संख्याओं का LCM ज्ञात कीजिए जिसमें एक संख्या दूसरी का गुणनखंड है।
(a) 5, 20
(b) 6, 18
(c) 12, 48
(d) 9, 45
प्राप्त परिणामों में आप क्या देखते हैं?
हल:
(a) 5 और 20 का LCM ज्ञात करने के लिए, हमारे पास है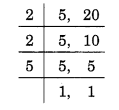

∴ LCM = 2 x 2 x 5 = 20.
अतः, 5 और 20 का LCM = 20 है।

(b) 6 और 18 का LCM ज्ञात करने के लिए, हमारे पास है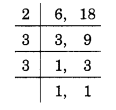

∴ LCM = 2 x 3 x 3 = 18.
अतः, 6 और 18 का LCM = 18.

(c) 12 और 48 का LCM ज्ञात करने के लिए, हमारे पास

LCM = 2 x 2 x 2 x 2 x 3 = 48 है
। अतः, 12 और 48 का LCM = 48 है।

(d) 9 और 45 का LCM ज्ञात करने के लिए, हमारे पास है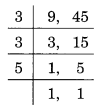

∴ LCM = 3 x 3 x 5 = 45.
अतः, 9 और 45 का LCM = 45.
उपरोक्त उदाहरणों से, हम देखते हैं कि दो संख्याओं का LCM, जहाँ एक संख्या दूसरी का गुणनखंड है, बड़ी संख्या है।

InText Questions

लघु उत्तरीय प्रश्न

प्रश्न 1.
सरल करें: 32 + 96 ÷ (7 + 9)
हल:
दिया गया है कि: 32 + 96 ÷ (7 + 9)
= 32 + 96 ÷ 16 (BODMAS का उपयोग करके)
= 32 + 6 = 38

प्रश्न 2.
सरल करें: 18 + {1 + (5 – 3) x 5}
हल:
दिया गया है कि: 18 + {1 + (5 – 3) x 5} (BODMAS का उपयोग करके)
= 18 + {1 + 2 x 5} = 18 + {1 + 10}
= 18 + 11 = 29.

प्रश्न 3.
बिना वास्तविक विभाजन के, दर्शाइए कि 11, 1,10,011 का एक गुणनखंड है।
हल:
यहाँ 1,10,011 = 1,10,000 + 11
= 11 x 10,000 + 11 x 1
= 11 x (10,000 + 1)
= 11 x 10,001
यह स्पष्ट है कि 11, 11 x 10,001 का एक गुणनखंड है।
अतः, 11, 1,10,011 का एक गुणनखंड है।

प्रश्न 4.
दो संख्याओं का योग 25 है और उनका गुणनफल 144 है। संख्याएँ ज्ञात कीजिए।
हल:
दो संख्याओं का गुणनफल 144 है।
∴ संभावित गुणनखंड 1 x 144, 2 x 72, 3 x 48, 4 x 36, 6 x 24, 8 x 18, 9 x 16, 12 x 12 हैं।
यहाँ, हम देखते हैं कि इन गुणनखंडों में से, हम 9 और 16 लेते हैं।
गुणनफल = 9 x 16 = 144 और योग = 9 + 16 = 25
अतः, अभीष्ट संख्याएँ 9 और 16 हैं।

प्रश्न 5.
क्या 80136, 11 से विभाज्य है?
हल:
विषम स्थानों के अंकों का योग = 6 + 1 + 8 = 15
सम स्थानों के अंकों का योग = 3 + 0 = 3
दोनों योगों का अंतर = 15 - 3 = 12,
जो न तो 0 है और न ही 11 का गुणज है।
अतः 80136, 11 से विभाज्य नहीं है।

प्रश्न 6.
दो संख्याओं के HCF और LCM क्रमशः 6 और 120 हैं। यदि उनमें से एक संख्या 24 है, तो दूसरी संख्या ज्ञात कीजिए।
हल:
दिया गया है: HCF = 6
LCM = 120
मान लीजिए दो संख्याएँ a और b हैं, जहाँ a = 24, b = ?
हम जानते हैं कि: axb = HCF x LCM
⇒ 24 xb = 6 x 120
⇒ b = ⇒ b = 30 अतः, दूसरी संख्या 30 है।6x12024

प्रश्न 7.
12 और 30 का LCM ज्ञात कीजिए।
हल:
दी गई संख्याएँ 12 और 30 हैं
12 = 2 x 2 x 3;
30 = 2 x 3 x 5
∴ LCM = 2 x 2 x 3 x 5 = 60
अतः, 12 और 30 का LCM = 60 है।

प्रश्न 8.
सबसे छोटी 4-अंकीय संख्या ज्ञात कीजिए जो 18, 24 और 32 से विभाज्य हो।
हल:
दी गई संख्याएँ 18, 24 और 32 हैं,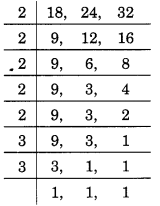

इस प्रकार, LCM = 2 x 2 x 2 x 2 x 3 x 3 = 288
सबसे छोटी 4-अंकीय संख्या = 1000
अब, हम 288 के गुणज तब तक लिखते हैं, जब तक हमें 4-अंकीय संख्या प्राप्त न हो जाए।
288 x 1 = 288, 288 x 2 = 576,
288 x 3 = 864, 288 x 4 = 1152
इसलिए, 1152 अभीष्ट संख्या है।

प्रश्न 9.
वह सबसे बड़ी संख्या ज्ञात कीजिए जिससे 82 और 132 को विभाजित करने पर क्रमशः 1 और 6 शेष बचे।
हल:
दी गई संख्याएँ 82 और 132 हैं और शेष क्रमशः 1 और 6 हैं।
82 – 1 = 81 और 132 – 6 = 126 है।
अतः, हमें 81 और 126 का HCF ज्ञात करना है।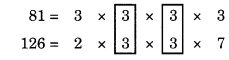

उभयनिष्ठ गुणनखंड 3 (दो बार आता है) है।
∴ HCF = 3 x 3 = 9
अतः, अभीष्ट संख्या 9 है।

प्रश्न 10.
वह सबसे बड़ी संख्या ज्ञात कीजिए जिससे 455, 582 और 710 को विभाजित करने पर क्रमशः 14, 15 और 17 शेष बचे।
हल:
दी गई संख्याएँ 455, 582 और 710 हैं और उनके क्रमशः शेषफल 14, 15 और 17 हैं।
455 – 14 = 441, 582 – 15 = 567 और 710 – 17 = 693 है।
अब इनका HCF ज्ञात कीजिए।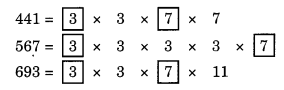

सार्व गुणनखंड 3 और 7 हैं।
∴ HCF = 3 x 7 = 21
अतः, अभीष्ट संख्या 21 है।

अति लघु उत्तरीय प्रश्न 

प्रश्न 1. किन्हीं दो (a) सम संख्याओं (b) विषम संख्याओं
का योग क्या होता है ? हल: (a) किन्हीं दो सम संख्याओं का योग सम होता है। उदाहरण: 4 (सम) + 6 (सम) = 10 (सम) (b) किन्हीं दो विषम संख्याओं का योग सम होता है। उदाहरण: 5 (विषम) + 7 (विषम) = 12 (सम)

प्रश्न 2.
निम्नलिखित में से कौन सी संख्या 3 से विभाज्य है?
(a) 1212
(b) 625
हल:
(a) दी गई संख्या = 1212
अंकों का योग = 1 + 2 + 1 + 2 = 6, जो 3 से विभाज्य है।
इसलिए, 1212 भी 3 से विभाज्य है।
(b) दी गई संख्या = 625
अंकों का योग = 6 + 2 + 5 = 13, जो 3 से विभाज्य नहीं है।
इसलिए, 625 3 से विभाज्य नहीं है।

प्रश्न 3.
यदि किन्हीं दो संख्याओं का LCM और HCF क्रमशः 15 और 4 है, तो संख्याओं का गुणनफल ज्ञात कीजिए।
हल:
हम जानते हैं कि संख्या का गुणनफल = LCM x HCF = 15 x 4 = 60
अतः, दी गई संख्याओं का गुणनफल = 60 है।

प्रश्न 4.
5 और 7 का HCF ज्ञात कीजिए।
हल:
दी गई संख्याएँ 5 और 7 हैं। हम देखते हैं कि 5 और 7 सह-अभाज्य संख्याएँ हैं।
अतः, HCF 1 है।

प्रश्न 5.
25 के प्रथम 3 गुणज लिखिए।
हल:
हमारे पास है 25 x 1 = 25; 25 x 2 = 50; 25 x 3 = 75
अतः, अभीष्ट गुणज 25, 50 और 75 हैं।

प्रश्न 6.
(a) 12 (b) 18 के संभावित गुणनखंड क्या हैं?
हल:
(a) 12 के संभावित गुणनखंड हैं:
12 = 1 x 12; 12 = 2 x 6; 12 = 3 x 4
अतः, 12 के गुणनखंड 1, 2, 3, 4, 6 और 12 हैं।

(b) 18 के संभावित गुणनखंड हैं:
18 = 1 x 18; 18 = 2 x 9; 18 = 3 x 6
अतः, 18 के गुणनखंड 1, 2, 3, 6, 9 और 18 हैं।

प्रश्न 7.
11 के प्रथम तीन गुणज लिखिए।
हल:
11 के प्रथम तीन गुणज हैं:
11 x 1 = 11; 11 x 2 = 22; 11 x 3 = 33
अतः, अभीष्ट गुणज हैं: 11, 22 और 33।

प्रश्न 8.
20 से छोटी अभाज्य जुड़वां संख्याओं के जोड़े लिखिए।
हल:
अभाज्य जुड़वां संख्याओं के जोड़े हैं: (3, 5), (5, 7), (11, 13), (17, 19)।

प्रश्न 9.
वह संख्या लिखिए जो सम और अभाज्य दोनों है।
हल:
2 एकमात्र सम संख्या है जो अभाज्य भी है।

प्रश्न 10.
अंकगणित का मूल प्रमेय क्या है?
हल:
1 से बड़ी प्रत्येक संख्या का केवल एक अभाज्य गुणनखंड होता है।

दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
निम्नलिखित को सरल करें:
40 + [20 – {28 ÷ 7 – 3 + (30 – 4 का 5)}]
हल:
BODMAS नियम का उपयोग करते हुए, हमारे पास है
40 + [20 – {28 ÷ 7 – 3 + (30 – 4 का 5)}]
= 40 + [20 – {28 ÷ 7 – 3 + (30 – 20)}]
= 40 + [20 – {28 ÷ 7 – 3 + 10}]
= 40 + [20 – [4 – 3 + 10}]
= 40 + [20-11] = 40 + 9 = 49.

प्रश्न 2.
अंग्रेजी, हिंदी और उर्दू पुस्तकों के तीन सेटों को इस तरह से रखा जाना है कि पुस्तकें विषयवार संग्रहीत हों और प्रत्येक ढेर की ऊंचाई समान हो। अंग्रेजी, हिंदी और उर्दू पुस्तकों की संख्या क्रमशः 336, 192 और 144 है। यह सुनिश्चित करते हुए कि पुस्तकों की मोटाई समान है, अंग्रेजी, हिंदी और उर्दू पुस्तकों के ढेर की संख्या निर्धारित करें।
समाधान:
पुस्तकों को आवश्यक तरीके से व्यवस्थित करने के लिए,
हमें सबसे बड़ी संख्या ज्ञात करनी होगी जो 336, 192 और 144 को पूर्ण रूप से विभाजित करती है।
इसलिए, 336, 192 और 144 का HCF है।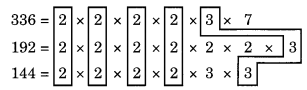

सामान्य कारक 2 x 2 x 2 x 2 x 3 = 48 हैं
। ∴ HCF = 48, अर्थात प्रत्येक ढेर में 48 पुस्तकें हैं।
∴ अंग्रेजी पुस्तकों के ढेरों की संख्या = 336 + 48 = 7
हिंदी पुस्तकों के ढेरों की संख्या = 192 4- 48 = 4
उर्दू पुस्तकों के ढेरों की संख्या = 144 4- 48 = 3

प्रश्न 3.
निम्नलिखित में से कौन से कथन सत्य हैं?
(a) 1371, 3 से विभाज्य है।
(b) 1155, 9 से विभाज्य नहीं है।
(c) 1478, 4 से विभाज्य नहीं है।
(d) 2470, 5 से विभाज्य है।
(e) यदि कोई संख्या 9 से विभाज्य है, तो वह 3 से भी विभाज्य होगी।
(f) यदि कोई संख्या 3 से विभाज्य है, तो वह 9 से भी विभाज्य होगी।
(g) किन्हीं दो विषम संख्याओं का योग सम होता है।
(h) यदि कोई संख्या 8 से विभाज्य है, तो वह 6 से भी विभाज्य होगी।
(i) यदि कोई संख्या 3 और 6 से विभाज्य है, तो वह 18 से विभाज्य होगी।
(j) 1758, 8 से विभाज्य नहीं है।
हल:
(a) हाँ, 1371, 3 से विभाज्य है। अतः यह सत्य कथन है।
(b) हाँ, 1155, 9 से विभाज्य नहीं है। इसलिए यह सत्य कथन है।
(c) हाँ, 1478, 4 से विभाज्य नहीं है। इसलिए
यह सत्य कथन है। (d) हाँ, 2470, 5 से विभाज्य है। इसलिए यह सत्य कथन है।
(e) हाँ, यह सत्य कथन है। यदि नहीं, तो यह सत्य कथन नहीं है।
(g) हाँ, यह सत्य कथन है।
(h) नहीं, यह सत्य कथन नहीं है।
(i) नहीं, यह सत्य कथन नहीं है।
(j) हाँ, यह सत्य कथन है।

बहुविकल्पीय प्रश्न

प्रश्न 1.
निम्नलिखित में से कौन सी संख्या 11 से विभाज्य है?
(a)112111
(b) 928389
(c) 12011
(d) 11111

प्रश्न 2.
कॉलम I को कॉलम II से सुमेलित कीजिए।
कॉलम I कॉलम II
(a) 11 से विभाज्य संख्या (i) 2
(b) दो क्रमागत विषम संख्याओं का HCF (ii) 4
(c) दो अभाज्य संख्याओं का अंतर (iii) संख्या का गुणनफल
(d) अभाज्य संख्या के गुणनखंडों की संख्या (iv) 60
(e) सबसे छोटी भाज्य संख्या (v)2
(f) 12 और 5 का LCM (vi) 4587594
(g) सबसे छोटी अभाज्य संख्या (vii) 1
(h) HCF और LCM का गुणनफल बराबर है (viii) 2
हल:
(a) → (vi)
(b) → (vii)
(c) → (viii) 
(d) → (i) 
(e) → (ii) 
(f) → (iv) 
(g) → (v) 

(h) → (iii)

उच्च क्रम चिंतन कौशल (HOTS)

प्रश्न 1.
बीमार गायों, 185 भेड़ों और 296 बकरियों को एक नदी पार ले जाना है। केवल एक नाव है और नाविक कहता है; वह प्रत्येक यात्रा में समान संख्या और समान प्रकार के जानवरों को ले जाएगा। प्रत्येक यात्रा में जानवरों की अधिकतम संख्या और उसे कितनी यात्राएँ करनी होंगी, ज्ञात कीजिए।
हल:
हमारे पास है
गायों की संख्या = 111
भेड़ों की संख्या = 185
बकरियों की संख्या = 296
नाविक की स्थिति के अनुसार, हमें 111, 185 और 296 का HCF ज्ञात करना है
111 = 3 x 37;
185 = 5 x 37;
296 = 2 x 2 x 2 x 37
∴ म.स.प. = 37
अतः, एक ही प्रकार के जानवरों की संख्या = 37.
यात्राओं की संख्या
= + + = 3 + 5 + 8 = 16 अतः, प्रत्येक यात्रा में जानवरों की संख्या = 37 और यात्राओं की संख्या = 16.111371853729637

प्रश्न 2.
एक सेमिनार में गणित, भौतिकी और रसायन विज्ञान में प्रतिभागियों की संख्या क्रमशः 60, 96 और 144 है। यदि प्रत्येक कमरे में समान संख्या में प्रतिभागियों को बैठाना है और वे सभी एक ही विषय में हैं, तो आवश्यक कमरों की संख्या ज्ञात कीजिए।
हल:
प्रत्येक कमरे में प्रतिभागियों की संख्या 60, 96 और 144 का HCF होना चाहिए।
∴ 60 = 2 x 2 x 3 x 5
96 = 2 x 2 x 2 x 2 x 2 x 3
144 = 2 x 2 x 2 x 2 x 3 x 3
HCF = 2 x 2 x 3 = 12
आवश्यक कमरों की संख्या
= 6012 + 9612 + 14412
= 5 + 8 + 12 = 25
अतः, प्रत्येक कमरे में प्रतिभागियों की संख्या = 12
और आवश्यक कमरों की संख्या = 25.