NCERT कक्षा 6 गणित अध्याय 11 बीजगणित
Ex 11.1
प्रश्न 1.
निम्नलिखित माचिस की तीलियों के पैटर्न बनाने के लिए आवश्यक माचिस की तीलियों की संख्या देने वाला नियम ज्ञात कीजिए। नियम लिखने के लिए एक चर का प्रयोग करें।
(a) अक्षर T का T के रूप में एक पैटर्न
(b) अक्षर Z का Z के रूप में एक पैटर्न
(c) अक्षर U का U के रूप में एक पैटर्न
(d) अक्षर V का V के रूप में एक पैटर्न
(e) अक्षर E का E के रूप में एक पैटर्न
(f) अक्षर S का S के रूप में एक पैटर्न
(g) अक्षर A का A के रूप में एक पैटर्न
हल: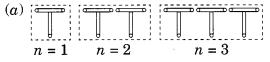
T का पैटर्न बनाने के लिए आवश्यक माचिस की तीलियों की संख्या
n = 1 के लिए 2 xn है
n = 2 के लिए 2 xn है
n = 3 के लिए xn है
∴ नियम 2n है जहाँ n T की संख्या है।
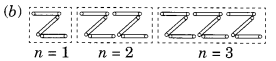
Z का पैटर्न बनाने के लिए आवश्यक माचिस की तीलियों की संख्या।
n = 1 के लिए 3 xn है।
n = 2 के लिए 3 xn है।
n = 3 के लिए 3 xn है।
∴ नियम 3n है जहाँ n Z की संख्या है।
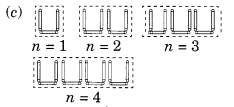
पैटर्न U बनाने के लिए आवश्यक माचिस की तीलियों की संख्या
n = 1 के लिए 3 xn है
n = 2 के लिए 3 xn है
n = 3 के लिए 3 xn है
n = 4 के लिए 3 xn है
∴ नियम 3n है जहां n Us की संख्या है।
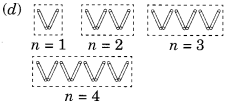
आवश्यक माचिस की संख्या
n = 1 के लिए 2 xn है
n = 2 के लिए 2 xn है
n = 3 के लिए 2 xn है
n = 4 के लिए 2 xn है
∴ नियम 2n है जहां n Vs की संख्या है।
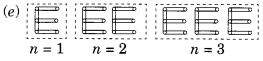
आवश्यक माचिस की संख्या
n = 1 के लिए 5 xn है
n = 2 के लिए 5 xn है
n = 3 के लिए 5 xn है
∴ नियम 5n है जहां n Es की संख्या है।
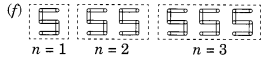
आवश्यक माचिस की संख्या
n = 1 के लिए 5 xn है
n = 2 के लिए 5 xn है
n = 3 के लिए 5 xn है
∴ नियम 5n है जहां n Ss की संख्या है।
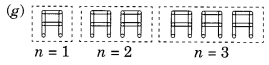
आवश्यक माचिस की संख्या
n = 1 के लिए 6 xn है
n = 2 के लिए 6 xn है
n = 3 के लिए 6 xn है
∴ नियम 6n है जहां n A की संख्या है।
प्रश्न 2.
हम पहले से ही L, C और F अक्षरों के पैटर्न के नियम को जानते हैं। Q1 के कुछ अक्षर (ऊपर दिए गए) हमें L के समान नियम देते हैं। ये कौन से हैं? ऐसा क्यों होता है?
हल:
निम्नलिखित अक्षरों के लिए नियम
L के लिए यह 2n है
C के लिए यह 2n है
V के लिए यह 2n है F के लिए यह 3n है T के लिए यह 3n है
U के लिए यह 3n है हम देखते हैं कि नियम L, V और T के लिए समान है क्योंकि उन्हें केवल 2 माचिस की तीलियों की आवश्यकता थी। अक्षर C, F और U का नियम समान है, अर्थात 3n है क्योंकि उन्हें केवल 3 तीलियों की आवश्यकता होती है।
प्रश्न 3.
कैडेट परेड में मार्च कर रहे हैं। एक पंक्ति में 5 कैडेट हैं। पंक्तियों की संख्या के लिए n का प्रयोग करें।
समाधान:
एक पंक्ति में कैडेटों की संख्या = 5
पंक्तियों की संख्या = n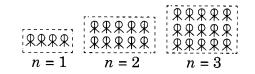
कैडेटों की संख्या
n = 1 के लिए 5 xn है
n = 2 के लिए 5 xn है
n = 3 के लिए 5 xn है
∴ नियम 5n है जहाँ n पंक्तियों की संख्या है।
प्रश्न 4.
यदि एक डिब्बे में 50 आम हैं, तो आप डिब्बों की संख्या के आधार पर आमों की कुल संख्या कैसे लिखेंगे? (डिब्बों की संख्या के लिए b का प्रयोग करें।)
हल:
डिब्बों की संख्या = b
डिब्बे में आमों की संख्या = 50
आमों की संख्या,
n = 1 के लिए 50 x b है
n = 2 के लिए 50 x b है
n = 3 के लिए 50 x b है
∴ नियम 50b है जहाँ b डिब्बों की संख्या को दर्शाता है।
प्रश्न 5.
शिक्षक प्रति छात्र 5 पेंसिल वितरित करता है। क्या आप बता सकते हैं कि छात्रों की संख्या को देखते हुए कितनी पेंसिलों की आवश्यकता है? (छात्रों की संख्या के लिए s का प्रयोग करें।)
हल:
छात्रों की संख्या = s
प्रति छात्र वितरित पेंसिलों की संख्या = 5
आवश्यक पेंसिलों की संख्या
n = 1 के लिए 5 xs है
n = 2 के लिए 5 xs है
n = 3 के लिए 5 xs है
∴ नियम 5s है जहाँ s छात्रों की संख्या को दर्शाता है।
प्रश्न 6.
एक पक्षी एक मिनट में 1 किलोमीटर उड़ता है। क्या आप पक्षी द्वारा तय की गई दूरी को मिनटों में उड़ान समय के रूप में व्यक्त कर सकते हैं? (मिनटों में उड़ान समय के लिए t का प्रयोग करें।)
हल:
1 मिनट में तय की गई दूरी = 1 किमी।
उड़ान समय = t
तय की गई दूरी
n = 1 के लिए 1 xt किमी है
n = 2 के लिए 1 xt किमी है
n = 3 के लिए 1 xt किमी है
∴ नियम 1.t किमी है जहाँ t उड़ान समय को दर्शाता है।
प्रश्न 7.
राधा एक बिंदु रंगोली (चाक पाउडर के साथ बिंदुओं को जोड़ने वाली रेखाओं का एक सुंदर पैटर्न) बना रही है। उसकी एक पंक्ति में बिंदु हैं। उसकी रंगोली में r पंक्तियों के लिए कितने बिंदु होंगे? यदि 8 पंक्तियाँ हैं तो कितने बिंदु हैं? यदि 10 पंक्तियाँ हैं?
हल:
पंक्तियों की संख्या = r
राधा द्वारा बनाई गई पंक्ति में बिंदुओं की संख्या = 8
∴ आवश्यक बिंदुओं की संख्या
r = 1 के लिए 8 xr है
r = 2 के लिए 8 xr है
r = 3 के लिए 8 xr है
∴ नियम 8r है जहाँ r पंक्तियों की संख्या का प्रतिनिधित्व करता है।
r = 8 के लिए, बिंदुओं की संख्या = 8 x 8 = 64
r = 10 के लिए, बिंदुओं की संख्या = 8 x 10 = 80
लीला राधा की छोटी बहन है। लीला राधा से 4 साल छोटी है। क्या आप लीला की उम्र राधा की उम्र के अनुसार लिख सकते हैं? राधा की उम्र x वर्ष मान लीजिए।
हल:
राधा की उम्र = x वर्ष।
दिया गया है कि लीला की उम्र
= राधा की उम्र - 4 वर्ष
= x वर्ष - 4 वर्ष
= (x - 4) वर्ष
प्रश्न 9.
माँ ने लड्डू बनाए हैं। वह कुछ लड्डू मेहमानों और परिवार के सदस्यों को देती है, फिर भी 5 लड्डू बच जाते हैं। यदि माँ द्वारा दिए गए लड्डुओं की संख्या l है, तो उसने कितने लड्डू बनाए?
हल:
दिया गया है कि दिए गए लड्डुओं की संख्या = l
शेष लड्डुओं की संख्या = 5
∴ माँ द्वारा बनाए गए लड्डुओं की संख्या = l + 5
प्रश्न 10.
संतरों को बड़े बक्सों से छोटे बक्सों में रखना है। जब एक बड़ा बक्सा खाली किया जाता है, तो उसमें से संतरे दो छोटे बक्सों को भर देते हैं और फिर भी 10 संतरे बाहर रह जाते हैं। यदि छोटे बक्से में संतरों की संख्या x मान ली जाए, तो बड़े बक्से में संतरों की संख्या क्या है?
हल:
दिया गया है कि, छोटे बक्से में संतरों की संख्या = x
∴ बड़े बक्से में संतरों की संख्या = 2(छोटे बक्से में संतरों की संख्या) + (बाहर बचे संतरों की संख्या)
अतः, बड़े बक्से में संतरों की संख्या = 2x + 10
प्रश्न 11.
(a) निम्नलिखित माचिस की तीलियों से बने वर्गों के पैटर्न को देखिए। वर्ग अलग-अलग नहीं हैं। दो पड़ोसी वर्गों में एक उभयनिष्ठ माचिस की तीली है। पैटर्न का अवलोकन कीजिए और वह नियम ज्ञात कीजिए जो वर्गों की संख्या के आधार पर माचिस की तीलियों की संख्या देता है।
(संकेत: यदि आप सिरे से खड़ी तीली हटा दें, तो आपको C का एक पैटर्न प्राप्त होगा)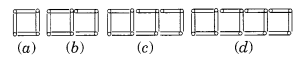
(b) निम्नलिखित आकृति त्रिभुजों का एक माचिस की तीलियों से बना पैटर्न दर्शाती है। जैसा कि ऊपर अभ्यास 11(a) में है, त्रिभुजों की संख्या के आधार पर माचिस की तीलियों की संख्या देने वाला सामान्य नियम ज्ञात कीजिए।![]()
हल:
(a) मान लीजिए वर्गों की संख्या n है।
∴ आवश्यक माचिस की तीलियों की संख्या
n = 1 के लिए 3 xn + l = 3n + 1 = 4 है
n = 2 के लिए 3 xn + l = 3n + 1 = 7 है
n = 3 के लिए 3 xn + l = 3n + 1 = 10 है
n = 4 के लिए 3 xn + l = 3n + 1 = 13 है
∴ नियम 3n + 1 है जहाँ n वर्गों की संख्या को दर्शाता है।
(b) माना त्रिभुजों की संख्या n है।
∴ आवश्यक माचिस की तीलियों की संख्या
n = 1 के
लिए 2n + 1 = 3 है n = 2 के लिए 2n + 1 = 5 है
n = 3 के लिए 2n + 1 = 7
है n = 4 के लिए 2n + 1 = 9 है
∴ नियम 2n + 1 है जहाँ n माचिस की तीलियों की संख्या को दर्शाता है।
Ex 11.2
प्रश्न 1.
एक समबाहु त्रिभुज की भुजा l द्वारा दर्शाई गई है। l का उपयोग करके समबाहु त्रिभुज का परिमाप व्यक्त कीजिए।
हल:
दिया गया है कि समबाहु त्रिभुज की भुजा = l
समबाहु त्रिभुज का परिमाप = 3 x भुजा = 3 x l = 3 l इकाई
प्रश्न 2.
एक सम षट्भुज (चित्र देखें) की भुजा l द्वारा निरूपित की जाती है। l का उपयोग करके षट्भुज का परिमाप व्यक्त करें।
(संकेत: एक सम षट्भुज की सभी छह भुजाएँ लंबाई में समान होती हैं)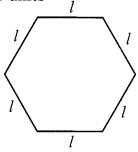
हल:
दिया गया है कि षट्भुज की प्रत्येक भुजा = l
∴ सम षट्भुज का परिमाप = l + l + l + l + l + l
= 6 xl = 6 l इकाई
प्रश्न 3.
एक घन एक त्रि-विमीय आकृति है जैसा कि आकृति में दिखाया गया है। इसके छह फलक हैं और ये सभी समान वर्ग हैं। घन के एक किनारे की लंबाई l है। घन के किनारों की कुल लंबाई का सूत्र ज्ञात कीजिए।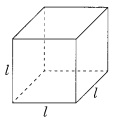
हल:
हम जानते हैं कि एक घन में 12 किनारे और 6 समान फलक होते हैं।
चूँकि सभी किनारे समान लंबाई के होते हैं।
∴ किनारों की कुल लंबाई = 12 x l = 12 l इकाई
∴ अभीष्ट सूत्र = 12 l इकाई
प्रश्न 4.
एक वृत्त का व्यास एक रेखा है जो वृत्त पर स्थित दो बिंदुओं को मिलाती है और वृत्त के केंद्र से भी होकर जाती है। (संलग्न आकृति में, AB वृत्त का व्यास है; C इसका केंद्र है)। वृत्त के व्यास (d) को उसकी त्रिज्या (r) के पदों में व्यक्त कीजिए।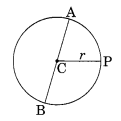
हल:
दिया गया है: त्रिज्या = r और व्यास = d
∴ व्यास = 2 x त्रिज्या = 2 x r = 2r
अतः, व्यास = 2r.
प्रश्न 5.
तीन संख्याओं 14, 27 और 13 का योग ज्ञात करने के हमारे पास दो तरीके हैं;
(a) हम पहले 14 और 27 को जोड़कर 41 प्राप्त कर सकते हैं और फिर इसमें 13 जोड़कर कुल योग 54 प्राप्त कर सकते हैं या
(b) हम 27 और 13 को जोड़कर 13 जोड़कर 40 प्राप्त कर सकते हैं और फिर इसमें 14 जोड़कर योग 54 प्राप्त कर सकते हैं।
इस प्रकार, (14 + 27) + 13 = 14 + (27 + 13)
यह किसी भी तीन संख्याओं के लिए किया जा सकता है। इस गुण को संख्याओं के योग की साहचर्यता के रूप में जाना जाता है। इस गुण को, जिसका अध्ययन हम पूर्ण संख्याओं वाले अध्याय में कर चुके हैं, सामान्य रूप से a, b और c का उपयोग करके व्यक्त करें।
हल:
तीन संख्याएँ a, b और c दी गई हैं।
संख्याओं के योग का साहचर्य गुण = (a + b) + c = a + (b + c)
Ex 11.3
प्रश्न 1.
तीन संख्याओं 5, 7 और 8 से जितने हो सके उतने संख्याओं वाले व्यंजक (बिना चर वाले) बनाइए। प्रत्येक संख्या का प्रयोग एक से अधिक बार नहीं होना चाहिए। केवल जोड़, घटाव और गुणा का प्रयोग कीजिए।
हल:
दी गई संख्याएँ 5, 7 और 8 हैं।
व्यंजक हैं:
(i) 8 + (5 + 7)
(ii) 5 + (8 – 7)
(iii) 8 + (5 x 7)
(iv) 7 – (8 – 5)
(v) 7 x (8 + 5)
(vi) 5 x (8 + 7)
(vii) 8 x (5 + 7)
(viii) 7 + (8 – 5)
(ix) (5 x 7) – 8
(x) 7 + (8 x 5)
प्रश्न 2.
निम्नलिखित में से कौन से केवल संख्याओं वाले व्यंजक हैं?
(a) y + 3
(b) (7 x 20) – 8z
(c) 5(21 – 7) + 7 x 2
(d) 5
(e) 3x
(f) 5 – 5n
(g) (7 x 20) – (5 x 10) – 45 +p
हल:
(a) y + 3. इस व्यंजक में चर 'y' है।
(b) (7 x 20) – 8z. इस व्यंजक में चर 'z' है।
(c) 5(21 -7) + 7 x 2. इस व्यंजक में कोई चर नहीं है। तो यह केवल संख्याओं के साथ है।
(d) 5. यह व्यंजक केवल संख्याओं के साथ है।
(e) 3x. इस व्यंजक में चर 'x' है।
(f) 5 – 5n. इस व्यंजक में चर 'n' है।
(g) (7 x 20) – (5 x 10) – 45 + p. इस व्यंजक में एक चर 'p' है।
प्रश्न 3.
निम्नलिखित व्यंजकों को बनाने में प्रयुक्त संक्रियाओं (जोड़, घटाव, भाग और गुणा) को पहचानिए और बताइए कि व्यंजक किस प्रकार बनाए गए हैं।
(a) z + 1, z – 1,y + 17, y – 17
(b) 17y,
(c) 2y + 17, 2y – 17
(d) 7m, -7m + 3, -7m – 3
हल:
| Expressions | Operations used | Formation of expression | ||
| (a) | (i) | z + 1 | Addition | z is increased by 1 |
| (ii) | z – 1 | Subtraction | z is decreased by 1 | |
| (iii) | y +17 | Addition | y is increased by 17 | |
| (iv) | y -17 | Subtraction | y is decreased by 17 | |
| (b) | (i) | 17y | Multiplication | y is multiplied by 17 |
| (ii) | y/17 | Division | y is Divided by 17 | |
| (iii) | 5z | Multiplication | z is Multiplied by 5 | |
| (c) | (i) | 2y + 17 | Multiplication and addition | y is multiplied by 2 and then 17 is added. |
| (ii) | 2y -17 | Multiplication and subtraction | Twice of y is decreased by 17 | |
| (d) | (i) | 7 m | Multiplication | m is multiplied by 7 |
| (ii)- | -7m + 3 | Multiplication and addition | m is multiplied by -7 and then increased by 3 | |
| (iii) | -7m – 3 | Multiplication and subtraction | M is multiplied by -7 and then decreased by 3 | |
प्रश्न 4.
निम्नलिखित के लिए व्यंजक दीजिए:
(a) 7 जोड़ा गया
(b) 7 घटाया गया p से
(c) p को 7 से गुणा किया गया
(d) p को 7 से भाग दिया गया
(e) 7 घटाया गया -m से
(j) -p को 5 से गुणा किया गया
(g) -p को 5 से भाग दिया गया
(h) p को -5 से गुणा किया गया
हल:
(a) p + 7
(b) p – 7
(c) 7p
(d) \(\frac { p }{ 7 }\)
(ई) -एम – 7
(एफ) -5पी
(जी) \(\frac { -पी }{ 5 }\)
(एच) 5पी
प्रश्न 5.
निम्नलिखित स्थितियों में व्यंजक दीजिए:
(a).2m में 11 जोड़ा गया
(b) 2m में से 11 घटाया गया
(c) y का 5 गुना जिसमें 3 जोड़ा गया
(d) y का 5 गुना जिसमें से 3 घटाया गया
(e) y को -8 से गुणा किया गया
(f) y को -8 से गुणा किया गया और फिर परिणाम में 5 जोड़ा गया
(g) y को 5 से गुणा किया गया और परिणाम में से 16 घटाया गया
हल:
(a) 2m + 11
(b) 2m – 11
(e) 5y + 3
(d) 5y – 3
(e) -8y
(f) -8y+5
(g) 16 – 5y
(h) -5y + 16
प्रश्न 6.
(a) t और 4 का उपयोग करके व्यंजक बनाएँ। एक से अधिक संख्या संक्रिया का प्रयोग न करें। प्रत्येक व्यंजक में t अवश्य होना चाहिए।
(b) y, 2 और 7 का उपयोग करके व्यंजक बनाएँ। प्रत्येक व्यंजक में y अवश्य होना चाहिए। केवल दो संख्या संक्रियाओं का प्रयोग करें। ये भिन्न होनी चाहिए।
हल:
(a) संभावित व्यंजक हैं:
(i) t + 4
(ii) t – 4
(iii) 4t
(iv) \(\frac { t }{ 4 }\)
(v) 4 + टी
(vi) 4 + टी, आदि।
(b) संभावित व्यंजक हैं:
(i) 2y + 7
(ii) 7y – 2
(iii) 7 – 2y
(iv) 7y + 2
(v) \(\frac { 7y }{ 2 }\)
(vi) \(\frac { 2y }{ 7 }\)
(vii) \(\frac { y }{ 7 }\) + 2
(viii) \(\frac { y }{ 2 }\) - 7,आदि।
Ex 11.4
प्रश्न 1.
निम्नलिखित के उत्तर दीजिए:
(a) सरिता की वर्तमान आयु को 5 वर्ष लें।
(i) अब से 5 वर्ष बाद उसकी आयु क्या होगी?
(ii) 3 वर्ष पहले उसकी आयु क्या थी?
(iii) सरिता के दादा की आयु उसकी आयु की 6 गुनी है। उसके दादा की आयु क्या है?
(iv) दादी, दादा से 2 वर्ष छोटी हैं। दादी की आयु क्या है?
(v) सरिता के पिता की आयु सरिता की आयु के 3 गुने से 5 वर्ष अधिक है। उसके पिता की आयु क्या है?
(b) एक आयताकार हॉल की लंबाई हॉल की चौड़ाई के 3 गुने से 4 मीटर कम है। यदि चौड़ाई b मीटर है, तो लंबाई क्या है?
(c) एक आयताकार बॉक्स की ऊँचाई h सेमी है। इसकी लंबाई ऊँचाई की 5 गुनी है और चौड़ाई लंबाई से 10 सेमी कम है। बॉक्स की लंबाई और चौड़ाई को ऊँचाई के रूप में व्यक्त कीजिए।
(d) मीना, बीना और लीना पहाड़ी की चोटी पर जाने के लिए सीढ़ियाँ चढ़ रही हैं। मीना सीढ़ी s पर है, बीना 8 कदम आगे है और लीना 7 कदम पीछे है। बीना और मीना कहाँ हैं? पहाड़ी की चोटी तक जाने के लिए सीढ़ियों की कुल संख्या मीना द्वारा पहुँची गई सीढ़ियों की संख्या के 4 गुने से 10 कम है। सीढ़ियों की कुल संख्या को s का प्रयोग करके व्यक्त कीजिए।
(e) एक बस v किमी प्रति घंटे की चाल से चलती है। यह दासपुर से बीसपुर जा रही है। बस के 5 घंटे चलने के बाद भी बीसपुर 20 किमी दूर है। दासपुर से बीसपुर की दूरी कितनी है? इसे v का प्रयोग करके व्यक्त कीजिए।
हल:
(a) सरिता की आयु y वर्ष दी गई है।
(i) अब से 5 वर्ष बाद उसकी आयु (y + 5) वर्ष होगी।
(ii) अब से 3 वर्ष पहले
उसकी आयु (y – 3) वर्ष थी।
(iii) उसके दादा की आयु = 6y वर्ष
(b) माना आयताकार हॉल की लंबाई T है
∴ लंबाई = (3b – 4) मीटर
जहाँ b चौड़ाई को दर्शाता है।
(c) आयताकार बॉक्स की ऊँचाई 'h' है
∴ लंबाई = 5h सेमी
और चौड़ाई = (5h - 10) सेमी.
(d) मीना सीढ़ी s पर है।
∴ बीना (s + 8) सीढ़ियों पर है और लीना (s – 7) सीढ़ियों पर है।
पहाड़ी की चोटी पर जाने के लिए कुल सीढ़ियों की संख्या = (4s – 10)
(e) बस द्वारा 5 घंटे में तय की गई दूरी = 5v किमी.
∴ दासपुर से बीसपुर की दूरी = (5v + 20) किमी.
प्रश्न 2.
व्यंजकों का प्रयोग करते हुए निम्नलिखित कथनों को सामान्य भाषा के कथनों में बदलें।
(उदाहरण के लिए, दिया गया है कि सलीम ने क्रिकेट मैच में r रन बनाए, नलिन ने (r + 15) रन बनाए। साधारण भाषा में - नलिन ने सलीम से 15 रन अधिक बनाए।
(a) एक नोटबुक की कीमत ₹p है। एक किताब की कीमत ₹3p है।
(b) टोनी ने मेज पर q कंचे रखे। उसके बॉक्स में 8q कंचे हैं।
(c) हमारी कक्षा में n छात्र हैं। स्कूल में 20n छात्र हैं।
(d) जग्गू 2 वर्ष का है। उसके चाचा 42 वर्ष के हैं और उसकी चाची (4z - 3) वर्ष की हैं।
(e) बिंदुओं की व्यवस्था में r पंक्तियाँ हैं। प्रत्येक पंक्ति में 5 बिंदु हैं।
हल:
(a) एक किताब की कीमत नोटबुक की कीमत की 3 गुनी है। (b) टोनी
के पास मेज पर रखे कंचों की संख्या उसकी आयु उसके चाचा की आयु से 3 वर्ष कम है। (e) एक पंक्ति में बिंदुओं की संख्या पंक्तियों की संख्या की 5 गुनी है।
प्रश्न 3.
(a) मन्नू की आयु x वर्ष दी गई है। क्या आप अनुमान लगा सकते हैं कि (x – 2) क्या दर्शाएगा?
(संकेत: मन्नू के छोटे भाई के बारे में सोचें) क्या आप अनुमान लगा सकते हैं कि (x + 4) अब क्या दर्शाएगा? (3x + 7) क्या दर्शाएगा?
(b) सारा की आज की आयु x वर्ष दी गई है। भविष्य में या अतीत में उसकी आयु के बारे में सोचें।
निम्नलिखित व्यंजक क्या दर्शाएगा?
y + 7, y – 3, y + 4 \(\frac { 1 }{ 2 }\) , y – 2 \(\frac { 1 }{ 2 }\) . (c) दिया गया है कि कक्षा में n विद्यार्थी फुटबॉल पसंद करते हैं, 2n क्या दर्शा सकता है? \(\frac { n }{ 2 }\) क्या दर्शा सकता है? (फुटबॉल के अलावा अन्य खेलों के बारे में सोचें)। हल: (a) दिया गया है कि मन्नू की आयु = x वर्ष। ∴ (x -2) वर्ष उसके छोटे भाई या छोटी बहन की आयु हो सकती है। (x + 4) वर्ष उसके बड़े भाई या बड़ी बहन की आयु दर्शाता है। (3x + 7) वर्ष उसके पिता, माता या चाचा की आयु हो सकती है।
(b) y सारा की आयु को वर्षों में दर्शाता है।
∴ y + 7 उसकी भावी आयु दर्शाता है।
y – 3 उसकी पिछली आयु दर्शाता है। y + 4 \(\frac { 1 }{ 2 }\) उसकी भावी आयु दर्शाता है, अर्थात z के साढ़े चार वर्ष
बाद की आयु । y – 2 \(\frac { 1 }{ 2 }\) उसकी पिछली आयु दर्शाता है, अर्थात z के ढाई वर्ष पहले की आयु।
(c) फुटबॉल पसंद करने वाले छात्रों की संख्या = n
∴ 2n = फुटबॉल खिलाड़ियों की संख्या का दोगुना क्रिकेट खेलना पसंद कर सकते हैं।
और \(\frac { n }{ 2 }\) = फुटबॉल खिलाड़ियों की संख्या का आधा 2 खिलाड़ी बास्केटबॉल खेलना पसंद कर सकते हैं।
Ex 11.5
प्रश्न 1.
बताइए कि निम्नलिखित में से कौन-से समीकरण (चर सहित) हैं। अपने उत्तर का कारण बताइए। चर सहित समीकरणों में से चर की पहचान कीजिए।
(a) 17 = x + 7
(b) (t – 7) > 5
(c)
(d) (7 x 3) – 19 = 8
(e) 5 x 4 – 8 = 2x
(f) x -2 = 0
(g) 2m < 30
(h) 2n + 1 = 11
(i) 7 = (11 x 5) – (12 x 4)
(j) 7 = (11 x 2) + p
(k) 20 = 5y
(l)
(n) 20 – (10 – 5) = 3 x 5
(o) 7 – x = 5
हल:
(a) 17 = x + 7 एक चर x वाला समीकरण है।
(b) (t – 7) > 5 एक समीकरण नहीं है क्योंकि इसमें '=' चिह्न नहीं है।
(c)
(d) (7 x 3) – 19 = 8 एक समीकरण नहीं है क्योंकि इसमें कोई चर नहीं है।
(e) 5 x 4 – 8 = 2x एक समीकरण है जिसमें x चर है।
(f) x – 2 = 0 एक समीकरण है जिसमें x चर है।
(g) 2m < 30 एक समीकरण नहीं है क्योंकि इसमें '=' चिह्न नहीं है।
(h) 2n + 1 = 11 एक समीकरण है जिसमें n चर है।
(i) 7 = (11 x 5) – (12 x 4) एक समीकरण नहीं है क्योंकि इसमें कोई चर नहीं है।
(j) 7 = (11 x 2) + p एक समीकरण है जिसमें p चर है।
(k) 20 = 5y एक समीकरण है जिसमें y चर है।
(l)
(n) 20 – (10 – 5) = 3 x 5 एक समीकरण नहीं है क्योंकि इसमें कोई चर नहीं है।
(o) 7 – x = 5 एक समीकरण है जिसमें एक चर x है।
प्रश्न 2.
तालिका के तीसरे कॉलम में प्रविष्टियों को पूरा करें।
| S. No. | Equation | Value of variable | Equations satisfied Yes /No |
| (a) | 10y = 80 | y = 10 | |
| (b) | 10y = 80 | y = 8 | |
| (c) | 10y = 80 | y = 5 | |
| (d) | 4l = 20 | l = 20 | |
| (e) | 4l = 20 | l = 80 | |
| (f) | 4l = 20 | l = 5 | |
| (g) | b + 5 = 9 | b = 5 | |
| (h) | b + 5 = 9 | b = 9 | |
| (i) | b + 5 = 9 | b = 4 | |
| (J) | h – 8 = 5 | h = 13 | |
| (k) | h – 8 = 5 | h = 8 | |
| (l) | h – 8 = 5 | h = 0 | |
| (m) | P + 3 = 1 | p = 3 | |
| (n) | p + 3 = 1 | p = 1 | |
| (o) | p + 3 = 1 | p = 0 | |
| (P) | p + 3 = 1 | p = -1 | |
| (q) | p + 3 = 1 | p = -2 |
समाधान:
| S. No. | Equation | Value of variable | Equations satisfied Yes /No |
| (a) | 10y = 80 | y = 10 | No |
| (b) | 10y = 80 | y = 8 | Yes |
| (c) | 10y = 80 | y = 5 | No |
| (d) | 4l = 20 | l = 20 | No |
| (e) | 4l = 20 | l = 80 | No |
| (f) | 4l = 20 | l = 5 | Yes |
| (g) | b + 5 = 9 | b = 5 | No |
| (h) | b + 5 = 9 | b = 9 | No |
| (i) | b + 5 = 9 | b = 4 | Yes |
| (J) | h – 8 = 5 | h = 13 | Yes |
| (k) | h – 8 = 5 | h = 8 | No |
| (l) | h – 8 = 5 | h = 0 | No |
| (m) | P + 3 = 1 | p = 3 | No |
| (n) | p + 3 = 1 | p = 1 | No |
| (o) | p + 3 = 1 | p = 0 | No |
| (P) | p + 3 = 1 | p = -1 | No |
| (q) | p + 3 = 1 | p = -2 | Yes |
प्रश्न 3.
प्रत्येक समीकरण के आगे कोष्ठक में दिए गए मानों में से हल चुनिए। दर्शाइए कि अन्य मान समीकरण को संतुष्ट नहीं करते हैं।
(a) 5m = 60 (10, 5, 12, 15)
(b) n + 12 = 20 (12, 8, 20, 0)
(c) p – 5 = 5 (0, 10, 5, -5)
(d)
(e) r – 4 = 0 (4, -4, 8, 0)
(f) x + 4 = 2 (-2, 0, 2, 4)
हल:
(a) m = 10 के लिए, बायाँ पक्ष = 5 x 10 = 50, दायाँ पक्ष = 60
यहाँ, बायाँ पक्ष ≠ दायाँ पक्ष
∴ m = 10 समीकरण का हल नहीं है
m = 5 के लिए, बायाँ पक्ष = 5×5 = 25, दायाँ पक्ष = 60
यहाँ, बायाँ पक्ष ≠ दायाँ पक्ष
∴ m = 5 समीकरण का हल नहीं है
m = 12 के लिए, बायाँ पक्ष = 5 x 12 = 60, दायाँ पक्ष = 60
यहाँ, बायाँ पक्ष = दायाँ पक्ष
∴ m = 12 समीकरण का हल है
m = 15 के लिए बायाँ पक्ष = 5 x 15 = 75, दायाँ पक्ष = 60
यहाँ, बायाँ पक्ष ≠ दायाँ पक्ष
∴ m = 15 समीकरण का हल नहीं है
(b) n + 12 = 20 (12, 8, 20, 0)
n = 12 के लिए, बायाँ पक्ष = 12 + 12 = 24, दायाँ पक्ष = 20
यहाँ, बायाँ पक्ष ≠ दायाँ पक्ष
∴ n = 12 समीकरण का हल नहीं है
n = 8 के लिए, बायाँ पक्ष = 8 + 12 = 20, दायाँ पक्ष = 20
यहाँ, बायाँ पक्ष = दायाँ पक्ष
∴ n = 8 समीकरण का हल है
n = 20 के लिए, बायाँ पक्ष = 20 + 12 = 32, दायाँ पक्ष = 20
यहाँ, बायाँ पक्ष ≠ दायाँ पक्ष
∴ n = 20 समीकरण का हल नहीं है
n = 0 के लिए, बायाँ पक्ष = 0 + 12 – 12, दायाँ पक्ष = 20
यहाँ, बायाँ पक्ष ≠ दायाँ पक्ष
∴ n= 0 समीकरण का हल नहीं है
(c) p – 5 = 5 (0, 10, 5, -5)
p = 0 के लिए, बायाँ पक्ष = 0 – 5 = -5, दायाँ पक्ष = 5
यहाँ, बायाँ पक्ष ≠ दायाँ पक्ष
∴ p = 0 समीकरण का हल नहीं है
p = 10 के लिए, बायाँ पक्ष = 10 – 5 = 5, दायाँ पक्ष = 5
यहाँ, बायाँ पक्ष = दायाँ पक्ष
∴ p = 10 समीकरण का हल है
p = 5 के लिए, बायाँ पक्ष = 5-5-0, दायाँ पक्ष = 5
यहाँ, बायाँ पक्ष ≠ दायाँ पक्ष
∴ p = 5 समीकरण का हल नहीं है
p = 5 के लिए, बायाँ पक्ष = 5 – 5 = 0, दायाँ पक्ष = 5
यहाँ, बायाँ पक्ष ≠ दायाँ पक्ष
∴ p = -5 समीकरण का हल नहीं है
(d)
q = 7 के लिए, बायाँ पक्ष =
यहाँ LHS ≠ RHS
∴ q = 7 समीकरण का हल नहीं है
q = 2 के लिए, LHS =
यहाँ, बायाँ पक्ष ≠ दायाँ पक्ष
∴ q = 2 समीकरण का हल नहीं है
q = 10 के लिए, बायाँ पक्ष =
यहाँ, बायाँ पक्ष ≠ दायाँ पक्ष
q = 14 के लिए, बायाँ पक्ष =
यहाँ, बायाँ पक्ष = दायाँ पक्ष
∴ q = 14 समीकरण का हल है
(e) r – 4 = 0 (4, -4, 8, 0)
r = 4 के लिए, बायाँ पक्ष = 4 – 4 = 0, दायाँ पक्ष = 0
यहाँ, बायाँ पक्ष = दायाँ पक्ष
∴ r = 4 समीकरण का हल है
r = -4 के लिए, बायाँ पक्ष = -4 – 4 = -8, दायाँ पक्ष = 0
यहाँ, बायाँ पक्ष ≠ दायाँ पक्ष
∴ r = -4 समीकरण का हल नहीं है
r = 8 के लिए, बायाँ पक्ष = 8 – 4 = 4, दायाँ पक्ष = 0
यहाँ, बायाँ पक्ष ≠ दायाँ पक्ष
r = 8 के लिए समीकरण का हल नहीं है
r = 0 के लिए, बायाँ पक्ष = 0 – 4 = – 4, दायाँ पक्ष = 0
यहाँ, बायाँ पक्ष ≠ दायाँ पक्ष
∴ r = 0 समीकरण का हल नहीं है
(f) x + 4 = 2 (-2, 0, 2, 4)
x = -2 के लिए, बायाँ पक्ष = -2 + 4 = 2, दायाँ पक्ष = 2
यहाँ, बायाँ पक्ष – दायाँ पक्ष
∴ x = -2 समीकरण का हल है
x = 0 के लिए, बायाँ पक्ष = 0 + 4 – 4, दायाँ पक्ष = 2
यहाँ, बायाँ पक्ष ≠ दायाँ पक्ष
∴ x = 0 समीकरण का हल नहीं है
x = – 2 के लिए, बायाँ पक्ष = -2 + 4 – 6, दायाँ पक्ष = 2
यहाँ, बायाँ पक्ष ≠ दायाँ पक्ष
∴ x = 2 समीकरण का हल नहीं है
r = 4 के लिए, बायाँ पक्ष = 4 + 4 = 8, दायाँ पक्ष = 2
यहाँ, बायाँ पक्ष ≠ दायाँ पक्ष
∴ x = 4 समीकरण का हल नहीं है
प्रश्न 4.
(a) तालिका को पूरा करें और तालिका का निरीक्षण करके समीकरण m + 10 = 6 का हल ज्ञात करें।
(b) तालिका को पूरा करें और तालिका का निरीक्षण करके समीकरण 51 – 35 का हल ज्ञात करें।
(c) तालिका को पूरा करें और तालिका का उपयोग करके समीकरण g = 4 का हल ज्ञात करें।
(d) तालिका को पूरा करें और समीकरण m – 7 = 3 का हल ज्ञात करें।
हल:
(a) निरीक्षण से, हमें प्राप्त हुआ है
इसलिए, m – 6 समीकरण का हल है।
(b) दिया गया है कि 5t = 35
अतः, t = 7 समीकरण का हल है।
(c) दिया गया है कि
अतः z = 12 समीकरण का हल है।
(d) दिया गया है कि m – 7 = 3
अतः, m = 10 समीकरण का हल है।
प्रश्न 5.
निम्नलिखित पहेलियों को हल कीजिए, आप स्वयं भी ऐसी पहेलियाँ बना सकते हैं। मैं कौन हूँ?
(i) एक वर्ग के चारों ओर घूमिए और
हर कोने को
तीन बार गिनिए, इससे ज़्यादा नहीं!
मुझे गिनती में जोड़िए,
ठीक चौंतीस पाने के लिए!
(ii) सप्ताह के प्रत्येक दिन के लिए
मुझसे गिनती करो
यदि आप कोई गलती नहीं करते हैं तो
आपको तेईस मिलेंगे!
(iii) मैं एक ख़ास नंबर हूँ,
मुझसे एक छक्का छीन लो!
एक पूरी क्रिकेट टीम को
तुम फिर भी ठीक कर पाओगे!
(iv) मुझे बताओ मैं कौन हूँ
मैं तुम्हें एक अच्छा सुराग दूंगा!
तुम मुझे वापस पा लोगे
अगर तुम मुझे बाईस में से निकाल दो!
हल:
(i) शर्त के अनुसार,
I + 12 = 34 या x + 12 = 34
∴ निरीक्षण से, हमारे पास
22 + 12 = 34 है
इसलिए, मैं 22 हूँ।
(ii) मान लीजिए I, 'x' है।
हम जानते हैं कि एक सप्ताह में 7 दिन होते हैं।
∴ x से 7 तक गिनने पर, योग = 23 है।
निरीक्षण करने पर, हमें
16 + 7 = 23 प्राप्त होता है।
∴ x = 16
है। अतः I, 16 है।
(iii) माना विशेष संख्या x है और क्रिकेट टीम में 11 खिलाड़ी हैं।
∴ विशेष संख्या -6 = 11
∴ x – 6 = 11
निरीक्षण करने पर, हम पाते हैं
17 – 6 = 11
∴ x = 17
अतः मैं 17 हूँ।
(iv) मान लीजिए I 'x' है।
∴ 22 – I = I
या 22 – x = x
निरीक्षण से, हमें प्राप्त होता है
22 – 11 = 11
∴ x = 11
इस प्रकार I 11 है।
InText Questions
लघु उत्तरीय प्रश्न
प्रश्न 1.
एक नियमित षट्भुज की भुजा s सेमी है। इसका परिमाप ज्ञात कीजिए।
हल:
एक नियमित षट्भुज की प्रत्येक भुजा = s
∴ इसका परिमाप = s + s + s + s + s = 6s सेमी
प्रश्न 2. तालिका को पूरा करें और समीकरण 19 – x = 13 का हल ज्ञात कीजिए हल: निरीक्षण से, हमें मिलता है इस प्रकार, आवश्यक समाधान 6 है।12 and c = 14 , find the value of
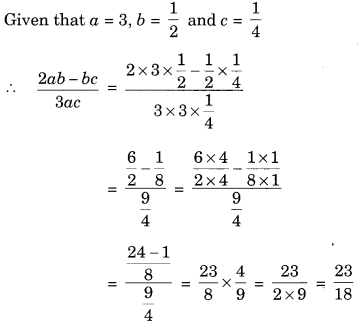


प्रश्न 3.
यदि x = –\(\frac { 1 }{ 2 }\), y = \(\frac { 1 }{ 4 }\) और z = 0, दिए गए व्यंजकों का मान ज्ञात कीजिए (a) 8z + 2x -y (b) z – y + 3x हल: प्रश्न 15. रिक्त स्थान भरें: (a) -5 में 5 जोड़ने पर = ………. (b) यदि x = 3, तो 3x – 5 = ………. (c) यदि x = 1 और y = 2, तो 2x + 3y = ………. (d) यदि 10x – 6 = 14, तो x = ………. (e) किसी संख्या से 4 कम x = ………. हल: (a) 0 (b) 4 (c) 8 (d) 2 (e) x – 412 , y = 14 and z = 0, find the value of the given expressions
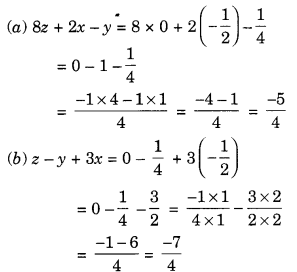
एक नियमित षट्भुज की भुजा s सेमी है। इसका परिमाप ज्ञात कीजिए।
हल:
एक नियमित षट्भुज की प्रत्येक भुजा = s
∴ इसका परिमाप = s + s + s + s + s = 6s सेमी

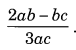
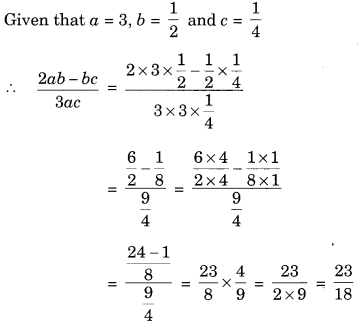


यदि x = –\(\frac { 1 }{ 2 }\), y = \(\frac { 1 }{ 4 }\) और z = 0, दिए गए व्यंजकों का मान ज्ञात कीजिए (a) 8z + 2x -y (b) z – y + 3x हल: प्रश्न 15. रिक्त स्थान भरें: (a) -5 में 5 जोड़ने पर = ………. (b) यदि x = 3, तो 3x – 5 = ………. (c) यदि x = 1 और y = 2, तो 2x + 3y = ………. (d) यदि 10x – 6 = 14, तो x = ………. (e) किसी संख्या से 4 कम x = ………. हल: (a) 0 (b) 4 (c) 8 (d) 2 (e) x – 4
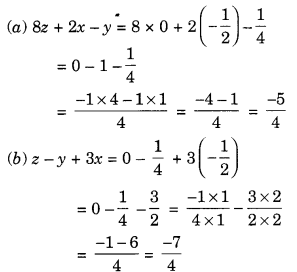
अति लघु उत्तरीय प्रश्न
प्रश्न 1.
किसी संख्या से छह कम होने पर दो आते हैं। वह संख्या क्या है?
हल:
मान लीजिए संख्या 'x' है।
शर्त के अनुसार, x – 6 = 2 है।
जाँच करने पर, 8 – 6 = 2 है।
∴ x = 8 है।
अतः, अभीष्ट संख्या 8 है।
प्रश्न 2.
निम्नलिखित में से प्रत्येक के लिए एक बीजीय व्यंजक लिखिए:
(a) एक संख्या y में से 3 घटाया जाता है।
(b) एक संख्या x के तीन गुने में 5 जोड़ा जाता है।
हल:
(a) अभीष्ट व्यंजक y – 3 है।
(b) अभीष्ट व्यंजक 5 + 3x है।
प्रश्न 3.
निम्नलिखित व्यंजकों के लिए एक बीजीय व्यंजक लिखिए:
(a) एक संख्या x और 4 का योग दोगुना कर दिया जाता है।
(b) एक संख्या x का एक-चौथाई उसी संख्या के एक-तिहाई में जोड़ दिया जाता है।
हल:
(a) अभीष्ट व्यंजक 2x (x + 4) है।
(b) अभीष्ट व्यंजक \(\frac { 1 }{ 4 }\)x + \(\frac { 1 }{ 3 }\)x है।
प्रश्न 4.
एक संख्या x पर विचार कीजिए। इसे 3 से गुणा कीजिए और गुणनफल में 5 जोड़कर y घटाइए। परिणामी संख्या ज्ञात कीजिए।
हल:
अभीष्ट संख्या (3x + 5) है।
अब हमें परिणाम में से y घटाना है, अर्थात् 3x + 5 – y
प्रश्न 5.
यहाँ माचिस की तीलियों से बने घरों का एक पैटर्न दिया गया है: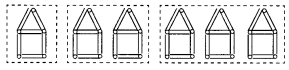
इस पैटर्न का सामान्य नियम लिखिए।
हल:
एक घर 6 माचिस की तीलियों से बना है अर्थात 6 x 1
दो घर 12 माचिस की तीलियों से बने हैं अर्थात 6 x 2
तीन घर 18 माचिस की तीलियों से बने हैं अर्थात 6 x 3
∴ नियम 6n है जहाँ n घरों की संख्या दर्शाता है।
प्रश्न 6.
यदि एक समबाहु त्रिभुज की भुजा x है, तो उसका परिमाप ज्ञात कीजिए।
हल:
हम जानते हैं कि एक समबाहु त्रिभुज की तीनों भुजाएँ बराबर होती हैं।
∴ x + x + x = 3x।
अतः, अभीष्ट परिमाप = 3x इकाई है।
प्रश्न 7.
यदि x = 3 है, तो निम्नलिखित का मान ज्ञात कीजिए:
(i) x + 5
(ii) 2x – 3
(iii) x – 7
(iv) \(\frac { x }{ 3 }\) – 1 हल: दिया गया है कि x = 3 (i)x + 5 = 3 + 5 = 8 (ii) 2x – 3 = 2 x 3 – 3 = 6 – 3 = 3 (iii) x – 7 = 3- 7 = -4 (iv) \(\frac { x }{ 3 }\) – 1 = \(\frac { 3 }{ 3 }\) -1 = 1 – 1 = 0
प्रश्न 8.
यदि x = 2, y = 3 और 2 = 5, तो निम्न का मान ज्ञात कीजिए;
(a) 2x + y + z
(b) 4x -y + z
(c) x – y + z
हल:
(a) दिया गया है: x – 2, y = 3 और z = 5
∴ 2x + y + 2 = 2 x 2 + 3 + 5
= 4 + 3 + 5 = 12
(b) 4x – y + z = 4 x 2 – 3 + 5
= 8 – 3 + 5 = 5 + 5 = 10
(c) x – y + z = 2 – 3 + 5 = -1 + 5 = 4
प्रश्न 9.
बताइए निम्नलिखित में से कौन से समीकरण चर वाले हैं?
(a) 12 = x – 5
(b) 2x > 7
(c) \(\frac { x }{ 2 }\) = 5 (d) 5 + 7 = 3 + 9 (e) 7 = (11 x 5) – (12 x 4) हल: (a) 12 = x – 5 एक समीकरण है जिसमें चर x है। (b) 2x > 7 एक समीकरण नहीं है क्योंकि इसमें '=' चिह्न नहीं है।
(c) \(\frac { x }{ 2 }\) = 5 एक समीकरण है जिसमें x चर है। (d) 5 + 7 = 3 + 9 एक समीकरण नहीं है क्योंकि इसमें कोई चर नहीं है।
(e) 7 = (11 x 5) – (12 x 4) एक समीकरण नहीं है क्योंकि इसमें कोई चर नहीं है।
प्रश्न 10.
एक संख्या सोचें, उसमें 2 जोड़ें और फिर योग को 6 से गुणा करें, परिणाम 42 है।
हल:
माना संख्या x है।
∴ x और 2 का योग = x + 2
अब योग को 6 से गुणा करके, हम पाते हैं
6 × (x + 2) = 42
⇒ 6 × x + 6 × 2 = 42
⇒ 6x + 12 = 42
निरीक्षण करके, हम पाते हैं
6 × 5 + 12 = 42
⇒ 30 + 12 = 42
∴ 42 = 42
तो, अभीष्ट संख्या = 5
उच्च क्रम चिंतन कौशल (HOTS)
प्रश्न 1.
A सुबह 6 बजे दिल्ली से अमृतसर के लिए अपनी कार शुरू करता है। उसकी कार की एकसमान गति x किमी/घंटा है। दोपहर 12 बजे, वह पाता है कि वह अभी भी अमृतसर से 50 किमी दूर है। दिल्ली और अमृतसर के बीच की दूरी ज्ञात कीजिए।
हल:
A द्वारा अमृतसर पहुँचने में लिया गया समय = दोपहर 12.00 बजे - सुबह 6.00 बजे = 6 घंटे।
कार की एकसमान गति = x किमी/घंटा
∴ A द्वारा तय की गई कुल दूरी = समय x गति = 6x किमी।
∴ दिल्ली और अमृतसर के बीच की दूरी = (6x + 50) किमी।
प्रश्न 2.
अंशिका के विज्ञान में प्राप्त अंक संस्कृत में उसके दो-तिहाई अंकों से 15 अधिक हैं। यदि वह संस्कृत में x अंक प्राप्त करती है, तो विज्ञान में उसके अंक ज्ञात कीजिए।
हल:
अंशिका के संस्कृत में प्राप्त अंक = x
∴ विज्ञान में उसके अंक = \(\frac { 2 }{ 3 }\)x + 15 ∴ इस प्रकार, अंशिका के विज्ञान में प्राप्त अंक = \(\frac { 2 }{ 3 }\)x + 15
