NCERT कक्षा 6 गणित अध्याय 12 अनुपात और समानुपात
Ex 12.1
प्रश्न 1.
एक कक्षा में 20 लड़कियां और 15 लड़के हैं।
(a) लड़कियों की संख्या का लड़कों की संख्या से अनुपात क्या है?
(b) कक्षा में लड़कियों की संख्या का छात्रों की संख्या से अनुपात क्या है?
हल:
(a) लड़कियों की संख्या = 20
लड़कों की संख्या = 15
छात्रों की कुल संख्या = 20 + 15 = 35
∴ लड़कियों की संख्या का लड़कों की संख्या से अनुपात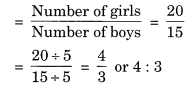
इस प्रकार, आवश्यक अनुपात 4: 3 है।
(b) लड़कियों की संख्या का छात्रों की संख्या से अनुपात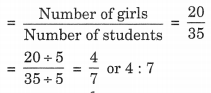
इस प्रकार, आवश्यक अनुपात 4: 7 है।
प्रश्न 2.
एक कक्षा के 30 छात्रों में से 6 को फुटबॉल, 12 को क्रिकेट और शेष को टेनिस पसंद है। अनुपात ज्ञात कीजिए:
(a) फुटबॉल पसंद करने वाले छात्रों की संख्या का टेनिस पसंद करने वाले छात्रों की संख्या से। (b) क्रिकेट पसंद करने वाले छात्रों की संख्या का कुल छात्रों की संख्या से। हल: कक्षा में छात्रों की संख्या = 30 फुटबॉल पसंद करने वाले छात्रों की संख्या = 6 क्रिकेट पसंद करने वाले छात्रों की संख्या = 12 टेनिस पसंद करने वाले छात्रों की संख्या = 30 – (6 + 12) = 30 – 18 = 12
(a) फुटबॉल पसंद करने वाले छात्रों की संख्या का टेनिस पसंद करने वाले छात्रों की संख्या से अनुपात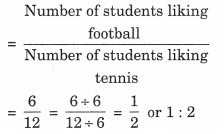
इस प्रकार, आवश्यक अनुपात 1: 2 है।
(b) क्रिकेट पसंद करने वाले छात्रों की संख्या का कुल छात्रों की संख्या से अनुपात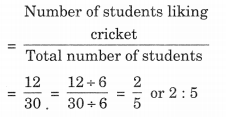
इस प्रकार, आवश्यक अनुपात 2: 5 है।
प्रश्न 3.
आकृति को देखिए और अनुपात ज्ञात कीजिए:
(a) आयत के अंदर त्रिभुजों की संख्या का वृत्तों की संख्या से।
(b) आयत के अंदर वर्गों की संख्या का सभी आकृतियों से।
(c) आयत के अंदर वृत्तों की संख्या का सभी आकृतियों से।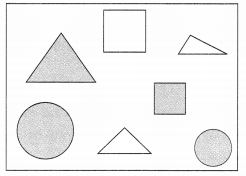
हल:
(a) त्रिभुजों की संख्या 3
वृत्तों की संख्या = 2
∴ त्रिभुजों की संख्या का वृत्तों की संख्या से अनुपात![]()
इस प्रकार, अभीष्ट अनुपात 3 : 2 है।
(b) वर्गों की संख्या = 2
सभी आकृतियों की संख्या = 7
∴ वर्गों की संख्या का सभी आकृतियों की संख्या से अनुपात![]()
इस प्रकार, आवश्यक अनुपात 2: 7 है।
(c) वृत्तों की संख्या का सभी आकृतियों की संख्या से अनुपात![]()
अतः, अभीष्ट अनुपात 2 : 7 है।
प्रश्न 4.
हामिद और अख्तर द्वारा एक घंटे में तय की गई दूरियाँ 9 किमी और 12 किमी हैं। हामिद की गति का अख्तर की गति से अनुपात ज्ञात कीजिए।
हल:
हामिद द्वारा तय की गई दूरी = 9 किमी.
अख्तर द्वारा तय की गई दूरी = 12 किमी.
हामिद की गति = 9 किमी
प्रति घंटा अख्तर की गति = 12 किमी प्रति घंटा
∴ हामिद की गति का अख्तर की गति से अनुपात = अख्तर की गति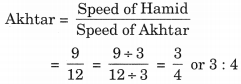
इस प्रकार, अभीष्ट अनुपात 3:4 है।
प्रश्न 5.
निम्नलिखित रिक्त स्थानों की पूर्ति कीजिए: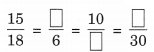
[क्या ये तुल्य अनुपात हैं?]
हल: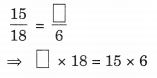

अब भिन्न, हमारे पास हैं
प्रश्न 6.
निम्नलिखित का अनुपात ज्ञात कीजिए:
(a) 81 से 108
(b) 98 से 63
(c) 33 किमी से 121 किमी
(d) 30 मिनट से 45 मिनट
हल:
प्रश्न 7.
निम्नलिखित का अनुपात ज्ञात कीजिए:
(a) 30 मिनट का 1.5 घंटे से
(b) 40 सेमी का 1.5 मीटर से
(c) 55 पैसे का ₹ 1 से
(d) 500 मिलीलीटर का 2 लीटर से
हल:
(a) 1 घंटा = 60 मिनट
∴ 1.5 घंटे = 60 x 1.5 मिनट = 90 मिनट
∴ 30 मिनट का 1.5 घंटे से अनुपात = 30 मिनट का 90 मिनट से अनुपात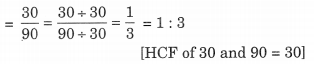
(b) 1 मीटर = 100 सेमी
∴ 1.5 मीटर = 1.5 x 100 सेमी = 150 सेमी.
∴ 40 सेमी का 1.5 मीटर से अनुपात = 40 सेमी का 150 सेमी से अनुपात.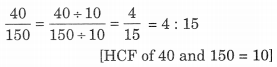
(c) ₹1 = 100 पैसे
∴ 55 पैसे का ₹1 से अनुपात = 55 पैसे का 100 पैसे से अनुपात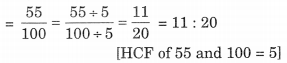
(d) 500 एमएल से 2 लीटर
1 लीटर = 1000 एमएल
∴ 2 लीटर = 2 x 1000 एमएल = 2000 एमएल
∴ 500 एमएल से 2 लीटर का अनुपात = 500 एमएल से 2000 एमएल का अनुपात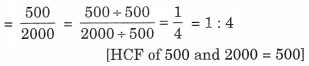
प्रश्न 8.
एक वर्ष में, सीमा ₹ 1,50,000 अर्जित करती है और ₹ 50,000 बचाती है। अनुपात ज्ञात कीजिए:
(a) सीमा द्वारा अर्जित धन और उसके द्वारा बचाई गई राशि।
(b) उसके द्वारा बचाई गई राशि और उसके द्वारा खर्च की गई राशि।
हल:
(a) सीमा द्वारा अर्जित धन = ₹ 1,50,000
उसके द्वारा बचाया गया धन = ₹ 50,000
∴ उसके द्वारा खर्च किया गया धन = ₹ 1,50,000 - ₹ 50,000 = ₹ 1,00,000
∴ सीमा द्वारा अर्जित धन और उसके द्वारा बचाई गई राशि का अनुपात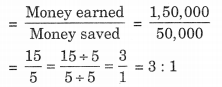
(b) सीमा द्वारा बचाई गई धनराशि का उसके द्वारा बचाई गई धनराशि से अनुपात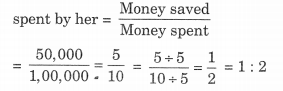
प्रश्न 9.
3300 छात्रों के एक स्कूल में 102 शिक्षक हैं। शिक्षकों की संख्या का छात्रों की संख्या से अनुपात ज्ञात कीजिए।
हल:
शिक्षकों की संख्या = 102
छात्रों की संख्या = 3300
∴ शिक्षकों की संख्या का छात्रों की संख्या से अनुपात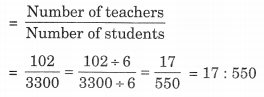
प्रश्न 10.
एक कॉलेज में, 4320 छात्रों में से 2300 लड़कियां हैं, अनुपात ज्ञात कीजिए:
(a) लड़कियों की संख्या का कुल छात्रों की संख्या से।
(b) लड़कों की संख्या का लड़कियों की संख्या से।
(c) लड़कों की संख्या का कुल छात्रों की संख्या से।
हल:
छात्रों की कुल संख्या = 4320
लड़कियों की संख्या = 2300
∴ लड़कों की संख्या = 4320 – 2300 = 2020
(a) लड़कियों की संख्या का कुल छात्रों की संख्या से अनुपात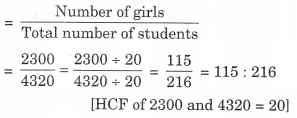
(b) लड़कों की संख्या का लड़कियों की संख्या से अनुपात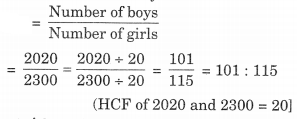
(c) लड़कों की संख्या का कुल छात्रों की संख्या से अनुपात
प्रश्न 11.
एक स्कूल के 1800 छात्रों में से 750 ने बास्केटबॉल, 800 ने क्रिकेट और शेष ने टेबल टेनिस चुना। यदि कोई छात्र केवल एक खेल चुन सकता है, तो अनुपात ज्ञात कीजिए:
(a) बास्केटबॉल चुनने वाले छात्रों की संख्या का टेबल टेनिस चुनने वाले छात्रों की संख्या से।
(b) क्रिकेट चुनने वाले छात्रों की संख्या का बास्केटबॉल चुनने वाले छात्रों की संख्या से।
(c) बास्केटबॉल चुनने वाले छात्रों की संख्या का कुल छात्रों की संख्या से।
हल:
छात्रों की कुल संख्या = 1800
बास्केटबॉल चुनने वाले छात्रों की संख्या = 750
क्रिकेट चुनने वाले छात्रों की संख्या = 800
टेबल टेनिस चुनने वाले शेष छात्रों की संख्या = 1800 - (750 + 800)
= 1800 - 1550 = 250
(a) बास्केटबॉल चुनने वाले छात्रों की संख्या का टेबल टेनिस चुनने वाले छात्रों की संख्या से अनुपात
बास्केटबॉल चुनने वाले छात्रों की संख्या टेबल टेनिस चुनने वाले छात्रों की संख्या
(b) क्रिकेट चुनने वाले छात्रों की संख्या का बास्केटबॉल चुनने वाले छात्रों की संख्या से अनुपात
(c) बास्केटबॉल चुनने वाले छात्रों की संख्या का कुल छात्रों की संख्या से अनुपात
प्रश्न 12.
एक दर्जन पेन की कीमत ₹180 है और 8 बॉल पेन की कीमत ₹56 है। एक पेन की कीमत का बॉल पेन की कीमत से अनुपात ज्ञात कीजिए।
हल:
1 दर्जन, अर्थात् 12 पेन की कीमत = ₹180
∴ 1 पेन की कीमत = ₹\(\frac { 180 }{ 12 }\) = ₹15 8 बॉल पेन की कीमत = ₹56 ∴ 1 बॉल पेन की कीमत = ₹ \(\frac { 56 }{ 8 }\) = ₹7 1 पेन की कीमत का 1 बॉल पेन की कीमत से अनुपात इस प्रकार आवश्यक अनुपात 15 : 7 है।![]()
प्रश्न 13.
कथन पर विचार कीजिए: एक हॉल की चौड़ाई और लंबाई का अनुपात 2:5 है। निम्नलिखित तालिका को पूरा कीजिए जो हॉल की कुछ संभावित चौड़ाई और लंबाई दर्शाती है।
हल:
प्रश्न 14.
शीला और संगीता के बीच 20 पेन को 3:2 के अनुपात में विभाजित करें।
हल:
हमारे पास है 3 + 2 = 5
कुल पेन की संख्या = 20
∴ शीला का हिस्सा = \(\frac { 3 }{ 5 }\) x 20 = 3 x 4 = 12 पेन 5 संगीता का हिस्सा = \(\frac { 2 }{ 5 }\) x 20 = 2 x 4 = 8 पेन। इस प्रकार शीला को 12 पेन और संगीता को 8 पेन मिले।
प्रश्न 15.
एक माँ अपनी बेटियों श्रेया और भूमिका के बीच उनकी आयु के अनुपात में ₹36 बाँटना चाहती है। यदि श्रेया की आयु 15 वर्ष और भूमिका की आयु 12 वर्ष है, तो ज्ञात कीजिए कि श्रेया और भूमिका को कितना मिलेगा?
हल:
दिया गया है:
श्रेया को प्राप्त धनराशि : भूमिका को प्राप्त धनराशि = 15 : 12
∴ योग = 15 + 12 = 27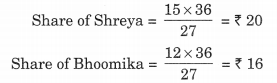
प्रश्न 16.
पिता की वर्तमान आयु 42 वर्ष है और उनके पुत्र की आयु 14 वर्ष है। अनुपात ज्ञात कीजिए:
(a) पिता की वर्तमान आयु का पुत्र की वर्तमान आयु से।
(b) पिता की आयु का पुत्र की आयु से, जब पुत्र 12 वर्ष का था।
(c) 10 वर्ष बाद पिता की आयु का पुत्र की आयु से।
(d) पिता की आयु का पुत्र की आयु से, जब पिता 30 वर्ष का था।
हल:
पिता की वर्तमान आयु = 42 वर्ष।
उनके पुत्र की वर्तमान आयु = 14 वर्ष।
(a) पिता की वर्तमान आयु का पुत्र की वर्तमान आयु से अनुपात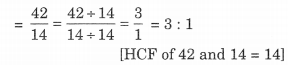
(b) जब पुत्र 12 वर्ष का था, अर्थात् 14 – 12 = 2 वर्ष पहले पिता की आयु = 42 – 2 = 40 वर्ष थी।
पिता की आयु का पुत्र की आयु से अनुपात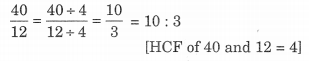
(c) 10 वर्ष बाद पिता की आयु, अर्थात् 42 + 10 = 52 वर्ष, का
10 वर्ष बाद पुत्र की आयु, अर्थात् 14 + 10 = 24 वर्ष से अनुपात![]()
(d) पुत्र की आयु का पिता की आयु से अनुपात जब वह केवल 30 वर्ष का था।
जब पिता 30 वर्ष के थे,
अर्थात् पहले 42 – 30 = 12 वर्ष
पुत्र की आयु = 14 – 12 = 2 वर्ष थी।
∴ अभीष्ट अनुपात![]()
Ex 12.2
प्रश्न 1.
निर्धारित करें कि क्या निम्नलिखित समानुपात में हैं,
(a) 15, 45, 40, 120
(b) 33, 121, 9, 96
(c) 24, 28, 36, 48
(d) 32, 48, 70, 210
(e) 4, 6, 8, 12
(f) 33, 44, 75, 100
हल: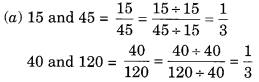
∴ 15 : 45 :: 40 : 120
∴ 15, 45, 40 और 120 समानुपात में हैं।
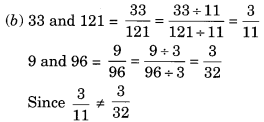
∴ 33, 121, 9 और 96 समानुपात में हैं।
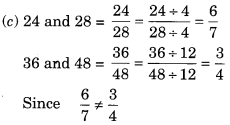
∴ 24, 28, 36 और 48 समानुपात में नहीं हैं।
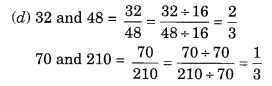
चूँकि \(\frac { 2 }{ 3 }\) ≠ \(\frac { 1 }{ 3 }\) ∴ 32, 48, 70 और 210 समानुपात में नहीं हैं। 4
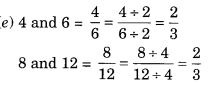
∴ 4 : 6 :: 8 : 12
∴ 4, 6, 8 और 12 समानुपात में हैं।
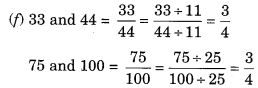
∴ 33 : 44 : : 75 : 100
∴ 33, 44, 75 और 100 समानुपात में हैं।
प्रश्न 2.
निम्नलिखित प्रत्येक कथन के सामने सत्य (T) या असत्य (F) लिखें:
(a) 16 : 24 :: 20 : 30
(b) 21 : 6 :: 35 : 10
(c) 12 : 18 :: 28 : 12
(d) 8 : 9 :: 24 : 27
(e) 5.2 : 3.9 :: 3 : 4
(f) 0.9 : 0.36 :: 10 : 4
हल:
(a) 16 : 24 :: 20 : 30
चरम पदों का गुणनफल = 16 x 30 = 480
मध्य पदों का गुणनफल = 24 x 20 = 480
∴ दिया गया कथन (a) → (T)
(b) 21 : 6 :: 35 : 10
चरम पदों का गुणनफल = 21 x 10 = 210
मध्य पदों का गुणनफल = 6 x 35 = 210
∴ दिया गया कथन (b) → (T)
(c) 12 : 18 :: 28 : 12
चरम पदों का गुणनफल = 12 x 12 = 144
मध्य पदों का गुणनफल = 18 x 28 = 504
क्योंकि 144 ≠ 504
∴ दिया गया कथन (c) → (F)
(d) 8 : 9 :: 24 : 27
चरम पदों का गुणनफल = 8 x 27 = 216
मध्य पदों का गुणनफल = 9 x 24 = 216
दिया गया कथन (d) → (T)
(e) 5.2 : 3.9 :: 3 : 4
चरम पदों का गुणनफल = 5.2 x 4 = 20.8
मध्य पदों का गुणनफल = 3.9 x 3 = 11.7
चूँकि 20.8 ≠ 11.7
दिया गया कथन (e) → (F)
(f) 0.9 : 0.36 :: 10 : 4
चरम पदों का गुणनफल = 0.9 x 4 = 3.6
मध्य पदों का गुणनफल = 0.36 x 10 = 3.6
∴ दिया गया कथन (f) → (T)
प्रश्न 3.
क्या निम्नलिखित कथन सत्य हैं?
(a) 40 व्यक्ति : 200 व्यक्ति = ₹15 : ₹75
(b) 7.5 लीटर : 15 लीटर = 5 किग्रा : 10 किग्रा
(c) 99 किग्रा : 45 किग्रा = ₹44 : ₹20
(d) 32 मी : 64 मी = 6 सेकंड : 12 सेकंड
(e) 45 किमी : 60 किमी = 12 घंटे : 15 घंटे
हल:
(a) 40 व्यक्ति : 200 व्यक्ति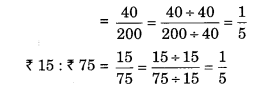
∴ कथन (a) सत्य है।
(b) 7.5 लीटर : 15 लीटर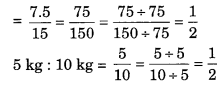
∴ कथन (b) सत्य है।
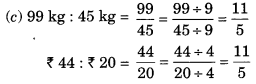
∴ कथन (c) सत्य है।
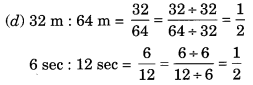
∴ कथन (d) सत्य है।

∴ कथन (e) सत्य नहीं है।
प्रश्न 4.
निर्धारित करें कि क्या निम्नलिखित अनुपात समानुपात बनाते हैं। साथ ही, मध्य पद और चरम पद भी लिखें जहाँ अनुपात समानुपात बनाते हैं।
(a) 25 सेमी : 1 मीटर और ₹ 40 : ₹ 160
(b) 39 लीटर : 65 लीटर और 6 बोतलें : 10 बोतलें
(c) 2 किग्रा : 80 किग्रा और 25 ग्राम : 625 ग्राम
(d) 200 मिलीलीटर : 2.5 लीटर और ₹ 4 : ₹ 50
हल:
(a) 25 सेमी : 1 मीटर = 25 सेमी : 100 सेमी [∵ 1 मीटर = 100 सेमी]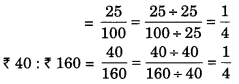
∴ दिए गए अनुपात समानुपात में हैं।
चरम पद 25 सेमी और ₹ 160 हैं।
मध्य पद 1 मीटर और ₹ 40 हैं।
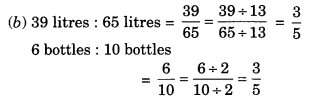
∴ दिए गए अनुपात समानुपात में हैं।
चरम पद 39 लीटर और 10 बोतलें हैं।
मध्य पद 65 लीटर और 6 बोतलें हैं।
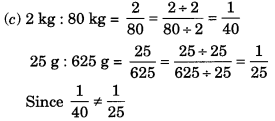
∴ दिए गए अनुपात समानुपात में नहीं हैं।
(d) 200 मिलीलीटर : 2.5 लीटर = 2.5 लीटर = 2.5 x 1000 मिलीलीटर = 2500 मिलीलीटर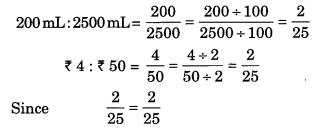
∴ दिए गए अनुपात समानुपात में हैं।
चरम पद 200 मिलीलीटर और ₹ 50 हैं।
मध्य पद 2.5 लीटर और ₹ 4 हैं।
Ex 12.3
प्रश्न 1.
यदि 7 मीटर कपड़े का मूल्य ₹294 है, तो 5 मीटर कपड़े का मूल्य ज्ञात कीजिए।
हल:
एकक विधि का उपयोग करते हुए, 7 मीटर कपड़े का मूल्य = ₹294
1 मीटर कपड़े का मूल्य = ₹ \(\frac { 294 }{ 7 }\) 5 मीटर कपड़े का मूल्य = ₹(\(\frac { 294 }{ 7 }\) x 5) = ₹(42 x 5) = ₹210 इस प्रकार, अभीष्ट मूल्य = ₹210
प्रश्न 2.
एकता 10 दिनों में ₹ 1500 कमाती है। वह 30 दिनों में कितना कमाएगी?
हल:
10 दिनों में एकता ₹ 1500 कमाती है।
1 दिन में एकता ₹ \(\frac { 1500 }{ 10 }\) कमाएगी। 30 दिनों में एकता ₹\(\frac { 1500 }{ 10 }\) x 30 = ₹4500 कमाएगी। इस प्रकार 30 दिनों में एकता द्वारा अर्जित धन = ₹4500।
प्रश्न 3.
यदि पिछले 3 दिनों में 276 मिमी बारिश हुई है, तो एक पूरे सप्ताह (7 दिन) में कितने सेंटीमीटर बारिश होगी? मान लीजिए कि बारिश उसी दर से जारी है।
हल:
पिछले 3 दिनों में बारिश = 276 मिमी।
1 दिन में बारिश = \(\frac { 276 }{ 3 }\) मिमी। 7 दिनों में बारिश होगी = \(\frac { 276 }{ 3 }\) x 7 मिमी। = 92 x 7 मिमी = 644 मिमी या 64.4 सेमी [∵ 1 सेमी = 10 मिमी] इस प्रकार, सप्ताह में बारिश की मात्रा = 64.4 सेमी।
प्रश्न 4.
5 किग्रा गेहूं का मूल्य ₹ 30.50 है।
(a) 8 किग्रा गेहूं का मूल्य क्या होगा?
(b) ₹ 61 में कितना गेहूं खरीदा जा सकता है?
हल:
(a) 5 किग्रा गेहूं का मूल्य = ₹ 30.50
1 किग्रा गेहूं का मूल्य = ₹ \(\frac { 30.50 }{ 5 }\) 8 किग्रा गेहूं का मूल्य = ₹( \(\frac { 30.50 }{ 5 }\) x 8) = ₹ 48.80 इस प्रकार, अभीष्ट मूल्य = ₹ 48.80
(b) ₹ 30.50 में खरीदे गए गेहूं की मात्रा = 5 किग्रा
₹ 1 में खरीदे गए गेहूं की मात्रा = \(\frac { 5 }{ 30.50 }\) किग्रा ₹ 61 में खरीदे गए गेहूं की मात्रा = \(\frac { 5 x 61 }{ 30.50 }\) किग्रा इस प्रकार, गेहूं की आवश्यक मात्रा = 10 किग्रा
प्रश्न 5.
पिछले 30 दिनों में तापमान 15 डिग्री सेल्सियस गिरा है। यदि तापमान में गिरावट की दर समान रहती है, तो अगले 10 दिनों में तापमान कितने डिग्री गिरेगा?
हल:
पिछले 3.0 दिनों में तापमान में गिरावट की मात्रा = 15 डिग्री सेल्सियस
पिछले 1 दिन में तापमान में गिरावट की मात्रा = \(\frac { 15 }{ 30 }\) डिग्री सेल्सियस पिछले 10 दिनों में तापमान में गिरावट की मात्रा = \(\frac { 15 }{ 30 }\) x 10 डिग्री सेल्सियस = 5 डिग्री सेल्सियस इस प्रकार पिछले 10 दिनों में तापमान में आवश्यक गिरावट = 5 डिग्री सेल्सियस
प्रश्न 6.
शाइना 3 महीने के लिए ₹ 7500 किराए के रूप में देती है। यदि प्रति माह किराया समान रहता है, तो उसे पूरे वर्ष के लिए कितना भुगतान करना होगा?
हल:
3 महीने में भुगतान किया गया किराया = ₹ 7500
1 महीने में भुगतान किया गया किराया = ₹ \(\frac { 7500 }{ 3 }\) 12 महीनों में भुगतान किया गया किराया = ₹ ( \(\frac { 7500 }{ 3 }\) x 12) = ₹ 30,000 इस प्रकार 1 वर्ष में भुगतान किया गया किराया = ₹ 30,000
प्रश्न 7.
4 दर्जन केलों का मूल्य ₹ 60 है। ₹ 12.50 में कितने केले खरीदे जा सकते हैं?
हल:
∵ 1 दर्जन = 12 इकाई
∴ 4 दर्जन केले = 12 x 4 = 48 केले
₹ 60 है 4 दर्जन का मूल्य = 4 x 12 = 48 केले
₹ 1 का मूल्य = \(\frac { 48 }{ 60 }\) केले 60. ₹ 12.50 का मूल्य = \(\frac { 600 }{ 60 }\) केले = 10 केले इस प्रकार केलों की आवश्यक संख्या = 10
प्रश्न 8.
72 पुस्तकों का वजन 9 किग्रा है। ऐसी 40 पुस्तकों का वजन क्या है?
हल:
72 पुस्तकों का वजन = 9 किग्रा
1 पुस्तक का वजन = \(\frac { 9 }{ 72 }\) किग्रा 40 पुस्तकों का वजन = \(\frac { 9 }{ 72 }\) x 40 किग्रा = 5 किग्रा अतः, आवश्यक वजन = 5 किग्रा।
प्रश्न 9.
एक ट्रक को 594 किमी की दूरी तय करने के लिए 108 लीटर डीजल की आवश्यकता होती है। 1650 किमी की दूरी तय करने के लिए ट्रक को कितने डीजल की आवश्यकता होगी?
हल:
594 किमी तय करने के लिए आवश्यक डीजल की मात्रा = 108 लीटर।
1 किमी तय करने के लिए डीजल की मात्रा होगी, आवश्यक = \(\frac { 108 }{ 594 }\) लीटर 1650 किमी तय करने के लिए आवश्यक डीजल की मात्रा = \(\frac { 108 × 1650 }{ 594 }\) लीटर = 300 लीटर इस प्रकार, डीजल की आवश्यक मात्रा = 300 लीटर
प्रश्न 10.
राजू ₹150 में 10 पेन खरीदता है और मनीष ₹84 में 7 पेन खरीदता है। क्या आप बता सकते हैं कि पेन किसे सस्ते मिले?
हल:
राजू के लिए,
10 पेन की कीमत = ₹150
1 पेन की कीमत = ₹ \(\frac { 150 }{ 10 }\) = ₹15 मनीष के लिए, 7 पेन की कीमत = ₹84 1 पेन की कीमत = ₹ \(\frac { 84 }{ 7 }\) = ₹12 ∴ ₹12 < ₹15 इस प्रकार, मनीष को राजू से सस्ते पेन मिले।
प्रश्न 11.
अनीश ने 6 ओवर में 42 रन बनाए और अनूप ने 7 ओवर में 63 रन बनाए। किसने प्रति ओवर अधिक रन बनाए?
हल:
अनीश द्वारा 6 ओवर में बनाए गए रनों की संख्या = 42
उसके द्वारा 1 ओवर में बनाए गए रनों की संख्या = \(\frac { 42 }{ 6 }\) = 7 रन। अनूप द्वारा 7 ओवर में बनाए गए रनों की संख्या = 63 उसके द्वारा 1 ओवर में बनाए गए रनों की संख्या = \(\frac { 63 }{ 7 }\) = 9 रन। ∴ 9 रन > 7 रन। इस प्रकार, अनूप ने अधिक रन बनाए हैं।
InText Questions
लघु उत्तरीय प्रश्न
प्रश्न 1.
हरा रंग नीले, पीले और सफेद रंग को 2 : 7 : 1 के अनुपात में मिलाकर बनाया जाता है। 64 लीटर हरा रंग बनाने के लिए कितने नीले रंग की आवश्यकता होगी?
हल:
यहाँ, अनुपातों का योग = 2 + 7 + 1 = 10
∴ हरे रंग की कुल मात्रा = 64 लीटर
नीले रंग की मात्रा = \(\frac { 2 }{ 10 }\) x 64 = 12.8 लीटर इसलिए, आवश्यक नीला रंग = 12.8 लीटर।210 x 64 = 12.8 litres
प्रश्न 2.
आकृति से अनुपात ज्ञात कीजिए:
(a) वर्गों की संख्या का त्रिभुजों की संख्या से।
(b) वृत्तों की संख्या का आयतों की संख्या से।
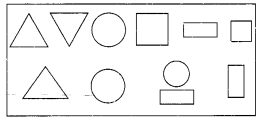
हल:
(a) वर्गों की संख्या = 2
त्रिभुजों की संख्या = 3 2
∴ अनुपात = \(\frac { 2 }{ 3 }\) या 2 : 323 or 2 : 3
(b) वृत्तों की संख्या = 3
आयतों की संख्या = 3
∴ अनुपात = \(\frac { 3 }{ 3 }\) या 1 : 133 or 1 : 1
प्रश्न 3.
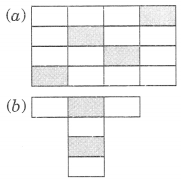
निम्नलिखित प्रत्येक आकृति में, छायांकित भाग का अछायांकित भाग से अनुपात ज्ञात कीजिए।
हल:
(a) छायांकित भागों की संख्या = 4
अछायांकित भागों की संख्या = 12
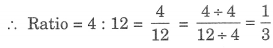
आवश्यक अनुपात = 1 : 3
(b) छायांकित भागों की संख्या = 2
अछायांकित भागों की संख्या = 4
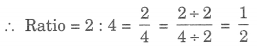
आवश्यक अनुपात = 1 : 2
प्रश्न 4.
क्या 20, 25, 12, 15 समानुपात में हैं?
हल:
हमारे पास 20, 25, 12, 15 है।
चरम संख्याओं का गुणनफल = 20 x 15 = 300
मध्य संख्याओं का गुणनफल = 25 x 12 = 300
क्योंकि दोनों गुणनफल समान हैं।
∴ चार संख्याएँ 20, 25, 12, 15 समानुपात में हैं।
प्रश्न 5.
एक समानुपात में पहला, दूसरा और चौथा पद क्रमशः 32, 112, 217 हैं। तीसरा पद ज्ञात कीजिए।
हल:
मान लीजिए तीसरा पद x है।
∴ 32, 112, x और 217 समानुपात में हैं।
∴ 32 : 112 :: x : 217
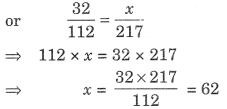
अतः, तीसरा पद = 62 है।
प्रश्न 6.
x का मान ज्ञात कीजिए, यदि
(a) 8, x, x, 50 समानुपात में हैं।
(b) 36, 90, 90, x समानुपात में हैं।
हल:
(a) चूँकि 8, x, x, 50 समानुपात में हैं।
∴ x × x = 8 × 50
⇒ x 2 = 400
∴ x = 20
(b) चूँकि 36, 90, 90, x समानुपात में हैं।
∴ 36 × x = 90 × 90
⇒ x = \(\frac { 90\times 90 }{ 36 }\) = 225 ∴ x = 22590×9036 = 225
प्रश्न 7.
10 मेजों का मूल्य ₹ 7500 है। ₹ 9000 से खरीदी जा सकने वाली मेजों की संख्या ज्ञात कीजिए।
हल:
₹ 7500 में खरीदी गई मेजों की संख्या = 10
₹ 1 में खरीदी गई मेजों की संख्या = \(\frac { 10 }{ 7500 }\) ∴ ₹ 9000 में खरीदी गई मेजों की संख्या = \(\frac { 10\times 9000 }{ 7500 }\) = 12107500
10×90007500 = 12
प्रश्न 8.
12 पेन वाले 39 पैकेटों का मूल्य ₹ 374.40 है। 10 पेन वाले 52 पैकेटों का मूल्य ज्ञात कीजिए।
हल:
1 पैकेट में पेनों की संख्या = 12
39 पैकेटों में पेनों की संख्या = 12 x 39 = 468
1 पैकेट में पेनों की संख्या = 10
52 पैकेटों में पेनों की संख्या = 10 x 52 = 520
अब 468 पेनों का मूल्य = ₹ 374.40

हरा रंग नीले, पीले और सफेद रंग को 2 : 7 : 1 के अनुपात में मिलाकर बनाया जाता है। 64 लीटर हरा रंग बनाने के लिए कितने नीले रंग की आवश्यकता होगी?
हल:
यहाँ, अनुपातों का योग = 2 + 7 + 1 = 10
∴ हरे रंग की कुल मात्रा = 64 लीटर
नीले रंग की मात्रा = \(\frac { 2 }{ 10 }\) x 64 = 12.8 लीटर इसलिए, आवश्यक नीला रंग = 12.8 लीटर।
आकृति से अनुपात ज्ञात कीजिए:
(a) वर्गों की संख्या का त्रिभुजों की संख्या से।
(b) वृत्तों की संख्या का आयतों की संख्या से।

हल:
(a) वर्गों की संख्या = 2
त्रिभुजों की संख्या = 3 2
∴ अनुपात = \(\frac { 2 }{ 3 }\) या 2 : 3
आयतों की संख्या = 3
∴ अनुपात = \(\frac { 3 }{ 3 }\) या 1 : 1
निम्नलिखित प्रत्येक आकृति में, छायांकित भाग का अछायांकित भाग से अनुपात ज्ञात कीजिए।

हल:
(a) छायांकित भागों की संख्या = 4
अछायांकित भागों की संख्या = 12
आवश्यक अनुपात = 1 : 3
अछायांकित भागों की संख्या = 4
आवश्यक अनुपात = 1 : 2
क्या 20, 25, 12, 15 समानुपात में हैं?
हल:
हमारे पास 20, 25, 12, 15 है।
चरम संख्याओं का गुणनफल = 20 x 15 = 300
मध्य संख्याओं का गुणनफल = 25 x 12 = 300
क्योंकि दोनों गुणनफल समान हैं।
∴ चार संख्याएँ 20, 25, 12, 15 समानुपात में हैं।
एक समानुपात में पहला, दूसरा और चौथा पद क्रमशः 32, 112, 217 हैं। तीसरा पद ज्ञात कीजिए।
हल:
मान लीजिए तीसरा पद x है।
∴ 32, 112, x और 217 समानुपात में हैं।
∴ 32 : 112 :: x : 217
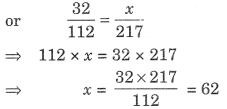
अतः, तीसरा पद = 62 है।
x का मान ज्ञात कीजिए, यदि
(a) 8, x, x, 50 समानुपात में हैं।
(b) 36, 90, 90, x समानुपात में हैं।
हल:
(a) चूँकि 8, x, x, 50 समानुपात में हैं।
∴ x × x = 8 × 50
⇒ x 2 = 400
∴ x = 20
∴ 36 × x = 90 × 90
⇒ x = \(\frac { 90\times 90 }{ 36 }\) = 225 ∴ x = 225
10 मेजों का मूल्य ₹ 7500 है। ₹ 9000 से खरीदी जा सकने वाली मेजों की संख्या ज्ञात कीजिए।
हल:
₹ 7500 में खरीदी गई मेजों की संख्या = 10
₹ 1 में खरीदी गई मेजों की संख्या = \(\frac { 10 }{ 7500 }\) ∴ ₹ 9000 में खरीदी गई मेजों की संख्या = \(\frac { 10\times 9000 }{ 7500 }\) = 12
12 पेन वाले 39 पैकेटों का मूल्य ₹ 374.40 है। 10 पेन वाले 52 पैकेटों का मूल्य ज्ञात कीजिए।
हल:
1 पैकेट में पेनों की संख्या = 12
39 पैकेटों में पेनों की संख्या = 12 x 39 = 468
1 पैकेट में पेनों की संख्या = 10
52 पैकेटों में पेनों की संख्या = 10 x 52 = 520
अब 468 पेनों का मूल्य = ₹ 374.40

अति लघु उत्तरीय प्रश्न
प्रश्न 1.
75 सेमी और 1.5 मीटर का अनुपात ज्ञात कीजिए।
हल:
दी गई संख्याएँ समान इकाइयों में नहीं हैं। इसलिए, उन्हें समान इकाइयों में बदलने पर:
1.5 मीटर = 1.5 x 100 सेमी = 150 सेमी
[∵ 1 मीटर = 100 सेमी]
∴ अभीष्ट अनुपात 75 सेमी : 150 सेमी है।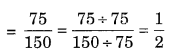
∴ अभीष्ट अनुपात = 1 : 2
प्रश्न 2.
3 : 5 के दो तुल्य अनुपात बताइए।
हल: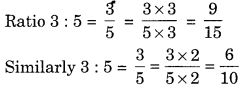
इस प्रकार, 9 : 15 और 6 : 10, 3 : 5 के दो तुल्य अनुपात हैं।
प्रश्न 3.
रिक्त बॉक्स भरें![]()
।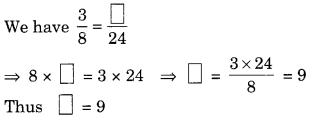
प्रश्न 4.
जाँच कीजिए कि दिए गए अनुपात समतुल्य हैं या नहीं। \(\frac { 2 }{ 7 }\), \(\frac { 6 }{ 21 }\) हल: ∴ ये समतुल्य अनुपात हैं।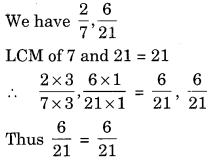
प्रश्न 5.
60 को 2 : 3 के अनुपात में विभाजित करें।
हल:
योग = 2 + 3 = 5
∴ पहला भाग = \(\frac { 2 }{ 5 }\) x 60 =24 5 ∴ दूसरा भाग = \(\frac { 3 }{ 5 }\) x 60 =36 5 इस प्रकार, आवश्यक दो भाग = 24 और 36।
प्रश्न 6.
निम्नलिखित का अनुपात ज्ञात कीजिए:
(a) 56 से 63.
(b) 55 से 120.
हल: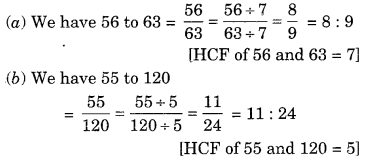
प्रश्न 7.
रमेश ने एक बैंक में ₹ 2050 जमा किए और जनवरी के महीने में उसने महीने की आखिरी तारीख को अपने खाते से ₹ 410 निकाल लिए। अनुपात ज्ञात कीजिए
(a) निकाली गई राशि का कुल जमा राशि से।
(b) निकाली गई राशि का बैंक में शेष राशि से।
हल:
कुल जमा राशि = ₹ 2050
निकाली गई राशि = ₹ 410
बैंक में शेष राशि = ₹ 2050 - ₹ 410 = ₹ 1640
(a) निकाली गई राशि का कुल जमा राशि से अनुपात![]()
∴ आवश्यक अनुपात = 1 : 5
(b) निकाली गई राशि का बैंक में शेष राशि से अनुपात![]()
∴ आवश्यक अनुपात = 1 : 4
प्रश्न 8.
एक कक्षा में 180 विद्यार्थी हैं। लड़कियों की संख्या 75 है। लड़कियों का लड़कों की संख्या से अनुपात ज्ञात कीजिए।
हल:
विद्यार्थियों की कुल संख्या = 180
लड़कियों की संख्या = 75
लड़कों की संख्या = 180 – 75 = 105
∴ लड़कियों की संख्या का लड़कों की संख्या से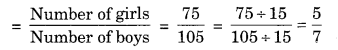
अनुपात = 5 : 7
