NCERT कक्षा 6 गणित अध्याय 10 क्षेत्रमिति
Ex 10.1
प्रश्न 1.
निम्नलिखित आकृतियों में से प्रत्येक का परिमाप ज्ञात कीजिए: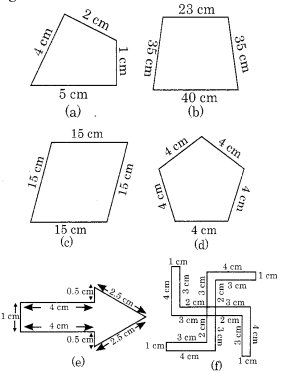
हल:
(a) अभीष्ट परिमाप
= 4 सेमी + 2 सेमी + 1 सेमी + 5 सेमी = 12 सेमी
(b) अभीष्ट परिमाप
= 40 सेमी + 35 सेमी + 23 सेमी + 35 सेमी
= 133 सेमी या 1.33 मीटर
(c) अभीष्ट परिमाप
= 15 सेमी + 15 सेमी + 15 सेमी + 15 सेमी = 15 सेमी x 4 = 60 सेमी
(d) अभीष्ट परिमाप
= 4 सेमी + 4 सेमी + 4 सेमी + 4 सेमी + 4 सेमी - 4 सेमी x 5 = 20 सेमी
(e) अभीष्ट परिमाप
= 4 सेमी + 0.5 सेमी + 2.5 सेमी + 2.5 सेमी + 0.5 सेमी + 4 सेमी + 1 सेमी
= 15 सेमी
(f) अभीष्ट परिमाप = 4 सेमी + 1 सेमी + 3 सेमी + 2 सेमी + 3 सेमी + 4 सेमी + 1 सेमी + 3 सेमी + 2 सेमी + 3 सेमी + 4 सेमी + 1 सेमी + 3 सेमी + 2 सेमी + 3 सेमी + 4 सेमी + 1 सेमी + 3 सेमी + 2 सेमी + 3 सेमी
= 52 सेमी
प्रश्न 2.
40 सेमी x 10 सेमी भुजाओं वाले एक आयताकार डिब्बे के ढक्कन को चारों ओर से टेप से सील किया गया है। आवश्यक टेप की लंबाई कितनी है?
हल:
आवश्यक टेप की कुल लंबाई = आयताकार ढक्कन का परिमाप
= 2 [लंबाई + चौड़ाई] = 2 x [40 + 10]
= 2 x 50 = 100 सेमी
प्रश्न 3.
एक मेज़ की सतह का माप 2 मीटर 25 सेमी x 1 मीटर 50 सेमी है। मेज़ की सतह का परिमाप क्या है?
हल:
मेज़ की सतह की लंबाई = 2 मीटर 25 सेमी
मेज़ की सतह की चौड़ाई = 1 मीटर 50 सेमी
∴ मेज़ की सतह का परिमाप = 2 [लंबाई + चौड़ाई]
= 2 [2 मीटर 25 सेमी + 1 मीटर 50 सेमी]
= 2 x 3 मीटर 75 सेमी
= 7 मीटर 50 सेमी
= 7.5 मीटर
प्रश्न 4.
32 सेमी लंबाई और 21 सेमी चौड़ाई वाले एक फोटोग्राफ को फ्रेम करने के लिए आवश्यक लकड़ी की पट्टी की लंबाई क्या है?
हल:
पट्टी की लंबाई = 32 सेमी
पट्टी की चौड़ाई = 21 सेमी
∴ परिमाप = 2 [लंबाई + चौड़ाई]
= 2 [32 सेमी + 21 सेमी]
= 2 x 53 सेमी = 106 सेमी
अतः, पट्टी की आवश्यक लंबाई = 106 सेमी या 1 मीटर 6 सेमी।
प्रश्न 5.
भूमि के एक आयताकार टुकड़े का माप 0.7 किमी x 0.5 किमी है। प्रत्येक भुजा को तारों की 4 पंक्तियों से घेरा जाना है। आवश्यक तार की लंबाई क्या है?
हल:
भूमि के आयताकार टुकड़े की लंबाई = 0.7 किमी = 0.7 x 1000 मीटर = 700 मीटर
भूमि के आयताकार टुकड़े की चौड़ाई = 0.5 किमी = 0.5 x 1000 मीटर = 500 मीटर
∴ आयताकार भूमि का परिमाप
= 2 [लंबाई + चौड़ाई]
= 2 [700 मीटर + 500 मीटर]
= 2400 मीटर।
भूमि के 4 चक्कर लगाने के लिए आवश्यक तार की लंबाई = 4 x 2400 = 9600 मीटर = 9.6 किमी।
प्रश्न 6.
निम्नलिखित आकृतियों में से प्रत्येक का परिमाप ज्ञात कीजिए:
(a) 3 सेमी, 4 सेमी और 5 सेमी भुजाओं वाला एक त्रिभुज।
(b) 9 सेमी भुजा वाला एक समबाहु त्रिभुज।
(c) 8 सेमी प्रत्येक बराबर भुजाओं और 6 सेमी तीसरी भुजा वाला एक समद्विबाहु त्रिभुज।
हल:
(a) हम जानते हैं कि दिए गए त्रिभुज का परिमाप = त्रिभुज की सभी भुजाओं का योग
∴ त्रिभुज का परिमाप = 3 सेमी + 4 सेमी + 5 सेमी = 12 सेमी (b) हम जानते हैं कि दिए गए त्रिभुज का परिमाप = त्रिभुज की सभी भुजाओं का योग = (9 + 9 + 9) = 27 सेमी (c) दिए गए समद्विबाहु त्रिभुज का परिमाप = त्रिभुज की सभी भुजाओं का योग = (8 + 8 + 6) सेमी = 22 सेमी
प्रश्न 7.
10 सेमी, 14 सेमी और 15 सेमी भुजाओं वाले त्रिभुज का परिमाप ज्ञात कीजिए।
हल:
त्रिभुज का परिमाप = त्रिभुज की सभी भुजाओं का योग
= 10 सेमी + 14 सेमी + 15 सेमी
= 39 सेमी
प्रश्न 8.
एक सम षट्भुज का परिमाप ज्ञात कीजिए जिसकी प्रत्येक भुजा 8 मीटर है।
हल:
एक सम षट्भुज का परिमाप = 6 x भुजा = 6 x 8 मीटर = 48 मीटर।
प्रश्न 9.
उस वर्ग की भुजा ज्ञात कीजिए जिसका परिमाप 20 मीटर है।
हल:
वर्ग का परिमाप = 4 x भुजा
20 = 4 x भुजा
∴ भुजा = 20 मीटर ÷ 4 = 5 मीटर
प्रश्न 10.
एक सम पंचभुज का परिमाप 100 सेमी है। इसकी प्रत्येक भुजा की लंबाई कितनी है?
हल:
हमारे पास है :
सम पंचभुज का परिमाप = 100 सेमी
सम पंचभुज में भुजाओं की संख्या = 5
∴ प्रत्येक भुजा की लंबाई = परिमाप ÷ भुजाओं की संख्या
= 100 सेमी ÷ 5 = 20 सेमी।
प्रश्न 11.
एक डोरी 30 सेमी लंबी है। यदि इस डोरी का उपयोग निम्नलिखित बनाने के लिए किया जाए तो प्रत्येक भुजा की लंबाई क्या होगी:
(a) एक वर्ग?
(b) एक समबाहु त्रिभुज?
(c) एक सम षट्भुज?
हल:
(a) डोरी की लंबाई = 30 सेमी
एक वर्ग में बराबर भुजाओं की संख्या = 4
∴ वर्ग की प्रत्येक भुजा की लंबाई = 30 सेमी ÷ 4 = 7.50 सेमी।
(b) डोरी की लंबाई = 30 सेमी
समबाहु त्रिभुज में समान भुजाओं की संख्या = 3
∴ समबाहु त्रिभुज की प्रत्येक भुजा की लंबाई = 30 सेमी ÷ 3 = 10 सेमी
(c) डोरी की लंबाई = 30 सेमी
सम षट्भुज में बराबर भुजाओं की संख्या = 6
∴ सम षट्भुज की प्रत्येक भुजा की लंबाई = 30 सेमी ÷ 6 = 5 सेमी
प्रश्न 12.
एक त्रिभुज की दो भुजाएँ 12 सेमी और 14 सेमी हैं। त्रिभुज का परिमाप 36 सेमी है। इसकी तीसरी भुजा क्या है?
हल:
त्रिभुज का परिमाप = 36 सेमी।
इसकी दो भुजाओं की लंबाई 12 सेमी और 14 सेमी है।
त्रिभुज की तीसरी भुजा की लंबाई = 36 – (12 + 14) सेमी
= (36 – 26) सेमी = 10 सेमी
प्रश्न 13.
250 मीटर भुजा वाले एक वर्गाकार पार्क में ₹20 प्रति मीटर की दर से बाड़ लगाने की लागत ज्ञात कीजिए।
हल:
वर्ग की भुजा की लंबाई = 250 मीटर
∴ वर्ग का परिमाप = 250 मीटर x 4 = 1000 मीटर
बाड़ लगाने की दर = ₹20 प्रति मीटर
∴ बाड़ लगाने की लागत = ₹20 x 1000 = ₹20,000
प्रश्न 14.
175 मीटर लंबाई और 125 मीटर चौड़ाई वाले एक आयताकार पार्क में ₹12 प्रति मीटर की दर से बाड़ लगाने की लागत ज्ञात कीजिए।
हल:
आयताकार पार्क की लंबाई = 175 मीटर
आयताकार पार्क की चौड़ाई = 125 मीटर
∴ पार्क का परिमाप = 2 [लंबाई + चौड़ाई]
= 2[175 मीटर + 125 मीटर]
= 2 x 300 मीटर = 600 मीटर
बाड़ लगाने की दर = ₹12 प्रति मीटर बाड़ लगाने की लागत = ₹12 x 600 = ₹7200
प्रश्न 15.
स्वीटी 75 मीटर भुजा वाले एक वर्गाकार पार्क के चारों ओर दौड़ती है। बुलबुल 60 मीटर लंबाई और 45 मीटर चौड़ाई वाले एक आयताकार पार्क के चारों ओर दौड़ती है। कौन कम दूरी तय करता है?
हल:
वर्गाकार पार्क की भुजा = 75 मीटर
∴ इसका परिमाप = 4 x 75 मीटर = 300 मीटर
आयताकार पार्क का परिमाप = 2 [लंबाई + चौड़ाई]
= 2 [60 मीटर + 45 मीटर]
= 2 x 105 मीटर = 210 मीटर।
चूँकि 210 मीटर < 300 मीटर।
इसलिए, बुलबुल कम दूरी तय करती है।
प्रश्न 16.
निम्नलिखित आकृतियों में से प्रत्येक का परिमाप क्या है? उत्तरों से आप क्या निष्कर्ष निकालते हैं?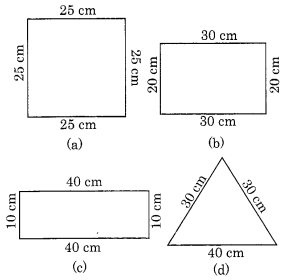
हल:
(a) वर्ग का परिमाप = 25 सेमी + 25 सेमी + 25 सेमी + 25 सेमी = 4 x 25 सेमी = 100 सेमी
(b) आयत का परिमाप = 30 सेमी + 20 सेमी + 30 सेमी + 20 सेमी - 2 [30 सेमी + 20 सेमी] = 2 x 50 सेमी = 100 सेमी
(c) आयत का परिमाप = 40 सेमी + 10 सेमी + 40 सेमी + 10 सेमी = 2 [40 सेमी + 10 सेमी] = 2 x 50 सेमी = 100 सेमी
(d) त्रिभुज का परिमाप = सभी भुजाओं का योग = 30 सेमी + 30 सेमी + 40 सेमी = 100 सेमी उपरोक्त उत्तरों से, हम यह निष्कर्ष निकालते हैं कि विभिन्न आकृतियों के परिमाप समान हो सकते हैं।
प्रश्न 17.
अवनीत 9 वर्गाकार फ़र्श स्लैब खरीदता है, जिनमें से प्रत्येक की भुजा
(a) उसकी व्यवस्था का परिमाप क्या है [चित्र (i)]?
(b) शैरी को उसकी व्यवस्था पसंद नहीं है। वह उसे उन्हें क्रॉस की तरह बिछाने के लिए कहती है। उसकी व्यवस्था का परिमाप क्या है [चित्र (ii)]?
(c) किसका परिमाप अधिक है?
(d) अवनीत सोचता है कि क्या इससे भी बड़ा परिमाप प्राप्त करने का कोई तरीका है। क्या आप ऐसा करने का कोई तरीका खोज सकते हैं? (फ़र्श स्लैब को पूरे किनारों पर मिलना चाहिए, अर्थात, उन्हें तोड़ा नहीं जा सकता)।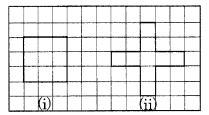
हल:
(a) व्यवस्था भुजा वाले एक वर्ग के रूप में है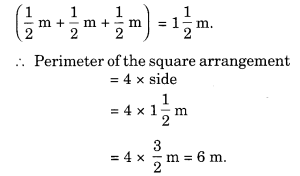
(b) क्रॉस-व्यवस्था का परिमाप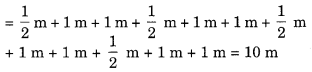
(c) चूँकि 10 m > 6 m
∴ क्रॉस-व्यवस्था का परिमाप अधिक है।
(d) टाइल्स की कुल संख्या = 9
∴ हमारे पास निम्नलिखित व्यवस्था है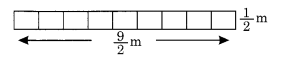
उपरोक्त व्यवस्था में भी अधिक परिमाप होगा।
Ex 10.2
प्रश्न 1.
निम्नलिखित आकृतियों का क्षेत्रफल वर्ग गिनकर ज्ञात कीजिए: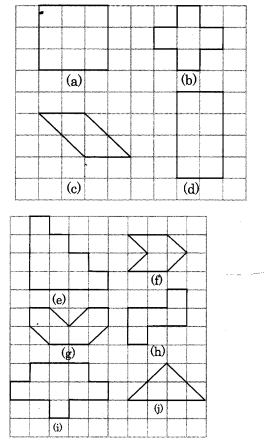
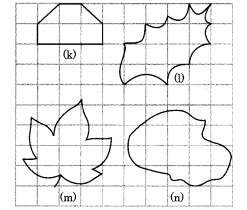
हल:
(a) पूर्ण वर्गों की संख्या = 9
1 वर्ग का क्षेत्रफल = 1 वर्ग इकाई
∴ 9 वर्गों का क्षेत्रफल = 9 x 1 वर्ग इकाई
= 9 वर्ग इकाई।
अतः, 9 वर्गों द्वारा आवृत भाग का क्षेत्रफल = 9 वर्ग इकाई
(b) पूर्ण वर्गों की संख्या = 5
∴ आकृति का क्षेत्रफल = 5 x 1 वर्ग इकाई = 5 वर्ग इकाई
(c) पूर्ण वर्गों की संख्या = 2
आधे वर्गों की संख्या = 4
∴ ढकी हुई आकृति का क्षेत्रफल = 2 x 1 + 4 x
= 4 वर्ग इकाई
(d) पूर्ण वर्गों की संख्या = 8
∴ आकृति के ढके हुए भाग का क्षेत्रफल = 8 x 1 वर्ग इकाई
= 8 वर्ग इकाई
(e) पूर्ण वर्गों की संख्या = 10
आकृति द्वारा घेरा गया क्षेत्रफल = 10 x 1 वर्ग इकाई = 10 वर्ग इकाई.
(f) पूर्ण वर्गों की संख्या = 2
आधे वर्गों की संख्या = 4
∴ ढकी हुई आकृति का क्षेत्रफल = (2 x 1 + 4 x
= (2 + 2) वर्ग इकाई = 4 वर्ग इकाई.
(g) पूर्ण वर्गों की संख्या = 4
आधे वर्गों की संख्या = 4
∴ ढकी हुई आकृति का क्षेत्रफल = (4 x 1 + 4 x
= (4 + 2) वर्ग इकाई = 6 वर्ग इकाई.
(h) पूर्ण वर्गों की संख्या = 5
∴ ढकी हुई आकृति का क्षेत्रफल = 5 x 1 वर्ग इकाई = 5 वर्ग इकाई।
(i) पूर्ण वर्गों की संख्या = 9
∴ ढकी हुई आकृति का क्षेत्रफल = 9 x 1 वर्ग इकाई
= 9 वर्ग इकाई।
(j) पूर्ण वर्गों की संख्या = 2
अर्ध वर्गों की संख्या = 4
∴ ढकी हुई आकृति का क्षेत्रफल = (2 x 1 + 4 x
= (2 + 2) वर्ग इकाई = 4 वर्ग इकाई।
(k) पूर्ण वर्गों की संख्या = 4
अर्ध वर्गों की संख्या = 2
∴ ढकी हुई आकृति का क्षेत्रफल = (4 x 1 + 2 x
= (4 + 4) वर्ग इकाई
= 5 वर्ग इकाई
(l) पूर्ण वर्गों की संख्या = 4
आधे से अधिक वर्गों की संख्या = 3
आधे वर्गों की संख्या = 2
∴ ढकी हुई आकृति का क्षेत्रफल = (4 x 1 + 3 x 1 + 2 x
= (4 + 3 + 1) वर्ग इकाई = 8 वर्ग इकाई.
(m) पूर्ण वर्गों की संख्या = 6
आधे से अधिक वर्गों की संख्या = 8
ढकी हुई आकृति का क्षेत्रफल = (6 x 1 + 8 x 1) वर्ग इकाई
= (6 + 8) वर्ग इकाई
= 14 वर्ग इकाई.
(n) पूर्ण वर्गों की संख्या = 9
आधे से अधिक वर्गों की संख्या = 9
∴ ढकी हुई आकृति का क्षेत्रफल
= (9 x 1 + 9 x 1) वर्ग इकाई
= (9 + 9) वर्ग इकाई = 18 वर्ग इकाई.
Ex 10.3
प्रश्न 1.
उन आयतों का क्षेत्रफल ज्ञात कीजिए जिनकी भुजाएँ हैं:
(a) 3 सेमी और 4 सेमी
(b) 12 मीटर और 21 मीटर
(c) 2 किमी और 3 किमी
(d) 2 मीटर और 70 सेमी
हल:
(a) आयत की लंबाई = 3 सेमी
आयत की चौड़ाई = 4 सेमी
∴ आयत का क्षेत्रफल = लंबाई x चौड़ाई = 3 सेमी x 4 सेमी
= 12 सेमी 2 या 12 वर्ग सेमी
(b) आयत की लंबाई = 12 मीटर और चौड़ाई = 21 मीटर
∴ आयत का क्षेत्रफल = लंबाई x चौड़ाई = 12 मीटर x 21 मीटर
= 252 मीटर 2 या 252 वर्ग मीटर
(c) आयत की लंबाई = 2 किमी और चौड़ाई 3 किमी
∴ आयत का क्षेत्रफल = लंबाई x चौड़ाई = 2 किमी x 3 किमी
= 6 किमी 2 या 6 वर्ग किमी
(d) आयत की लंबाई = 2 मीटर
और चौड़ाई = 70 सेमी या 0.70 मीटर
∴ आयत का क्षेत्रफल = लंबाई x चौड़ाई = 2 मीटर x 0.70 मीटर
= 1.40 मीटर 2 या 1.40 वर्ग मीटर
प्रश्न 2.
उन वर्गों का क्षेत्रफल ज्ञात कीजिए जिनकी भुजाएँ हैं:
(a) 10 सेमी
(b) 14 सेमी
(c) 5 मीटर
हल:
(a) वर्ग की भुजा = 10 सेमी
∴ वर्ग का क्षेत्रफल = भुजा x भुजा = 10 सेमी x 10 सेमी = 100 सेमी 2 या 100 वर्ग सेमी
(b) वर्ग की भुजा = 14 सेमी
∴ वर्ग का क्षेत्रफल = भुजा x भुजा = 14 सेमी x 14 सेमी = 196 सेमी 2 या 196 वर्ग सेमी
(c) वर्ग की भुजा = 5 मीटर
∴ वर्ग का क्षेत्रफल = भुजा x भुजा = 5 मीटर x 5 मीटर = 25 मीटर 2 या 25 वर्ग मीटर
प्रश्न 3.
तीन आयतों की लंबाई और चौड़ाई नीचे दी गई है:
(a) 9 मीटर और 6 मीटर
(b) 17 मीटर और 3 मीटर
(c) 4 मीटर और 14 मीटर
किसका क्षेत्रफल सबसे बड़ा है और किसका सबसे छोटा?
हल:
(a) आयत की लंबाई = 9 मीटर
और चौड़ाई = 6 मीटर
∴ आयत का क्षेत्रफल = लंबाई x चौड़ाई
= 9 मीटर x 6 मीटर
= 54 मीटर 2 या 54 वर्ग मीटर
(b) आयत की लंबाई = 17 मीटर
और चौड़ाई = 3 मीटर
∴ आयत का क्षेत्रफल
= लंबाई x चौड़ाई = 17 मीटर x 3 मीटर 51 मीटर 2 या 51 वर्ग मीटर
(c) आयत की लंबाई = 4 मीटर
और चौड़ाई = 14 मीटर
आयत का क्षेत्रफल = लंबाई x चौड़ाई
= 4 मीटर x 14 मीटर
= 56 मीटर 2 या 56 वर्ग मीटर
आयत (c) का क्षेत्रफल सबसे बड़ा है, अर्थात 56 वर्ग मीटर और आयत (b) का क्षेत्रफल सबसे छोटा है, अर्थात 51 वर्ग मीटर।
प्रश्न 4.
50 मीटर लंबे एक आयताकार बगीचे का क्षेत्रफल 300 वर्ग मीटर है। बगीचे की चौड़ाई ज्ञात कीजिए।
हल:
आयताकार बगीचे की लंबाई = 50 मीटर
आयताकार बगीचे का क्षेत्रफल = 300 वर्ग मीटर
∴ चौड़ाई = क्षेत्रफल ÷ लंबाई
= 300 वर्ग मीटर ÷ 50 मीटर = 6 मीटर
अतः बगीचे की चौड़ाई = 6 मीटर।
प्रश्न 5.
500 मीटर लंबे और 200 मीटर चौड़े एक आयताकार भूखंड पर ₹8 प्रति सौ वर्ग मीटर की दर से टाइल लगाने की लागत क्या है?
हल:
आयताकार भूखंड की लंबाई = 500 मीटर
और चौड़ाई = 200 मीटर
∴ भूखंड का क्षेत्रफल = लंबाई x चौड़ाई = 500 मीटर x 200 मीटर = 100000 वर्ग मीटर
अब भूखंड पर टाइल लगाने की दर = ₹8 प्रति 100 वर्ग मीटर
बगीचे पर टाइल लगाने की लागत = ₹(\(\frac { 8 }{ 100 }\)x 100000 ) = ₹8000 अतः आवश्यक लागत = ₹8000
प्रश्न 6.
एक टेबलटॉप का माप 2 मीटर x 1 मीटर 50 सेमी है। इसका क्षेत्रफल वर्ग मीटर में क्या है?
हल:
टेबलटॉप की लंबाई = 2 मीटर
और चौड़ाई = 1 मीटर 50 सेमी या 1.50 मीटर
∴ टेबलटॉप का क्षेत्रफल = लंबाई x चौड़ाई
= 2 मीटर x 1.50 मीटर
= 3 मीटर 2 या 3 वर्ग मीटर
अतः, टेबलटॉप का क्षेत्रफल = 3 वर्ग मीटर।
प्रश्न 7.
एक कमरा 4 मीटर लंबा और 3 मीटर 50 सेमी चौड़ा है। कमरे के फर्श को ढकने के लिए कितने वर्ग मीटर कालीन की आवश्यकता होगी?
हल:
कमरे की लंबाई = 4 मीटर
और चौड़ाई = 3 मीटर 50 सेमी = 3.5 मीटर
कमरे का क्षेत्रफल = लंबाई x चौड़ाई
= 4 मीटर x 3.5 मीटर = 14 वर्ग मीटर
अतः, आवश्यक कालीन का क्षेत्रफल = 14 वर्ग मीटर
प्रश्न 8.
एक फर्श 5 मीटर लंबा और 4 मीटर चौड़ा है। फर्श पर 3 मीटर भुजाओं वाला एक वर्गाकार कालीन बिछा हुआ है। उस फर्श का क्षेत्रफल ज्ञात कीजिए जिस पर कालीन नहीं है।
हल:
फर्श की लंबाई = 5 मीटर
और इसकी चौड़ाई = 4 मीटर
∴ फर्श का क्षेत्रफल = लंबाई x चौड़ाई
= 5 मीटर x 4 मीटर = 20 वर्ग मीटर
कालीन की भुजा = 3 मीटर
∴ वर्गाकार कालीन का क्षेत्रफल = भुजा x भुजा = 3 मीटर x 3 मीटर = 9 वर्ग मीटर
∴ उस फर्श का क्षेत्रफल जिस पर कालीन नहीं है = 20 वर्ग मीटर - 9 वर्ग मीटर
= 11 वर्ग मीटर
प्रश्न 9.
5 मीटर लंबे और 4 मीटर चौड़े एक भूखंड पर 1 मीटर भुजा वाली पांच वर्गाकार फूलों की क्यारियां खोदी गई हैं। शेष भूखंड का क्षेत्रफल क्या है?
हल:
वर्गाकार फूलों की क्यारी की भुजा = 1 मीटर।
∴ 1 वर्गाकार फूलों की क्यारी का क्षेत्रफल = 1 मीटर x 1 मीटर = 1 वर्ग मीटर।
∴ 5 वर्गाकार फूलों की क्यारियों का क्षेत्रफल = 1 वर्ग मीटर x 5 = 5 वर्ग मीटर।
अब भूखंड की लंबाई = 5 मीटर
और चौड़ाई = 4 मीटर।
∴ भूखंड का क्षेत्रफल = लंबाई x चौड़ाई = 5 मीटर x 4 मीटर = 20 वर्ग मीटर।
∴ भूखंड के शेष भाग का क्षेत्रफल = 20 वर्ग मीटर - 5 वर्ग मीटर
= 15 वर्ग मीटर।
प्रश्न 10.
निम्नलिखित आकृतियों को आयतों में विभाजित करके, उनके क्षेत्रफल ज्ञात कीजिए (माप सेंटीमीटर में दिए गए हैं)।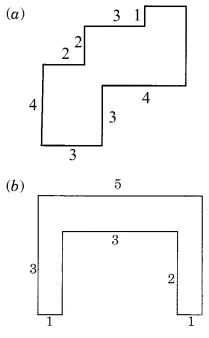
हल: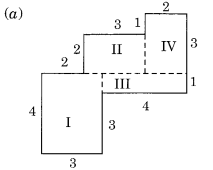
दी गई आकृति को आयत I, II, III और IV में विभाजित करने पर, हमें प्राप्त होता है
आयत I का क्षेत्रफल = लंबाई x चौड़ाई
= 4 सेमी x 3 सेमी = 12 वर्ग सेमी
आयत II का क्षेत्रफल = लंबाई x चौड़ाई
= 3 सेमी x 2 सेमी = 6 वर्ग सेमी
आयत III का क्षेत्रफल = लंबाई x चौड़ाई
= 4 सेमी x 1 सेमी = 4 वर्ग सेमी
आयत IV का क्षेत्रफल = लंबाई x चौड़ाई
= 3 सेमी x 2 सेमी = 6 वर्ग सेमी
∴ पूरी आकृति का कुल क्षेत्रफल
= 12 वर्ग सेमी + 6 वर्ग सेमी + 4 वर्ग सेमी + 6 वर्ग सेमी
= 28 वर्ग सेमी
(b) दी गई आकृति को आयत I, II और III में विभाजित करने पर, हम पाते हैं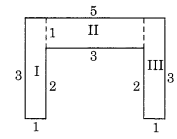
आयत I का क्षेत्रफल
= 12 सेमी x 2 सेमी = 24 वर्ग सेमी
आयत II का क्षेत्रफल
= 8 सेमी x 2 सेमी = 16 वर्ग सेमी
आयत III का क्षेत्रफल
= 3 सेमी x 1 सेमी = 3 वर्ग सेमी
∴ दी गई आकृति का कुल क्षेत्रफल = 3 वर्ग सेमी + 3 वर्ग सेमी + 3 वर्ग सेमी = 9 वर्ग सेमी।
प्रश्न 11.
निम्नलिखित आकृतियों को आयतों में विभाजित करें और उनके क्षेत्रफल ज्ञात करें (माप सेंटीमीटर में दिए गए हैं)।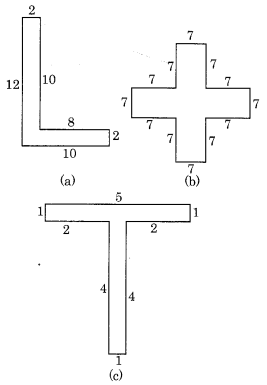
हल:
(a) दी गई आकृति को आयत I और II में विभाजित करने पर, हम पाते हैं कि
आयत I का क्षेत्रफल
= 12 सेमी x 2 सेमी = 24 वर्ग सेमी
आयत II का क्षेत्रफल
= 8 सेमी x 2 सेमी = 16 वर्ग सेमी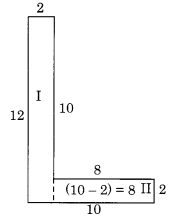
∴ पूरी आकृति का कुल क्षेत्रफल = 24 वर्ग सेमी + 16 वर्ग सेमी = 40 वर्ग सेमी।
(b) दी गई आकृति को आयत I, II और III में विभाजित करने पर, हम पाते हैं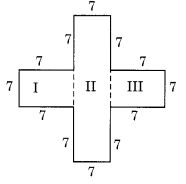
आयत I का क्षेत्रफल
= 7 सेमी x 7 सेमी = 49 वर्ग सेमी
आयत II का क्षेत्रफल
= 21 सेमी x 7 सेमी = 147 वर्ग सेमी
आयत III का क्षेत्रफल
= 7 सेमी x 7 सेमी = 49 वर्ग सेमी
∴ पूरी आकृति का कुल क्षेत्रफल
= 49 वर्ग सेमी + 147 वर्ग सेमी + 49 वर्ग सेमी
= 245 वर्ग सेमी।
प्रश्न 12.
एक आयताकार क्षेत्र जिसकी लंबाई और चौड़ाई क्रमशः 12 सेमी और 5 सेमी है, में फिट होने के लिए कितनी टाइलों की आवश्यकता होगी:
(a) 100 सेमी और 144 सेमी
(b) 70 सेमी और 36 सेमी
हल:
एक टाइल की लंबाई = 12 सेमी
टाइल की चौड़ाई = 5 सेमी
∴ 1 टाइल का क्षेत्रफल = लंबाई x चौड़ाई = 12 सेमी x 5 सेमी = 60 वर्ग सेमी
(a) आयताकार क्षेत्र की लंबाई = 144 सेमी
क्षेत्र की चौड़ाई = 100 सेमी
∴ आयताकार क्षेत्र का क्षेत्रफल = लंबाई x चौड़ाई = 144 सेमी x 100 सेमी
= 14400 वर्ग सेमी
∴ पूरे आयताकार क्षेत्र को ढकने के लिए आवश्यक टाइलों की संख्या
= 14400 वर्ग सेमी ÷ 60 वर्ग सेमी
= 240 टाइलें
(b) आयताकार क्षेत्र की लंबाई = 70 सेमी
क्षेत्र की चौड़ाई = 36 सेमी
∴ आयताकार क्षेत्र का क्षेत्रफल = लंबाई x चौड़ाई = 70 सेमी x 36 सेमी = 2520 वर्ग सेमी
∴ पूरे आयताकार क्षेत्र को कवर करने के लिए आवश्यक टाइलों की संख्या
= 2520 वर्ग सेमी ÷ 60 वर्ग सेमी
= 42 टाइलें।
InText Questions
लघु उत्तरीय प्रश्न
प्रश्न 1.
एक आयत की लंबाई ज्ञात कीजिए, जिसका परिमाप 880 मीटर और चौड़ाई 88 मीटर है।
हल:
आयत का परिमाप = 2 [लंबाई + चौड़ाई]
∴ 2 [लंबाई + चौड़ाई] = 880
लंबाई + चौड़ाई = 880 ÷ 2 = 440
∵ चौड़ाई = 88 मीटर
∴ लंबाई = 440 मीटर - 88 मीटर = 352 मीटर
इसलिए, आवश्यक लंबाई = 352 मीटर।
प्रश्न 2.
एक आयताकार भूखंड जिसकी लंबाई 120 मीटर और चौड़ाई 90 मीटर है, के चारों ओर 6 मीटर की दूरी पर कितने पेड़ लगाए जा सकते हैं?
हल:
आयताकार भूखंड की लंबाई = 120 मीटर
चौड़ाई = 90 मीटर
∴ आयताकार भूखंड का परिमाप
= 2 [लंबाई + चौड़ाई]
= 2 [120 मीटर + 90 मीटर]
= 2 x 210 मीटर = 420 मीटर
अब दो पेड़ों के बीच की दूरी = 6 मीटर
∴ आयताकार भूखंड के चारों ओर पेड़ों की संख्या = 420 मीटर ÷ 6 मीटर = 70
प्रश्न 3.
एक आयताकार पार्क 30 मीटर लंबा और 20 मीटर चौड़ा है। इसके चारों ओर स्टील के तार की बाड़ लगाई गई है। ₹15 प्रति मीटर की दर से बाड़ लगाने की लागत ज्ञात कीजिए।
हल:
आयताकार पार्क की लंबाई = 30 मीटर
चौड़ाई = 20 मीटर
∴ आयताकार पार्क का परिमाप = 2(लंबाई + चौड़ाई)
= 2 [30 + 20] = 2 x 50 मीटर = 100 मीटर
∴ पार्क के चारों ओर बाड़ लगाने की लागत = ₹15 x 100 = ₹1500
प्रश्न 4.
निम्नलिखित आकृति में, वर्गाकार कागज़ पर खींची गई आकृतियों A, B, C और D का क्षेत्रफल वर्गों की गिनती करके ज्ञात कीजिए।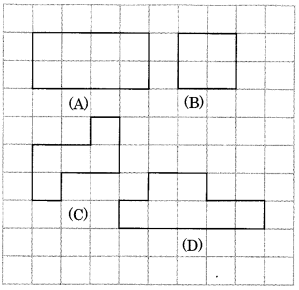
हल:
(A) वर्गों की गिनती करने पर, हमारे पास 8 वर्ग हैं
∴ क्षेत्रफल = 8 वर्ग इकाई
(B) वर्गों की गिनती करने पर, हमारे पास 4 वर्ग हैं
∴ क्षेत्रफल = 4 वर्ग इकाई
(C) वर्गों की गिनती करने पर, हमारे पास 5 वर्ग हैं
∴ क्षेत्रफल = 5 वर्ग इकाई
(D) वर्गों की गिनती करने पर, हमारे पास 7 वर्ग हैं
∴ क्षेत्रफल = 7 वर्ग इकाई
अति लघु उत्तरीय प्रश्न
प्रश्न 1.
एक वर्ग का परिमाप 64 सेमी है। प्रत्येक भुजा की लंबाई ज्ञात कीजिए।
हल:
वर्ग का परिमाप = 64 सेमी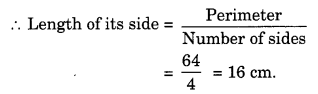
प्रश्न 2.
एक आयताकार टेबल-टॉप की लंबाई और चौड़ाई क्रमशः 36 सेमी और 24 सेमी है। इसका परिमाप ज्ञात कीजिए।
हल:
आयताकार टेबल-टॉप की लंबाई = 36 सेमी
और चौड़ाई = 24 सेमी।
∴ टेबल-टॉप का परिमाप = 2 [लंबाई + चौड़ाई]
= 2 [36 सेमी + 24 सेमी]
= 2 x 60 सेमी = 120 सेमी।
प्रश्न 3.
निम्नलिखित में से किस आकृति का परिमाप अधिक है?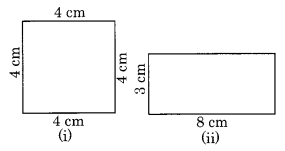
हल:
आकृति (i) वर्ग का परिमाप = 4 x भुजा
= 4 x 4 सेमी = 16 सेमी
आकृति (ii) आयत का परिमाप
= 2 [लंबाई + चौड़ाई]
= 2 [8 सेमी + 3 सेमी]
= 2 x 11 सेमी = 22 सेमी
चूँकि 22 सेमी > 16 सेमी
∴ आयत का परिमाप वर्ग से अधिक है।
प्रश्न 4.
निम्नलिखित प्रत्येक आकृति के चारों ओर घूमने में आपको कितनी दूरी तय करनी होगी?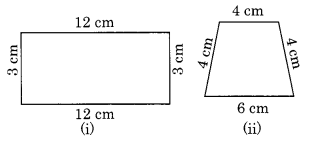
हल:
आकृति (i) के चारों ओर घूमने में तय की गई दूरी
= 12 सेमी + 3 सेमी + 12 सेमी + 3 सेमी = 30 सेमी
आकृति (ii) के चारों ओर घूमने में तय की गई दूरी
= 6 सेमी + 4 सेमी + 4 सेमी + 4 सेमी = 18 सेमी
प्रश्न 5.
एक वर्ग का परिमाप ज्ञात कीजिए जिसकी भुजा 15 सेमी है।
हल:
वर्ग की भुजा = 15 सेमी
∴ वर्ग का परिमाप = 15 सेमी x 4 = 60 सेमी
प्रश्न 6.
300 मीटर लंबे और 200 मीटर चौड़े एक आयताकार पार्क के चारों ओर ₹4 प्रति मीटर की दर से बाड़ लगाने की लागत ज्ञात कीजिए।
हल:
पार्क की लंबाई = 300 मीटर
चौड़ाई = 200 मीटर
∴ पार्क का परिमाप = 2 [लंबाई + चौड़ाई]
= 2 [300 मीटर + 200 मीटर]
= 2 x 500 मीटर = 1000 मीटर।
आयताकार पार्क के चारों ओर बाड़ लगाने की लागत = 1000 x 4 = ₹4000
प्रश्न 7.
एक वर्गाकार मैदान का क्षेत्रफल ज्ञात कीजिए जिसकी प्रत्येक भुजा 150 मीटर है।
हल:
वर्गाकार मैदान की भुजा = 150 मीटर
∴ वर्गाकार मैदान का क्षेत्रफल = भुजा x भुजा
= 150 मीटर x 150 मीटर
= 22500 वर्ग मीटर।
प्रश्न 8.
एक आयताकार कागज़ की लंबाई और चौड़ाई क्रमशः 22 सेमी और 10 सेमी है। कागज़ का क्षेत्रफल ज्ञात कीजिए।
हल:
आयताकार कागज़ की लंबाई = 22 सेमी
चौड़ाई = 10 सेमी
∴ आयताकार कागज़ का क्षेत्रफल = लंबाई x चौड़ाई
= 22 सेमी x 10 सेमी
= 220 वर्ग सेमी।
उच्च क्रम चिंतन कौशल (HOTS)
प्रश्न 1.
एक आयत और एक वर्ग का परिमाप समान 100 सेमी है। वर्ग की भुजा ज्ञात कीजिए। यदि आयत की चौड़ाई वर्ग की चौड़ाई से 2 सेमी कम है। आयत की चौड़ाई, लंबाई और क्षेत्रफल ज्ञात कीजिए।
हल:
वर्ग का परिमाप = 100 सेमी
परिमाप 100![]()
= 25 सेमी।
∴ आयत की चौड़ाई = 25 सेमी - 2 सेमी = 23 सेमी
अब आयत का परिमाप = 100 सेमी
∴ 2 [लंबाई + चौड़ाई] = 100
लंबाई + चौड़ाई = 100 ÷ 2 = 50 सेमी
लेकिन चौड़ाई = 23 सेमी
∴ लंबाई = 50 सेमी - 23 सेमी = 27 सेमी
अब, आयत का क्षेत्रफल
= लंबाई x चौड़ाई = 27 सेमी x 23 सेमी
= 621 वर्ग सेमी।
प्रश्न 2.
एक घर के परिसर में बाड़ लगाने की लागत ₹5452 है। यदि दर ₹94 प्रति मीटर है, तो परिसर का परिमाप ज्ञात कीजिए। यदि चौड़ाई 10 मीटर है, तो इसकी लंबाई ज्ञात कीजिए।
हल:
परिसर में बाड़ लगाने की लागत = ₹5452
और बाड़ लगाने की दर = ₹94 प्रति मीटर
∴ परिसर का परिमाप = 5452 ÷ 94 = 58 मीटर
अब परिसर की चौड़ाई = 10 मीटर।
2 [लंबाई + चौड़ाई] = 58 मीटर
∴ लंबाई + चौड़ाई = 58 + 2 मीटर = 29 मीटर
∴ परिसर की लंबाई = 29 मीटर - 10 मीटर = 19 मीटर
