SikhLo - Current Affairs in Hindi, Daily current affairs, Current affairs

 NCERT Class 7 Maths Chapter 3 आँकड़ों का प्रबंधन

NCERT Solutions for Class 7 Maths Chapter 3 आँकड़ों का प्रबंधन

Ex 3.1

प्रश्न 1.
अपनी कक्षा के किन्हीं दस विद्यार्थियों की ऊँचाइयों का परिसर ज्ञात कीजिए।
हल:
मान लीजिए कक्षा के 10 विद्यार्थियों की ऊँचाइयाँ (सेमी में) 150, 152, 151, 148, 149, 149, 150, 152, 153, 146 हैं।
ऊँचाइयों को आरोही क्रम में व्यवस्थित करने पर, हमें 146, 148, 149, 149, 150, 150, 151, 152, 152, 153 प्राप्त होते हैं।
विद्यार्थियों की ऊँचाइयों का परिसर = 153 – 146 = 7

प्रश्न 2.
कक्षा मूल्यांकन में निम्नलिखित अंकों को सारणीबद्ध रूप में व्यवस्थित करें।
4, 6, 7, 5, 3, 5, 4, 5, 2, 6, 2, 5, 1, 9, 6, 5, 8, 4, 6, 7
(i) कौन सी संख्या सबसे बड़ी है?
(ii) कौन सी संख्या सबसे छोटी है?
(iii) आँकड़ों का परिसर क्या है?
(iv) अंकगणितीय माध्य ज्ञात कीजिए।
हल:

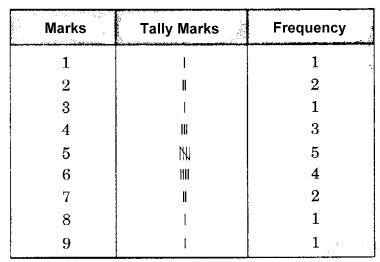
(i) सबसे बड़ी संख्या 9 है।
(ii) सबसे छोटी संख्या 1 है।
(iii) आँकड़ों का परिसर = सबसे बड़ा अवलोकन - सबसे छोटा अवलोकन
= 9 - 1
= 8

प्रश्न 3.
प्रथम पाँच पूर्ण संख्याओं का माध्य ज्ञात कीजिए।
हल:
प्रथम 5 पूर्ण संख्याएँ 0, 1, 2, 3 और 4 हैं।
उनका समांतर माध्य

प्रश्न 4.
एक क्रिकेटर आठ पारियों में निम्नलिखित रन बनाता है:
58, 76, 40, 35, 46, 45, 0, 100.
औसत स्कोर ज्ञात कीजिए।
हल:

प्रश्न 5.
निम्नलिखित तालिका चार खेलों में प्रत्येक खिलाड़ी द्वारा बनाए गए अंक दर्शाती है: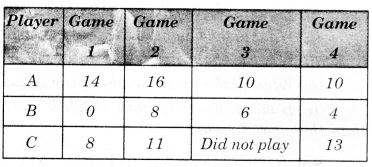

अब निम्नलिखित प्रश्नों के उत्तर दीजिए:

1. प्रति खेल A द्वारा बनाए गए औसत अंकों की संख्या ज्ञात करने के लिए माध्य ज्ञात कीजिए।
2. C के प्रति खेल औसत अंक ज्ञात करने के लिए, क्या आप कुल अंकों को 3 से भाग देंगे या 4 से? क्यों?
3. B ने चारों खेलों में खेला। आप माध्य कैसे ज्ञात करेंगे?
4. सबसे अच्छा प्रदर्शन कौन करता है?

हल:

अतः, A द्वारा प्रति खेल में बनाए गए अंकों की औसत संख्या 12.5 है।
(ii) C के लिए प्रति खेल अंकों की औसत संख्या ज्ञात करने के लिए, हम कुल अंकों को 3 से भाग देंगे क्योंकि विचाराधीन खेलों की संख्या 4 है लेकिन 'C' ने खेल 3 नहीं खेला।

प्रश्न 6.
विज्ञान की परीक्षा में छात्रों के एक समूह द्वारा प्राप्त अंक (100 में से) 85, 76, 90, 85, 39, 48, 56, 95, 81 और 75 हैं। ज्ञात कीजिए:

1. छात्रों द्वारा प्राप्त उच्चतम एवं न्यूनतम अंक।
2. प्राप्त अंकों की सीमा.
3. समूह द्वारा प्राप्त औसत अंक.

समाधान:

1. छात्रों द्वारा प्राप्त उच्चतम अंक = 95
   छात्रों द्वारा प्राप्त न्यूनतम अंक = 39
2. प्राप्त अंकों की सीमा = उच्चतम अंक – न्यूनतम अंक = 95 – 39 = 56
3. समूह द्वारा प्राप्त औसत अंक
   

प्रश्न 7.
छह क्रमागत वर्षों के दौरान एक स्कूल में नामांकन इस प्रकार था:
1555, 1670, 1750, 2013, 2540, 2820।
इस अवधि के लिए स्कूल में नामांकन का माध्य ज्ञात कीजिए।
हल:
इस अवधि के लिए स्कूल में नामांकन का माध्य।

प्रश्न 8.
एक शहर में एक निश्चित सप्ताह के 7 दिनों में वर्षा (मिमी में) निम्नानुसार दर्ज की गई:

(i)  उपरोक्त आँकड़ों में वर्षा का परिसर ज्ञात कीजिए।
(ii) सप्ताह के लिए औसत वर्षा ज्ञात कीजिए।
(iii) कितने दिनों में वर्षा औसत वर्षा से कम थी?
हल:
(i) वर्षा का परिसर = अधिकतम वर्षा - न्यूनतम वर्षा = 20.5 मिमी - 0.0 मिमी = 20.5 मिमी
(ii) सप्ताह के लिए औसत वर्षा

(iii) 5 दिनों में वर्षा औसत वर्षा से कम थी।

प्रश्न 9.
10 लड़कियों की ऊँचाई सेमी में मापी गई और परिणाम इस प्रकार हैं:
135, 150, 139, 128, 151, 132, 146, 149, 143, 141.
(i) सबसे लंबी लड़की की ऊँचाई क्या है?
(i) सबसे छोटी लड़की की ऊँचाई क्या है?
(iii) आँकड़ों की सीमा क्या है?
(iv) लड़कियों की औसत ऊँचाई क्या है?
(v) कितनी लड़कियों की ऊँचाई औसत ऊँचाई से अधिक है?

हल:
(i) सबसे लंबी लड़की की ऊंचाई = 151 सेमी
(ii) सबसे छोटी लड़की की ऊंचाई = 128 सेमी
(iii) डेटा की सीमा

(v) 5 लड़कियों की ऊंचाई औसत ऊंचाई से अधिक है।

Ex 3.2

प्रश्न 1.
15 छात्रों के गणित परीक्षण में अंक (25 में से) इस प्रकार हैं:
19, 25, 23, 20, 9, 20, 15, 10, 5, 16, 25, 20, 24, 12, 20
इस डेटा का बहुलक और माध्यिका ज्ञात कीजिए। क्या वे समान हैं?
समाधान:
माध्यिका के लिए। हम डेटा को आरोही क्रम में व्यवस्थित करते हैं, हम पाते हैं
5, 9, 10, 12, 15, 16, 19, 20,
20, 20, 20, 23, 24, 25, 25
माध्यिका मध्य अवलोकन है।
इसलिए, 20 माध्यिका है।
बहुलक के लिए।
बहुलक = उच्चतम आवृत्ति वाला अवलोकन = 20
हां, वे समान हैं।

प्रश्न 2.
एक क्रिकेट मैच में 11 खिलाड़ियों द्वारा बनाए गए रन इस प्रकार हैं:
6, 15, 120, 50, 100, 80, 10, 15, 8, 10, 15.
इन आँकड़ों का माध्य, बहुलक और माध्यिका ज्ञात कीजिए। क्या ये तीनों समान हैं?
हल:

(ii) माध्यिका के लिए। हम आँकड़ों को आरोही क्रम में व्यवस्थित करते हैं, हमें
6, 8, 10, 10, 15, 15, 15, 50, 80, 100, 120
हैं। माध्यिका मध्य का अवलोकन है। इसलिए, 15 माध्यिका है।

(iii) बहुलक के लिए। बहुलक = उच्चतम आवृत्ति वाला प्रेक्षण = 15
नहीं! ये समान नहीं हैं।

प्रश्न 3.
एक कक्षा के 15 छात्रों का वजन (किलोग्राम में) है:
38, 42, 35, 37, 45, 50, 32, 43,
43, 40, 36, 38, 43, 38, 47

1. इस डेटा का बहुलक और माध्यिका ज्ञात कीजिए।
2. क्या एक से अधिक मोड हैं?

हल:
(i) माध्यिका के लिए। हम आँकड़ों को आरोही क्रम में व्यवस्थित करते हैं, हमें
32, 35, 36, 37, 38, 38, 38, 40, 42, 43, 43,
43, 45, 47, 50
होते हैं। माध्यिका मध्य का प्रेक्षण है।
अतः, 40 किग्रा माध्यिका है।
बहुलक के लिए। बहुलक = उच्चतम आवृत्ति वाला प्रेक्षण = 38 किग्रा और 43 किग्रा।
(ii) हाँ! दो (एक से अधिक) बहुलक हैं।

प्रश्न 4.
आँकड़ों का बहुलक और माध्यिका ज्ञात कीजिए:
13, 16, 12, 14, 19, 12, 14, 13, 14.
हल:
माध्यिका के लिए, हम आँकड़ों को आरोही क्रम में व्यवस्थित करते हैं, हमें 12, 12, 13, 13, 14, 14, 14, 16, 19 प्राप्त होते हैं।
माध्यिका मध्य का प्रेक्षण है।
अतः, 14 माध्यिका है।
बहुलक के लिए, बहुलक = उच्चतम आवृत्ति वाला प्रेक्षण = 14.

प्रश्न 5.
बताइये कि कथन सत्य है या असत्य:

1. बहुलक सदैव डेटा में से एक संख्या होती है।
2. माध्य, आँकड़ों में से एक संख्या है।
3. माध्यिका सदैव डेटा में से एक संख्या होती है।
4. डेटा 6, 4, 3, 8, 9, 12, 13, 9 का माध्य 9 है।

समाधान:

1. सत्य
2. असत्य
3. सत्य
4. असत्य।

Ex 3.3

प्रश्न 1.
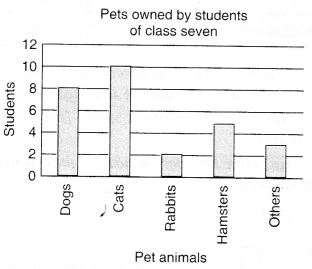
निम्नलिखित प्रश्नों के उत्तर देने के लिए दंड आलेख का प्रयोग कीजिए।
(a) सबसे लोकप्रिय पालतू जानवर कौन सा है?
(b) कितने बच्चों के पास पालतू जानवर के रूप में कुत्ता है?

हल:
(a) सबसे लोकप्रिय पालतू जानवर 'बिल्ली' है।
(b) 8 बच्चों के पास पालतू जानवर के रूप में कुत्ता है।

प्रश्न 2.
एक किताब की दुकान द्वारा लगातार पाँच वर्षों के दौरान बेची गई पुस्तकों की संख्या को दर्शाने वाले दंड आलेख को पढ़िए और निम्नलिखित प्रश्नों के उत्तर दीजिए: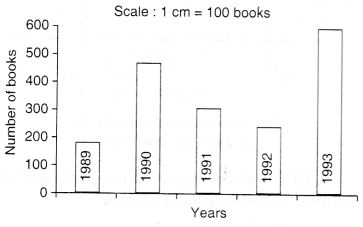

1. 1989, 1990, 1992 में लगभग कितनी किताबें बिकीं?
2. किस वर्ष लगभग 475 पुस्तकें बिकीं? लगभग 225 पुस्तकें बिकीं?
3. किन वर्षों में 250 से कम पुस्तकें बिकीं?
4. क्या आप बता सकते हैं कि 1989 में बेची गई पुस्तकों की संख्या का आप कैसे अनुमान लगाएंगे?

हल:
दिए गए ग्राफ से स्पष्ट है कि

1. वर्ष
   1989 में बेची गई पुस्तकों की संख्या: 170 (लगभग)
   1990: 475 (लगभग)
   1992: 225 (लगभग)
2. वर्ष 1990 में लगभग 475 पुस्तकें बिकीं। वर्ष 1992 में लगभग 225 पुस्तकें बिकीं।
3. वर्ष 1989 और 1992 में 250 से भी कम पुस्तकें बिकीं।
4. बार की ऊंचाई का उपयोग करके इसका अनुमान लगाया जा सकता है कि 1 सेमी की ऊंचाई = 100 पुस्तकें।

प्रश्न 3.
छह अलग-अलग कक्षाओं में बच्चों की संख्या नीचे दी गई है। आँकड़ों को एक दंड आलेख पर दर्शाइए।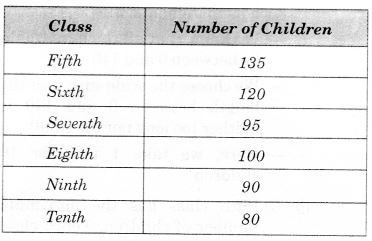

(a) आप पैमाना कैसे चुनेंगे?
(b) निम्नलिखित प्रश्नों के उत्तर दीजिए:
(i) किस कक्षा में बच्चों की संख्या सबसे अधिक है? और सबसे कम?
(ii) छठी कक्षा के छात्रों का आठवीं कक्षा के छात्रों से अनुपात ज्ञात कीजिए।
हल: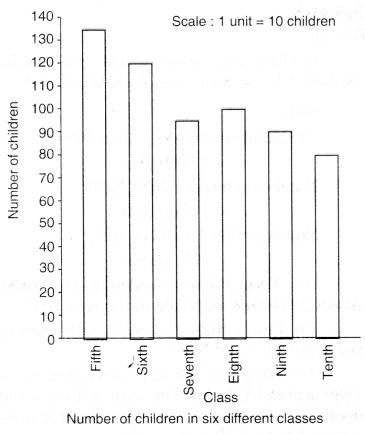

(a) पैमाना 0 से शुरू करें। आँकड़ों में सबसे बड़ा मान 135 है, इसलिए पैमाने को 135 से अधिक मान, जैसे 140, पर समाप्त करें। अक्षों के अनुदिश समान विभाजनों का प्रयोग करें, जैसे 10 की वृद्धि।
हम जानते हैं कि सभी बार 0 और 140 के बीच होंगे।

हम ऐसा पैमाना चुनते हैं जिससे 0 और 140 के बीच की लंबाई न तो बहुत लंबी हो और न ही बहुत छोटी।
यहाँ, हम 10 बच्चों के लिए 1 इकाई लेते हैं।
(b) (i) पाँचवीं कक्षा में बच्चों की संख्या सबसे अधिक है। दसवीं कक्षा में बच्चों की संख्या सबसे कम है।
(ii) छठी कक्षा के छात्रों का आठवीं कक्षा से अनुपात = 120 : 100 = \(\frac { 12 }{ 100 } \) = \(\frac { 6 }{ 5 } \) = 6 : 512100 = 65 = 6 : 5

प्रश्न 4.
एक विद्यार्थी का प्रथम सत्र और द्वितीय सत्र में प्रदर्शन दिया गया है। उपयुक्त पैमाना चुनकर दोहरा दंड आलेख खींचिए और निम्नलिखित प्रश्नों के उत्तर दीजिए: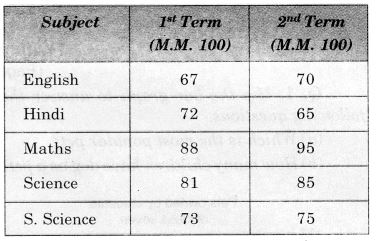

1. किस विषय में बच्चे ने अपने प्रदर्शन में सबसे अधिक सुधार किया है?
2. किस विषय में सुधार सबसे कम है?
3. क्या किसी विषय में प्रदर्शन में गिरावट आई है?

समाधान: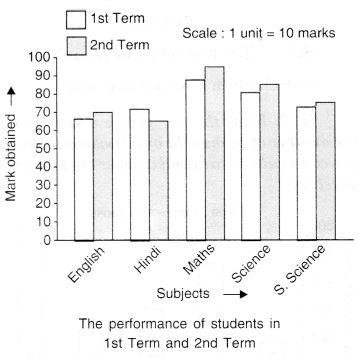

1. बच्चे ने गणित विषय में अपना प्रदर्शन सबसे अधिक सुधारा।
2. एस. विज्ञान विषय में सुधार सबसे कम है।
3. हाँ! हिंदी विषय में प्रदर्शन कम हुआ है।

प्रश्न 5.
एक कॉलोनी के सर्वेक्षण से एकत्रित इन आंकड़ों पर विचार करें।

1. उपयुक्त पैमाना चुनकर एक दोहरा ग्राफ़ बनाएँ।
   इस दंड ग्राफ़ से आप क्या निष्कर्ष निकालते हैं?
2. कौन सा खेल सबसे लोकप्रिय है?
3. कौन सा खेल अधिक पसंद किया जाता है, खेल देखना या उसमें भाग लेना?

समाधान: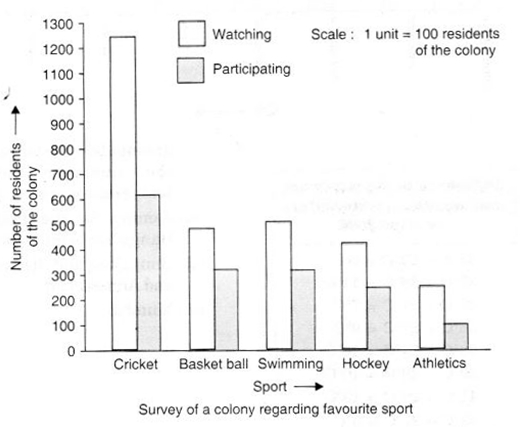

1. इससे यह अनुमान लगाया जा सकता है कि अधिक लोग क्रिकेट को पसंद करते हैं और कम लोग एथलेटिक्स को।
2. सबसे लोकप्रिय खेल क्रिकेट है।
3. भाग लेने की अपेक्षा देखना अधिक पसंद किया जाता है।

प्रश्न 6.
इस अध्याय के आरंभ में दिए गए विभिन्न शहरों के न्यूनतम और अधिकतम तापमान के आँकड़ों को लीजिए। आँकड़ों का उपयोग करके एक दोहरा दंड आलेख खींचिए और निम्नलिखित प्रश्नों के उत्तर दीजिए:

1. दी गई तिथि पर किस शहर के न्यूनतम और अधिकतम तापमान में सबसे अधिक अंतर है?
2. सबसे गर्म शहर कौन सा है और सबसे ठंडा शहर कौन सा है?
3. ऐसे दो शहरों के नाम बताइए जहां एक का अधिकतम तापमान दूसरे के न्यूनतम तापमान से कम था।
4. उस शहर का नाम बताइए जिसके न्यूनतम और अधिकतम तापमान के बीच सबसे कम अंतर है।

समाधान: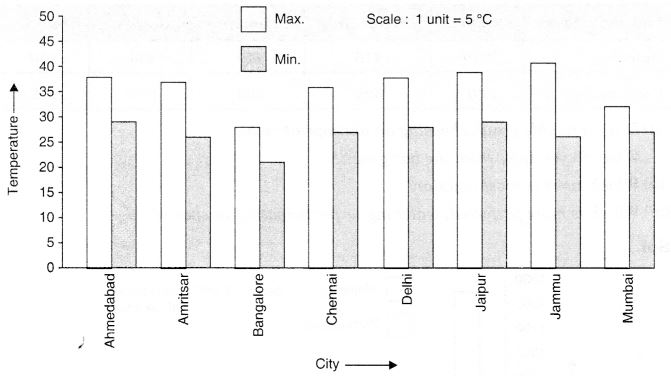

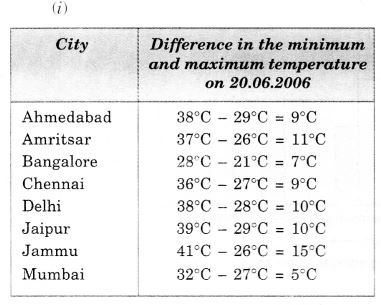
1. दी गई तिथि पर जम्मू शहर में न्यूनतम और अधिकतम तापमान में सबसे अधिक अंतर है।
2. जम्मू सबसे गर्म शहर है और बैंगलोर सबसे ठंडा शहर है।
3. उन दो शहरों का नाम, जहां एक का अधिकतम तापमान दूसरे के न्यूनतम तापमान से कम था, बैंगलोर और जयपुर या बैंगलोर और अहमदाबाद हैं।
4. मुंबई में न्यूनतम और अधिकतम तापमान के बीच सबसे कम अंतर है।

Ex 3.4

प्रश्न 1.
बताइये कि निम्नलिखित में से क्या घटित होना निश्चित है, असंभव है, हो सकता है परन्तु निश्चित नहीं है।

1. आज आप कल से अधिक उम्र के हैं।
2. उछाला गया सिक्का सिर ऊपर आएगा।
3. जब पासा उछाला जाएगा तो ऊपर 8 आएगा।
4. अगली ट्रैफिक लाइट हरी होगी।
5. कल बादल छाये रहेंगे।

समाधान:

1. निश्चित रूप से घटित होगा
2. हो सकता है लेकिन निश्चित नहीं
3. असंभव
4. हो सकता है लेकिन निश्चित नहीं
5. हो सकता है लेकिन निश्चित नहीं

प्रश्न 2.
एक बॉक्स में 6 कंचे हैं और प्रत्येक पर 1 से 6 तक संख्याएँ अंकित हैं।

1. संख्या 2 वाला कंचा निकालने की प्रायिकता क्या है?
2. संख्या 5 वाला कंचा निकालने की प्रायिकता क्या है?

हल:
6 कंचों में से एक कंचा 6 तरीकों से निकाला जा सकता है। इसलिए, घटनाओं की कुल संख्या = 6

1. संख्या 2 वाला कंचा केवल एक ही तरीके से प्राप्त किया जा सकता है।
∴ अभीष्ट प्रायिकता = \(\frac { 1 }{ 6 } \)16

प्रश्न 3.
कौन सी टीम खेल शुरू करेगी, यह तय करने के लिए एक सिक्का उछाला जाता है। आपकी टीम के खेल शुरू करने की क्या प्रायिकता है?
हल:
सिक्का उछालने पर, संभावित परिणाम चित (H) या पट (T) हैं।
अभीष्ट प्रायिकता = \(\frac { 1 }{ 2 } \)12