SikhLo - Current Affairs in Hindi, Daily current affairs, Current affairs

 NCERT Class 7 Maths Chapter 4 सरल समीकरण

NCERT Solutions for Class 7 Maths Chapter 4 सरल समीकरण

Ex 4.1

प्रश्न 1.
तालिका के अंतिम कॉलम को पूरा करें।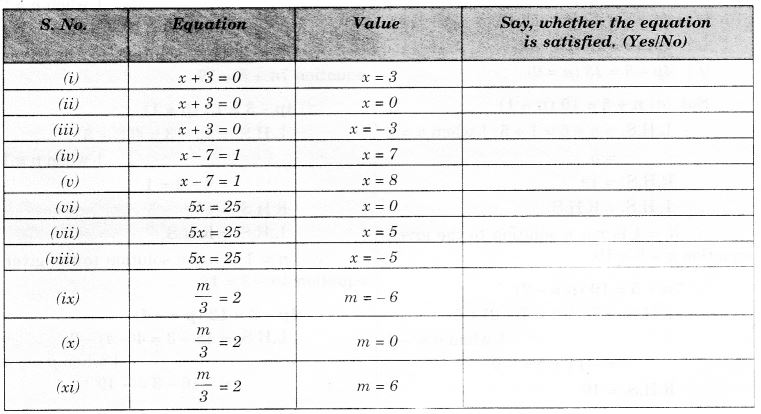

हल: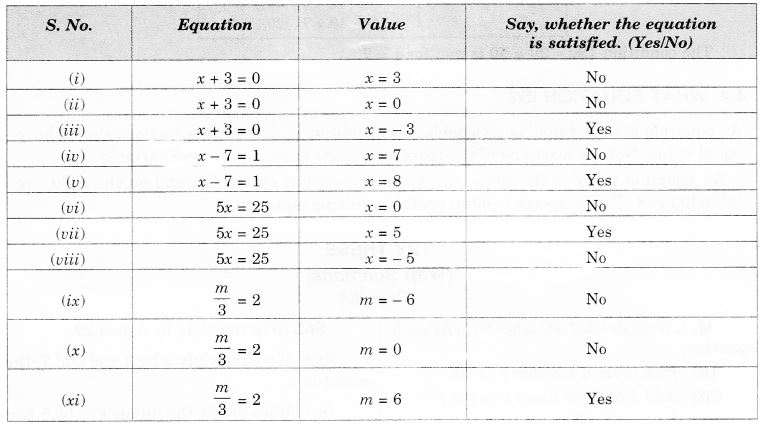

प्रश्न 2.
जाँच कीजिए कि कोष्ठक में दिया गया मान दिए गए समीकरण का हल है या नहीं।

(ए) एन + 5 = 19 (एन = 1)
(बी) 7एन + 5 = 19 (एन = - 2)
(सी) 7एन + 5 = 19 (एन = 2)
(डी) 4पी - 3 = 13 (पी = 1)
(ई) 4पी - 3 = 13 (पी = - 4)
(एफ) 4पी - 3 = 13 (पी = 0)।

हल:
(a) n + 5 = 19 (n = 1)
बायाँ पक्ष = n + 5 = 1 + 5 | जब n = 1 = 5
दायाँ पक्ष = 19
∵ बायाँ पक्ष ≠ दायाँ पक्ष
∴ n = 1 दिए गए समीकरण n + 5 = 19 का हल नहीं है।

(b) 7n + 5 = 19 (n = – 2)
बायाँ पक्ष = 7n + 5 = 7(- 2) + 5 | जब n = – 2 = – 14 + 5 = – 9
दायाँ पक्ष = 19
∵ बायाँ पक्ष ≠ दायाँ पक्ष
∴ n = – 2 दिए गए समीकरण 7n + 5 = 19 का हल नहीं है।

(c) 7n + 5 = 19 (n = 2)
बायाँ पक्ष = In + 5 = 7(2) + 5 | जब n = 2 = 14 + 5 = 19 = दायाँ पक्ष
∴ n = 2 दिए गए समीकरण 7n + 5 = 19 का हल है।

(d) 4p – 3 = 13 (p = 1)
बायाँ पक्ष = 4p – 3 = 4(1) – 3 | जब p = 1 = 4 – 3 = 1
दायाँ पक्ष = 13
∵ बायाँ पक्ष ≠ दायाँ पक्ष
∴ p = 1 दिए गए समीकरण 4p – 3 = 13 का हल नहीं है।

(e) 4p – 3 = 13 (p = – 4)
बायाँ पक्ष = 4p – 3 = 4(- 4) – 3, | जब p = – 4 = – 16 – 3 = – 19
दायाँ पक्ष = 13
∵ बायाँ पक्ष ≠ दायाँ पक्ष ∴ p = – 4 दिए गए समीकरण 4p – 3 = 13
का हल नहीं है ।

(f) 4p – 3 = 13 (p = 0)
बायाँ पक्ष = 4 (p) – 3 = 4(0) – 3 | जब p = 0 = 0 – 3 = – 3
दायाँ पक्ष = 13
∵ बायाँ पक्ष ≠ दायाँ पक्ष
∴ p = 0 दिए गए समीकरण 4p – 3 = 13 का हल नहीं है।

प्रश्न 3.
निम्नलिखित समीकरणों को परीक्षण और त्रुटि विधि से हल करें।

1. 5पी + 2 = 17
2. 3मी – 14 = 4.

हल:
(i) 5p + 2 = 17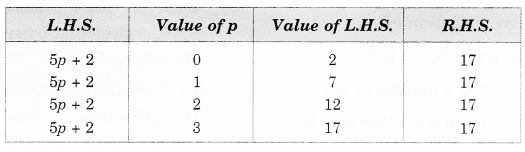

अतः, p = 3 दिए गए समीकरण 5p + 2 = 17 का हल है।

(ii) 3m – 14 = 4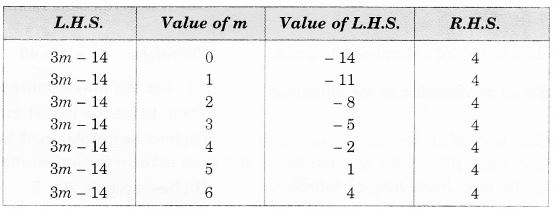

अतः, m = 6 दिए गए समीकरण 3m – 14 = 4 का हल है।

प्रश्न 4.
निम्नलिखित कथनों के लिए समीकरण लिखिए।

1. संख्या x और 4 का योग 9 है।
2. y में से 2 घटाने पर 8 आता है।
3. दस गुना a = 70.
4. संख्या b को 5 से भाग देने पर 6 प्राप्त होता है।
5. तीन-चौथाई बार 15 है।
6. सात गुणा m और 7 जोड़ने पर 77 प्राप्त होगा।
7. किसी संख्या x का एक-चौथाई - 4, 4 देता है।
8. यदि आप 6 गुणा y में से 6 घटा दें तो आपको 60 प्राप्त होगा।
9. यदि आप z के एक-तिहाई में 3 जोड़ते हैं, तो आपको 30 प्राप्त होता है।

समाधान:

1. x + 4 = 9
2. y – 2 = 8
3. 10 ए = 70
4. बी ÷ 5 = 6
5. 34 × t = 15
6. 7 मी + 7 = 77
7. 14 × x – 4 = 4
8. 6y – 6 = 60
9. 13 × z + 3 = 30

प्रश्न 5.
निम्नलिखित समीकरणों को कथन रूप में लिखिए:

1. पी + 4 = 15
2. मी – 7 = 3
3. 2मी = 7
4. m5 = 3
5. 3m5 = 6
6. 3पी + 4 = 25
7. 4पी – 2 = 18
8. p2 + 2 = 8.

समाधान:

1. p और 4 का योग 15 है।
2. m में से 7 घटाने पर 3 आता है।
3. संख्या m का दुगुना 7 होता है।
4. संख्या m का पांचवां भाग 3 है।
5. संख्या m का तीन-पांचवां भाग 6 है।
6. किसी संख्या p का तीन गुना 4 में जोड़ने पर 25 प्राप्त होता है।
7. किसी संख्या p के चार गुने में से 2 घटाने पर 18 प्राप्त होता है।
8. संख्या p के आधे भाग में 2 जोड़ने पर 8 प्राप्त होगा।

प्रश्न 6.
निम्नलिखित स्थितियों में समीकरण बनाइए:

1. इरफ़ान कहता है कि उसके पास परमिट के पास मौजूद कंचों की संख्या से पाँच गुना ज़्यादा 7 कंचे हैं। इरफ़ान के पास 37 कंचे हैं। (परमिट के कंचों की संख्या m लीजिए।)
2. लक्ष्मी के पिता 49 वर्ष के हैं। वह लक्ष्मी की आयु के तीन गुने से 4 वर्ष बड़े हैं। (लक्ष्मी की आयु y वर्ष मान लीजिए।)
3. शिक्षिका कक्षा को बताती है कि उसकी कक्षा में एक विद्यार्थी द्वारा प्राप्त अधिकतम अंक न्यूनतम अंक के दोगुने और 7 के योग के बराबर हैं। अधिकतम अंक 87 हैं। (निम्नतम अंक 1 लें।)
4. एक समद्विबाहु त्रिभुज में, शीर्ष कोण किसी भी आधार कोण का दोगुना होता है। (मान लीजिए कि आधार कोण b डिग्री में है। याद रखें कि त्रिभुज के कोणों का योग 180 डिग्री होता है)।

हल:
(i) मान लीजिए कि परमिट के पास कंचों की संख्या m है।
फिर, 5 गुना mis में 7 जोड़ने पर 5m + 7 आता है।
यह दिया गया है कि कंचे के पाँच गुने से 7 अधिक कंचे 37 हैं। इस प्रकार, प्राप्त समीकरण 5m + 7 = 37 है।

(ii) मान लीजिए लक्ष्मी की आयु y वर्ष है। y के 3 गुने में 4 जोड़ने पर 3y + 4 आता है।
यह दिया है कि पिता की आयु लक्ष्मी की आयु के 3 गुने से 4 वर्ष अधिक है। उनकी आयु 49 वर्ष है।
अतः, हमारे पास निम्नलिखित समीकरण है: 3y + 4 = 49

(iii) माना न्यूनतम अंक l हैं। तब, न्यूनतम अंकों का दोगुना + 7 = 2l + 7
यह दिया गया है कि, किसी छात्र द्वारा प्राप्त अधिकतम अंक 87, न्यूनतम अंकों का दोगुना + 7 है।
अतः, हमारे पास निम्नलिखित समीकरण है: 2l + 7 = 87

(iv) मान लीजिए आधार कोण b है। तब शीर्ष कोण = 2b है।
चूँकि त्रिभुज के कोणों का योग 180° होता है
∴ b + b + 2b = 180°
⇒ 4b = 180°
जो कि अभीष्ट समीकरण है।

Ex 4.2

प्रश्न 1.
सबसे पहले वह चरण बताइए जिसका उपयोग आप चर को अलग करने के लिए करेंगे और फिर समीकरण को हल करें:
(a) x – 1 = 0
(b) x + 1 = 0
(c) x – 1 = 5
(e) y – 4 = – 7
(f) y – 4 = 4
(g) y + 4 = 4
(h) y + 4 = – 4
हल:
(a) दिया गया समीकरण x – 1 = 0 है
दोनों पक्षों में 1 जोड़ें,
x – 1 + 1 = 0 + 1 ⇒ x = 1
यह अभीष्ट हल है।
जाँच करें। हल x = 1 को समीकरण में वापस डालें।
बायाँ पक्ष = x – 1 = 1 = 1 – 0 = दायाँ पक्ष
इस प्रकार हल की सत्यता की जाँच हो जाती है।

(b) दिया गया समीकरण x + 1 = 0 है।
दोनों पक्षों से 1 घटाने पर, x + 1 – 1 = 0 – 1 ⇒ x = – 1
यह अभीष्ट हल है।
जाँच कीजिए। हल x = – 1 को समीकरण में वापस रखिए।
बायाँ पक्ष = x + 1 = (-1)+1
= 0 = दायाँ पक्ष।
इस प्रकार, हल की सत्यता की जाँच हो जाती है।

(c) दिया गया समीकरण
x – 1 = 5 है
। दोनों पक्षों में 1 जोड़ने पर,
x + 1 – 1 = 5 + 1 ⇒ x = 6
यह अभीष्ट हल है
। जाँच कीजिए। हल x = 6 को समीकरण में वापस रखिए।
बायाँ पक्ष = x – 1 = 6 – 1 = 5 = दायाँ पक्ष।
इस प्रकार, हल की सत्यता की जाँच हो जाती है।

(d) दिया गया समीकरण x + 6 = 2 है।
दोनों पक्षों से 6 घटाने पर, x + 6 – 6 = 2 – 6 ⇒ x = – 4
यह अभीष्ट हल है।
जाँच कीजिए। हल x = – 4 को समीकरण में वापस रखिए।
बायाँ पक्ष = x + 6 = – 4 + 6 = 2 = दायाँ पक्ष।
इस प्रकार, हल की सत्यता की जाँच हो जाती है।

(e) दिया गया समीकरण y – 4 = – 7 है।
दोनों पक्षों में 4 जोड़ने पर, y – 4 + 4 = – 7 + 4 ⇒ y = – 3
यह अभीष्ट हल है।
जाँच कीजिए। हल को
बाएँ पक्ष में रखें = y – 4 = – 3 – 4 = – 7 = दाएँ पक्ष में।
इस प्रकार हल की सत्यता की जाँच हो जाती है।

(f) दिया गया समीकरण y – 4 = 4 है।
दोनों पक्षों में 4 जोड़ने पर,
y – 4 + 4 = 4 + 4 ⇒ y = 8
यह अभीष्ट हल है।
जाँच कीजिए। हल y = 8 को समीकरण में वापस रखिए।
बायाँ पक्ष = y – 4 = 8 – 4 = 4 = दायाँ पक्ष।
इस प्रकार, हल की सत्यता की जाँच हो जाती है।

(g) दिया गया समीकरण y + 4 = 4 है।
दोनों पक्षों से 4 घटाने पर, y + 4 – 4 = 4 – 4 ⇒ y = 0
यह अभीष्ट हल है।
जाँच कीजिए। हल y = 0 को समीकरण में वापस रखिए।
बायाँ पक्ष = y + 4 = 0 + 4 = 4 = दायाँ पक्ष।
इस प्रकार, हल की सत्यता की जाँच हो जाती है।

(h) दिया गया समीकरण y + 4 = – 4 है।
दोनों पक्षों से 4 घटाने पर, y + 4 – 4 = – 4 – 4 ⇒ y = -8
यह अभीष्ट हल है।
जाँच कीजिए। हल y = – 8 को समीकरण में वापस रखिए।
बायाँ पक्ष = y + 4 = -8 + 4 = – 4 = दायाँ पक्ष।
इस प्रकार, हल की सत्यता की जाँच हो जाती है।

प्रश्न 2.
सबसे पहले वह चरण बताइए जिसका उपयोग आप चर को अलग करने के लिए करेंगे और फिर समीकरण को हल करेंगे:
(a) 3l = 42
(b) \(\frac { b }{ 2 } \) = 6 (c) \(\frac { p }{ 7 } \) = 4 (d) 4x = 25 (e) 8y = 36 (f) \(\frac { z }{ 3 } \) = \(\frac { 5 }{ 4 } \) (g) \(\frac { a }{ 5 } \) = \(\frac { 7 }{ 15 } \) (h) 20t = – 10b2 = 6
p7 = 4
z3 = 54
a5 = 715

समाधान:

प्रश्न 3.
चर को अलग करने के लिए आप जिन चरणों का उपयोग करेंगे उन्हें बताएं और फिर समीकरण को हल करें:
(a) 3n ​​– 2 = 46
(b) 5m + 7 = 17
(c) \(\frac { 20p }{ 3 } \) = 40 (d) \(\frac { 3p }{ 10 } \) = 6 

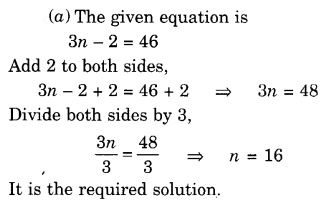
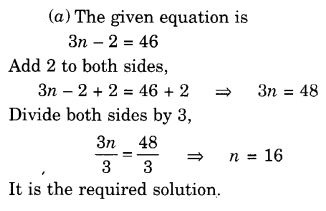
हल:20p3 = 40
3p10 = 6

प्रश्न 4.
निम्नलिखित समीकरणों को हल करें: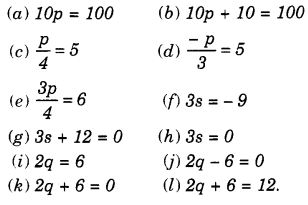

हल:

Ex 4.3

प्रश्न 1.
निम्नलिखित समीकरणों को हल करें: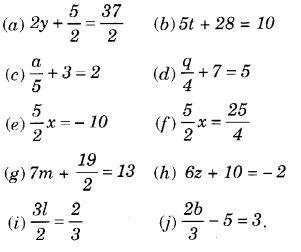

हल: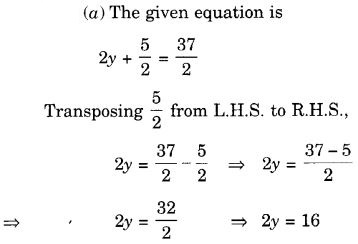

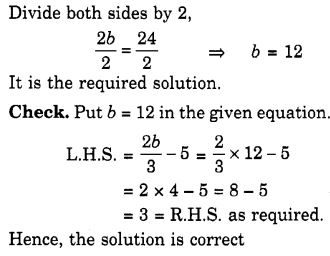
प्रश्न 2.
निम्नलिखित समीकरण हल करें:

(a) 2 (x + 4) = 12
(6) 3 (n – 5) = 21
(c) 3 (n – 5) = -21
(d) -4 (2 + x) = 8
(e) 4 (2 – x) = 8

समाधान:

प्रश्न 3.
निम्नलिखित समीकरणों को हल करें:

(a) 4 = 5 (p – 2)
(b) -4 = 5 (p – 2)
(c)  16 = 4 + 3 (t + 2)
(d)  4 + 5 (p – 1) = 34
(e) 0 = 16 + 4 (m – 6)

समाधान:

प्रश्न 4.
(a) x = 2 से शुरू करते हुए 3 समीकरण बनाइए
(b) x = – 2 से शुरू करते हुए 3 समीकरण बनाइए।
हल:
(a) 1. x = 2 से शुरू कीजिए
दोनों पक्षों को 3 से गुणा कीजिए, 3x = 6
दोनों पक्षों से 2 घटाइए, 3x – 2 = 4 …(1)

2. x = 2 से शुरू करें
दोनों पक्षों को 4 से गुणा करें, 4x = 8
दोनों पक्षों में 5 जोड़ें, 4x + 5 = 13 …(2)

3. x = 2 से शुरू करें दोनों पक्षों को 5 से गुणा करें 5x = 10
दोनों पक्षों से 1 घटाएं, 5x - 1 = 9 ...(3)

(b) पहला समीकरण:
x = -2 से शुरू करें
दोनों पक्षों को 2 से गुणा करें, 2x = -4
दोनों पक्षों से 3 घटाएँ, 2x – 3 = -7

दूसरा समीकरण:
x = – 2 से शुरू करें
दोनों पक्षों को – 5 से गुणा करें, – 5x = 10
दोनों पक्षों में 10 जोड़ें, 10 – 5x = 20

तीसरा समीकरण:
x = -2 से शुरू करें,
दोनों पक्षों को 2 से विभाजित करें,एक्स2= -1
दोनों पक्षों में 3 जोड़ें,एक्स2+ 3 = 2

Ex 4.4

प्रश्न 1.
निम्नलिखित स्थितियों में अज्ञात संख्याएँ ज्ञात करने के लिए समीकरण बनाइए और उन्हें हल कीजिए:

(a) किसी संख्या के आठ गुने में 4 जोड़ें; आपको 60 प्राप्त होता है।
(b) किसी संख्या का पाँचवाँ भाग घटाने पर 3 प्राप्त होता है।
(c) यदि मैं किसी संख्या का तीन-चौथाई भाग लेकर उसमें 3 जोड़ दूँ, तो मुझे 21 प्राप्त होता है।
(d) मैंने किसी संख्या के दोगुने में से 11 घटाया, परिणाम 15 प्राप्त हुआ।
(e) मुन्ना ने अपनी नोटबुक की संख्या का तिगुना 50 में से घटाया, तो उसे परिणाम 8 प्राप्त हुआ।
(f) इबेनहाल एक संख्या सोचती है। यदि वह इसमें 19 जोड़ दे और योग को 5 से भाग दे, तो उसे 8 प्राप्त होगा। (g) अनवर एक संख्या सोचता है। यदि वह उस संख्या के \(\frac { 5 }{ 2 } \) भाग में से 7 घटा दे, तो परिणाम 23 प्राप्त होता है।

52 of the number, the result is 23.

समाधान: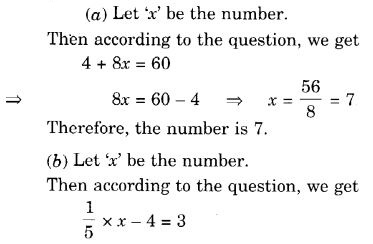

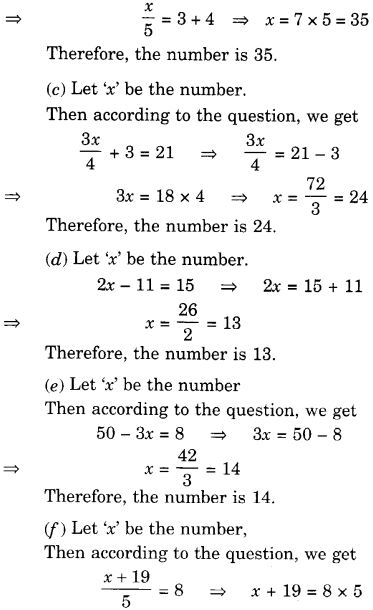
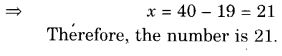
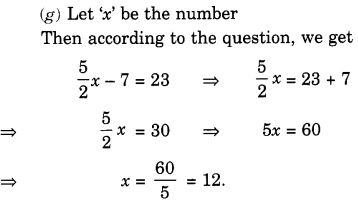
प्रश्न 2.
निम्नलिखित को हल करें:
(a) शिक्षिका ने कक्षा को बताया कि उसकी कक्षा में एक छात्र द्वारा प्राप्त अधिकतम अंक न्यूनतम अंक के दोगुने और 7 के योग के बराबर हैं। अधिकतम अंक 87 हैं। न्यूनतम अंक क्या है?
(b) एक समद्विबाहु त्रिभुज में, आधार कोण बराबर होते हैं। शीर्ष कोण 40° है। त्रिभुज के आधार कोण क्या हैं? (याद रखें, त्रिभुज के तीनों कोणों का योग 180° होता है)। 

(c) सचिन ने राहुल से दोगुने रन बनाए। कुल मिलाकर, उनके रन दोहरे शतक से दो रन कम थे। प्रत्येक ने कितने रन बनाए? 

हल:

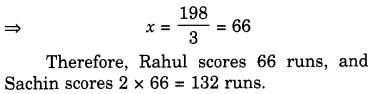
प्रश्न 3.
निम्नलिखित को हल करें:

1. इरफ़ान कहता है कि उसके पास 7 कंचे हैं जो परमीत के पास मौजूद कंचों के पाँच गुने से भी ज़्यादा हैं। इरफ़ान के पास 37 कंचे हैं। परमीत के पास कितने कंचे हैं?
2. लक्ष्मी के पिता 49 वर्ष के हैं। वह लक्ष्मी की आयु के तीन गुने से 4 वर्ष बड़े हैं। लक्ष्मी की आयु क्या है?
3. सुंदरग्राम के लोगों ने गाँव के बगीचे में पेड़ लगाए। कुछ पेड़ फलदार थे। गैर-फलदार पेड़ों की संख्या, फलदार पेड़ों की संख्या के तीन गुने से दो अधिक थी। यदि गैर-फलदार पेड़ों की संख्या 77 थी, तो लगाए गए फलदार पेड़ों की संख्या क्या थी?

समाधान:

प्रश्न 4.
निम्नलिखित पहेली को हल करें:
मैं एक संख्या हूँ, मुझे मेरी पहचान बताओ!
मुझे सात बार ले लो और एक पचास जोड़ो!
एक तिहरे शतक तक पहुंचने के लिए आपको अभी भी चालीस की जरूरत है!
समाधान:
'x' को संख्या मानें,
फिर, प्रश्न के अनुसार, हमें मिलता है (x × 7) + 50 = 300 - 40
7x + 50 = 260
7x = 210
x = \(\frac { 210 }{ 7 } \) = 30 तो, संख्या 30 है।2107 = 30