NCERT Class 7 Maths Chapter 6 त्रिभुज और उसके गुण

 NCERT Class 7 Maths Chapter 6 त्रिभुज और उसके गुण

NCERT Solutions for Class 7 Maths Chapter 6 त्रिभुज और उसके गुण

Ex 6.1

प्रश्न 1.
निम्नलिखित के लिए रफ रेखाचित्र बनाएं:

(a) ∆ ABC में, BE एक माध्यिका है।
(b) ∆ PQR में, PQ और PR त्रिभुज के शीर्षलंब हैं।
(c) ∆ XYZ में, YL त्रिभुज के बाह्य में एक शीर्षलंब है।

समाधान: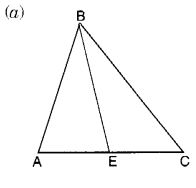

प्रश्न 2.
एक आरेख खींचकर सत्यापित कीजिए कि क्या एक समद्विबाहु त्रिभुज की माध्यिका और शीर्षलंब समान हो सकते हैं।
हल:
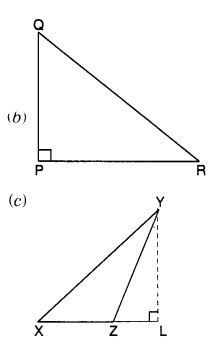
AD माध्यिका है।
AL शीर्षलंब है।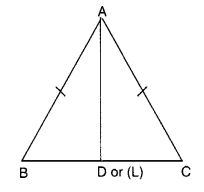

एक रेखाखंड BC खींचिए। कागज़ को मोड़कर BC का लंब समद्विभाजक ज्ञात कीजिए । मोड़ा हुआ मोड़ BC से उसके मध्य-बिंदु D पर मिलता है।
इस लंब समद्विभाजक पर कोई भी बिंदु A लीजिए। AB और AC को मिलाइए। इस प्रकार प्राप्त त्रिभुज एक समद्विबाहु ∆ABC है जिसमें AB = AC है।

चूँकि D, BC का मध्य-बिंदु है, इसलिए AD इसकी माध्यिका है। साथ ही, AD, BC का लंब समद्विभाजक है। अतः, AD, ∆ABC का शीर्षलंब है।
इस प्रकार, यह सत्यापित होता है कि एक समद्विबाहु त्रिभुज की माध्यिका और शीर्षलंब समान होते हैं।

Ex 6.2

प्रश्न 1.
निम्नलिखित आरेखों में अज्ञात बाह्य कोण x का मान ज्ञात कीजिए: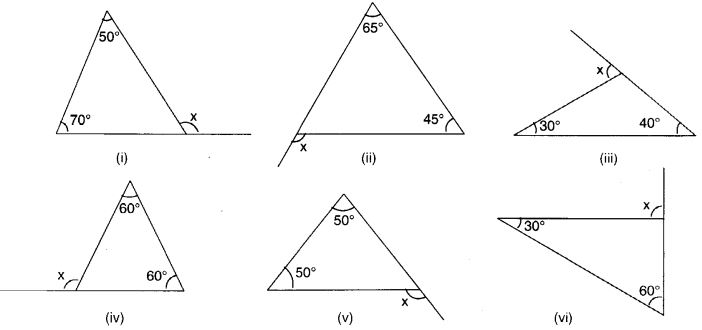

हल:

प्रश्न 2.
निम्नलिखित आकृतियों में अज्ञात आंतरिक कोण x का मान ज्ञात कीजिए: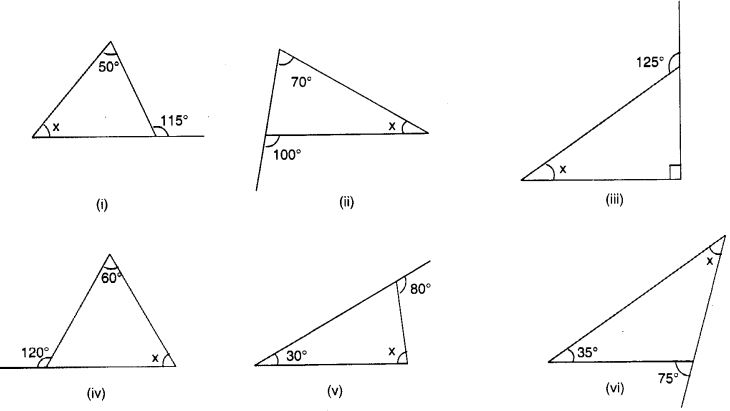

हल:

Ex 6.3

प्रश्न 1.
निम्नलिखित आरेखों में अज्ञात x का मान ज्ञात कीजिए: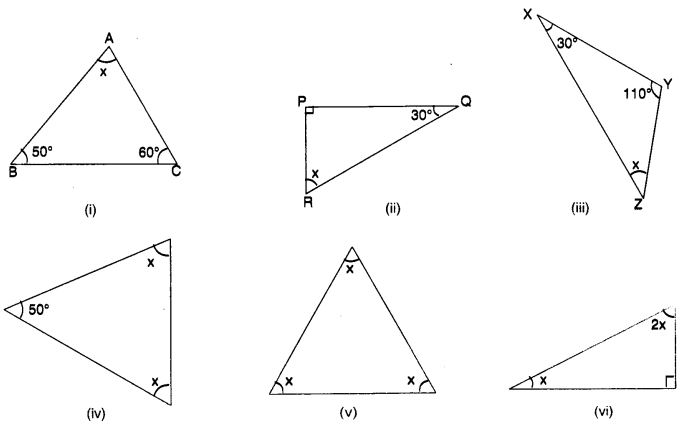

हल: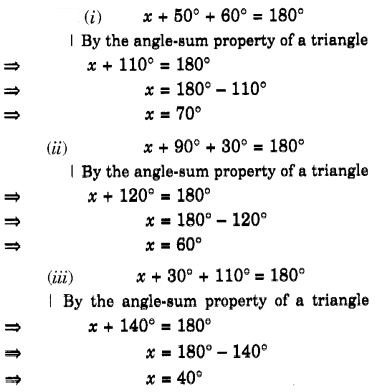

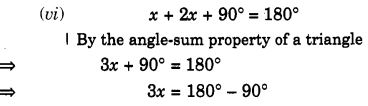
प्रश्न 2.
निम्नलिखित आरेखों में अज्ञात x और y के मान ज्ञात कीजिए: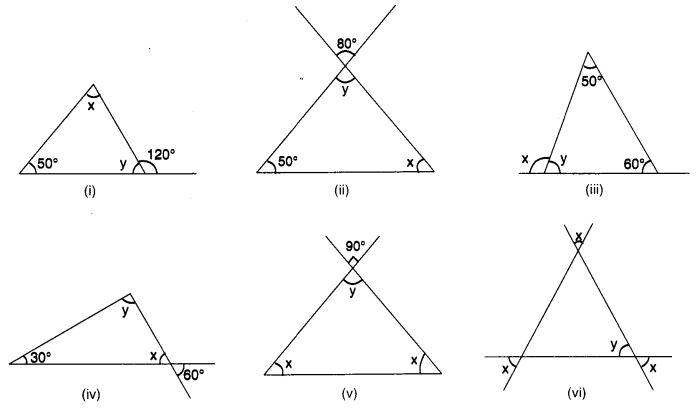

हल:

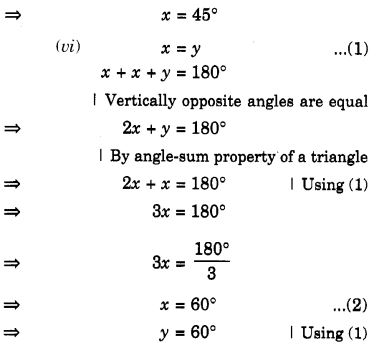
Ex 6.4

प्रश्न 1.
क्या निम्नलिखित भुजाओं वाला त्रिभुज संभव है?

1. 2 सेमी, 3 सेमी, 5 सेमी
2. 3 सेमी, 6 सेमी, 7 सेमी
3. 6 सेमी, 3 सेमी, 2 सेमी.

समाधान:

1. चूँकि, 2 + 3 > 5
   इसलिए दी गई भुजाओं की लम्बाई त्रिभुज नहीं बना सकती।
2. हमारे पास है, 3 + 6 > 7, 3 + 7 > 6 और 6 + 7 > 3
   यानी, किन्हीं दो भुजाओं का योग तीसरी भुजा से बड़ा है।
   इसलिए, ये भुजाएँ मिलकर एक त्रिभुज बनाती हैं।
3. हमारे पास है, 6 + 3 > 2, 3 + 2 Undefined control sequence \ngtr 6
   इसलिए, दी गई भुजा की लंबाई एक त्रिभुज नहीं बना सकती है।

प्रश्न 2.
त्रिभुज PQR के अभ्यंतर में कोई बिंदु O लीजिए।

1. ओपी + ओक्यू > पीक्यू ?
2. ओक्यू + ओआर > क्यूआर?
3. या + ओपी > आरपी ?

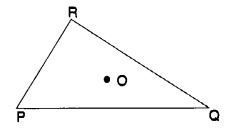
समाधान:

1. हाँ ! OP + OQ > PQ …(1)
   त्रिभुज की किन्हीं दो भुजाओं की लंबाइयों का योग तीसरी भुजा की लंबाई से अधिक होता है।
2. हाँ! OQ + OR > QR …(2)
   किसी त्रिभुज की किन्हीं दो भुजाओं की लंबाइयों का योग तीसरी भुजा की लंबाई से अधिक होता है।
3. हाँ! OR + OP > RP …(3)
   किसी त्रिभुज की किन्हीं दो भुजाओं की लंबाइयों का योग तीसरी भुजा की लंबाई से अधिक होता है।

प्रश्न 3.
त्रिभुज ABC की एक माध्यिका AM है। क्या AB + BC + CA > 2 AM है?
(त्रिभुज ∆ ABM और ∆ AMC की भुजाओं पर विचार कीजिए।)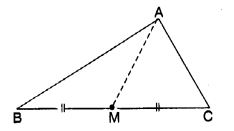

हल:
त्रिभुज ABM और AMC में त्रिभुज असमानता गुण का उपयोग करते हुए, हम पाते हैं कि
AB + BM > AM …(1) और, AC + MC > AM …(2)
दोनों ओर (1) और (2) जोड़ने पर, हम पाते हैं कि
AB + (BM + MC) + AC > AM + AM
⇒ AB + BC + AC > 2AM

प्रश्न 4.
ABCD एक चतुर्भुज है।
क्या AB + BC + CD + DA > AC + BD है?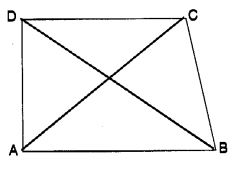

हल:
∆ ABC में, AB + BC > AC …(1)
त्रिभुज की किन्हीं दो भुजाओं की लंबाई का योग तीसरी भुजा की लंबाई से अधिक होता है
∆ ACD में, CD + DA > AC …(2)
त्रिभुज की किन्हीं दो भुजाओं की लंबाई का योग तीसरी भुजा की लंबाई से अधिक होता है
(1) और (2) को जोड़ने पर,
AB + BC + CD + DA > 2AC …(3)
∆ ABD में, AB + DA > BD …(4)
त्रिभुज की किन्हीं दो भुजाओं की लंबाई का योग तीसरी भुजा की लंबाई से अधिक होता है
∆ BCD में, BC + CD > BD …(5)
त्रिभुज की किन्हीं दो भुजाओं की लंबाई का योग तीसरी भुजा की लंबाई से अधिक होता है
(4) और (5) को जोड़ने पर,
AB + BC + CD + DA > 2BD …(6)
(3) और (6) को जोड़ने पर,
2 [AB + BC + CD + DA] > 2 (AC + BD)
⇒ AB + बीसी + सीडी + डीए > एसी + बीडी.

प्रश्न 5.
ABCD एक चतुर्भुज है। क्या AB + BC + CD + DA < 2 (AC + BD) है?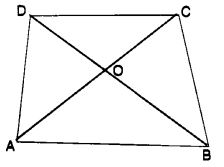

हल:
∆OAB में, OA + OB > AB ….(1)
त्रिभुज की किन्हीं दो भुजाओं की लंबाइयों का योग तीसरी भुजा की लंबाई से अधिक होता है।
∆OBC में, OB + OC > BC ….(2)
त्रिभुज की किन्हीं दो भुजाओं की लंबाइयों का योग तीसरी भुजा की लंबाई से अधिक होता है।
∆ OCA में,OC + OA > CA ….(3)
त्रिभुज की किसी भी दो भुजाओं की लंबाई का योग तीसरी भुजा की लंबाई से अधिक होता है
∆ OAD में, OA + OD > AD ….(4)
त्रिभुज की किसी भी दो भुजाओं की लंबाई का योग तीसरी भुजा की लंबाई से अधिक होता है
(1), (2), (3) और (4) को जोड़ने पर,
2(OA + OB + OC + OD) > AB + BC + CD + DA
⇒ AB + BC + CD + DA < 2 (OA + OB + OC + OD)
⇒ AB + BC + CD + DA < 2 (OA + OC + OB + OD)
⇒ AB + BC + CD + DA < 2 (AC + BD).

प्रश्न 6.
एक त्रिभुज की दो भुजाओं की लंबाई 12 सेमी और 15 सेमी है। तीसरी भुजा की लंबाई किन दो मापों के बीच होनी चाहिए?
हल:
मान लीजिए तीसरी भुजा की लंबाई x सेमी है।
∴ त्रिभुज की किन्हीं दो भुजाओं की लंबाइयों का योग तीसरी भुजा की लंबाई से अधिक होता है।
∴ हमें प्राप्त होना चाहिए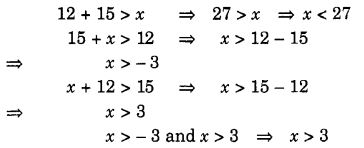

∴ तीसरी भुजा की लंबाई 3 सेमी और 27 सेमी के बीच कोई भी लंबाई होनी चाहिए।

Ex 6.5

प्रश्न 1.
PQR एक त्रिभुज है जिसका कोण P समकोण है। यदि PQ = 10 सेमी और PR = 24 सेमी है, तो QR ज्ञात कीजिए।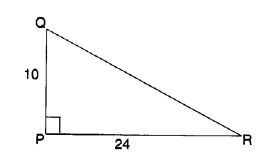

हल:
QR 2 = 10 2 + 24 2 पाइथागोरस गुणधर्म से
⇒ = 100 + 576 = 676
⇒ QR = 26 सेमी।

प्रश्न 2.
ABC एक त्रिभुज है जिसका कोण C समकोण है। यदि AB – 25 सेमी और AC = 7 सेमी है, तो BC ज्ञात कीजिए।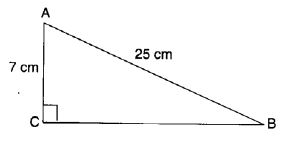

हल:
AC 2 + BC 2 = AB 2 पाइथागोरस गुणधर्म से
⇒ 7 2 + BC 2 = 25 2
⇒ 49 + BC 2 = 625
⇒ BC 2 = 625 – 49
⇒ BC 2 = 576
⇒ BC = 24 सेमी.

प्रश्न 3.
एक 15 मीटर लंबी सीढ़ी को a दूरी पर एक दीवार के सहारे रखने पर यह ज़मीन से 12 मीटर ऊँची एक खिड़की तक पहुँचती है। दीवार से सीढ़ी के पाद की दूरी ज्ञात कीजिए।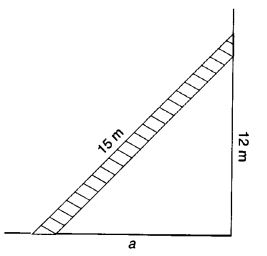

हल:
मान लीजिए दीवार से सीढ़ी के पाद की दूरी a मीटर है। अतः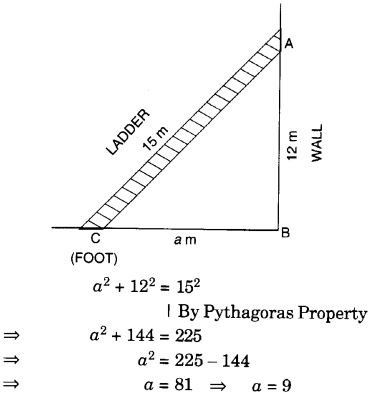

, दीवार से सीढ़ी के पाद की दूरी 9 मीटर है।

प्रश्न 4.
निम्नलिखित में से कौन सी भुजाएँ एक समकोण त्रिभुज की हो सकती हैं?

1. 2.5 सेमी, 6.5 सेमी, 6 सेमी.
2. 2 सेमी, 2 सेमी, 5 सेमी.
3. 1.5 सेमी, 2 सेमी, 2.5 सेमी.

समकोण त्रिभुजों के मामले में, समकोण पहचानें।
हल:
1. 2.5 सेमी, 6.5 सेमी, 6 सेमी हम देखते हैं कि
(2.5) 2 + 6 2 = 6.25 + 36 = 42.25 = (6.5) 2
इसलिए, दी गई लंबाइयाँ एक समकोण त्रिभुज की भुजाएँ हो सकती हैं। साथ ही, लंबाइयों, 2.5 सेमी और 6 सेमी के बीच का कोण भी एक समकोण है।

2. 2 सेमी, 2 सेमी, 5 सेमी
∵ 2 + 2 = 4Undefined control sequence \ngtr5
∴ दी गई लंबाई त्रिभुज की भुजाएँ नहीं हो सकतीं।
त्रिभुज की किन्हीं दो भुजाओं की लंबाइयों का योग तीसरी भुजा से अधिक होता है।

3. 1.5 सेमी, 2 सेमी, 2.5 सेमी हम पाते हैं कि
1.5 2 + 2 2 = 2.25 + 4 = 6.25 = 2.5 2
इसलिए, दी गई लंबाइयाँ एक समकोण त्रिभुज की भुजाएँ हो सकती हैं।
साथ ही, 1.5 सेमी और 2 सेमी लंबाइयों के बीच का कोण एक समकोण है।

प्रश्न 5.
एक पेड़ जमीन से 5 मीटर की ऊंचाई पर टूटा हुआ है और इसका शीर्ष पेड़ के आधार से 12 मीटर की दूरी पर जमीन को छूता है। पेड़ की मूल ऊंचाई ज्ञात कीजिए।
हल:
AC = CD दिया गया है
समकोण त्रिभुज DBC में, DC 2 = BC 2 + BD 2
पाइथागोरस गुण द्वारा = 5 2 + 12 2 = 25 + 144 = 169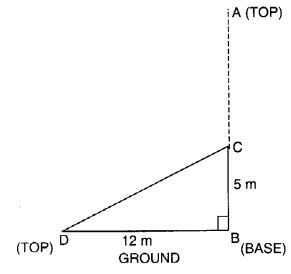

⇒ DC = 13 ⇒ AC = 13
⇒ AB = AC + BC = 13 + 5 = 18
इसलिए, पेड़ की मूल ऊंचाई = 18 मीटर।

प्रश्न 6.
एक ∆ PQR के कोण Q और R क्रमशः 25° और 65° हैं। निम्नलिखित में से कौन सा सत्य है? लिखिए: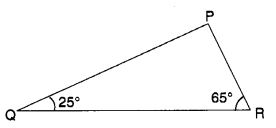

(i) PQ 2 + QR 2 = RP 2
(ii) PQ 2 + RP 2 = QR 2
(iii) RP 2 + QR 2 = PQ 2
हल:
(ii) PQ 2 + RP 2 = QR 2 सत्य है।

प्रश्न 7.
उस आयत का परिमाप ज्ञात कीजिए जिसकी लंबाई 40 सेमी और विकर्ण 41 सेमी है।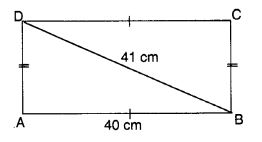

हल:
समकोण त्रिभुज DAB में, AB 2 + AD 2 = BD 2
⇒ 40 2 + AD 2 = 41 2 ⇒ AD 2 = 41 2 – 40 2
⇒ AD 2 = 1681 – 1600
⇒ AD 2 = 81 ⇒ AD = 9
∴ आयत का परिमाप = 2(AB + AD) = 2(40 + 9) = 2(49) = 98 सेमी
इसलिए, आयत का परिमाप 98 सेमी है।

प्रश्न 8.
एक समचतुर्भुज के विकर्ण 16 सेमी और 30 सेमी माप के हैं। इसका परिमाप ज्ञात कीजिए।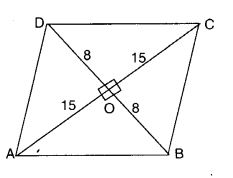

हल:
मान लीजिए ABCD एक समचतुर्भुज है जिसके विकर्ण BD और AC क्रमशः 16 सेमी और 30 सेमी लंबाई के हैं।
मान लीजिए विकर्ण BD और AC एक दूसरे को बिंदु O पर प्रतिच्छेद करते हैं
। चूँकि समचतुर्भुज के विकर्ण एक दूसरे को समकोण पर समद्विभाजित करते हैं। अतः
BO = OD = 8 सेमी,
AO = OC = 15 सेमी,
∠AOB = ∠BOC
= ∠COD = ∠DOA = 90°
समकोण त्रिभुज AOB में।
AB 2 = OA 2 + OB 2
पाइथागोरस गुण से
⇒ AB 2 = 15 2 + 8 2
⇒ AB 2 = 225 + 64
⇒ AB 2 = 289
⇒ AB = 17 सेमी
इसलिए, समचतुर्भुज ABCD का परिमाप = 4 भुजा = 4 AB = 4 × 17 सेमी = 68 सेमी
इसलिए, समचतुर्भुज का परिमाप 68 सेमी है।