SikhLo - Current Affairs in Hindi, Daily current affairs, Current affairs

 NCERT Class 7 Maths Chapter 7 त्रिभुजों की सर्वांगसमता

NCERT Solutions for Class 7 Maths Chapter 7 त्रिभुजों की सर्वांगसमता

Ex 7.1

प्रश्न 1.
निम्नलिखित कथनों को पूरा करें:
(a) दो रेखाखंड सर्वांगसम होते हैं यदि……..
(b) दो सर्वांगसम कोणों में से एक का माप 70° है; दूसरे कोण का माप……. ​​है।
(c) जब हम ∠A = ∠B लिखते हैं, तो हमारा वास्तव में मतलब होता है….
हल:
(a) उनकी लंबाई समान है
(b) 70°
(c) m∠A = m∠B

प्रश्न 2.
सर्वांगसम आकृतियों के कोई दो वास्तविक उदाहरण दीजिए।

1. एक ही मूल्यवर्ग के दो सिक्के या नोट।
2. एक ही ताले की दो चाबियाँ।

प्रश्न 3.
यदि ABC ↔ FED के अनुरूप ∆ ABC = ∆ FED है, तो त्रिभुजों के सभी संगत सर्वांगसम भाग लिखिए।
हल:
संगत शीर्ष: A और F; B और E; C और D.
संगत भुजाएँ: \(\overline { AB } \) और \(\overline { FE } \) ; \(\overline { BC } \) और \(\overline { ED } \); \(\overline { CA } \) और \(\overline { DF } \). संगत कोण: ∠A और ∠F; ∠B और ∠E; ∠C और ∠D.AB¯¯¯¯¯¯¯¯ and FE¯¯¯¯¯¯¯¯ ; BC¯¯¯¯¯¯¯¯ and ED¯¯¯¯¯¯¯¯; CA¯¯¯¯¯¯¯¯ and DF¯¯¯¯¯¯¯¯.

प्रश्न 4.
यदि ∆ DEF = ∆ BCA, तो ∆ BCA का वह भाग लिखिए जो किसके संगत है?

1. ∠E
2. EF¯¯¯¯¯¯¯¯
3. ∠F
4. DF¯¯¯¯¯¯¯¯

समाधान:

1. ∠सी
2. CA¯¯¯¯¯¯¯¯
3. ∠A
4. BA¯¯¯¯¯¯¯¯

Ex 7.2

प्रश्न 1.
निम्नलिखित में आप किस सर्वांगसमता मानदंड का उपयोग करते हैं?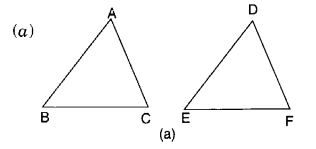

दिया गया है:
अतः
AC = DF
AB = DE
BC = EF
अतः ∆ ABC = ∆ DEF

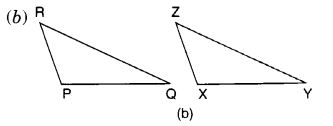
दिया गया है: ZX = RP
RQ = ZY
∠PRQ = ∠XZY
अतः, ∆ PQR ≅ ∆ XYZ

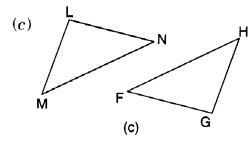
दिया गया है: ∠MLN = ∠ FGH
∠NML = ∠GFH
ML = GF
अतः, ∆ LMN ≅ ∆ GFH

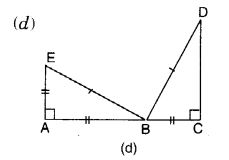
दिया गया है: EB = DB
AE = BC
∠A = ∠C = 90°
अतः, ∆ ABE ≅ ∆ CDB
हल:

(a) एसएसएस सर्वांगसमता मानदंड
(b) एसएएस सर्वांगसमता मानदंड
(c) एएसए सर्वांगसमता मानदंड
(d) आरएचएस सर्वांगसमता मानदंड।

प्रश्न 2.
आप दर्शाना चाहते हैं कि ∆ ART ≅ ∆ PEN,

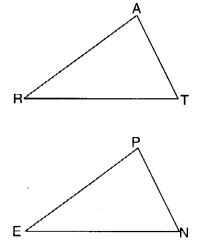
(a) यदि आपको एसएसएस मानदंड का उपयोग करना है, तो आपको दिखाना होगा
(i)एआर = (ii)आरटी = (iii)एटी =

(b)
यदि यह दिया गया है कि ∠T = ∠N और आपको SAS मानदंड का उपयोग करना है, तो आपको (i) RT = और (ii) PN = की आवश्यकता है

(c) यदि यह दिया गया है कि AT = PN और आपको ASA मानदंड का उपयोग करना है, तो आपको
(i) ? (ii) ?
हल की आवश्यकता है:

प्रश्न 3.
आपको दर्शाना है कि ∆ AMP = ∆ AMQ है।
निम्नलिखित प्रमाण में, लुप्त कारण बताइए।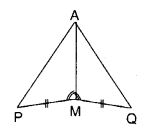


हल:

प्रश्न 4.
∆ ABC में, ∠A = 30°, ∠B = 40° और ∠C = 110°
∆ PQR में, ∠P = 30°, ∠Q = 40° और ∠R = 110°
एक छात्र कहता है कि ∆ ABC = ∆ PQR? AAA सर्वांगसमता मानदंड से। क्या वह उचित है? क्यों या क्यों नहीं?
हल:
नहीं! वह उचित नहीं है क्योंकि AAA त्रिभुजों की सर्वांगसमता के लिए मानदंड नहीं है।

प्रश्न 5.
आकृति में, दो त्रिभुज सर्वांगसम हैं। संगत भाग चिह्नित हैं। हम लिख सकते हैं ∆ RAT = ?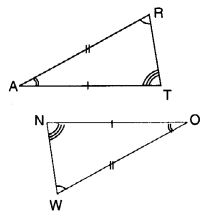

हल:
∆ RAT ≅ ∆ WON

प्रश्न 6.
सर्वांगसमता कथन को पूरा करें: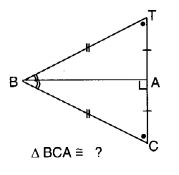


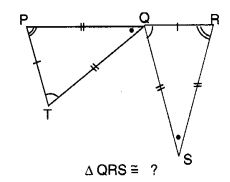
हल:
∆ BCA = ∆ BTA
∆ QRS = ∆ TPQ

प्रश्न 7.
एक वर्गाकार शीट पर, बराबर क्षेत्रफल वाले दो त्रिभुज इस प्रकार बनाएं कि

1. त्रिभुज सर्वांगसम हैं
2. त्रिभुज सर्वांगसम नहीं हैं। आप उनके परिमापों के बारे में क्या कह सकते हैं?

समाधान:

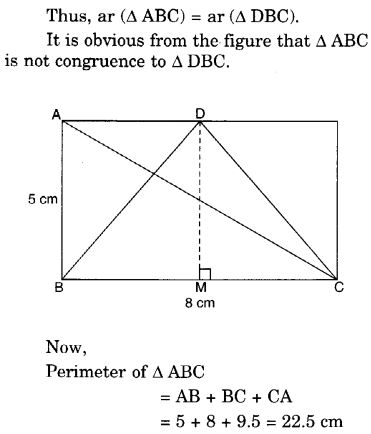
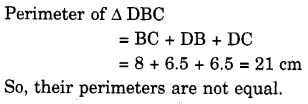
प्रश्न 8.
दो त्रिभुजों का एक रफ चित्र इस प्रकार खींचिए कि उनके सर्वांगसम भागों के पाँच युग्म हों, लेकिन फिर भी त्रिभुज सर्वांगसम न हों।
हल: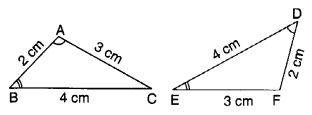

∆ ABC और ∆ DEF में,
AB = DF (= 2 सेमी)
BC = ED (= 4 सेमी)
CA = EF (= 3 सेमी)
∠BAC = ∠EDF
∠ABC = ∠DEF
लेकिन ∆ ABC, ∆ DEF के सर्वांगसम नहीं है।

प्रश्न 9.
यदि ∆ ABC और ∆ PQR सर्वांगसम हों, तो संगत भागों का एक अतिरिक्त युग्म लिखिए। आपने किस मानदंड का प्रयोग किया?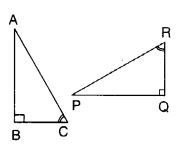

हल:
ASA सर्वांगसमता नियम से BC = RQ।

प्रश्न 10.
व्याख्या कीजिए कि क्यों ∆ ABC ≅ ∆ FED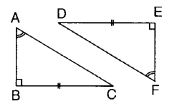

हल:
∠ABC = ∠FED (= 90°) BC = ED
∠ACB = ∠FDE
∵ एक त्रिभुज के तीनों कोणों के मापों का योग 180° होता है।
∆ ABC ≅ ∆ FED (SAS सर्वांगसमता मानदंड से)