NCERT Class 7 Maths Chapter 1 पूर्णांक
NCERT Solutions for Class 7 Maths Chapter 1 पूर्णांक
Ex 1.1
निम्नलिखित संख्या रेखा किसी विशेष दिन विभिन्न स्थानों पर डिग्री सेल्सियस (°C) में तापमान दर्शाती है।

(a) इस संख्या रेखा का अवलोकन कीजिए और इस पर अंकित स्थानों का तापमान लिखिए।
(b) उपरोक्त में से सबसे गर्म और सबसे ठंडे स्थानों के बीच तापमान का अंतर क्या है?
(c) लाहुलस्पीति और श्रीनगर के बीच तापमान का अंतर क्या है?
(d) क्या हम कह सकते हैं कि श्रीनगर और शिमला का कुल तापमान शिमला के तापमान से कम है? क्या यह श्रीनगर के तापमान से भी कम है?
उत्तर:
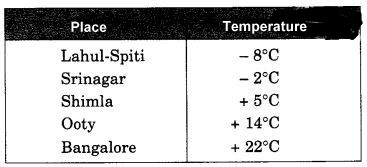
(b) सबसे गर्म और सबसे ठंडे स्थानों के बीच तापमान का अंतर
= बेंगलुरु का तापमान - लाहुलस्पीति का तापमान
= 22°C - (- 8°C) = 22°C + 8°C
= 30°C
(c) लाहुलस्पीति और श्रीनगर के बीच तापमान का अंतर
= श्रीनगर का तापमान - लाहुलस्पीति का तापमान
= - 2°C - (- 8°C) = - 2°C + 8°C = 6°C
(d) श्रीनगर और शिमला का तापमान
= श्रीनगर का तापमान + शिमला का तापमान
= - 2°C + 5°C = 3°C
3°C < 5°C
हाँ, श्रीनगर और शिमला के तापमान का योग शिमला के तापमान से कम है। अब, श्रीनगर का तापमान = - 2°C
साथ ही 3°C > - 2°C
नहीं, श्रीनगर और शिमला के तापमान का योग श्रीनगर के तापमान से कम नहीं है।
प्रश्न 2.
एक प्रश्नोत्तरी में, सही उत्तरों के लिए धनात्मक अंक और गलत उत्तरों के लिए ऋणात्मक अंक दिए जाते हैं। यदि जैक के पाँच क्रमागत राउंड में अंक 25, -5, -10, 15 और 10 थे, तो अंत में उसके कुल अंक क्या थे?
उत्तर:
पहले राउंड में अंक = 25
दूसरे राउंड में अंक = -5
तीसरे राउंड में अंक = -10 चौथे
राउंड में अंक = 15 पाँचवें
राउंड में अंक = 10
अंत में कुल अंक
= 25 + (-5) + (-10) + 15 + 10
= 25 – 5 – 10 + 15 + 10
= 25 + 15 + 10 – 5 – 10
= 50 – 15 = 35
प्रश्न 3.
श्रीनगर में सोमवार को तापमान -5°C था और फिर मंगलवार को इसमें 2°C की गिरावट आई। मंगलवार को श्रीनगर का तापमान कितना था? बुधवार को इसमें 4°C की वृद्धि हुई। इस दिन तापमान कितना था?
उत्तर:
सोमवार को श्रीनगर का तापमान = -5°C
मंगलवार को श्रीनगर के तापमान में गिरावट = 2°C
∴ मंगलवार को श्रीनगर का तापमान = -5°C - 2°C = -7°C
बुधवार को श्रीनगर के तापमान में वृद्धि = 4°C
∴ बुधवार को श्रीनगर का तापमान = -7°C + 4°C = -3°C
प्रश्न 4.
एक हवाई जहाज़ समुद्र तल से 5000 मीटर की ऊँचाई पर उड़ रहा है। एक विशेष बिंदु पर, यह समुद्र तल से 1200 मीटर नीचे तैर रही एक पनडुब्बी के ठीक ऊपर है। उनके बीच ऊर्ध्वाधर दूरी क्या है?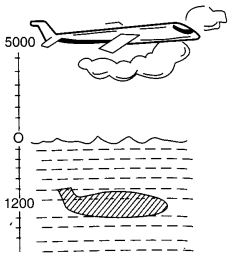
उत्तर:
चूँकि समुद्र तल 0 मीटर है और हवाई जहाज़ समुद्र तल से 5000 मीटर ऊपर है। साथ ही पनडुब्बी भी समुद्र तल से 1200 मीटर नीचे है, इसलिए हवाई जहाज़ और पनडुब्बी के बीच ऊर्ध्वाधर दूरी
= 5000 मीटर - (- 1200 मीटर)
= 5000 मीटर + 1200 मीटर
= 6200 मीटर है।
प्रश्न 5.
मोहन अपने बैंक खाते में ₹2,000 जमा करता है और अगले दिन उसमें से ₹1,642 निकाल लेता है। यदि खाते से राशि की निकासी को ऋणात्मक पूर्णांक द्वारा दर्शाया जाता है, तो आप जमा की गई राशि को कैसे दर्शाएँगे? निकासी के बाद मोहन के खाते में शेष राशि ज्ञात कीजिए।
उत्तर:
जमा राशि = ₹2000
निकाली गई राशि = ₹1642
मोहन के खाते में शेष = ₹2000 -
निकासी के बाद ₹1642 = ₹358
जमा की गई राशि को धनात्मक पूर्णांक द्वारा दर्शाया गया है।
प्रश्न 6.
रीता बिंदु A से बिंदु B तक 20 किमी पूर्व की ओर जाती है। B से वह उसी सड़क पर पश्चिम की ओर 30 किमी चलती है। यदि पूर्व की ओर की दूरी को एक धनात्मक पूर्णांक द्वारा दर्शाया जाता है, तो आप पश्चिम की ओर तय की गई दूरी को कैसे दर्शाएंगे? आप A से उसकी अंतिम स्थिति को किस पूर्णांक से दर्शाएंगे?
उत्तर:
पश्चिम की ओर की दूरी को ऋणात्मक पूर्णांक द्वारा दर्शाया गया है।
पूर्व और पश्चिम दिशाएँ एक दूसरे के विपरीत हैं।
पश्चिम की ओर तय की गई दूरी = - 30 किमी।
पूर्व की ओर तय की गई दूरी = + 20 किमी।
A से उसकी अंतिम स्थिति = + 20 किमी + (- 30 किमी) = 20 किमी - 30 किमी
= - 10 किमी
प्रश्न 7.
एक जादुई वर्ग में प्रत्येक पंक्ति, स्तंभ और विकर्ण का योग समान होता है। जाँच कीजिए कि निम्नलिखित में से कौन सा जादुई वर्ग है?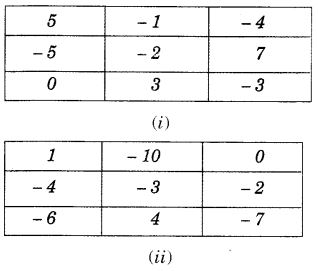
उत्तर:
I. पंक्ति , योग = 5 + (- 1) + (- 4)
= 5 + (- 5) = 0
II. पंक्ति, योग = (- 5) + (- 2) + 7
= (- 7) + 7 = 0
III. पंक्ति, योग = 0 + 3 + (- 3)
= 0 + 0 = 0
I. स्तंभ, योग = 5 + (- 5) + 0
= 0 + 0 = 0
II. स्तंभ, योग = (- 1) + (- 2) + 3
= (- 3) + 3 = 0
III. स्तंभ, योग = (- 4) + 7 + (- 3)
= 7 + (- 4) + (- 3)
= 7 + (- 7) = 0
एक विकर्ण, योग = 5 + (- 2) + (- 3) = 5 + (- 5) = 0
अन्य विकर्ण, योग = 0 + (- 2) + (- 4) = 0 + (- 6) = -6 ≠ 0
इसलिए, दिया गया वर्ग एक जादुई वर्ग नहीं है।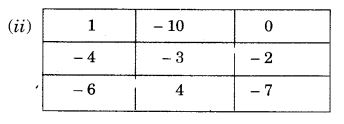
I. पंक्ति, योग = 1 + (- 10) + 0 = - 9
II. पंक्ति, योग = (- 4) + (- 3) + (- 2) = - 9
III. पंक्ति, योग = (- 6) + 4 + (- 7)
= 4 + (- 6) + (- 7)
= 4 + (- 13)
= – (13-4) = -9
I. स्तंभ, योग = 1 + (- 4) + (- 6)
= 1 + (- 10)
= -(10 – 1) = – 9
II. स्तंभ, योग = (- 10) + (- 3) + 4
= (-13)+ 4
= – (13-4) = -9
III. स्तंभ, योग = 0 + (- 2) + (- 7)
= 0 + (- 9) = – 9
एक विकर्ण, योग = 1 + (- 3) + (- 7)
= 1 + (- 10)
= -(10-1) = -9
अन्य विकर्ण, योग = (- 6) + (- 3) + 0
= (- 9) + 0 = – 9
चूंकि प्रत्येक पंक्ति, स्तंभ और विकर्ण का योग समान है, इसलिए, दिया गया वर्ग एक जादुई वर्ग है।
प्रश्न 8.
a और b के निम्नलिखित मानों के लिए a – (- b) = a + b सत्यापित करें।
(i) a = 21, b = 18
(ii) a = 118, b = 125.
(iii) a = 75, b = 84
(iv) a = 28, b = 11
उत्तर:
(i) बायाँ पक्ष = a – (-b) = 21 – (-18)
= 21 + 18 = 39
दायाँ पक्ष = a + b = 21 + 18 = 39
∴ a – (- b) = a + b
(ii) बायाँ पक्ष = a – (- b) = 118 – (-125)
= 118 + 125 = 243
दायाँ पक्ष = a + b = 118 + 125 = 243
∴ a – (- b) = a + b
(iii) बायाँ पक्ष = a – (- b) = 75 – (- 84)
= 75 + 84 = 159
दायाँ पक्ष = a + b = 75 + 84 = 159
∴ a – (-b) = a + b
(iv) बायाँ पक्ष = a – (- b) = 28 – (- 11)
= 28 + 11 = 39
दायाँ पक्ष = a + b = 28 + 11 = 39
∴ a – (- b) = a + b
प्रश्न 9.
कथनों को सत्य बनाने के लिए बॉक्स में >, < या = चिह्न का प्रयोग करें।
(a) (- 8) + (-4) …… (- 8) – (- 4)
(b) (-3) +7 – (19) …… 15-8 +(-9)
(c) 23 – 41 + 11 …… 23-41- 11
(d) 39 + (-24) – (15) …… 36+ (-52) – (- 36)
(e) – 231 + 79 + 51 …… -399 + 159 + 81.
हल:
(a) बायां पक्ष = (- 8) + (- 4)
= – (8 + 4) = – 12
दायां पक्ष = (- 8) – (- 4)
= – 8 + 4 = – (8 – 4) = – 4
∴ (-8) + (-4) < (-8)-(-4)
(b) बायां पक्ष = (-3) + 7 – (19)
= + 4 – (19)
= + 4 – 19
= -15
दायां पक्ष = 15 – 8 + (- 9)
= 7 + (-9) = 7- 9 = -2
∴ (- 3) + 7 – (19) < 15 – 8 + (- 9)
(c) बायां पक्ष = 23 – 41 + 11
= 23 + 11- 41
= 34 – 41 = – (41 – 34)
= – 7
दायां पक्ष = 23 – 41 – 11
= 23 – (41 + 11)
= 23 – 52
= – (52 – 23)
= – 29
∴ 23 – 41 + > 23 – 41 – 11
(d) बायां पक्ष = 39 + (- 24) – (15)
= 39 – 24 – (15)
= 15 – (15) = 0
दायां पक्ष = 36 + (- 52) – (- 36)
= – (52 – 36) – (- 36)
= – 16 – (- 36)
= – 16 + 36 = 20
∴ 39 + (- 24) – (15) < 36 + (- 52) – (- 36)
(e) बायां पक्ष = – 231 + 79 + 51
= – 231 + 130
= – (231 – 130) = – 101
दायां पक्ष = – 399 + 159 + 81
= – 399 + 240
= – (399 – 240)
= – 159
∴ – 231 + 79 + 51 > – 399 + 159 + 81.
प्रश्न 10.
एक पानी की टंकी के अंदर सीढ़ियाँ हैं। एक बंदर सबसे ऊपरी सीढ़ी (अर्थात पहली सीढ़ी) पर बैठा है। पानी का स्तर नौवीं सीढ़ी पर है।
(i) वह 3 सीढ़ियाँ नीचे कूदता है और फिर 2 सीढ़ियाँ ऊपर कूदता है। कितनी छलांगों में वह पानी के स्तर तक पहुँच जाएगा?
(ii) पानी पीने के बाद, वह वापस जाना चाहता है। इसके लिए, वह प्रत्येक चाल में 4 सीढ़ियाँ ऊपर कूदता है और फिर 2 सीढ़ियाँ नीचे कूदता है। कितनी छलांगों में वह सबसे ऊपर वाली सीढ़ी पर वापस पहुँच जाएगा?
(iii) यदि नीचे चली गई सीढ़ियों की संख्या को ऋणात्मक पूर्णांकों द्वारा और ऊपर चली गई सीढ़ियों की संख्या को धनात्मक पूर्णांकों द्वारा दर्शाया गया है, तो निम्नलिखित 1 को पूरा करके भाग (i) और (ii) में उसकी चालों को दर्शाइए:
(a) – 3 + 2 -… = – 8
(b) 4 – 2 + … = 8.
(a) में योग (- 8) आठ सीढ़ियाँ नीचे जाने को दर्शाता है। तो, (b) में योग 8 क्या दर्शाएगा?
उत्तर:
(i) जल स्तर तक पहुँचने के लिए उसकी छलांगें इस प्रकार होंगी:
(- 3) + 2 + (- 3) + 2 + (- 3) + 2 + (- 3) + 2 + (- 3) + 2 + (- 3) = - 8
इसलिए, 11 छलांगों में वह 1 नौवें चरण (जल स्तर) तक पहुँच जाएगा
(ii) शीर्ष चरण पर वापस पहुँचने के लिए उसकी छलांगें इस प्रकार होंगी:
4 + (-2) + 4 + (-2) + 4 = 8
इसलिए, वह 5 छलांगों में शीर्ष चरण पर वापस पहुँच जाएगा।
(iii) (a) (- 3) + 2 + (- 3) + 2 + (- 3) + 2 + (- 3 + 2) + (- 3) = - 8
(b)4 - 2 + 4 - 2 + 4 - 2 + 4 - 2 = 8
साथ ही (a) में योग (- 8) 8 सीढ़ियाँ नीचे जाने को दर्शाता है और (b) में योग (+ 8) 8 सीढ़ियाँ ऊपर जाने को दर्शाता है।
या
(i) बंदर की स्थिति:
(a) पहली छलांग चौथी सीढ़ी पर है।
(b) दूसरी छलांग दूसरी सीढ़ी पर है।
(c) तीसरी छलांग पाँचवीं सीढ़ी पर है।
(d) चौथी छलांग तीसरी सीढ़ी पर है।
(e) पाँचवीं छलांग छठी सीढ़ी पर है।
(f) छठी छलांग चौथी सीढ़ी पर है।
(g) सातवीं छलांग सातवीं सीढ़ी पर है।
(h) 8वीं छलांग 5वीं सीढ़ी पर है।
(i) 9वीं छलांग 8वीं सीढ़ी पर है।
(j) 10वीं छलांग 6वीं सीढ़ी पर है।
(k) 11वीं छलांग 9वीं सीढ़ी पर है।
∴ अभीष्ट छलांगों की संख्या = 11.
Ex 1.2
पूर्णांकों का एक युग्म लिखिए जिनका:
(a) योगफल - 7 है
(b) अंतर - 10 है
(c) योगफल 0 है
उत्तर:
(a) - 15 और 8
योगफल = - 15 + 8 = - 7
(b) – 30 और – 20
अंतर = – 30 – (- 20)
= -30 + 20 = – 10
(c) – 12 और + 12
अंतर = – 12 + (12)
= -12 + 12 = 0
प्रश्न 2.
(a) ऋणात्मक पूर्णांकों का एक युग्म लिखिए जिनका अंतर 8 हो।
(b) एक ऋणात्मक पूर्णांक और एक धनात्मक पूर्णांक लिखिए जिनका योग - 5 हो।
(c) एक ऋणात्मक पूर्णांक और एक धनात्मक पूर्णांक लिखिए जिनका अंतर - 3 हो।
उत्तर:
(a) - 13 और - 21
अंतर = -13 - (- 21)
= - 13 + 21 = 8
(b) – 15 और 10 का
योग = – 15 + 10 = – 5
(c) – 1 और 2
अंतर = – 1 – (+ 2)
= – 1 – 2 = – 3
प्रश्न 3.
एक प्रश्नोत्तरी में, टीम A ने तीन क्रमिक राउंड में - 40, 10, 0 और टीम B ने 10, 0, - 40 अंक प्राप्त किए। किस टीम ने अधिक अंक प्राप्त किए? क्या हम कह सकते हैं कि हम पूर्णांकों को किसी भी क्रम में जोड़ सकते हैं?
उत्तर:
टीम A के कुल अंक = (- 40) + 10 + 0
= - 40 + 10 + 0 = - 30
टीम B के कुल अंक = 10 + 0 + (- 40)
= 10 + 0 - 40 = 10 - 40 = - 30
अतः, दोनों टीमों के अंक बराबर थे। हाँ, हम कह सकते हैं कि हम पूर्णांकों को किसी भी क्रम में जोड़ सकते हैं।
प्रश्न 4.
निम्नलिखित कथनों को सत्य बनाने के लिए रिक्त स्थान भरें:
(i) (- 5) + (- 8) = (- 8) + (………………)
(ii) – 53 + …………… = – 53
(iii) 17 + ……………… = 0
(iv) [13 + (- 12)] + (…………..) = 13 + [(- 12) + (- 7)]
(v) (- 4) + [15 + (- 3)] = [- 4 + 15] + …………….
उत्तर:
(i) (- 5) + (- 8) = (- 8) + (- 5)
(ii) – 53 + 0 = – 53
(iii) 17 + (- 17) = 0
(iv) [13 + (- 12)] + (- 7) = 13 + [(-12) + (- 7)]
(v) (-4)+ [15 +(-3)] = [-4 + 15] + (- 3)
Ex 1.3
निम्नलिखित में से प्रत्येक गुणनफल ज्ञात कीजिए:
(a) 3 × (-1)
(b) (-1) × 225
(c) (-21) × (-30)
(d) (-316) × (-1)
(e) (-15) × 0 × (-18)
(f) (-12) × (-11) × (10)
(g) 9 × (-3) × (- 6)
(h) (-18) × (-5) × (-4)
(i) (-1) × (- 2) × (-3) × 4
(j) (-3) × (-6) × (-2) × (-1)
उत्तर:
(a) 3 × (-1) = – (3 × 1) = -3
(b) (-1) × 225 = – (1 × 225) = -225
(c) (-21) × (- 30) = 21 × 30 = 630
(d) (-316) × (-1) = 316 × 1 = 316
(e) (-15) × 0 × (-18) = (15 × 0) × 18
= 0 × 18 = 0
(f) (-12) × (-11) × 10
= [(-12) × (-11)] × 10
= (12 × 11) × 10 = 132 × 10 = 1320
(g) 9 × (-3) × (-6) = 9 × [(-3) × (-6)]
= 9 × (3 × 6) = 9 × 18 = 162
(h) (-18) × (-5) × (-4)
= [(-18) × (-5)] × (-4)
= (18 × 5) × (-4) = 90 × (-4)
= – (90 × 4) = -360
(i) (-1) × (-2) × (-3) × 4
= [(-1) × (-2)] × [(-3) × 4]
= (1 × 2) × [- (3 × 4)]
= 2 × [12] = 2 × (-12) = -24
(j) (-3) × (-6) × (-2) × (-1)
= [(-3) × (-6)] × [(- 2) × (-1)]
= (3 × 6) × (2 × 1) = 18 × 2 = 36
प्रश्न 2.
निम्नलिखित को सत्यापित करें:
(a) 18 × [7 + (-3)] = [18 × 7] + [18 × (-3)]
(b) (-21) × [(- 4) + (-6)]
= [(-21) × (- 4)] + [(-21) × (-6)]
उत्तर:
(a) बायाँ पक्ष = 18 × [7 + (-3)]
= 18 × [7-3] = 18 × 4 = 72 दायाँ पक्ष
= [18 × 7] + [18 × (-3)] = 126 + ( -54)
= 126 – 54 = 72
(b) बायाँ पक्ष = (-21) × [(-4) + (-6)]
= (-21) × [-4 -6]
= (-21) × (-10) = 210
दायाँ पक्ष = [(-21) × (-4)] + [(-21) × (-6)]
= (21 × 4) + (21 × 6)
= 84 + 126 = 210
∴ बायाँ पक्ष = दायाँ पक्ष
प्रश्न 3.
(i) किसी भी पूर्णांक a के लिए, (- 1) × a किसके बराबर है?
(ii) वह पूर्णांक ज्ञात कीजिए जिसका (-1) से गुणनफल है:
(a) -22
(b) 37
(c) 0
उत्तर:
(i) (-1) × a = – a
∴ (- 1) × (कोई भी पूर्णांक)
= पूर्णांक का योज्य व्युत्क्रम
(ii) (a) - 22 = (-1) × 22
(b) 37 = (-1) × (- 37)
(c) 0 = (-1) × 0
प्रश्न 4.
(-1) × 5 से शुरू करते हुए, (-1) × (-1) = 1
दिखाने के लिए कुछ पैटर्न दिखाते हुए विभिन्न गुणनफल लिखें।
उत्तर:
(-1) × 5 = -5 (-1) × 4 = -4 (-1) × 3 = -3 (-1) × 2 = -2 (-1) × 1 = -1 (-1) × 0 = 0 (-1) × (-1) = 1
उपयुक्त गुणों का उपयोग करके गुणनफल ज्ञात कीजिए:
(a) 26 × (-48) + (-48) × (-36)
(b) 8 × 53 × (-125)
(c) 15 × (-25) × (-4) × (-10)
(d) (-41) × 102
(e) 625 × (-35) + (-625) × 65
(f) 7 × (50 – 2)
(g) (-17) × (-29)
(h) (-57) × (-19) + 57
उत्तर:
(a) 26 × (- 48) + (-48) × (-36)
= (-48) × [26 + (-36)]
(वितरण गुण का उपयोग करके)
= (-48) × (26 – 36)
= (-48) × (-10) = 480
(b) 8 × 53 × (-125) = (8 × 53) × (-125)
(सहयोगी गुण का उपयोग करके)
= 424 × (-125) = -424 × 125 = – 53000
(c) 15 × (-25) × (-4) × (-10)
= [(-25) × (- 4)] × [(-10) × 15]
(सहचर्य गुण का उपयोग करके)
= (100) × (-150) = -100 × 150 = -15000
(d) (-41) × 102 = -(41 × 102)
= – [41 × (100 + 2)]
(वितरण गुण)
= – [41 × 100 + 41 × 2]
= – [4100 + 82] = -4182
(e) 625 × (-35) + (-625) × 65
= 625 × [-35 + (-1) (65)]
(वितरण गुण)
= 625 × [-35 -65]
= 625 × (-100) = -62500
(f) 7 × (50 – 2) = 7 × 50 + 7 × (-2)
= 350 – 14 = 336
(वितरण गुण का उपयोग करके)
(g) (-17) × (-29) = 17 × 29 = 17 × (30 – 1)
(वितरण गुण का उपयोग करके)
= 17 × 30 + 17 × (-1) = 510 – 17 = 493
(h) (-57) × (-19) + 57 = 57 × 19 + 57
= 57 × (19 + 1)
(वितरण गुण का उपयोग करके)
= 57 × 20 = 1140
प्रश्न 6.
एक निश्चित हिमीकरण प्रक्रिया के लिए कमरे के तापमान को 40°C से 5°C प्रति घंटे की दर से कम करना आवश्यक है। प्रक्रिया शुरू होने के 10 घंटे बाद कमरे का तापमान क्या होगा?
उत्तर:
कमरे का तापमान = 40°C
तापमान में परिवर्तन = - 5°C 10 घंटे में,
तापमान में परिवर्तन = 40°C + 10 x (-5)°C
= 40°C + (-50°C) = 40°C - 50°C = -10°C
प्रश्न 7.
10 प्रश्नों वाली एक कक्षा परीक्षा में प्रत्येक सही उत्तर के लिए 5 अंक और प्रत्येक गलत उत्तर के लिए (- 2) अंक और प्रयास न किए गए प्रश्नों के लिए 0 अंक दिए जाते हैं।
(i) मोहन को चार सही और छह गलत उत्तर मिलते हैं। उसके अंक क्या हैं?
(ii) रेशमा को पाँच सही उत्तर और पाँच गलत उत्तर मिलते हैं, उसके अंक क्या हैं?
(iii) हीना ने सात प्रश्नों में से दो सही और पाँच गलत उत्तर दिए। उसके अंक क्या हैं?
उत्तर:
प्रश्नों की कुल संख्या = 10
एक सही उत्तर के लिए अंक = 5
एक गलत उत्तर के लिए अंक = -2
अनुत्तरित प्रश्न के लिए अंक = 0
(i) मोहन के अंक = 4 × (5) + 6 × (-2)
= 20 + (-1)(6 × 2) = 20 – 12 = 8
(ii) रेशमा के अंक = 5 × (5) + 5 × (-2)
= 25 – 10 = 15
(iii) हीना का स्कोर = 2 × (5) + 5 × (-2) + 3 × 0
= 10 + (-10) + 0= 10 – 10 = 0
प्रश्न 8.
एक सीमेंट कंपनी को बेचे गए सफेद सीमेंट के प्रत्येक बैग पर ₹8 का लाभ और बेचे गए ग्रे सीमेंट के प्रत्येक बैग पर ₹5 की हानि होती है।
(a) कंपनी एक महीने में 3,000 बैग सफेद सीमेंट और 5,000 बैग ग्रे सीमेंट बेचती है। इसका लाभ या हानि क्या है?
(b) यदि बेचे गए ग्रे सीमेंट के बैगों की संख्या 6,400 है, तो कंपनी को न तो लाभ और न ही हानि होने के लिए सफेद सीमेंट के कितने बैग बेचने चाहिए?
उत्तर:
(a) कंपनी सफेद सीमेंट के 3,000 बैग बेचती है
∴ इसका लाभ = ₹ 3000 × 8 = ₹ 24000
इसके अलावा, कंपनी ग्रे सीमेंट के 5000 बैग बेचती है
∴ इसका नुकसान = ₹ 5000 × 5 = ₹ 25000
क्योंकि ₹ 25000 > 24,000
∴ कंपनी घाटे में है
हानि राशि = 25000 - 24,000
= ₹ 1000
(b) माना बेचे गए सफेद सीमेंट के बैगों की संख्या 'x' है।
दिया गया है: कोई लाभ नहीं और कोई हानि नहीं।
बेचे गए ग्रे बैगों की संख्या = 6400।
सफेद बैगों की संख्या × लाभ
= ग्रे बैगों की संख्या × हानि।
x × 8 = 6400 × 5
x =
∴ सफेद सीमेंट के बैगों की संख्या = 4000
प्रश्न 9.
इसे सत्य कथन बनाने के लिए रिक्त स्थान को पूर्णांक से बदलें।
(a) (-3) × …………. = 27
(b) 5 × …………. = -35
(c) ………… × (-8) = -56
(d) ………….. × (- 12) = 132
उत्तर:
(a) -3 × = 27
(-3) × (-9) = 27
(बी) 5 × = -35
5 × (-7) = -35
(सी) ………….. × (-8) = -56
7 × (-8) = -56
(घ) …………. × (-12) = 132
(-11) × (-12) = 132
Ex 1.4
प्रश्न 1.
निम्नलिखित में से प्रत्येक का मूल्यांकन करें:
(a) (-30) ÷ 10
(b) 50 ÷ (-5)
(c) (-36) ÷ (-9)
(d) (-49) ÷ (49)
(e) 13 ÷ [(-2) + 1]
(f) 0 ÷ (-12)
(g) [(-31) ÷ [(-30) + (-1)]
(h) [(-36) ÷ 12] ÷ 3
(i) = (-6 + 5) ÷ [(-2 + 1)]
उत्तर:
(a) (-30) ÷ 10 = – (30 ÷ 10) = – (3) = -3
(b) 50 ÷ (-5) = – (50 ÷ 5) = – (10) = -10
(c) (-36) ÷ (- 9) = + (36 ÷ 9) = + 4
(d) (-49) ÷ 49 = – (49 ÷ 49) = – (1) = -1
(e) 13 ÷ [(-2) + 1] = 13 ÷ (-2 + 1)
= 13 ÷ (-1) = - (13 ÷ 1) = -13
(f) 0 ÷ (-12) = – (0 ÷ 12) = 0
(g) (-31) ÷ [(-30) + (-1) = (-31) ÷ [-30 -1]
-31 ÷ (-31) = + (31 ÷ 31) = + 1
(h) [(-36) ÷ 12] ÷ 3 = [-36 ÷ 12] ÷ 3
= – (36 ÷ 12) ÷ 3 = – (3) ÷ 3
= -3 ÷ 3 = – 1
(i) [(-6) + 5] ÷ [(-2) + 1]
= (-6 + 5) ÷ (-2 + 1) = – 1 ÷ (-1)
= + (1 ÷ 1) = 1
प्रश्न 2.
सत्यापित करें कि a ÷ (b + c) ≠ (a ÷ b) + (a ÷ c) निम्नलिखित में से प्रत्येक a, b और c के मानों के लिए।
(a) a = 12, b = -4, c = 2
(b) a = (-10), b = 1, c = 1
उत्तर:
(a) दिया गया है a = 12, b = – 4 और c = 2
बायाँ पक्ष = a + (b + c)
= 12 ÷ (-4 + 2) = 12 ÷ (- 2)
= – [12 ÷ 2] = – 6
दायाँ पक्ष = (a ÷ b) + (a ÷ c)
= (12 + -4) + [12 ÷ 2]
= -(12 ÷ 4) + (6) = -3 + 6 = 3
∴ बायाँ पक्ष ≠ दायाँ पक्ष
(b) यहाँ a = – 10, b = 1, c = 1
बायाँ पक्ष = a ÷ (b + c)
= (-10) ÷ (1 + 1) = -10 ÷ 2
= -(10 ÷ 2) = -5
दायाँ पक्ष = (a ÷ b) + (a ÷ c)
= (-10 ÷ 1) + (-10 ÷ 1)
= -(10 ÷ 1) + (-10) ÷ 1
= -10 -10 = -20
बायाँ पक्ष ≠ दायाँ पक्ष
प्रश्न 3.
रिक्त स्थान भरें :
उत्तर:
(a) 369 ÷ 1 = 369 (a ÷ 1 = a)
(b) (-75) ÷ 75 = -1 (-a ÷ a = -1)
(c) (-206) ÷ 206 = 1 (- a) ÷ (-a) = 1
(d) -87 ÷ -1 = 87 (-a ÷ – 1 = a)
(e) -87 ÷ = -87 [(-a) ÷ 1 = -a]
(f) -48 ÷ 48 = -1 (-a ÷ a = -1)
(g) 20 ÷ -10 = -2
(h) -12 ÷ 4 = -3
प्रश्न 4.
पूर्णांकों (a, b) के पाँच युग्म लिखिए जिससे a ÷ b = -3 हो। ऐसा एक युग्म (6, -2) है क्योंकि 6 ÷ (-2) = (-3) है।
उत्तर:
पूर्णांकों (a, b) के पाँच युग्म लिखिए जिससे a ÷ b = -3 हो
(1) (3, -1)
(2) (-3, 1)
(3) (9, -3)
(4) (-9, 3)
(5) (-12, 4)
प्रश्न 5.
दोपहर 12 बजे तापमान शून्य से 10°C ऊपर था। यदि यह आधी रात तक 2°C प्रति घंटे की दर से घटता रहे, तो किस समय तापमान शून्य से 8°C नीचे होगा? आधी रात को तापमान कितना होगा?
उत्तर:
दोपहर 12 बजे तापमान = + 10°C
तापमान में परिवर्तन की दर = -2°C प्रति घंटा
दोपहर 12 बजे से आधी रात तक घंटों की संख्या = 12
∴ 12 घंटे में तापमान में परिवर्तन = 12° × (-2) = -24°C
मध्य रात्रि का तापमान = 10°C + (-24°C)
(अर्थात दोपहर 12 बजे के 12 घंटे बाद) = -14°C
+ 10°C और -8°C के बीच तापमान का अंतर = + 10°C - (-8°C)
= 10°C + 8°C = 18°C
समय लिया गया = 18 ÷ 2 = 9 घंटे
18°C का तापमान परिवर्तन दोपहर 12 बजे से 9 घंटे में होगा दोपहर
12 बजे से 9 घंटे बाद का समय = रात 9 बजे
प्रश्न 6.
एक कक्षा परीक्षा में प्रत्येक सही उत्तर के लिए (+3) अंक दिए जाते हैं और प्रत्येक गलत उत्तर के लिए (-2) अंक दिए जाते हैं और किसी भी प्रश्न का प्रयास न करने पर कोई अंक नहीं मिलता है।
(i) राधिका ने 20 अंक प्राप्त किए। यदि उसे 12 सही उत्तर मिले हैं, तो उसने कितने प्रश्नों का गलत प्रयास किया है?
(ii) मोहिनी ने इस
परीक्षा में -5 अंक प्राप्त किए, हालाँकि उसे 7 सही उत्तर मिले हैं। उसने कितने प्रश्नों का गलत प्रयास किया है?
उत्तर:
(i) माना कि राधिका द्वारा किए गए गलत प्रश्नों की संख्या 'x' है।
दिए गए प्रश्न के अनुसार, हम पाते हैं
(+3) × 12 + x × (-2) = 20
36 – 2x = 20
2x = 36 – 20
2x = 16
x = 8
(ii) माना कि मोहिनी द्वारा किए गए गलत प्रश्नों की संख्या 'x' है।
दिए गए प्रश्न के अनुसार, हम पाते हैं
(+3) × 7 + x × (-2) = -5
21 – 2x = -5
2x = 21 + 5
⇒ x =
इसलिए, मोहिनी ने 13 गलत प्रश्नों के उत्तर दिए।
प्रश्न 7.
एक लिफ्ट 6 मीटर/मिनट की दर से एक खदान की शाफ्ट में उतरती है। यदि उतरना जमीन से 10 मीटर ऊपर से शुरू होता है, तो इसे - 350 मीटर तक पहुँचने में कितना समय लगेगा।
हल:
दो स्थानों पर ऊंचाइयों में अंतर = 10 मीटर - (-350 मीटर) = 360 मीटर
उतरने की दर = 6 मीटर/मिनट
∴ लिया गया समय
इसलिए, लिफ्ट को पहुँचने में 1 घंटा लगेगा = 350 मीटर।
