NCERT Class 8 Maths Chapter 16 संख्याओं के साथ खेलना
NCERT Solutions for Class 8 Maths Chapter 16 संख्याओं के साथ खेलना
Ex 16.1
प्रश्न 1.
निम्नलिखित में से प्रत्येक में अक्षरों के मान ज्ञात कीजिए और चरणों के कारण बताइए।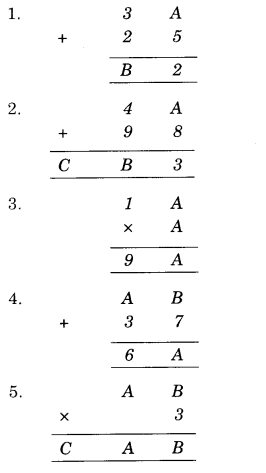
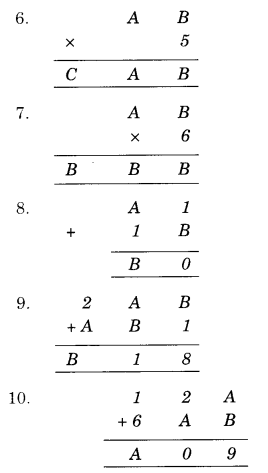
उत्तर:
1. आइए इकाई वाले कॉलम में योग देखें। यह A + 5 है और इससे हमें 2 प्राप्त होता है
(A + 5 = 7 + 5 = 12)। अतः, A का मान 7 होगा।
दहाई वाले कॉलम में योग के लिए, हमारे पास है
1 + 3 + 2 = B
∴ B = 6
प्रश्न 2.
यहाँ तीन अक्षर A, B और C हैं जिनके मान ज्ञात करने हैं।
उत्तर:
आइए इकाई वाले कॉलम में योग देखें।
यह A + 8 है और इससे हमें 3 प्राप्त होता है, इसलिए A का मान 5 होगा (A + 8 = 5 + 8 = 13)।
अब, दहाई वाले कॉलम में योग के लिए, हमारे पास है :
I + 4 + 9 = 14
∴ B = 4, C = 1
∴ दी गई पहेली हल हो गई है,
अर्थात A = 5, B = 4 और C = 1
प्रश्न 3.
A x A का इकाई अंक A है
उत्तर:
∴ A = 1 या 5 या 6
जब, A = 1
II ≠ 9A
∴ A ≠ 1
जब, A = 5
15 x 5 ≠ 9A;
∴ A ≠ 5
जब, A = 6
16 x 6 = 96
∴ A = 6
प्रश्न 4.
यहां, दो अक्षर A और B हैं जिनके मान ज्ञात करने हैं।
उत्तर:
B + 7, A देता है
और A + 3, 6 देता है।
संभावित मान 0 + 7 = 7
A = 7 लेकिन 7 + 3 ≠ 6 इसलिए यह स्वीकार्य नहीं है।
1 + 7 = 8
A = 8 लेकिन 8 + 3 ≠ 6 इसलिए स्वीकार्य नहीं है
2 + 7 = 9
A = 9 लेकिन 9 + 3 ≠ 6 इसलिए स्वीकार्य नहीं है
3 + 7= 10
A = 0 लेकिन 1+0 + 3 ≠ 6 इसलिए, स्वीकार्य नहीं है।
4 + 7= 11
A = 1 लेकिन 1 + 1 + 3 ≠ 6 इसलिए स्वीकार्य नहीं है।
5 + 7= 12
A = 2 साथ ही 1 + 2 + 3 = 6
तो B = 5 काम करता है और फिर हमें A के रूप में 2 मिलता है
∴ पहेली को नीचे दिखाए अनुसार हल किया गया है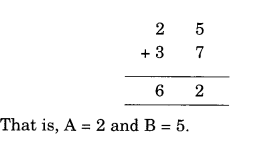
प्रश्न 5.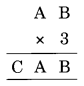
हल:
3 × B = B
⇒ B = D
3 × A = CA
⇒ 3 × 5 = 15
अतः A = 5 और C = 1
अतः A = 5, B = 0 और C = 1
प्रश्न 6.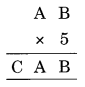
हल:
5 × B = B
⇒ B = 0 या 5
5 × A = CA
5 × 5 = 25
केवल तभी संभव है जब B = 0
इस प्रकार A = 5 और C = 2
इसलिए A = 5, B = 0 और C = 2
प्रश्न 7.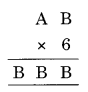
हल:
B × 6 = B
6 × 4 = 24 → B = 4 और 2 को
6 × A = BB तक बढ़ाया जाता है
⇒ 6 × 7 = 42 + 2 (आगे बढ़ाया गया) = 44
इस प्रकार B = 7
अतः A = 7 और B = 4
प्रश्न 8.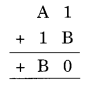
हल:
1 + B = 0
1 + 9 = 10 → इकाई अंक 0 है और 1 को A
+ 1 +1 तक ले जाया जाता है (आगे बढ़ाया गया) = B = 9
A + 2 = 9 ⇒ A = 9 – 2 = 7
अतः A = 7 और B = 9
प्रश्न 9.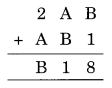
हल:
B + 1 = 8 ⇒ B = 8 – 1 = 7
A + B = इकाई अंक 1 वाली एक संख्या
A + B = 11
⇒ A + 7 = 11
⇒ A = 11 – 7 = 4 (1 आगे बढ़ा)
अब 1 आगे बढ़ा + 2 + A = B
3 + A = 7
⇒ A = 7 – 3 = 4
अतः A = 4, B = 7
प्रश्न 10.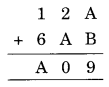
हल:
9 = A + B
9 = 1 + 8 या 2 + 7 या 3 + 6 या 4 + 5 या 8 + 1 या 7 + 2 या 6 + 3 या 5 + 4 या 0 + 9 या 9 + 0
अब इकाई के स्थान पर 0 आवश्यक है
2 + A = 10
⇒ A = 10 – 2 = 8
B = 9 – 8 = 1
1 + 6 + 1 (आगे बढ़ा) = A = 8
अतः A = 8 और B = 1
Ex 16.2
प्रश्न 1.
यदि 21y5, 9 का गुणज है, जहाँ y एक अंक है, तो y का मान क्या है?
उत्तर:
21Y5, 9 का गुणज है
∴ 2 + 1 + y + 5 = 8 + y, 9 से विभाज्य होना चाहिए
(8 + y) 9, 18, 27,… आदि होना चाहिए।
चूँकि y एक अंक है।
8 + y = 9
y = 9 – 8 = 1
∴ y का मान = 1.
प्रश्न 2.
यदि 31z5, 9 का एक गुणज है, जहाँ Z एक अंक है। z का मान क्या है? आप पाएंगे कि अंतिम प्रश्न के दो उत्तर हैं। ऐसा क्यों है?
उत्तर:
31z5 = 3 + l + z + 5 = 9 + z
31z5, 9 से विभाज्य है
∴ 9 + z, 9, 18, 27,… आदि के बराबर होना चाहिए।
Z एक अंकीय संख्या है।
9 + z इनमें से एक संख्या है।
9 + z = 9 तो z = 0
9 + z=18 तो nz= 18-9 = 9
∴ z का मान = 0 या 9।
प्रश्न 3.
यदि 24x, 3 का गुणज है, जहाँ x एक अंक है, तो x का मान क्या है?
हल:
चूँकि 24x, 3 का गुणज है, इसलिए अंकों 6 + x का योग 3 का गुणज है; इसलिए 6 + x इनमें से एक संख्या है; 0, 3, 6, 12, 15, 18, ……..
6 + x = 3k जहाँ k कोई पूर्णांक है।
k = 0 के लिए,
6 + x = 3 × 0
⇒ 6 + x = 0
x = -6. संभव नहीं है।
k = 1 के लिए,
6 + x = 3 × 1
⇒ 6 + x = 3
⇒ x = 3 – 6 = -3. संभव नहीं है
k = 2 के लिए,
6 + x = 3 × 2
⇒ 6 + x = 6
⇒ x = 6 – 6 = 0
2 + 4 + 0 = 6, 3 का गुणज है
k = 3 के लिए,
6 + x = 3 × 3
⇒ x = 9 – 6 = 3
2 + 4 + 3 = 9, 3 का गुणज है
k = 4 के लिए,
6 + x = 3 × 4
⇒ 6 + x = 12
⇒ x = 12 – 6 = 6
2 + 4 + 6 = 12 जो कि 3 का गुणज है
k = 5 के लिए,
6 + x = 3 × 5
⇒ x = 15 – 6 = 9
2 + 4 + 9 = 15 जो कि 3 का गुणज है
k = 6 के लिए,
6 + x = 3 × 6
⇒ x = 18 – 6 = 12 संभव नहीं है क्योंकि x अंक है
इसलिए x के आवश्यक मान 0, 3, 6 या 9 हैं।
प्रश्न 4.
यदि 31z5, 3 का एक गुणज है, जहाँ z एक अंक है, तो z का मान क्या होगा?
हल:
एक संख्या 3 का गुणज होती है यदि उसके अंकों का योग 3 से विभाज्य हो।
3 + 1 + z + 5 = 3k जहाँ k एक पूर्णांक है
⇒ 9 + z = 3k
⇒ z = 3k – 9
यहाँ, k = 0, 1, 2 संभव नहीं है क्योंकि z संख्या का एक अंक है।
k = 3 के लिए,
z = 3 × 3 – 9 = 9 – 9 = 0
9 + 0 = 9, 3 का गुणज
k = 4 के लिए,
z = 3 × 4 – 9 = 12 – 9 = 3
9 + 3 = 12, 3 का गुणज
k = 5 के लिए,
z = 3 × 5 – 9 = 15 – 9 = 6
9 + 6 = 15, 3 का गुणज
k = 6 के लिए,
z = 3 × 6 – 9 = 18 – 9 = 9
9 + 9 = 18, 3 का गुणज
k = 7 के लिए,
z = 3 × 7 – 9 = 21 – 9 = 12 संभव नहीं है क्योंकि z एक अंक है
इसलिए, 2 के आवश्यक मान 0, 3, 6 और 9 हैं।
