NCERT Class 8 Maths Chapter 15 रेखांकन का परिचय
NCERT Solutions for Class 8 Maths Chapter 15 रेखांकन का परिचय
Ex 15.1
प्रश्न 1.
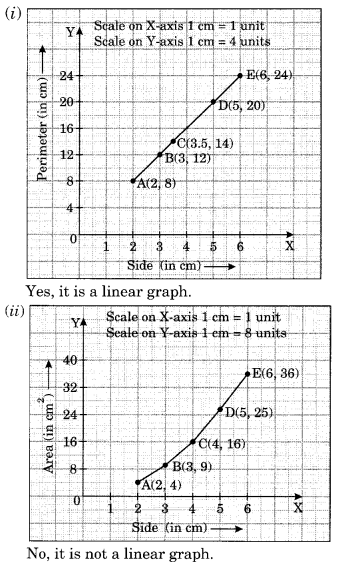
निम्नलिखित ग्राफ एक अस्पताल में एक मरीज के तापमान को दर्शाता है, जो हर घंटे दर्ज किया गया है।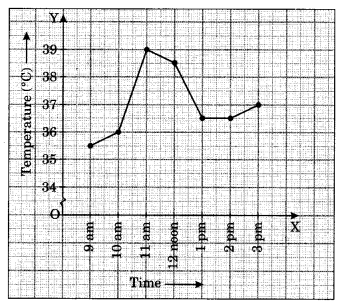
(a) दोपहर 1 बजे मरीज का तापमान क्या था?
(b) मरीज का तापमान 38.5°C कब था?
(c) दी गई अवधि के दौरान मरीज का तापमान दो बार समान था। वे दोनों बार क्या थे?
(d) दोपहर 1:30 बजे तापमान क्या था? आप अपने उत्तर पर कैसे पहुंचे?
(e) किस अवधि के दौरान मरीज के तापमान में वृद्धि देखी गई?
हल:
(a) दोपहर 1 बजे मरीज का तापमान 36.5°C था
(b) दोपहर 12:00 बजे मरीज का तापमान 38.5°C था।
(c) दोपहर 1 बजे और 2 बजे मरीज का तापमान 36.5°C था।
(d) दोपहर 1:30 बजे तापमान 36.5°C था। हमने दोपहर 1 बजे का मध्य मान लिया है। और दोपहर 2 बजे, यानी 1:30 बजे और 36.5 डिग्री सेल्सियस दिखाने वाली क्षैतिज रेखा से मिलने के लिए लंबवत ऊपर की ओर बढ़ें।
(ई) सुबह 9 बजे से 10 बजे और सुबह 10 बजे से 11 बजे के दौरान, तापमान में ऊपर की ओर प्रवृत्ति देखी गई।
प्रश्न 2.
निम्नलिखित रेखा आलेख एक विनिर्माण कंपनी के वार्षिक विक्रय के आंकड़े दर्शाता है।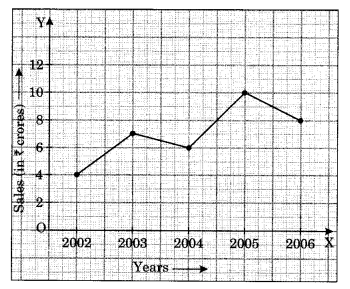
(a) (i) 2002 (ii) 2006 में बिक्री क्या थी?
(b) (i) 2003 (ii) 2005 में बिक्री क्या थी?
(c) 2002 और 2006 में बिक्री के बीच अंतर की गणना करें।
(d) किस वर्ष में बिक्री के बीच उसके पिछले वर्ष की तुलना में सबसे बड़ा अंतर था?
हल:
(a) वर्ष 2002 में बिक्री ₹ 4 करोड़ थी और वर्ष 2006 में ₹ 8 करोड़ थी।
(b) वर्ष 2003 में बिक्री ₹ 7 करोड़ थी और 2005 में ₹ 10 करोड़ थी।
(c) 2002 में बिक्री = ₹ 4 करोड़
2006 में बिक्री = ₹ 8 करोड़
अंतर = ₹ (8 – 4) करोड़ = ₹ 4 करोड़।
(d) पिछले वर्ष की तुलना में बिक्री के बीच सबसे बड़ा अंतर वर्ष 2005 में था।
प्रश्न 3.
वनस्पति विज्ञान के एक प्रयोग के लिए, दो अलग-अलग पौधे, पौधे A और पौधे B, समान प्रयोगशाला स्थितियों में उगाए गए थे। उनकी ऊँचाइयों को प्रत्येक सप्ताह के अंत में 3 सप्ताह तक मापा गया। परिणाम निम्नलिखित ग्राफ द्वारा दिखाए गए हैं।
(a) पौधे A की ऊँचाई (i) 2 सप्ताह (ii) 3 सप्ताह के बाद कितनी थी
(b) पौधे B की ऊँचाई (i) 2 सप्ताह (ii) 3 सप्ताह के बाद कितनी थी
(c) तीसरे सप्ताह के दौरान पौधे A की वृद्धि कितनी हुई?
(d) दूसरे सप्ताह के अंत से तीसरे सप्ताह के अंत तक पौधे B की वृद्धि कितनी हुई?
(e) किस सप्ताह के दौरान पौधे A की वृद्धि सबसे अधिक हुई?
(f) किस सप्ताह के दौरान पौधे B की वृद्धि सबसे कम हुई?
(g) क्या यहाँ दिखाए गए किसी भी सप्ताह के दौरान दोनों पौधे समान ऊँचाई के थे? निर्दिष्ट करें।
हल:
(a) पौधे A की ऊँचाई (i) 2 सप्ताह के बाद 7 सेमी थी (ii) 3 सप्ताह के बाद 9 सेमी थी।
(b) पौधे B की ऊँचाई (i) 2 सप्ताह बाद 7 सेमी थी (ii) 3 सप्ताह बाद 10 सेमी थी।
(c) पौधे A की ऊँचाई 7 सेमी से 9 सेमी अर्थात 2 सेमी बढ़ी।
(d) पौधे B की ऊँचाई 7 सेमी से 10 सेमी अर्थात 3 सेमी बढ़ी।
(e) पौधे A की वृद्धि दूसरे सप्ताह में सबसे अधिक अर्थात 5 सेमी हुई।
(f) पौधे B की वृद्धि पहले सप्ताह में सबसे कम अर्थात 1 सेमी हुई।
(g) हाँ, दोनों पौधों की वृद्धि दूसरे सप्ताह के अंत में समान ऊँचाई अर्थात 7 सेमी हुई।
प्रश्न 4.
निम्नलिखित ग्राफ एक सप्ताह के प्रत्येक दिन के लिए पूर्वानुमानित तापमान और वास्तविक तापमान को दर्शाता है।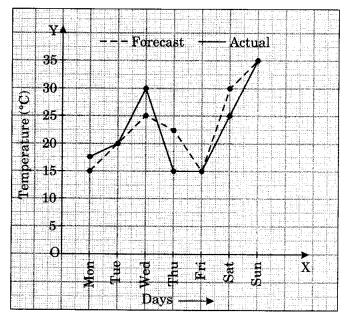
(a) किन दिनों का पूर्वानुमानित तापमान वास्तविक तापमान के समान था?
(b) सप्ताह के दौरान अधिकतम पूर्वानुमानित तापमान क्या था?
(c) सप्ताह के दौरान न्यूनतम वास्तविक तापमान क्या था?
(d) किस दिन वास्तविक तापमान पूर्वानुमानित तापमान से सबसे अधिक भिन्न था?
हल:
(a) मंगलवार, शुक्रवार और रविवार को पूर्वानुमानित तापमान वास्तविक तापमान के समान था, अर्थात क्रमशः 20°C, 15°C और 35°C।
(b) सप्ताह के दौरान पूर्वानुमानित अधिकतम तापमान 35°C था। (c) सप्ताह के दौरान न्यूनतम वास्तविक तापमान 17.5°C था। (d) गुरुवार को, वास्तविक तापमान पूर्वानुमानित तापमान से सबसे अधिक भिन्न था , अर्थात 22.5°C - 15°C = 7.5°C।
प्रश्न 5.
नीचे दी गई तालिकाओं का उपयोग करके रैखिक आलेख खींचिए।
(a) विभिन्न वर्षों में एक पहाड़ी शहर में बर्फबारी के दिनों की संख्या।
(b) विभिन्न वर्षों में एक गाँव में पुरुषों और महिलाओं की जनसंख्या (हजारों में)।
उत्तर:
(a) रैखिक ग्राफ विभिन्न वर्षों में हुई बर्फबारी को दर्शाता है।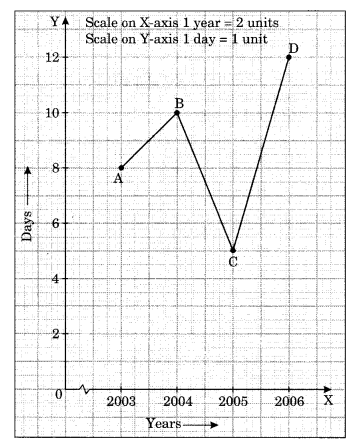
(b) विभिन्न वर्षों में एक गाँव में पुरुषों और महिलाओं की जनसंख्या को दर्शाने वाला रैखिक ग्राफ: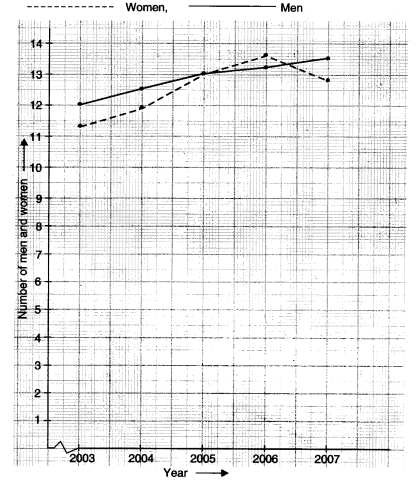
प्रश्न 6.
एक कूरियर व्यक्ति व्यापारी को पार्सल देने के लिए शहर से पड़ोसी उपनगरीय क्षेत्र में साइकिल चलाता है। विभिन्न समयों पर शहर से उसकी दूरी निम्नलिखित ग्राफ द्वारा दर्शाई गई है।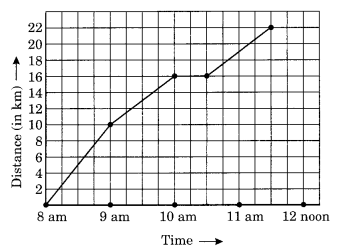
(a) समय अक्ष के लिए क्या पैमाना लिया गया है?
(b) व्यक्ति ने यात्रा में कितना समय लिया?
(c) व्यापारी का स्थान शहर से कितनी दूर है?
(d) क्या व्यक्ति अपने रास्ते में रुका था? व्याख्या करें?
(e) किस अवधि के दौरान उसने सबसे तेज साइकिल चलाई?
हल:
(a) समय-अक्ष पर लिया गया पैमाना अर्थात, x-अक्ष 4 इकाई = 1 घंटा है
(b) कुल यात्रा के लिए व्यक्ति द्वारा लिया गया कुल समय 3 घंटे 30 मिनट है।
(c) व्यापारी का स्थान शहर से 22 किमी दूर है।
(d) हाँ, यह ग्राफ के क्षैतिज भाग द्वारा स्पष्ट रूप से इंगित किया गया है कि व्यक्ति सुबह 10 बजे से 10:30 बजे तक रुका था।
(e) वह सुबह 8 बजे से 9 बजे के बीच सबसे तेज साइकिल चलाता था।
प्रश्न 7.
क्या निम्नलिखित रूप में समय-तापमान ग्राफ हो सकता है? अपने उत्तर का औचित्य सिद्ध कीजिए।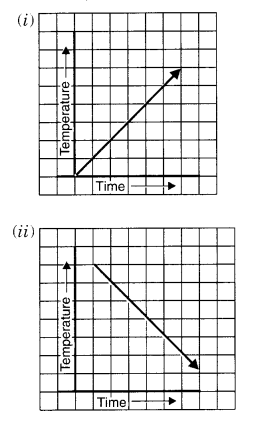
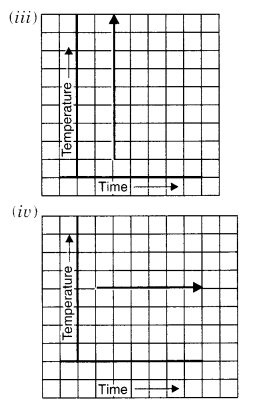
हल:
(i) हाँ; यह हो सकता है
यह एक समय-तापमान ग्राफ दिखाता है। यह समय के साथ तापमान में वृद्धि दर्शाता है।
(ii) हाँ; यह हो सकता है
यह एक समय-तापमान ग्राफ दिखाता है।
यह समय के साथ तापमान में कमी दर्शाता है।
(iii) यह एक समय-तापमान ग्राफ नहीं हो सकता क्योंकि यह एक विशेष समय पर अनंत रूप से कई अलग-अलग तापमान दिखाता है जो संभव नहीं है।
(iv) हाँ; यह हो सकता है
यह एक समय-तापमान ग्राफ दिखाता है।
यह अलग-अलग समय पर एक निश्चित तापमान दिखाता है।
Ex 15.2
प्रश्न 1.
निम्नलिखित बिंदुओं को एक ग्राफ शीट पर अंकित कीजिए। सत्यापित कीजिए कि क्या वे एक रेखा पर स्थित हैं।
(a) A (4, 0), B(4, 2), C(4, 6), D(4, 2.5)
(b) P(1, 1), Q(2, 2), R(3, 3), S(4, 4)
(c) K(2, 3), L(6, 3), M(5, 5), N (2, 5)
हल: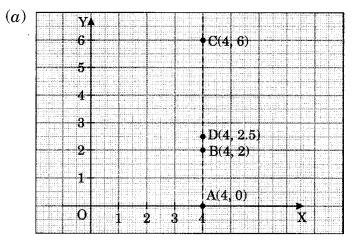
हाँ, सभी निर्देशांक बिंदु एक रेखा पर स्थित हैं।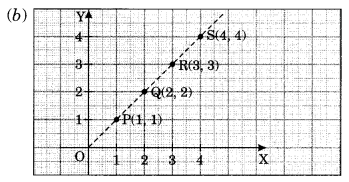
हाँ, सभी निर्देशांक बिंदु एक रेखा पर स्थित हैं।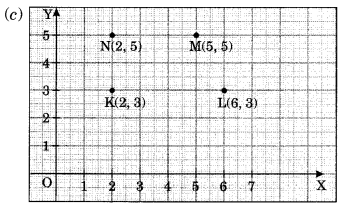
नहीं, निर्देशांक बिंदु एक रेखा पर स्थित नहीं हैं।
प्रश्न 2.
(2, 3) और (3, 2) से होकर जाने वाली रेखा खींचिए। उन बिंदुओं के निर्देशांक ज्ञात कीजिए जहाँ यह रेखा x-अक्ष और y-अक्ष को मिलती है।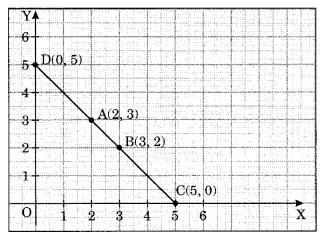
हल:
CD वह वांछित रेखा है जो बिंदुओं A(2, 3), B (3, 2) से होकर जाती है और x-अक्ष को C(5, 0) और y-अक्ष को D(0, 5) पर मिलती है।
प्रश्न 3.
इन आसन्न आकृतियों में से प्रत्येक के शीर्षों के निर्देशांक लिखिए।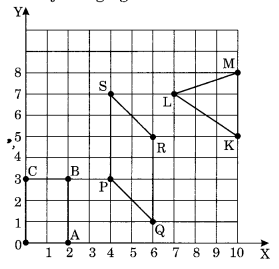
उत्तर:
(i) 'O' के निर्देशांक (0,0) हैं, A के निर्देशांक (2,0) हैं, B के निर्देशांक (2, 3) हैं और C के निर्देशांक (0, 3) हैं।
(ii) P के निर्देशांक (4, 3) हैं, Q के निर्देशांक (6, 1) हैं, R के निर्देशांक (6, 5) हैं, S के निर्देशांक (4, 7) हैं।
(iii) K के निर्देशांक (10, 5) हैं, L के निर्देशांक (7, 7) हैं और M के निर्देशांक (10, 8) हैं।
प्रश्न 4.
बताइए कि कौन सा कथन सत्य है या असत्य। यदि वे असत्य हैं तो सही करें।
(i) एक बिंदु जिसका x-निर्देशांक शून्य है और y-निर्देशांक शून्य नहीं है, y-अक्ष पर स्थित होगा।
(ii) एक बिंदु जिसका y-निर्देशांक शून्य है और x-निर्देशांक 5 है, y-अक्ष पर स्थित होगा।
(iii) मूल बिंदु के निर्देशांक (0,0) हैं।
उत्तर:
(i) सत्य
(ii) असत्य: एक बिंदु जिसका y-निर्देशांक शून्य है और x-निर्देशांक 5 है, x-अक्ष पर स्थित होगा।
(iii) सत्य
Ex 15.3
प्रश्न 1.
निम्नलिखित मानों की तालिकाओं के लिए अक्षों पर उपयुक्त पैमाने के साथ ग्राफ बनाएं
(a) सेब की कीमत
(b) कार द्वारा तय की गई दूरी
(i) सुबह 7.30 बजे से 8 बजे के बीच कार ने कितनी दूरी तय की?
(ii) कार ने चलने के बाद से 100 किमी की दूरी कब तय की थी?
(c) एक वर्ष के लिए जमा पर ब्याज।
(i) क्या ग्राफ मूल बिंदु से होकर गुजरता है?
(ii) ब्याज ज्ञात करने के लिए ग्राफ का उपयोग करें? एक वर्ष के लिए 2500।
(iii) ₹ 280 प्रति वर्ष ब्याज प्राप्त करने के लिए कितना पैसा जमा करना होगा?
उत्तर:
(a) (i) x-अक्ष और y-अक्ष को एक दूसरे के लंबवत खींचें।
(ii) एक उपयुक्त पैमाना लें (x-अक्ष; 1 सेमी = 1 इकाई) (y-अक्ष; 1 सेमी = 5 इकाई)
(iii) x-अक्ष के साथ सेबों की संख्या लें और y-अक्ष के साथ ₹ में लागत को चिह्नित करें।
(iv) बिंदुओं (1,5), (2,10) को प्लॉट करें; (3,15): (4, 20) और (5,25)
(v) बिंदुओं को मिलाने पर, हम ग्राफ को एक सरल रेखा के रूप में प्राप्त करते हैं।
(b) (i) x-अक्ष और y-अक्ष को एक दूसरे के लंबवत खींचें।
(ii) x-अक्ष और y-अक्ष के साथ उपयुक्त पैमाना चुनें (x-अक्ष; lcm = 1 इकाई; y-अक्ष; lcm = 20 इकाई।
(iii) x-अक्ष के साथ समय (घंटों में) और y-अक्ष के साथ दूरी (किमी में) अंकित करें।
(iv) बिंदु (6, 40), (7, 80) (8, 120) और (9, 160) को आलेखित करें।
(v) बिंदुओं को मिलाकर, हमें आवश्यक ग्राफ प्राप्त होता है।
1. ग्राफ में, x-अक्ष पर सुबह 7:30 बजे को इंगित करने वाले बिंदु पर एक लंबवत खींचें जैसे कि यह ग्राफ को A पर मिलता है। A से 100 किमी पर y-अक्ष से मिलने के लिए x-अक्ष के समानांतर एक रेखा खींचें।
सुबह 7.30 बजे और 8:00 बजे के बीच तय की गई दूरी।
= (120 किमी - 80 किमी) 20 किमी
2. जिस समय कार ने अपनी शुरुआत के बाद से 100 किमी की दूरी तय की थी वह सुबह 7.30 बजे था
(c) (i) x-अक्ष और y-अक्ष को परस्पर लंबवत खींचें।
(ii) एक उपयुक्त पैमाना लें [x-अक्ष 1 सेमी = ₹ 1000 और y-अक्ष lcm ? 40] x-अक्ष के साथ जमा को चिह्नित करें और y-अक्ष के साथ ब्याज को चिह्नित करें।
(iii) बिंदुओं को प्लॉट करें और एक सीधी रेखा प्राप्त करने के लिए बिंदुओं को मिलाएं।
उत्तर:
(i) हाँ, यह मूल बिंदु से होकर गुजरती है।
(ii) ग्राफ से, ₹ 2500 पर ब्याज ₹ 200 है।
(iii) ग्राफ से, ₹ 280 का ब्याज प्राप्त करने के लिए ₹ 3500 जमा करने चाहिए।
प्रश्न 2.
निम्नलिखित के लिए आलेख खींचिए: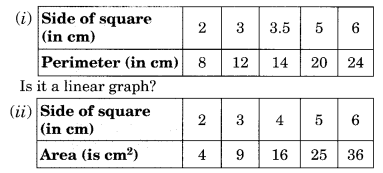
हल: