NCERT Class 8 Maths Chapter 14 गुणनखंडन
NCERT Solutions for Class 8 Maths Chapter 14 गुणनखंडन
Ex 14.1
प्रश्न 1.
दिए गए पदों के सार्व गुणनखंड ज्ञात कीजिए।
(i) 12x, 36
(ii) 2y, 22xy
(iii) 14pq, 28p 2 q 2
(iv) 2x, 3x 2 , 4
(v) 6abc, 24ab 2 , 12a 2 b
(vi) 16x 3 , -4x 2 , 32x
(vii) 10pq, 20qr, 30rp
(viii) 3x 2 y 3 , 10x 3 y 2 , 6x 2 y 2 z
हल:
(i) 12x, 36
(2 × 2 × 3 × x) और (2 × 2 × 3 × 3)
सामान्य कारक 2 × 2 × 3 = 12 हैं
इसलिए, सामान्य कारक = 12
(ii) 2y, 22xy
= (2 × y) और (2 × 11 × x × y)
उभयनिष्ठ गुणनखंड 2 × y = 2y हैं।
अतः, उभयनिष्ठ गुणनखंड = 2y
(iii) 14pq, 28p 2 q 2
= (2 × 7 × p × q) और (2 × 2 × 7 × p × p × q × q)
सामान्य कारक 2 × 7 × p × q = 14pq हैं
इसलिए, सामान्य कारक = 14pq
(iv) 2x, 3x 2 , 4
= (2 × x), (3 × x × x) और (2 × 2)
उभयनिष्ठ गुणनखंड 1 है।
अतः, उभयनिष्ठ गुणनखंड = 1 [∵ 1 प्रत्येक संख्या का एक गुणनखंड है]
(v) 6abc, 24ab 2 , 12a 2 b
= (2 × 3 × a × b × c), (2 × 2 × 2 × 3 × a × b × b) और (2 × 2 × 3 × a × a × b)
सामान्य कारक 2 × 3 × a × b = 6ab हैं
इसलिए, सामान्य कारक = 6ab
(vi) 16x 3 , -4x 2 , 32x
= (2 × 2 × 2 × 2 × x × x × x), -(2 × 2 × x × x), (2 × 2 × 2 × 2 × x)
सामान्य कारक 2 × 2 × x = 4x हैं
इसलिए, सामान्य कारक = 4x
(vii) 10pq, 20qr, 30rp
= (2 × 5 × p × q), (2 × 2 × 5 × q × r), (2 × 3 × 5 × r × p)
सामान्य कारक 2 × 5 = 10 हैं
इसलिए, सामान्य कारक = 10
(viii) 3x 2 y 2 , 10x 3 y 2 , 6x 2 y 2 z
= (3 × x × x × y × y), (2 × 5 × x × x × x × y × y), (2 × 3 × x × x × y × y × z)
सामान्य कारक x × x × y × y = x 2 y 2
इसलिए, सामान्य कारक = x 2 y 2 ।
प्रश्न 2.
निम्नलिखित व्यंजकों के गुणनखंड कीजिए।
(i) 7x – 42
(ii) 6p – 12q
(iii) 7a 2 + 14a
(iv) – 16 z + 20 z 3
(v) 20 l 2 m + 30 alm
(vi) 5x 2 y – 15xy 2
(vii) 10a 2 + 15 b 2 + 20c 2
(viii) – 4a 2 + 4ab – 4ca
(ix) x 2 yz + xyz 2 xy 2 z xyz 2
(x) ax 2 y + bxy 2 + cxyz
उत्तर:
(i) 7x – 42
=7 xx – 2 x 3 x 7
= 7 (x – 2 x 3)
= 7 (x – 6)
(ii) 6p – 12q
= 2 x 3p – 2 x 2 x 3 xq
= 2 x 3 [p – 2 xq]
= 6 (p – 2q)
(iii) 7a2 + 14a
=7 x a x a + 2 x 7 x a
= 7a (a + 2)
(iv) – 16z + 20 z3
= -2 x 2 x 2 x 2 x z + 2 x 2 x 5 x z x z x z
= 2 x 2 x z [-2x2 + 5 x z x z]
= 4z (-4 + 5z2)
(v) 20 l2m + 30 alm
= 2 x 2 x 5 x l x l x m + 2 x 3 x 5 x a x l x m
= 2 x 5 x l x m[2 x l + 3a]
= 10lm (2l + 3a)
(vi) 5x2y-15xy2
=5 x x x x x y – 3 x 5 x x x y x x
= 5xy (x – 3y)
(vii) 10a2 – 15b2 + 20c2
= 2 x 5 x a x a – 3 x 5 x b x b + 2 x 2 x 5 x c x c
= 5[2 x a x a – 3 x b x b + 2 x 2 x c x c]
= 5 (2a2 – 3b2 + 4c2)
(viii) -4a2 + 4ab – 4ca
= -2 x 2 x a x a + 2 x 2 x a x b – 2 x 2 x c x a
= 2 x 2 x a (-a + b – c)
= 4a (-a + b – c)
(ix) x2yz + xy2z + xyz2
= x x x x y x z + x x y x y x z + x x y x z x z
= x x y x z[x + y + z]
= xyz (x + y + z)
(x) ax2y + bxy2 + cxyz
= a x x x x x y + b x x x y x y + c x x x y x z
= x x y[a x x + b x y + c x z]
= xy (ax + by + cz)
प्रश्न 3.
गुणनखंड कीजिए
(i) x 2 + xy + 8x + 8y
(ii) 15xy – 6x + 5y – 2
(iii) ax + bx – ay – द्वारा
(iv) 15pq + 15 + 9q – 25p
(v) z – 7 + 7xy – xyz
उत्तर:
(i) x 2 + xy + 8x + 8y
= x(x + y) + 8 (x + y)
= (x + y) (x + 8)
(ii) 15xy - 6x + 5y - 2
= 3x (5y - 2) + 1 (5y - 2)
= (5y - 2) (3x + 1)
(iii) ax + bx – ay – by
= x (a + b) – y (a + b)
= (a + b) (x – y)
(iv) 15pq + 15 + 9q + 25p
= 15pq + 25p + 9q + 15
= 5p (3q + 5) + 3 (3q + 5)
(पदों को पुनः व्यवस्थित करने पर)
= (3q + 5) (5p + 3)
(v) z – 7 + 7xy – xyz
= z – xyz + 7xy – 7
= z( 1 – xy) + (7 (xy – 1)
(पदों को पुनः व्यवस्थित करने पर)
= z (1 – xy) – 7 (1 – xy)
= (1 – xy) (z- 7)
Ex 14.2
प्रश्न 1.
निम्नलिखित व्यंजकों के गुणनखंड कीजिए।
(i) a 2 + 8a + 16
(ii) p 2 – 10p + 25
(iii) 25m 2 + 30m + 9
(iv) 49y 2 + 84yz + 36z 2
(v) 4x 2 – 8x + 4
(vi) 121b 2 – 88bc + 16c 2
(vii) (l + m) 2 – 4lm. (संकेत: पहले (l + m) 2
का विस्तार करें) (viii) a 4 + 2a 2 b 2 + b 4
हल:
(i) a 2 + 8a + 16
यहाँ, 4 + 4 = 8 और 4 × 4 = 16
a 2 + 8a +16
= a 2 + 4a + 4a + 4 × 4
= (a 2 + 4a) + (4a + 16)
= a(a + 4) + 4(a + 4)
= (a + 4) (a + 4)
= (a + 4) 2
(ii) p 2 – 10p + 25
यहाँ, 5 + 5 = 10 और 5 × 5 = 25
p 2 – 10p + 25
= p 2 – 5p – 5p + 5 × 5
= (p 2 – 5p) + (-5p + 25)
= p(p – 5) – 5(p – 5)
= (p – 5) (p – 5)
= (p – 5) 2
(iii) 25 मी 2 + 30 मी + 9
यहाँ, 15 + 15 = 30 और 15 × 15 = 25 × 9 = 225
25 मी 2 + 30 मी + 9
= 25 मी 2 + 15 मी + 15 मी + 9
= (25 मी 2 + 15 मी) + (15 मी + 9)
= 5 मी(5 मी + 3) + 3(5 मी + 3)
= (5 मी + 3) (5 मी + 3)
= (5 मी + 3) 2
(iv) 49y 2 + 84yz + 36z 2
यहाँ, 42 + 42 = 84 और 42 × 42 = 49 × 36 = 1764
49y 2 + 84yz + 36z 2
= 49y 2 + 42yz + 42yz + 36z 2
= 7y(7y + 6z) +6z(7y + 6z)
= (7y + 6z) (7y + 6z)
= (7y + 6z) 2
(v) 4x 2 – 8x + 4
= 4(x 2 – 2x + 1) [4 को उभयनिष्ठ लेते हुए]
= 4(x 2 – x – x + 1)
= 4[x(x – 1) -1(x – 1)]
= 4(x – 1)(x – 1)
= 4(x – 1) 2
(vi) 121b 2 – 88bc + 16c 2
यहाँ, 44 + 44 = 88 और 44 × 44 = 121 × 16 = 1936
121b 2 – 88bc + 16c 2
= 121b 2 – 44bc – 44bc + 16c 2
= 11b(11b – 4c) – 4c(11b – 4c)
= (11b – 4c) (11b – 4c)
= (11b – 4c) 2
(vii) (l + m) 2 – 4lm
(l + m) 2 का विस्तार करने पर , हम पाते हैं
l 2 + 2lm + m 2 – 4lm
= l 2 – 2lm + m 2
= l 2 – Im – lm + m 2
= l(l – m) – m(l – m)
= (l – m) (l – m)
= (l – m) 2
(viii) a 4 + 2a 2 b 2 + b 4
= a 4 + a 2 b 2 + a 2 b 2 + b 4
= a 2 (a 2 + b 2 ) + b 2 (a 2 + b 2 )
= (a 2 + b 2 )(a 2 + b 2 )
= (a 2 + b 2 ) 2
प्रश्न 2.
गुणनखंड कीजिए
(i) 4p 2 – 9q 2
(ii) 63a 2 – 112b 2
(iii) 49x 2 – 36
(iv) 16x 5 – 144x 3
(v) (l + m) 2 – (l – m) 2
(vi) 9x 2 y 2 – 16
(vii) (x 2 – 2xy + y 2 ) – z 2
(viii) 25a 2 – 4b 2 + 28bc – 49c 2
उत्तर:
(i) 4p 2 – 9q 2
= (2p) 2 – (3q) 2
= (2p + 3q) (2p – 3q)
[a 2 – b 2 = (a + b) (a – b)]
(ii) 63a2-112b2
= 7 x (9a2 – 16b2)
= 7[(3a)2 – (4b)2 ]
= 7 (3a + 4b) (3a – 4b)
[a2 – b2 = (a + b) (a – b)]
(iii) 49x2 – 36
= (7x)2 – 62 = (7x + 6) (7x – 6)
[Using a2 – b2 = (a + b) (a – b)]
(iv) 16x3 – 144x3
= x3 [16×2 – 144]
= x3 x 16 [x2 – 9]
= 16x3 [x2 – 32]
= 16x3 (x + 3) (x – 3)
(v) (l + m)2 – (l – m)2
= (l + m + l – m) [l + m – (l – m)]
= 2l [l + m – l + m]
= 2l x 2m = 4lm
(vi) 9x2y2 – 16
= (3xy)2 – 42
= (3xy + 4) (3xy – 4)
(vii) (x2 – 2xy + y2) – z2
= [x2 – 2xy + y2] – z2
= (x – y)2 – z2
= (x – y + z) (x – y – z)
(viii) 25a2 – 4b2 + 28bc – 49c2
= 25a2 – [4b2 – 28bc + 49c2 ]
= (5a)2 – [(2b)2 – 2 x 2b x 7c + (7c)2]
= (5a)2 – (2b – 7c)2
= (5a + 2b – 7c) [5a – (2b – 7c)]
= (5a + 2b – 7c)(5a – 2b + 7c)
प्रश्न 3.
भावों का गुणनखंड कीजिए।
(i) ax 2 + bx
(ii) 7p 2 + 21q 2
(iii) 2x 3 + 2xy 2 + 2xz 2
(iv) am 2 + bm 2 + bn 2 + an 2
(v) (lm + 1) + m + 1
(vi) y (y + z) + 9 (y + z)
(vii) 5y 2 - 20y - 8z + 2yz
(viii) 10ab + 4a + 5b + 2
(ix) 6xy – 4y + 6 – 9x
उत्तर:
(i) ax 2 + bx
= axxxx + bxx
= x (ax + b)
(ii) 7p 2 + 21q 2
= 7 xpxp + 3 x 7 xqxq – 7 (p 2 + 3q 2 )
(iii) 2x 3 + 2xy 2 + 2xz 2
= 2 xxxxxx + 2 xxxyxy + 2 xxxzxz
= 2x(x xx + yxy + zxz)
= 2x (x 2 + y 2 + z 2 )
(iv) am 2 + bm 2 + bn 2 + an 2
= m 2 (a + b) + n 2 (b + a)
= m 2 (a + b) + n 2 (a + b)
= (a + b) (m 2 + n 2 )
(v) (lm + l) + m + l
= l(m + l) + l(m + l)
= (m + l) (l + l)
(vi) y (y + z) + 9 (y + z)
= (y + z) (y + 9)
[(y + z) is common for both terms)]
(vii) 5y2 – 20y – 8z + 2yz
= 5y x y – 4 x 5y – 2 x 2 x 2 x z + 2 x y x z
= 5y (y – 4) + 2z (- 4 + y)
= 5y (y – 4) + 2z (y – 4)
= (y – 4) (5y + 2z)
(viii) 10ab + 4a + 5b + 2
= 2 x 5 x a x b + 2 x 2 x a + 5 x b + 2
= 2a (5b + 2) + 1 (5b + 2)
= (5b + 2) (2a + 1)
(ix) 6xy – 4y + 6 – 9x
= 2 x 3 x x x y – 2 x 2 x y + 2 x 3 – 3 x 3 x x
= 2y (3x – 2) + 3 (2 – 3x)
= 2y (3x – 2) – 3 (3x – 2)
= (3x – 2) (2y – 3)
प्रश्न 4.
गुणनखंड कीजिए।
(i) a 4 – b 4
(ii) p 4 – 81
(iii) x 4 – (y + z) 4
(iv) x 4 – (x – z) 4
(v) a 4 – 2a 2 b 2 + b 4
हल:
(i) a 4 – b 4 – (a 2 ) 2 – (b 2 ) 2
[∵ a 2 – b 2 = (a – b)(a + b)]
= (a 2 – b 2 ) (a 2 + b 2 )
= (a – b) (a + b) (a 2 + b 2 )
(ii) p4 – 81 = (p2)2 – (9)2
= (p2 – 9) (p2 + 9)
[∵ a2 – b2 = (a – b)(a + b)]
= (p – 3)(p + 3) (p2 + 9)
(iii) x4 – (y + z)4 = (x2)2 – [(y + z)2]2
[∵ a2 – b2 = (a – b)(a + b)]
= [x2 – (y + z)2] [x2 + (y + z)2]
= [x – (y + z)] [x + (y + z)] [x2 + (y + z)2]
= (x – y – z) (x + y + z) [x2 + (y + z)2]
(iv) x4 – (x – z)4 = (x2)2 – [(y – z)2]2
= [x2 – (y – z)2] [x2 + (y – z)2]
= (x – y + z) (x + y – z) (x2 + (y – z)2]
(v) a4 – 2a2b2 + b4
= a4 – a2b2 – a2b2 + b4
= a2(a2 – b2) – b2(a2 – b2)
= (a2 – b2)(a2 – b2)
= (a2 – b2)2
= [(a – b) (a + b)]2
= (a – b)2 (a + b)2
प्रश्न 5.
निम्नलिखित व्यंजकों के गुणनखंड कीजिए।
(i) p 2 + 6p + 8
(ii) q 2 – 10q + 21
(iii) p 2 + 6p – 16
हल:
(i) p 2 + 6p + 8
यहाँ, 2 + 4 = 6 और 2 × 4 = 8
p 2 + 6p + 8
= p 2 + 2p + 4p + 8
= p (p + 2) + 4(p + 2)
= (p + 2) (p + 4)
(ii) q 2 – 10q + 21
यहाँ, 3 + 7 = 10 और 3 × 7 = 21
q 2 – 10q + 21
= q 2 – 3q – 7q + 21
= q(q – 3) – 7(q – 3)
= (q – 3) (q – 7)
(iii) p 2 + 6p – 16
यहाँ, 8 – 2 = 6 और 8 × 2 = 16
p 2 + 6p – 16
= p 2 + 8p – 2p – 16
= p(p + 8) – 2(p + 8)
= (p + 8) (p – 2)
Ex 14.3
प्रश्न 1.
निम्नलिखित विभाजन करें।
(i) 28x 4 ÷ 56x
(ii) -36y 3 ÷ 9y 2
(iii) 66pq 2 r 3 ÷ 11qr 2
(iv) 34x 3 y 3 z 3 ÷ 51xy 2 z 3
(v) 12a 8 b 8 ÷ (-6a 6 b 4 )
हल: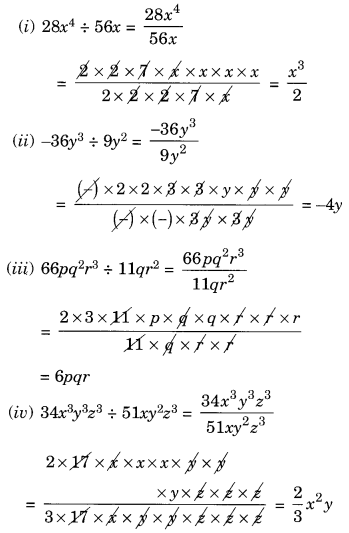
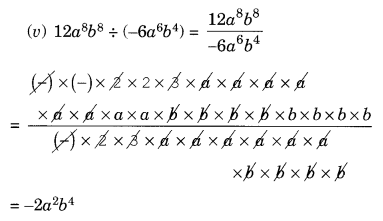
प्रश्न 2.
निम्नलिखित बहुपद को दिए गए एकपदी से भाग दें।
(i) (5x 2 – 6x) ÷ 3x
(ii) (3y 8 – 4y 6 + 5y 4 ) ÷ y 4
(iii) 8(x 3 y 2 z 2 + x 2 y 3 z 2 + x 2 y 2 z 3 ) ÷ 4x 2 y 2 z 2
(iv) (x 3 + 2x 2 + 3x) ÷ 2x
(v) (p 3 q 6 – p 6 q 3 ) ÷ p 3 q 3
हल: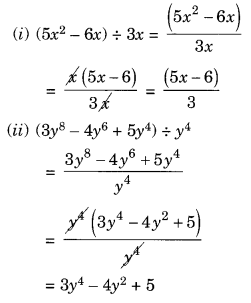
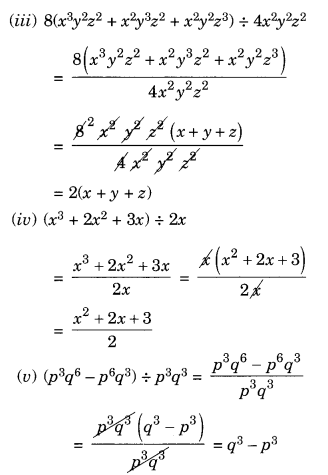
प्रश्न 3.
निम्नलिखित विभाजनों को हल करें।
(i) (10x – 25) ÷ 5
(ii) (10x – 25) ÷ (2x – 5)
(iii) 10y(6y + 21) ÷ 5(2y + 7)
(iv) 9x 2 y 2 (3z – 24) ÷ 27xy(z – 8)
(v) 96abc(3a – 12) (5b – 30) ÷ 144(a – 4)(b – 6)
हल: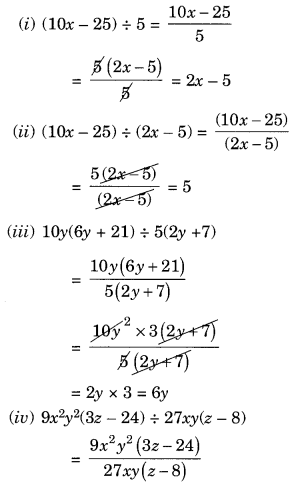
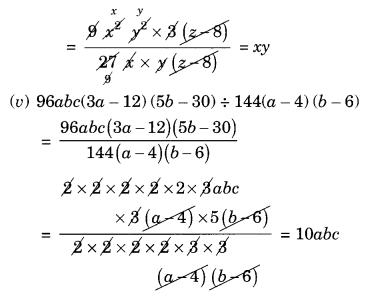
प्रश्न 4.
निर्देशानुसार विभाजित करें।
(i) 5(2x + 1) (3x + 5) ÷ (2x + 1)
(ii) 26xy (x + 5)(y – 4) ÷ 13x(y – 4)
(iii) 52pqr(p + q) (q + r) (r + p) ÷ 104pq(q + r)(r + p)
(iv) 20(y + 4)(y 2 + 5y + 3) ÷ 5(y + 4)
(v) x(x + 1) (x + 2) (x + 3) ÷ x(x + 1)
हल: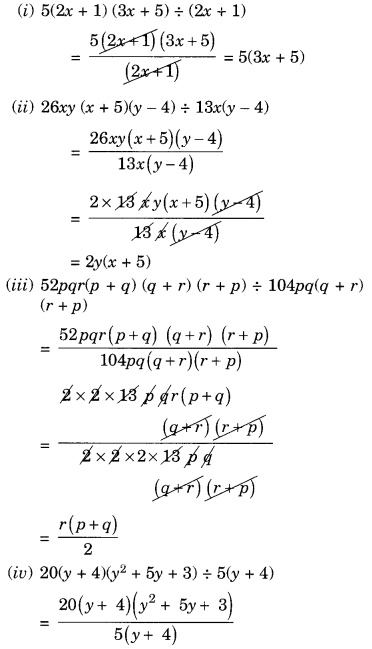
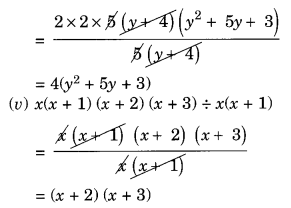
प्रश्न 5.
व्यंजकों का गुणनखंडन कीजिए और उन्हें निर्देशानुसार विभाजित कीजिए।
(i) (y 2 + 7y + 10) ÷ (y + 5)
(ii) (m 2 – 14m – 32) ÷ (m + 2)
(iii) (5p 2 – 25p + 20) ÷ (p – 1)
(iv) 4yz(z 2 + 6z – 16) ÷ 2y(z + 8)
(v) 5pq(p 2 – q 2 ) ÷ 2p(p + q)
(vi) 12xy(9x 2 – 16y 2 ) ÷ 4xy(3x + 4y)
(vii) 39y 3 (50y 2 – 98) ÷ 26y 2 (5y + 7)
हल: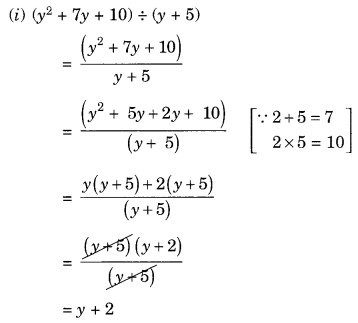
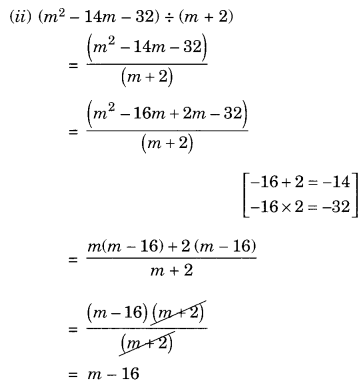
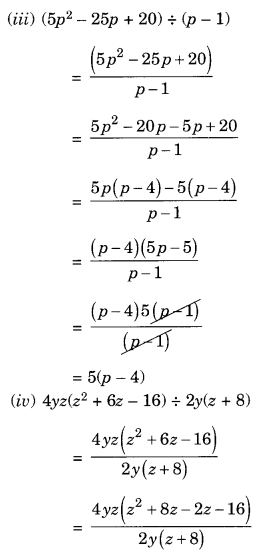
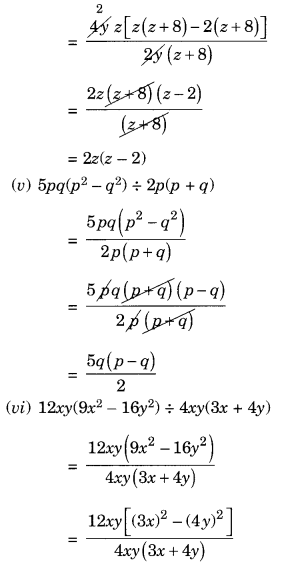
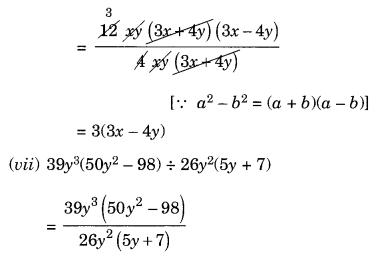
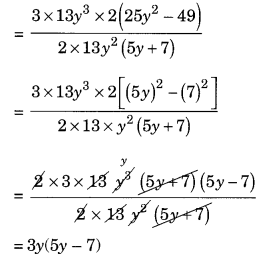
Ex 14.4
प्रश्न 1.
निम्नलिखित गणितीय कथनों में त्रुटियाँ ज्ञात कीजिए और उन्हें सही कीजिए।
उत्तर:
(1) 4(x – 5) = 4x – 5
दिया गया कथन गलत है।
सही कथन
4(x – 5) = 4x – 20 है।
(2) x (3x + 2) = 3x 2 + 2
दिया गया कथन गलत है।
सही कथन x (3x + 2) = 3x 2 + 2x है।
(3) 2x + 3y = 5xy
यह एक गलत कथन है।
सही कथन 2x + 3y = 2x + 3y है।
(4) x + 2x + 3x = 5x
यह एक गलत कथन है।
सही कथन x + 2x + 3x = 6x है।
(5) 5y + 2y + y – 7y = 0
यह एक गलत कथन है।
सही कथन है
5y + 2y + y – 7y = y
(6) 3x + 2x = 5x 2
यह एक गलत कथन है।
सही कथन 3x + 2x = 5x है।
(7) (2x) 2 + 4(2x) + 7 = 2x 2 + 8x + 7
यह दिया गया कथन गलत है।
सही कथन है
(2x) 2 + 4 (2x) + 7 = 4x 2 + 8x + 7
(8) (2x) 2 + 5x = 4x + 5x = 9x 2
दिया गया कथन गलत है।
सही कथन है (2x) 2 + 5x = 4x 2 + 5x
(9) (3x + 2) 2 = 3x 2 + 6x + 4
दिया गया कथन गलत है।
सही कथन है:
(3x + 2) 2 = (3x) 2 + 2 × 3x × 2 + (2) 2
(3x + 2) 2 = 9x 2 + 12x + 4
(10)
(a) में x = – 3 प्रतिस्थापित करने पर x 2 + 5x + 4
= (- 3) 2 + 5 (-3) + 4
= 9 + 2 + 4
= 15
दिया गया कथन गलत है।
सही कथन x 2 + 5x + 4
= (-3) 2 + 5 (- 3) + 4
= 9 – 15 + 4
= 13 – 15 = – 2 है।
∴ x = – 3 पर x 2 + 5x + 4 = -2 है।
(b) x 2 – 5x + 4
= (-3) 2 – 5 (-3) + 4
= 9 – 15 + 4 = -2
दिया गया कथन गलत है।
सही कथन
x 2 – 5x + 4
= (-3) 2 – 5 (-3) + 4
= 9 + 15 +4 = 28 है।
(c) x 2 + 5x = (-3) 2 + 5 (-3)
= – 9 – 15 = – 24
दिया गया कथन गलत है।
सही कथन
x 2 + 5x
= (-3) 2 + 5(—3)
= 9 – 15 = -6 है।
(11) (y – 3) 2 = y 2 – 9
दिया गया कथन गलत है। (y-3) 2
= y 2 – 2 (y) (3) + 3 2
= y 2 – 6y + 9
सही कथन है (y – 3) 2 = y 2 – 6y + 9
(12) (z + 5) 2 = z 2 + 25
दिया गया कथन गलत है।
(z + 5) 2 = z 2 + 2 × z × 5 + 5 2
= z 2 + 10z + 25
सही कथन है (z + 5) 2 = z 2 + 10z + 25
(13) (2a + 3b) (a – b) = 2a 2 – 3b 2
दिया गया कथन गलत है।
(2a + 3b) (a – b)
= 2a (a – b) + 3b (a – b)
= 2a 2 – 2ab + 3ab – 3b 2
= 2a 2 + ab – 3b 2
सही कथन है
(2a + 3b) (a – b) = 2a 2 + ab – 3b 2
(14) (a + 4) (a + 2) = a 2 + 8
दिया गया कथन गलत है।
(a + 4) (a + 2)
= a (a + 2) + 4 (a + 2)
= a 2 + 2a + 4a + 8
= a 2 + 6a + 8
सही कथन है (a + 4) (a + 2) = a 2 + 6a + 8
(15) (a – 4) (a – 2) = a 2 – 8
दिया गया कथन गलत है, (a – 4) (a – 2)
= a(a – 2) – 4(a – 2)
= a 2 – 2a – 4a + 8
= a 2 – 6a + 8
सही कथन है (a – 4) (a – 2) = a 2 – 6a + 8
