SikhLo - Current Affairs in Hindi, Daily current affairs, Current affairs

 NCERT Class 9 Maths Chapter 1 संख्या पद्धति

NCERT Solutions for Class 9 Maths Chapter 1 संख्या पद्धति

Ex 1.1

प्रश्न 1.
क्या शून्य एक परिमेय संख्या है? क्या आप इसे pq के रूप में लिख सकते हैं, जहाँ p और q पूर्णांक हैं और q ≠0 है?
हल:
हाँ, शून्य एक परिमेय संख्या है, इसे pq के रूप में लिखा जा सकता है।
0 = 01 = 02 = 03 आदि। हर q को ऋणात्मक पूर्णांक भी लिया जा सकता है।

प्रश्न 2.
3 और 4 के बीच छह परिमेय संख्याएँ ज्ञात कीजिए ।
हल:
मान लीजिए q i , 3
​​और 4 के बीच की परिमेय संख्या है, जहाँ j = 1 से 6 है।
∴ छह परिमेय संख्याएँ इस प्रकार हैं: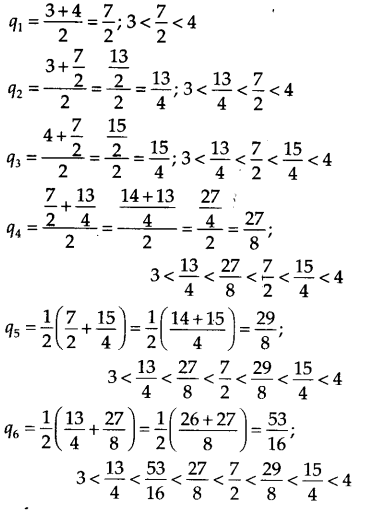

इस प्रकार, 3 और 4 के बीच की छह परिमेय संख्याएँ हैं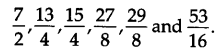

प्रश्न 3.
35 और 45 के बीच पाँच परिमेय संख्याएँ ज्ञात कीजिए।
हल:
चूँकि, हमें पाँच परिमेय संख्याएँ ज्ञात करनी हैं, इसलिए अंश और हर को 6 से गुणा कीजिए।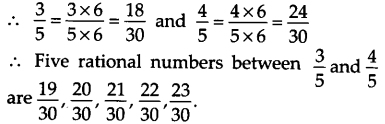

प्रश्न 4.
बताइए कि निम्नलिखित कथन सत्य हैं या असत्य। अपने उत्तरों के लिए कारण दीजिए।
(i) प्रत्येक प्राकृत संख्या एक पूर्ण संख्या होती है।
(ii) प्रत्येक पूर्णांक एक पूर्ण संख्या होती है।
(iii) प्रत्येक परिमेय संख्या एक पूर्ण संख्या होती है।
हल:
(i) सत्य
∵ सभी प्राकृत संख्याओं और 0 के समूह को पूर्ण संख्याएँ कहते हैं।
(ii) असत्य
∵ ऋणात्मक पूर्णांक पूर्ण संख्याएँ नहीं होते हैं।
(iii) असत्य
∵ परिमेय संख्याएँ p/q के रूप की होती हैं, q ≠ 0 और q, p को पूर्णतः विभाजित नहीं करता है जो पूर्ण संख्याएँ नहीं हैं।

Ex 1.2

प्रश्न 1.
बताइए कि निम्नलिखित कथन सत्य हैं या असत्य। अपने उत्तरों का औचित्य सिद्ध कीजिए।
(i) प्रत्येक अपरिमेय संख्या एक वास्तविक संख्या होती है।
(ii) संख्या रेखा पर प्रत्येक बिंदु √m के रूप का होता है, जहाँ m एक प्राकृत संख्या है।
(iii) प्रत्येक वास्तविक संख्या एक अपरिमेय संख्या होती है।
हल:
(i) सत्य
क्योंकि सभी परिमेय संख्याएँ और सभी अपरिमेय संख्याएँ वास्तविक संख्याओं का समूह (संग्रह) बनाती हैं।
(ii) असत्य
क्योंकि ऋणात्मक संख्याएँ किसी भी प्राकृत संख्या का वर्गमूल नहीं हो सकती हैं।
(iii) असत्य
क्योंकि परिमेय संख्याएँ भी वास्तविक संख्याओं का एक भाग होती हैं।

प्रश्न 2.
क्या सभी धनात्मक पूर्णांकों के वर्गमूल अपरिमेय होते हैं? यदि नहीं, तो किसी ऐसी संख्या के वर्गमूल का उदाहरण दीजिए जो एक परिमेय संख्या हो।
हल:
नहीं, यदि हम एक धनात्मक पूर्णांक, मान लीजिए 9, लेते हैं, तो उसका वर्गमूल 3 है, जो एक परिमेय संख्या है।

प्रश्न 3.
दर्शाइए कि संख्या रेखा पर √5 को किस प्रकार दर्शाया जा सकता है।
हल:
एक संख्या रेखा खींचिए और उस पर बिंदु O और A इस प्रकार लीजिए कि OA = 1 इकाई हो। BA ⊥ OA खींचिए क्योंकि BA = 1 इकाई हो। OB को मिलाइए = √2 इकाई।
अब BB 1 ⊥ OB इस प्रकार खींचिए कि BB 1 = 1 इकाई हो। OB को मिलाइए = √3 इकाई।
इसके बाद, B 1 B 2 ⊥ OB 1 इस प्रकार खींचिए कि B 1 B 2 = 1 इकाई हो। OB को
मिलाइए = इकाई। पुनः B 2 B 3 ⊥ OB 2 इस प्रकार खींचिए कि B 2 B 3 = 1 इकाई हो। OB को मिलाइए = √5 इकाई। O को केंद्र और OB 3 को त्रिज्या मानकर एक चाप खींचिए जो संख्या रेखा को D पर काटता है। बिंदु D संख्या रेखा पर √5 को दर्शाता है।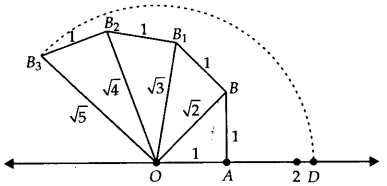

प्रश्न 4.
कागज़ की एक बड़ी शीट लें और निम्नलिखित तरीके से 'वर्गमूल सर्पिल' का निर्माण करें। बिंदु O से शुरू करें और इकाई लंबाई का एक रेखाखंड OP 1 खींचें। इकाई लंबाई का OP 1 पर लंबवत एक रेखाखंड P 1 , P 2 खींचें (आकृति देखें)। अब, OP 2 पर लंबवत एक रेखाखंड P 2 P 3 खींचें। फिर OP 3 पर लंबवत एक रेखाखंड P 3 P 4 खींचें। इस तरीके से जारी रखते हुए, आप OP n - 1 पर लंबवत इकाई लंबाई का एक रेखाखंड खींचकर रेखाखंड P n-1 P n प्राप्त कर सकते हैं । इस तरीके से, आपने बिंदु P 2 , P 3 ,…… P n ,….. बनाए होंगे और उन्हें मिलाकर √2,√3,√4,…… दर्शाने वाला एक सुंदर सर्पिल बनाया होगा ।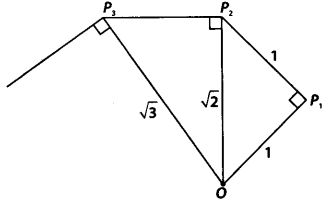

Ex 1.3

प्रश्न 1.
आप जानते हैं कि17=0.142857¯क्या आप भविष्यवाणी कर सकते हैं कि का दशमलव विस्तार क्या होगा?27,137,47,57,67क्या हैं, बिना लंबा भाग किए? अगर हाँ, तो कैसे?
हल:
हमें दिया गया है कि17=0.142857¯.
∴27= 2 x17= 2 x (0.142857¯) =0.285714¯
37= 3 x17= 3 x (0.142857¯) =0.428571¯
47= 4 x17= 4 x (0.142857¯) =0.571 428¯
57= 5 x17= 5 x(0.142857¯) =0.714285¯
67= 6 x17= 6 x (0.142857¯) =0.8571 42¯
इस प्रकार, वास्तव में दीर्घ विभाजन किए बिना ही हम दी गई परिमेय संख्याओं के दशमलव प्रसार की भविष्यवाणी कर सकते हैं।

प्रश्न 2.
निम्नलिखित को निम्न रूप में व्यक्त करेंपीक्यूजहाँ p और q पूर्णांक हैं और q ≠ 0.
(i) 0.6¯
(ii) 0.47¯
(iii) 0.001¯¯¯¯¯¯¯¯
हल:
(i) मान लीजिए x = 0.6¯= 0.6666… … (1)
चूँकि यहाँ केवल एक ही दोहराव वाला अंक है, इसलिए
(1) को दोनों तरफ 10 से गुणा करने पर, हमें
10x = 6.6666… … (2)
(1) को (2) से घटाने पर, हमें
10x – x = 6.6666… -0.6666… मिलता है
⇒ 9x = 6 ⇒ x =69=23
इस प्रकार, 0.6¯=23

(ii) मान लीजिए x = 0.47¯= 0.4777… … (1)
चूँकि यहाँ केवल एक ही दोहराव वाला अंक है, दोनों तरफ (1) को lo से गुणा करने पर, हमें
10x = 4.777 प्राप्त होता है
(1) को (2) से घटाने पर, हमें
10x – x = 4.777…… – 0.4777…… प्राप्त होता है।
⇒ 9x = 4.3 ⇒ x =4390
इस प्रकार, 0.47¯=4390

(iii) मान लीजिए x = 0.001¯¯¯¯¯¯¯¯= 0.001001… … (1)
चूँकि दोनों तरफ 3 दोहराए गए अंक हैं,
(1) को दोनों तरफ 1000 से गुणा करने पर, हमें
1000x = 1.001001 मिलता है… (2)
(1) को (2) से घटाने पर, हमें
1000x – x = (1.001…) – (0.001…) मिलता है
⇒ 999x = 1 ⇒ x =1999
इस प्रकार, 0.001¯¯¯¯¯¯¯¯=1999

प्रश्न 3.
0.99999… को इस रूप में व्यक्त करेंपीक्यूक्या आप अपने उत्तर से हैरान हैं? अपने शिक्षक और सहपाठियों के साथ चर्चा करें कि यह उत्तर क्यों उचित है।
हल:
मान लीजिए x = 0.99999….. …. (i)
चूँकि केवल एक ही दोहराव वाला अंक है, इसलिए
(i) को दोनों ओर 10 से गुणा करने पर, हमें
10x = 9.9999 प्राप्त होता है… (ii)
(i) को (ii) से घटाने पर, हमें
10x – x = (99999 ) — (0.9999 )
⇒ 9x = 9 ⇒ x =99= 1
इस प्रकार, 0.9999 =1
चूंकि 0.9999... हमेशा चलता रहता है, इसलिए 1 और 0.9999 के बीच इतना बड़ा अंतर नहीं है
इसलिए, दोनों बराबर हैं।

प्रश्न 4.
दशमलव प्रसार में अंकों के आवर्ती ब्लॉक में अंकों की अधिकतम संख्या कितनी हो सकती है?117अपने उत्तर की जाँच के लिए भाग कीजिए। हल
:
117, भाजक में 17 है।
चूंकि, अंकों के दोहराए जाने वाले ब्लॉक में प्रविष्टियों की संख्या भाजक से कम है, तो दोहराए जाने वाले ब्लॉक में अंकों की अधिकतम संख्या 16 है।
1 को 17 से विभाजित करने पर, हमें

शेष I मिलता है जो वही अंक है जिससे हमने विभाजन शुरू किया था।
∴117= 0.0588235294117647¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
इस प्रकार, दशमलव विस्तार में दोहराए जाने वाले ब्लॉक में 16 अंक हैं117अतः
हमारा उत्तर सत्यापित है।

प्रश्न 5.
परिमेय संख्याओं के कई उदाहरण देखेंपीक्यू(q ≠ 0)। जहाँ, p और q पूर्णांक हैं जिनमें 1 के अलावा कोई उभयनिष्ठ गुणनखंड नहीं है और उनके सांत दशमलव निरूपण (प्रसार) हैं। क्या आप अनुमान लगा सकते हैं कि q को किस गुणधर्म की पूर्ति करनी चाहिए?
हल:
आइए निम्नलिखित सांत परिमेय संख्याओं के दशमलव प्रसार पर विचार करें:


हम देखते हैं कि q के अभाज्य गुणनखंडन (अर्थात हर) में केवल 2 की घातें या 5 की घातें या दोनों की घातें होती हैं।

प्रश्न 6.
तीन संख्याएँ लिखिए जिनके दशमलव प्रसार अनवसानी अनावर्ती हैं।
हल:
√2 = 1.414213562 ………..
√3 = 1.732050808 …….
√5 = 2.23606797 …….

प्रश्न 7.
परिमेय संख्याओं के बीच तीन भिन्न अपरिमेय संख्याएँ ज्ञात कीजिए57और911
हल: हमारे
पास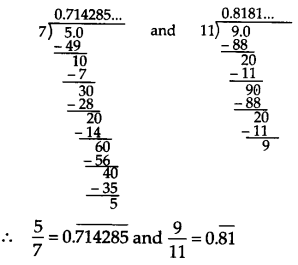

0 के बीच तीन अपरिमेय संख्याएँ हैं।714285¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯और 0.81¯¯¯¯¯हैं
(i) 0.750750075000 …..
(ii) 0.767076700767000 ……
(iii) 0.78080078008000 ……

प्रश्न 8.
निम्नलिखित संख्याओं को परिमेय या अपरिमेय के रूप में वर्गीकृत करें
(i)225−−−√
(ii) 0.3796
(iii) 7.478478…..
(iv) 1.101001000100001………
हल:
(i) ∵ 225 = 15 x 15 = 15 2
∴ 225 एक पूर्ण वर्ग संख्या है।
अत:225−−−√एक परिमेय संख्या है।
(ii) ∵ 0.3796 एक सांत दशमलव है।
∴ यह एक परिमेय संख्या है।
(iii) 7.478478… = 7.478¯¯¯¯¯¯¯¯
चूंकि, 7.478¯¯¯¯¯¯¯¯एक अनवसानी आवर्ती (दोहरावदार) दशमलव है।
∴ यह एक परिमेय संख्या है।
(iv) चूँकि, 1.101001000100001… एक अनवसानी, अनवरती दशमलव संख्या है।
∴ यह एक अपरिमेय संख्या है।

Ex 1.4

प्रश्न 1.
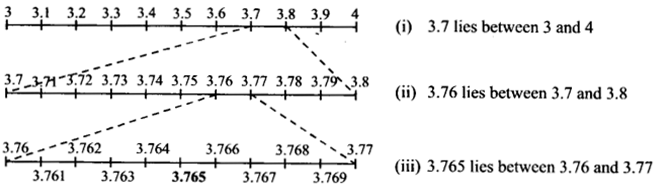
क्रमिक आवर्धन का उपयोग करके, संख्या रेखा पर 3.765 को दर्शाइए।
हल:
3.765, 3 और 4 के बीच स्थित है।

प्रश्न 2.
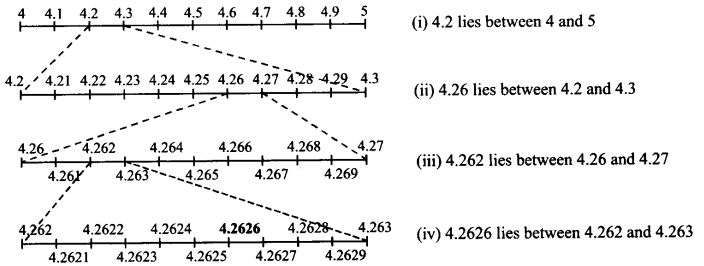
कल्पना कीजिए 4.26¯संख्या रेखा पर, 4 दशमलव स्थानों तक।
हल:
4.26¯या 4.2626, 4 और 5 के बीच स्थित है।

Ex 1.5

प्रश्न 1.
निम्नलिखित संख्याओं को परिमेय और अपरिमेय के रूप में वर्गीकृत करें।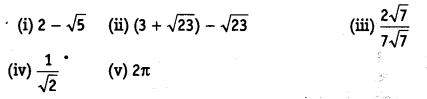

हल:
(i) चूँकि यह एक परिमेय और एक अपरिमेय संख्या का अंतर है। ∴ 2 – √5 एक अपरिमेय संख्या है। (ii) 3 + √5
एक अपरिमेय संख्या है।
23−−√–23−−√= 3 +23−−√–23−−√= 3
जो एक परिमेय संख्या है।
(iii) चूँकि,27√77√=2 ×7√7 ×7√=27, जो एक परिमेय संख्या है।
(iv) ∵ परिमेय और अपरिमेय संख्या का भागफल एक अपरिमेय संख्या होती है
।12√एक अपरिमेय संख्या है।
(v) ∵ 2π = 2 x π = एक परिमेय और एक अपरिमेय संख्या का गुणनफल एक अपरिमेय संख्या होती है।
∴ 2π एक अपरिमेय संख्या है।

प्रश्न 2.
निम्नलिखित प्रत्येक व्यंजक को सरल कीजिए

। हल:
(i) (3 + √3)(2 + √2)
= 2(3 + √3) + √2(3 + √3)
= 6 + 2√3 + 3√2 + √6
इस प्रकार, (3 + √3)(2 + √2) = 6 + 2√3 + 3√2 + √6
(ii) (3 + √3)(3 – √3) = (3) 2 – (√3) 2
= 9 – 3 = 6
इस प्रकार, (3 + √3)(3 – √3) = 6
(iii) (√5 + √2) 2 = (√5) 2 + (√2) 2 + 2(√5)(√2)
= 5 + 2 + 2√10 = 7 + 2√10
इस प्रकार, (√5 + √2) 2 = 7 + 2√10
(iv) (√5 – √2)(√5 + √2) = (√5) 2 – (√2) 2 = 5 – 2 = 3
इस प्रकार, (√5 – √2) (√5 + √2) = 3

प्रश्न 3.
याद कीजिए, π को एक वृत्त की परिधि (मान लीजिए c) और उसके व्यास (मान लीजिए d) के अनुपात के रूप में परिभाषित किया जाता है। अर्थात् π =सीडीयह इस तथ्य का खंडन करता प्रतीत होता है कि n अपरिमेय है। आप इस विरोधाभास का समाधान कैसे करेंगे?
हल:
जब हम किसी रेखा की लंबाई को पैमाने या किसी अन्य उपकरण से मापते हैं, तो हमें केवल एक अनुमानित परिमेय मान प्राप्त होता है, अर्थात c और d दोनों अपरिमेय हैं।
∴सीडीअपरिमेय है और इसलिए π अपरिमेय है।
इस प्रकार, यह कहने में कोई विरोधाभास नहीं है कि यह अपरिमेय है।

प्रश्न 4.
निरूपित करें9.3−−−√संख्या रेखा पर।
हल:
AB = 9.3 इकाई का एक रेखाखंड खींचिए और इसे C तक इस प्रकार बढ़ाइए कि BC = 1 इकाई हो।
AC का मध्य बिंदु ज्ञात कीजिए और उसे O से चिह्नित कीजिए।
O को केंद्र और AO को त्रिज्या मानकर एक अर्धवृत्त खींचिए। BD ⊥ AC खींचिए।
B को केंद्र और BD को त्रिज्या मानकर एक चाप खींचिए जो बढ़ाए गए AC को E पर इस प्रकार मिले कि BE = BD =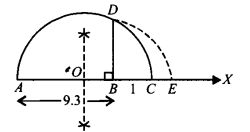9.3−−−√इकाइयाँ.

Ex 1.6

प्रश्न 1.
ज्ञात कीजिए:

हल:
(i) 64 = 8 x 8 = 8 2
∴ (64) 1/2 = (82) 1/2 = 8 2 x 1/2 = 8 [(a m ) n = a m xn ]
(ii) 32 = 2 x 2x 2 x 2 x 2 = 2 5
∴ (32) 1/5 = (2 5 ) 1/5 = 2 5 x 1/5 = 2 [(a m ) n = a m xn ]
(iii) 125 = 5 x 5 x 5 = 5 3
∴ (125) 1/3 = (5 3 ) 1/3 = 5 3 x 1/3 = 5 [(a m ) n = a m xn ]

प्रश्न 2.
ज्ञात कीजिए:

हल:
(i) 9 = 3 x 3 = 3 2
∴ (9) 3/2 = (3 2 ) 3/2 = 3 2 x 3/2 = 3 3 = 27
[(a m ) n = a mn ]
(ii) 32 = 2 x 2 x 2 x 2 x 2= 2 5
∴ (32) 2/5 = (2 5 ) 2/5 = 2 5 x 2/5 = 2 2 = 4
[(a m ) n = a mn ]
(iii) 16 = 2 x 2 x 2 x 2 = 2 4
∴ (16) 3/4 = (2 4 ) 3/4 = 2 4 x 3/4 = 2 3 = 8
[(a m ) n = a mn ]
(iv) 125 = 5 x 5 x 5 = 53
∴ (125) -1/3 = (5 3 ) -1/3 = 5 3 x (-1/3) = 5 -1
=15[ एक   1एएन]

प्रश्न 3.
सरल करें: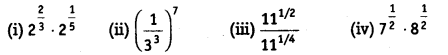

हल:
(i) 2 2/3 . 2 1/5 = 2 2/3 + 1/5 = 2 13/15
[a m . a n = a m + n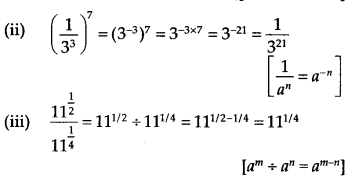

(iv) 7 1/2 .8 1/2 = (7 x 8) 1/2 = (56) 1/2 [a m x b m = (ab) m ]