SikhLo - Current Affairs in Hindi, Daily current affairs, Current affairs

 NCERT Class 9 Maths Chapter 2 बहुपद

NCERT Solutions for Class 9 Maths Chapter 2 बहुपद

Ex 2.1

प्रश्न 1.
निम्नलिखित में से कौन से व्यंजक एक चर वाले बहुपद हैं और कौन से नहीं हैं? अपने उत्तर के लिए कारण बताइए।
(i) 4x 2 – 3x + 7
(ii) y 2 + √2
(iii) 3 √t + t√2
(iv) x 10 + y 3 +t 50
हल:
(i) हमारे पास है 4x 2 – 3x + 7 = 4x 2 – 3x + 7x 0
यह एक चर अर्थात x में एक बहुपद है
क्योंकि x का प्रत्येक घातांक एक पूर्ण संख्या है।

(ii) हमारे पास y 2 + √2 = y 2 + √2y 0
है । यह एक चर अर्थात् y वाला बहुपद है,
क्योंकि y का प्रत्येक घातांक एक पूर्ण संख्या है।

(iii) हमारे पास है 3 √t + t√2 = 3 √t 1/2 + √2.t
यह एक बहुपद नहीं है, क्योंकि t का एक घातांक \(\frac { 1 }{ 2 }\) है,12,
जो पूर्ण संख्या नहीं है।

(iv) यहाँ, प्रत्येक चर का घातांक एक पूर्ण संख्या है, लेकिन x 10 + y 3 +  t 50 , x , y और t, अर्थात् तीन चरों में एक बहुपद है। अतः, यह एक चर वाला बहुपद नहीं है।

प्रश्न 2.
घात 35 वाले द्विपद और घात 100 वाले एकपदी का एक-एक उदाहरण दीजिए।
हल:
(i) घात 35 वाला द्विपद 3x 35 -4 हो सकता है। (ii) घात 100 वाला एकपदी √2y 100
हो सकता है ।

प्रश्न 3.
निम्नलिखित बहुपदों में से प्रत्येक की घात लिखिए।
(i) 5x 3 + 4x 2 + 7x
(ii) 4 – y 2
(iii) 5t – √7
(iv) 3
हल:
(i) दिया गया बहुपद 5x 3 + 4x 2 + 7x है।
चर x की उच्चतम घात 3 है।
इसलिए, बहुपद की घात 3 है।
(ii) दिया गया बहुपद 4- y 2
है। चर y की उच्चतम घात 2 है
। इसलिए, बहुपद की घात 2 है।
(iii) दिया गया बहुपद 5t – √7 है। चर t की उच्चतम घात 1 है। इसलिए, बहुपद की घात 1 है।
(iv) चूँकि, 3 = 3x° [∵ x°=1]
इसलिए, बहुपद की घात 0 है।

प्रश्न 4.
निम्नलिखित को रैखिक, द्विघाती और त्रिघाती बहुपदों के रूप में वर्गीकृत करें।
(i) x 2 + x
(ii) x – x 3
(iii) y + y 2 +4
(iv) 1 + x
(v) 3t
(vi) r 2
(vii) 7x 3
हल: (i) x 2
+ x की घात 2 है। इसलिए, यह एक द्विघाती बहुपद है। (ii) x – x 3 की घात 3 है। इसलिए, यह एक त्रिघाती बहुपद है।

(iii) y + y 2 + 4 की घात 2 है। अतः यह एक द्विघात बहुपद है।

(iv) 1 + x की घात 1 है। अतः यह एक रैखिक बहुपद है।
(v) 3t की घात 1 है। अतः यह एक रैखिक बहुपद है। (vi) r 2
की घात 2 है। अतः यह एक द्विघात बहुपद है। (vii) 7x 3 की घात 3 है। अतः यह एक त्रिघात बहुपद है।

Ex 2.2

प्रश्न 1.
बहुपद 5x – 4x 2 + 3 का मान ज्ञात कीजिए,
(i) x = 0
(ii) x = – 1
(iii) x = 2
हल:
1et p(x) = 5x – 4x 2 + 3
(i) p(0) = 5(0) – 4(0) 2 + 3 = 0 – 0 + 3 = 3 इस प्रकार, x = 0 पर 5x – 4x 2
+ 3 का मान 3 है। (ii) p(-1) = 5(-1) – 4(-1) 2 + 3 = – 5x – 4x 2 + 3 = -9 + 3 = -6 इस प्रकार, x = -1 पर 5x – 4x 2 + 3 का मान -6 है। (iii) p(2) = 5(2) – 4(2) 2 + 3 = 10 – 4(4) + 3 = 10 – 16 + 3 = -3 इस प्रकार, x = 2 पर 5x – 4x 2 + 3 का मान – 3 है।

प्रश्न 2.
निम्नलिखित बहुपदों में से प्रत्येक के लिए p (0), p (1) और p (2) ज्ञात कीजिए।
(i) p(y) = y 2 – y +1
(ii) p (t) = 2 +1 + 2t 2 -t 3
(iii) P (x) = x 3
(iv) p (x) = (x-1) (x+1)
हल:
(i) दिया गया है कि p(y) = y 2 – y + 1.
∴ P(0) = (0) 2 – 0 + 1 = 0 – 0 + 1 = 1
p(1) = (1) 2 – 1 + 1 = 1 – 1 + 1 = 1
p(2) = (2) 2 – 2 + 1 = 4 – 2 + 1 = 3
(ii) दिया गया है कि p(t) = 2 + t + 2t 2 – t 3
∴p(0) = 2 + 0 + 2(0) 2 – (0) 3
= 2 + 0 + 0 – 0=2
P(1) = 2 + 1 + 2(1) 2 – (1) 3
= 2 + 1 + 2 – 1 = 4
p( 2) = 2 + 2 + 2(2) 2 – (2) 3
= 2 + 2 + 8 – 8 = 4
(iii) दिया है कि p(x) = x 3
∴ p(0) = (0) 3 = 0, p(1) = (1) 3 = 1
p(2) = (2) 3 = 8
(iv) दिया है कि p(x) = (x – 1)(x + 1)
∴ p(0) = (0 – 1)(0 + 1) = (-1)(1) = -1
p(1) = (1 – 1)(1 +1) = (0)(2) = 0
P(2) = (2 – 1)(2 + 1) = (1)(3) = 3

प्रश्न 3.
सत्यापित कीजिए कि क्या निम्नलिखित उनके सामने दिए गए बहुपद के शून्यक हैं।
(i) p(x) = 3x + 1,x = – \frac { 1 }{ 3 }13
(ii) पी (x) = 5x – π, x =45
(iii) p (x) = x 2 – 1, x = x – 1
(iv) p (x) = (x + 1) (x – 2), x = – 1,2
(v) p (x) = x 2 , x = 0
(vi) p (x) = 1x + m, x = – m1
(vii) P (x) = 3x2 – 1, x = – 13√,23√
हल:

(i) हमारे पास है, p(x) = 3x + 1

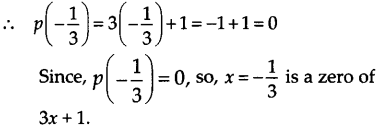
(ii) हमारे पास है, p(x) = 5x – π
∴p ( −13)=3 ( −13)+1=− 1+1=0
(iii) हमारे पास है, p(x) = x 2 – 1
∴ p(1) = (1) 2 – 1 = 1 – 1=0 चूँकि, p(1) = 0, इसलिए x = 1, x 2 -1
का शून्यक है । साथ ही, p(-1) = (-1) 2 -1 = 1 – 1 = 0 चूँकि p(-1) = 0, इसलिए, x = -1, भी x 2 – 1 का शून्यक है ।

(iv) हमारे पास है, p(x) = (x + 1)(x – 2)
∴ p(-1) = (-1 +1) (-1 – 2) = (0)(- 3) = 0
चूँकि, p(-1) = 0, इसलिए, x = -1, (x + 1)(x – 2) का शून्यक है।
साथ ही, p( 2) = (2 + 1)(2 – 2) = (3)(0) = 0
चूँकि, p(2) = 0, इसलिए, x = 2 भी (x + 1)(x – 2) का शून्यक है।

(v) हमारे पास है, p(x) = x 2
∴ p(o) = (0) 2 = 0 चूँकि, p(0) = 0, इसलिए, x = 0, x 2
का शून्यक है ।

(vi) हमारे पास है, p(x) = lx + m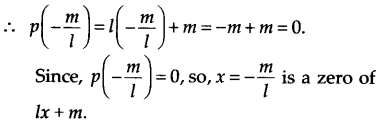

(vii) हमारे पास है, p(x) = 3x 2 – 1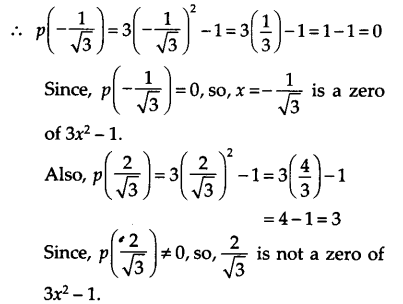

प्रश्न 4.
निम्नलिखित प्रत्येक स्थिति में बहुपद का शून्यक ज्ञात कीजिए:
(i) p(x)=x+5
(ii) p (x) = x – 5
(iii) p (x) = 2x + 5
(iv) p (x) = 3x – 2
(v) p (x) = 3x
(vi) p (x)= ax, a≠0
हल:
(i) हमारे पास है, p(x) = x + 5. चूँकि, p(x) = 0
⇒ x + 5 = 0
⇒ x = -5.
इस प्रकार, x + 5 का शून्यक -5 है।

(ii) हमारे पास है, p(x) = x – 5.
चूँकि, p(x) = 0 ⇒ x – 5 = 0 ⇒ x = -5
इस प्रकार, x – 5 का शून्य 5 है।

(iii) हमारे पास है, p(x) = 2x + 5. चूँकि, p(x) = 0
⇒ 2x + 5 = 0
⇒ 2x = -5
⇒ x = \frac { -5 }{ 2 }− 52
इस प्रकार, 2x + 5 का शून्य है− 52.

(iv) हमारे पास है, p(x) = 3x – 2. चूँकि, p(x) = 0
⇒ 3x – 2 = 0
⇒ 3x = 2
⇒ x = \frac { 2 }{ 3 }23
इस प्रकार, 3x – 2 का शून्य है23

(v) p(x) = 3x. चूँकि p(x) = 0
⇒ 3x = 0 ⇒ x = 0
अतः 3x का शून्यक 0 है।

(vi) हमारे पास है, p(x) = ax, a ≠ 0.
चूँकि, p(x) = 0 => ax = 0 => x-0
इस प्रकार, ax का शून्य 0 है।

Ex 2.3

प्रश्न 1. x 3  + 3x 2  + 3x + 1 को शेष भाग दें पर शेषफल ज्ञात करें: 
(i) x + 1 
(ii) x – \(\frac { 1 }{ 2 }\) 12
(iii) x 
(iv) x + θ
हल:
मान लीजिए p(x) = x 3 + 3x 2 + 3x +1
(i) x + 1 का शून्यक -1 है।
∴ p(-1) = (-1)3 + 3(-1)2 + 3(-1) +1
= -1 + 3- 3 + 1 = 0
अत: अभीष्ट शेष = 0

(ii) \(x-\frac { 1 }{ 2 }\) का शून्यक \(\frac { 1 }{ 2 }\) है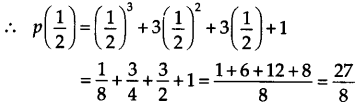 x−12है12

इस प्रकार, अभीष्ट शेष = \(\frac { 27 }{ 8 }\)278

(iii) x का शून्यक 0 है।
∴ p(0) = (0) 3 + 3(0) 2 + 3(0) + 1
= 0 + 0 + 0 + 1 = 1
अत: अभीष्ट शेषफल = 1.

(iv) x + π का ​​शून्यांक -π है।
p(-π) = (-π) 3 + 3(- π) 2 2 + 3(- π) +1
= -π 3 + 3π 2 + (-3π) + 1
= – π 3 + 3π 2 – 3π +1
इस प्रकार, आवश्यक शेषफल -π 3 + 3π 2 – 3π+1 है।

Ex 2.4

प्रश्न 1.
निर्धारित करें कि निम्नलिखित में से किस बहुपद का (x +1) एक कारक है।
(i) x 3 + x 2 + x +1
(ii) x 4 + x 3 + x 2 + x + 1
(iii) x 4 + 3x 3 + 3x 2 + x + 1
(iv) x 3 – x 2 – (2 +√2) x + √2
समाधान:
x + 1 का शून्य -1 है।
(i) माना p (x) = x 3 + x 2 + x + 1
∴ p (-1) = (-1) 3 + (-1) 2 + (-1) + 1 .
= -1 + 1 – 1 + 1
⇒ p (- 1) = 0 इसलिए, (x + 1) x 3 + x 2 + x + 1
का एक कारक है ।

(ii) मान लीजिए p (x) = x 4 + x 3 + x 2 + x + 1
∴ P(-1) = (-1) 4 + (-1) 3 + (-1) 2 + (-1)+1
= 1 – 1 + 1 – 1 + 1
⇒ P (-1) ≠ 1 अतः, (x + 1) x 4 + x 3 + x 2 + x+ 1
का गुणनखंड नहीं है ।

(iii) माना p (x) = x 4 + 3x 3 + 3x 2 + x + 1 ।
∴ p (-1)= (-1) 4 + 3 (-1) 3 + 3 (-1) 2 + (- 1) + 1
= 1 – 3 + 3 – 1 + 1 = 1
⇒ p (-1) ≠ 0 अतः, (x + 1) x 4 + 3x 3 + 3x 2 + x+ 1
का गुणनखंड नहीं है ।

(iv) माना p (x) = x 3 – x 2 – (2 + √2) x + √2
∴ p (- 1) = (- 1)3- (-1)2 – (2 + √2)(-1) + √2
= -1 – 1 + 2 + √2 + √2
= 2√2
⇒ p (-1) ≠ 0 इसलिए, (x + 1) x 3 – x 2 – (2 + √2) x + √2
का गुणनखंड नहीं है ।

प्रश्न 2.
गुणनखंड प्रमेय का उपयोग करके निर्धारित करें कि क्या निम्नलिखित प्रत्येक स्थिति में g (x) p (x) का एक गुणनखंड है
(i) p (x)= 2x 3 + x 2 – 2x – 1, g (x) = x + 1
(ii) p(x)= x 3 + 3x 2 + 3x + 1, g (x) = x + 2
(iii) p (x) = x 3 – 4x 2 + x + 6, g (x) = x – 3
हल:
(i) हमारे पास है, p (x)= 2x 3 + x 2 – 2x – 1 और g (x) = x + 1
∴ p(-1) = 2(-1) 3 + ( -1) 2 – 2(-1) – 1
= 2(-1) + 1 + 2 – 1
= -2 + 1 + 2 -1 = 0
⇒ p(-1) = 0, इसलिए g(x) p(x) का एक गुणनखंड है।

(ii) हमारे पास है, p(x) x 3 + 3x 2 + 3x + 1 और g(x) = x + 2
∴ p(-2) = (-2) 3 + 3(-2) 2 + 3(-2) + 1
= -8 + 12 – 6 + 1
= -14 + 13
= -1
⇒ p(-2) ≠ 0, इसलिए g(x) p(x) का एक कारक नहीं है।

(iii) हमारे पास है, = x 3 – 4x 2 + x + 6 और g (x) = x – 3
∴ p(3) = (3) 3 – 4(3) 2 + 3 + 6
= 27 – 4(9) + 3 + 6
= 27 – 36 + 3 + 6 = 0
⇒ p(3) = 0, इसलिए g(x) p(x) का एक कारक है।

प्रश्न 3.
k का मान ज्ञात कीजिए, यदि x – 1 निम्नलिखित प्रत्येक स्थिति में p (x) का एक गुणनखंड है
(i) p (x) = x 2 + x + k
(ii) p (x) = 2x 2 + kx + √2
(iii) p (x) = kx 2 – √2 x + 1
(iv) p (x) = kx 2 – 3x + k
हल:
(x – 1) के p(x) का एक गुणनखंड होने के लिए, p(1) 0 के बराबर होना चाहिए।

(i) यहाँ, p(x) = x 2 + x + k
चूँकि, p(1) = (1) 2 +1 + k
⇒ p(1) = k + 2 = 0
⇒ k = -2.

(ii) यहाँ, p (x) = 2x 2 + kx + √2
चूँकि, p(1) = 2(1) 2 + k(1) + √2
= 2 + k + √2 =0
k = -2 – √2 = -(2 + √2)

(iii) यहाँ, p (x) = kx 2 – √2 x + 1
चूँकि, p(1) = k(1) 2 – (1) + 1
= k – √2 + 1 = 0
⇒ k = √2 -1

(iv) यहाँ, p(x) = kx 2 – 3x + k
p(1) = k(1) 2 – 3(1) + k
= k – 3 + k
= 2k – 3 = 0
⇒ k =34

प्रश्न 4.
गुणनखंड कीजिए
(i) 12x 2 – 7x +1
(ii) 2x 2 + 7x + 3
(iii) 6x 2 + 5x – 6
(iv) 3x 2 – x – 4
हल:
(i) हमारे पास है,
12x 2 – 7x + 1 = 12x 2 – 4x- 3x + 1
= 4x (3x – 1 ) -1 (3x – 1)
= (3x -1) (4x -1)
इस प्रकार, 12x 2 -7x + 3 = (2x – 1) (x + 3)

(ii) हमारे पास है, 2x 2 + 7x + 3 = 2x 2 + x + 6x + 3
= x(2x + 1) + 3(2x + 1)
= (2x + 1)(x + 3)
इस प्रकार, 2×2 + 7x + 3 = (2x + 1)(x + 3)

(iii) हमारे पास है, 6x 2 + 5x – 6 = 6x 2 + 9x – 4x – 6
= 3x(2x + 3) – 2(2x + 3)
= (2x + 3)(3x – 2)
इस प्रकार, 6x 2 + 5x – 6 = (2x + 3)(3x – 2)

(iv) हमारे पास है, 3x 2 – x – 4 = 3x 2 – 4x + 3x – 4
= x(3x – 4) + 1(3x – 4) = (3x – 4)(x + 1)
इस प्रकार, 3x 2 – x – 4 = (3x – 4)(x + 1)

प्रश्न 5.
गुणनखंड करें
(i) x 3 – 2x 2 – x + 2
(ii) x 3 – 3x 2 – 9x – 5
(iii) x 3 + 13x 2 + 32x + 20
(iv) 2y 3 + y 2 – 2y – 1
हल:
(i) हमारे पास है, x 3 – 2x 2 – x + 2
पदों को पुनर्व्यवस्थित करने पर, हमारे पास है x 3 – x – 2x 2 + 2
= x(x 2 – 1) – 2(x 2 -1) = (x 2 – 1)(x – 2)
= [(x) 2 – (1) 2 ](x – 2)
= (x – 1)(x + 1)(x – 2)
[∵ (a 2 – b 2 ) = (a + b)(ab)]
इस प्रकार, x 3 – 2x 2 – x + 2 = (x – 1)(x + 1)(x – 2)

(ii) हमारे पास है, x 3 – 3x 2 – 9x – 5
= x 3 + x 2 – 4x 2 – 4x – 5x – 5 ,
= x 2 (x + 1) – 4x(x + 1) – 5(x + 1)
= (x + 1)(x 2 – 4x – 5)
= (x + 1)(x 2 – 5x + x – 5)
= (x + 1)[x(x – 5) + 1(x – 5)]
= (x + 1)(x – 5)(x + 1)
इस प्रकार, x 3 – 3x 2 – 9x – 5 = (x + 1)(x – 5)(x +1)

(iii) हमारे पास है, x 3 + 13x 2 + 32x + 20
= x 3 + x 2 + 12x 2 + 12x + 20x + 20
= x 2 (x + 1) + 12x(x +1) + 20(x + 1)
= (x + 1)(x 2 + 12x + 20)
= (x + 1)(x 2 + 2x + 10x + 20)
= (x + 1)[x(x + 2) + 10(x + 2)]
= (x + 1)(x + 2)(x + 10)
इस प्रकार, x 3 + 13x 2 + 32x + 20
= (x + 1)(x + 2)(x + 10)

(iv) हमारे पास है, 2y 3 + y 2 – 2y – 1
= 2y 3 – 2y 2 + 3y 2 – 3y + y – 1
= 2y 2 (y – 1) + 3y(y – 1) + 1(y – 1)
= (y – 1)(2y 2 + 3y + 1)
= (y – 1)(2y 2 + 2y + y + 1)
= (y – 1)[2y(y + 1) + 1(y + 1)]
= (y – 1)(y + 1)(2y + 1)
इस प्रकार, 2y 3 + y 2 – 2y – 1
= (y – 1)(y + 1)(2y +1)

Ex 2.5

प्रश्न 1.
निम्नलिखित गुणनफल ज्ञात करने के लिए उपयुक्त सर्वसमिकाओं का प्रयोग कीजिए
(i) (x + 4)(x + 10)
(ii) (x+8) (x -10)
(iii) (3x + 4) (3x – 5)
(iv) (y 2 +32) (y 2 –32)
(v) (3 – 2x) (3 + 2x)
हल:
(i) हमें मिलता है, (x+ 4) (x + 10)
सर्वसमिका का उपयोग करते हुए,
(x+ a) (x+ b) = x 2 + (a + b) x+ ab.
हमें मिलता है, (x + 4) (x + 10) = x 2 +(4 + 10) x + (4 x 10)
= x 2 + 14x+40

(ii) हमें मिलता है, (x+ 8) (x -10)
सर्वसमिका का उपयोग करते हुए,
(x + a) (x + b) = x 2 + (a + b) x + ab
हमें मिलता है, (x + 8) (x – 10) = x 2 + [8 + (-10)] x + (8) (- 10)
= x 2 – 2x – 80

(iii) हमें मिलता है, (3x + 4) (3x – 5)
सर्वसमिका का उपयोग करते हुए,
(x + a) (x + b) = x 2 + (a + b) x + ab
हमें मिलता है, (3x + 4) (3x – 5) = (3x) 2 + (4 – 5) x + (4) (- 5)
= 9x 2 – x – 20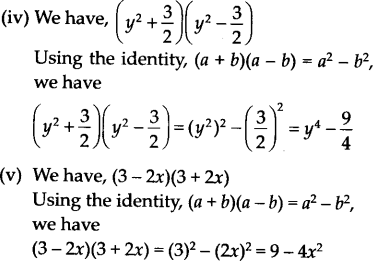

प्रश्न 2.
सीधे गुणा किए बिना निम्नलिखित उत्पादों का मूल्यांकन करें
(i) 103 x 107
(ii) 95 x 96
(iii) 104 x 96
समाधान:
(i) हमारे पास है, 103 x 107 = (100 + 3) (100 + 7)
= (100) 2 + (3 + 7) (100) + (3 x 7)
[(x + a)(x + b) = x 2 + (a + b)x + ab का उपयोग करके]
= 10000 + (10) x 100 + 21
= 10000 + 1000 + 21=11021

(ii) हमारे पास है, 95 x 96 = (100 – 5) (100 – 4)
= ( 100) 2 + [(- 5) + (- 4)] 100 + (- 5 x – 4)
[(x + a)(x + b) = x 2 + (a + b)x + ab का उपयोग करते हुए]
= 10000 + (-9) + 20 = 9120
= 10000 + (-900) + 20 = 9120

(iii) हमारे पास है 104 x 96 = (100 + 4) (100 – 4)
= (100) 2 -4 2
[(a + b)(a -b) = a 2 – b 2 का उपयोग करते हुए ]
= 10000 – 16 = 9984

प्रश्न 3.
उपयुक्त सर्वसमिकाओं का प्रयोग करके निम्नलिखित के गुणनखंड कीजिए
(i) 9x 2  + 6xy + y 2
(ii) 4y 2 -4y + 1
(iii) x 2 –य2100
हल:
(i) हमारे पास है, 9x 2 + 6xy + y 2
= (3x) 2 + 2(3x)(y) + (y) 2
= (3x + y) 2 [a 2 + 2ab + b 2 = (a + b) 2
का उपयोग करके ] = (3x + y)(3x + y)

(ii) हमारे पास है, 4y 2 – 4y + 1 2
= (2y) 2 + 2(2y)(1) + (1) 2
= (2y -1) 2 [a 2 – 2ab + b 2 = (a- b) 2
का उपयोग करते हुए ] = (2y – 1)(2y – 1 )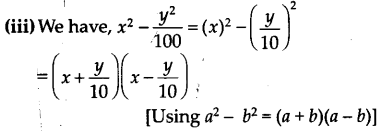

प्रश्न 4.
उपयुक्त सर्वसमिका का प्रयोग करते हुए निम्नलिखित में से प्रत्येक का विस्तार कीजिए:
(i) (x+2y+ 4z) 2
(ii) (2x – y + z) 2
(iii) (- 2x + 3y + 2z) 2
(iv) (3a -7b – c) z
(v) (- 2x + 5y – 3z) 2
(vi) [14ए -14b + 1] 2
हल:
हम जानते हैं कि
(x + y + z) 2 = x 2 + y 2 + z 2 + 2xy + 2yz + 2zx

(i) (x + 2y + 4z) 2
= x 2 + (2y ) 2 + (4z) 2 + 2 (x) (2y) + 2 (2y) (4z) + 2(4z) (x)
= x 2 + 4y 2 + 16z 2 + 4xy + 16yz + 8 zx

(ii) (2x – y + z) 2 = (2x) 2 + (- y) 2 + z 2 + 2 (2x) (- y)+ 2 (- y) (z) + 2 (z) (2x)
= 4x 2 + y 2 + z 2 – 4xy – 2yz + 4zx

(iii) (- 2x + 3y + 2z) 2 = (- 2x) 2 + (3y) 2 + (2z) 2 + 2 (- 2x) (3y)+ 2 (3y) (2z) + 2 (2z) (- 2x)
= 4x 2 + 9y 2 + 4z 2 – 12xy + 12yz – 8zx

(iv) (3a -7b- c) 2 = (3a) 2 + (- 7b) 2 + (- c) 2 + 2 (3a) (- 7b) + 2 (- 7b) (- c) + 2 (- c) (3a)
= 9a 2 + 49b 2 + c 2 - 42ab + 14bc - 6ac

(v)(- 2x + 5y- 3z) 2 = (- 2x) 2 + (5y) 2 + (- 3z) 2 + 2 (- 2x) (5y) + 2 (5y) (- 3z) + 2 (- 3z) (- 2x)
= 4x 2 + 25y 2 + 9z 2 – 20xy – 30yz + 12zx

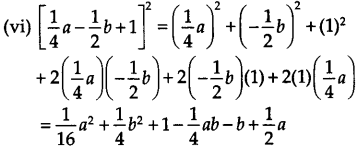
प्रश्न 5.
गुणनखंड कीजिए
(i) 4 x 2 + 9y 2 + 16z 2 + 12xy – 24yz – 16xz
(ii) 2x 2 + y 2 + 8z 2 – 2√2xy + 4√2yz – 8xz
हल:
(i) 4x 2 + 9y 2 + 16z 2 + 12xy – 24yz – 16xz
= (2x) 2 + (3y) 2 + (- 4z) 2 + 2 (2x) (3y) + 2 (3y) (- 4z) + 2 (- 4z) (2x)
= (2x + 3y – 4z) 2 = (2x + 3y + 4z) (2x + 3y – 4z)

(ii) 2x 2 + y 2 + 8z 2 – 2√2xy + 4√2yz – 8xz
= (- √2x) 2 + (y) 2 + (2 √2z) 2 y + 2(- √2x) (y)+ 2 (y) (2√2z) + 2 (2√2z) (- √2x)
= (- √2x + y + 2 √2z) 2
= (- √2x + y + 2 √2z) (- √2x + y + 2 √2z)

प्रश्न 6.
निम्नलिखित घनों को विस्तारित रूप में लिखिए।

हल:
हमारे पास है, (x + y) 3 = x 3 + y 3 + 3xy(x + y) …(1)
और (x – y) 3 = x 3 – y 3 – 3xy(x – y) …(2)

(i) (2x + 1) 3 = (2x) 3 + (1) 3 + 3(2x)(1)(2x + 1) [(1) से]
= 8x 3 + 1 + 6x(2x + 1)
= 8x 3 + 12x 2 + 6x + 1

(ii) (2ए - 3बी) 3 = (2ए) 3 - (3बी) 3 - 3(2ए)(3बी)(2ए - 3बी) [बाय (2)]
= 8ए 3 - 27बी 3 - 18एबी(2ए - 3बी)
= 8 ए 3 - 27बी 3 - 36ए 2 बी + 54एबी 2

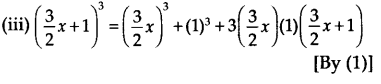
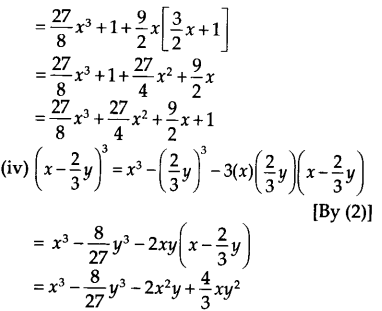
प्रश्न 7.
उपयुक्त सर्वसमिकाओं का प्रयोग करके निम्नलिखित का मूल्यांकन करें
(i) (99) 3
(ii) (102) 3
(iii) (998) 3
हल:
(i) हमारे पास है, 99 = (100 -1)
∴ 99 3 = (100 – 1) 3
= (100) 3 – 1 3 – 3(100)(1)(100 -1)
[(a – b) 3 = a 3 – b 3 – 3ab (a – b) का प्रयोग करते हुए]
= 1000000 – 1 – 300(100 – 1)
= 1000000 -1 – 30000 + 300
= 1000300 – 30001 = 970299

(ii) हमारे पास है, 102 =100 + 2
∴ 102 3 = (100 + 2) 3
= (100) 3 + (2) 3 + 3(100)(2)(100 + 2)
[(a + b) 3 = a 3 + b 3 + 3ab (a + b) का उपयोग करते हुए]
= 1000000 + 8 + 600(100 + 2)
= 1000000 + 8 + 60000 + 1200 = 1061208

(iii) हमारे पास है, 998 = 1000 – 2
∴ (998) 3 = (1000-2) 3
= (1000) 3 – (2) 3 – 3(1000)(2)(1000 – 2)
[(a – b) का उपयोग करते हुए 3 = a 3 – b 3 – 3ab (a – b)]
= 1000000000 – 8 – 6000(1000 – 2)
= 1000000000 – 8 – 6000000 +12000
= 994011992

प्रश्न 8.
निम्नलिखित में से प्रत्येक का गुणनखंड कीजिए
(i) 8a 3 +b 3 + 12a 2 b+6ab 2
(ii) 8a 3 -b 3 -12a 2 b+6ab 2
(iii) 27-125a 3 -135a+225a 2
(iv) 64a 3 -27b 3 -144a 2 b + 108ab 2

हल:
(i) 8a 3 +b 3 +12a 2 b+6ab 2
= (2a) 3 + (b) 3 + 6ab(2a + b)
= (2a) 3 + (b) 3 + 3(2a)(b)(2a + b)
= (2 a + b) 3 [a 3 + b 3 + 3 ab(a + b) = (a + b) 3
का उपयोग करके ] = (2a + b)(2a + बी)(2ए + बी)

(ii) 8a 3 – b 3 – 12o 2 b + 6ab 2
= (2a) 3 – (b) 3 – 3(2a)(b)(2a – b)
= (2a – b) 3 [a 3 + b 3 + 3 ab(a + b) = (a + b) 3
का उपयोग करके ] = (2a – b) (2a – b) (2a – b)

(iii) 27 – 125a 3 – 135a + 225a 2
= (3) 3 – (5a) 3 – 3(3)(5a)(3 – 5a)
= (3 – 5a) 3
[a 3 + b 3 + 3 ab(a + b) = (a + b) 3 ]
= (3 – 5a) (3 – 5a) (3 – का प्रयोग करके) 5ए)

(iv) 64a 3 -27b 3 -144a 2 b + 108ab 2
= (4a) 3 - (3b) 3 - 3(4a)(3b)(4a - 3b)
= (4a - 3b) 3 [a 3 - b 3 - 3 ab(a - b) = (a - b) 3 ] = (4a -
का प्रयोग करते हुए ) 3बी)(4ए - 3बी)(4ए - 3बी)

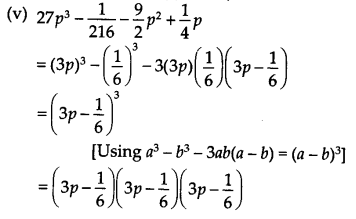
प्रश्न 9.
सत्यापित करें
(i) x 3 + y 3 = (x + y)-(x 2 – xy + y 2 )
(ii) x 3 – y 3 = (x – y) (x 2 + xy + y 2 )
हल:
(i) ∵ (x + y) 3 = x 3 + y 3 + 3xy(x + y)
⇒ (x + y) 3 – 3(x + y)(xy) = x 3 + y 3
⇒ (x + y)[(x + y)2-3xy] = x 3 + y 3
⇒ (x + y)(x 2 + y 2 – xy) = x 3 + y 3
अतः, सत्यापित।

(ii) ∵ (x – y) 3 = x 3 – y 3 – 3xy(x – y)
⇒ (x – y) 3 + 3xy(x – y) = x 3 – y 3
⇒ (x – y)[(x – y) 2 + 3xy)] = x 3 – y 3
⇒ (x – y)(x 2 + y 2 + xy) = x 3 – y 3
अतः, सत्यापित।

प्रश्न 10.
निम्नलिखित में से प्रत्येक का गुणनखंड कीजिए
(i) 27y 3 + 125z 3
(ii) 64m 3 – 343n 3
[संकेत प्रश्न 9 देखें]
हल:
(i) हम जानते हैं कि
x 3 + y 3 = (x + y)(x 2 – xy + y 2 )
हमारे पास है, 27y 3 + 125z 3 = (3y) 3 + (5z) 3
= (3y + 5z)[(3y) 2 – (3y)(5z) + (5z) 2 ]
= (3y + 5z)(9y 2 – 15yz + 25z 2 )

(ii) हम जानते हैं कि
x 3 – y 3 = (x – y)(x 2 + xy + y 2 )
हमारे पास है, 64m 3 – 343n 3 = (4m) 3 – (7n) 3
= (4m – 7n)[(4m) 2 + (4m)(7n) + (7n) 2 ]
= (4m – 7n)(16m 2 + 28एमएन + 49एन 2 )

प्रश्न 11.
27x 3 +y 3 +z 3 -9xyz का गुणनखंड कीजिए।
समाधान:
हमारे पास है,
27x 3 + y 3 + z 3 – 9xyz = (3x) 3 + (y) 3 + (z) 3 – 3(3x)(y)(z)
पहचान का उपयोग करते हुए,
x 3 + y 3 + z 3 – 3xyz = (x + y + z)(x 2 + y 2 + z 2 – xy – yz – zx)
हमारे पास है, (3x) 3 + (y) 3 + (z) 3 – 3(3x)(y)(z)
= (3x + y + z)[(3x) 3 + y 3 + z 3 – (3x × y) – (y × 2) – (z × 3x)]
= (3x + y + z)(9x 2 + y 2 + z 2 – 3xy – yz – 3zx)

प्रश्न 12.
सत्यापित करें कि
x 3 +y 3 +z 3 – 3xyz =12(x + y+z)[(xy) 2 + (y – z) 2 +(z – x) 2 ]
हल:
दायाँ पक्ष
=12(x + y + z)[(x – y) 2 +(y – z) 2 +(z – x) 2 ]
=12(x + y + 2)[(x 2 + y 2 – 2xy) + (y 2 + z 2 – 2yz) + (z 2 + x 2 – 2zx)]
=12(x + y + 2)(x 2 + y 2 + y 2 + z 2 + z 2 + x 2 – 2xy – 2yz – 2zx)
=12(x + y + z)[2(x 2 + y 2 + z 2 – xy – yz – zx)]
= 2 x12x (x + y + z)(x 2 + y 2 + z 2 – xy – yz – zx)
= (x + y + z)(x 2 + y 2 + z 2 – xy – yz – zx)
= x 3 + y 3 + z 3 – 3xyz = बायाँ पक्ष
अतः, सत्यापित।

प्रश्न 13.
यदि x + y + z = 0, तो दर्शाइए कि x 3 + y 3 + z 3 = 3 xyz है।
हल:
चूँकि, x + y + z = 0
⇒ x + y = -z (x + y) 3 = (-z) 3
⇒ x 3 + y 3 + 3xy(x + y) = -z 3
⇒ x 3 + y 3 + 3xy(-z) = -z 3 [∵ x + y = -z]
⇒ x 3 + y 3 – 3xyz = -z 3
⇒ x 3 + y 3 + z 3 = 3xyz
अतः, यदि x + y + z = 0, तो
x 3 + y 3 + z 3 = 3xyz

प्रश्न 14.
घनों की वास्तविक गणना किए बिना, निम्नलिखित में से प्रत्येक का मान ज्ञात कीजिए
(i) (- 12) 3 + (7) 3 + (5) 3
(ii) (28) 3 + (- 15) 3 + (- 13) 3
हल:
(i) हमें मिलता है, (-12) 3 + (7) 3 + (5) 3
मान लीजिए x = -12, y = 7 और z = 5.
तो, x + y + z = -12 + 7 + 5 = 0
हम जानते हैं कि यदि x + y + z = 0, तो, x 3 + y 3 + z 3 = 3xyz
∴ (-12) 3 + (7) 3 + (5) 3 = 3[(-12)(7)(5)]
= 3[-420] = -1260

(ii) हमें प्राप्त है, (28) 3 + (-15) 3 + (-13) 3
मान लीजिए x = 28, y = -15 और z = -13 है।
तो, x + y + z = 28 – 15 – 13 = 0
हम जानते हैं कि यदि x + y + z = 0 है, तो x 3 + y 3 + z 3 = 3xyz
∴ (28) 3 + (-15) 3 + (-13) 3 = 3(28)(-15)(-13)
= 3(5460) = 16380

प्रश्न 15.
निम्नलिखित प्रत्येक आयत की लंबाई और चौड़ाई के लिए संभावित व्यंजक दीजिए, जिसमें उनके क्षेत्रफल दिए गए हैं
(i) क्षेत्रफल 25a 2 – 35a + 12
(ii) क्षेत्रफल 35y 2 + 13y – 12
हल:
आयत का क्षेत्रफल = (लंबाई) x (चौड़ाई)
(i) 25a 2 – 35a + 12 = 25a 2 – 20a – 15a + 12 = 5a(5a – 4) – 3(5a – 4) = (5a – 4)(5a – 3)
इस प्रकार, संभावित लंबाई और चौड़ाई (5a – 3) और (5a – 4) हैं।

(ii) 35y 2 + 13y -12 = 35y 2 + 28y – 15y -12
= 7y(5y + 4) – 3(5y + 4) = (5 y + 4)(7y – 3)
इस प्रकार, संभावित लंबाई और चौड़ाई (7y – 3) और (5y + 4) हैं।

प्रश्न 16.
नीचे दिए गए आयतनों वाले घनाभों के आयामों के लिए संभावित व्यंजक क्या हैं?
(i) आयतन 3x 2 – 12x
(ii) आयतन 12ky 2 + 8ky – 20k
हल:
घनाभ का आयतन = (लंबाई) x (चौड़ाई) x (ऊँचाई)
(i) हमारे पास है, 3x 2 – 12x = 3(x 2 – 4x)
= 3 xxx (x – 4)
∴ घनाभ के संभावित आयाम 3, x और (x – 4) हैं।

(ii) हमारे पास है, 12ky 2 + 8ky – 20k
= 4[3ky 2 + 2ky – 5k] = 4[k(3y 2 + 2y – 5)]
= 4 xkx (3y 2 + 2y – 5)
= 4k[3y 2 – 3y + 5y – 5]
= 4k[3y(y – 1) + 5(y – 1)]
= 4k[(3y + 5) x (y – 1)]
= 4k x (3y + 5) x (y – 1)
इस प्रकार, घनाभ के संभावित आयाम 4k, (3y + 5) और (y -1) हैं।