NCERT Class 9 Maths Chapter 3 निर्देशांक ज्यामिति
NCERT Solutions for Class 9 Maths Chapter 3 निर्देशांक ज्यामिति
Ex 3.1
प्रश्न 1.
आप अपनी अध्ययन मेज पर रखे टेबल लैंप की स्थिति किसी अन्य व्यक्ति को कैसे बताएँगे?
हल:
मेज पर रखे टेबल लैंप की स्थिति बताने के लिए, आइए टेबल लैंप को P और मेज को एक समतल मानें।
अब मेज के दो लंबवत किनारों को अक्ष OX और OY के रूप में चुनें।
OY से P (लैंप) की लंबवत दूरी 'a' सेमी मापें। OX से P (लैंप) की लंबवत दूरी 'b' सेमी मापें।
इस प्रकार, टेबल लैंप P की स्थिति क्रमित युग्म (a, b) द्वारा वर्णित है।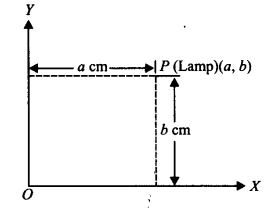
प्रश्न 2.
(सड़क योजना): एक शहर में दो मुख्य सड़कें हैं जो शहर के केंद्र में एक दूसरे को काटती हैं। ये दोनों सड़कें उत्तर-दक्षिण दिशा और पूर्व-पश्चिम दिशा में हैं। शहर की अन्य सभी सड़कें इन सड़कों के समानांतर चलती हैं और 200 मीटर की दूरी पर हैं। प्रत्येक दिशा में 5 सड़कें हैं। 1 सेमी = 200 मीटर का उपयोग करके, अपनी नोटबुक पर शहर का एक मॉडल बनाएं। सड़कों/गलियों को एकल रेखाओं द्वारा दर्शाएं।
आपके मॉडल में कई क्रॉस-स्ट्रीट हैं। एक विशेष क्रॉस-स्ट्रीट दो सड़कों से बनी है, एक उत्तर-दक्षिण दिशा में और दूसरी पूर्व-पश्चिम दिशा में चलती है। प्रत्येक क्रॉस स्ट्रीट को निम्नलिखित तरीके से संदर्भित किया जाता है: यदि उत्तर-दक्षिण दिशा में चलने वाली दूसरी सड़क और पूर्व-पश्चिम दिशा में चलने वाली 5 वीं सड़क किसी चौराहे पर मिलती है, तो हम इस क्रॉस-स्ट्रीट को (2,5) कहेंगे। इस सम्मेलन का उपयोग करके, खोजें:
(i) कितनी क्रॉस-स्ट्रीट को (4,3) के रूप में संदर्भित किया जा सकता है।
(ii) कितनी क्रॉस-स्ट्रीटों को (3,4) कहा जा सकता है।
हल:
(i) बिंदु A(4, 3) द्वारा दर्शाई गई एक अद्वितीय क्रॉस स्ट्रीट।
(ii) बिंदु B(3,4) द्वारा दर्शाई गई एक अद्वितीय क्रॉस स्ट्रीट।
ये दो क्रॉस स्ट्रीट विशिष्ट रूप से पाई जाती हैं क्योंकि हमने उन्हें खोजने के लिए दो संदर्भ रेखाओं का उपयोग किया है।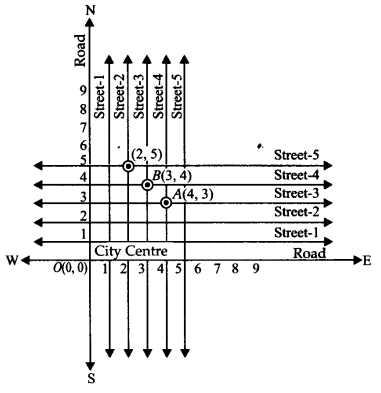
Ex 3.2
प्रश्न 1
निम्नलिखित प्रत्येक प्रश्न का उत्तर लिखिए:
(i) कार्तीय तल में किसी बिंदु की स्थिति निर्धारित करने के लिए खींची गई क्षैतिज और ऊर्ध्वाधर रेखाओं का नाम क्या है?
(ii) इन दो रेखाओं द्वारा बने तल के प्रत्येक भाग का नाम क्या है?
(iii) उस बिंदु का नाम लिखिए जहाँ ये दोनों रेखाएँ प्रतिच्छेद करती हैं।
हल:
(i) क्षैतिज रेखा: x-अक्ष और ऊर्ध्वाधर रेखा: y-अक्ष।
(ii) प्रत्येक भाग को "चतुर्थांश" कहा जाता है।
(iii) मूल बिंदु
प्रश्न 2
दी गई आकृति को देखिए और निम्नलिखित लिखिए:
(i) B के निर्देशांक।
(ii) C के निर्देशांक।
(iii) निर्देशांकों (-3,-5) द्वारा पहचाना गया बिंदु।
(iv) निर्देशांकों (2,-4) द्वारा पहचाना गया बिंदु।
(v) बिंदु D का भुज।
(vi) बिंदु H की कोटि।
(vii) बिंदु L के निर्देशांक।
(viii) बिंदु M के निर्देशांक।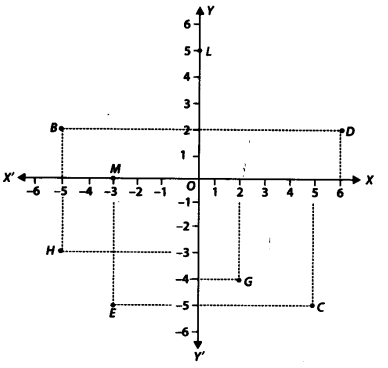
हल:
आकृति से, हमें प्राप्त है:
(i) B के निर्देशांक (-5,2) हैं।
(ii) C के निर्देशांक (5,-5) हैं।
(iii) बिंदु E निर्देशांकों (-3,-5) द्वारा पहचाना गया है।
(iv) बिंदु G निर्देशांकों (2,-4) द्वारा पहचाना गया है। (v)
बिंदु D का भुज 6 है।
(vi) बिंदु H की कोटि -3 है।
(vii) बिंदु L के निर्देशांक (0,5) हैं। (viii) बिंदु M के निर्देशांक (-3,0) हैं।
Ex 3.3
प्रश्न 1
बिंदु (-2, 4), (3, -1), (-1, 0), (1, 2) और (-3, -5) में से प्रत्येक किस चतुर्थांश या किस अक्ष पर स्थित हैं? कार्तीय तल पर उन्हें स्थित करके अपने उत्तर की पुष्टि करें।
हल:
बिंदु (-2, 4) में ऋणात्मक भुज और धनात्मक कोटि है।
∴ (-2,4) दूसरे चतुर्थांश में स्थित है । बिंदु
(3, -1) में धनात्मक भुज और ऋणात्मक कोटि है।
∴ (3, -1) चौथे चतुर्थांश में स्थित है।
बिंदु (-1, 0) में ऋणात्मक भुज और शून्य कोटि है।
∴ बिंदु (-1, 0) ऋणात्मक x-अक्ष पर स्थित है।
बिंदु (1, 2) में भुज के साथ-साथ कोटि भी धनात्मक है।
∴ बिंदु (1,2) प्रथम चतुर्थांश में स्थित है । बिंदु
(-3, -5) का भुज और कोटि दोनों ऋणात्मक हैं।
∴ बिंदु (-3, -5) तृतीय चतुर्थांश में स्थित है।
इन बिंदुओं को कार्तीय तल में निम्न आकृति में दर्शाए अनुसार अंकित किया गया है: A(-2, 4); B(3, -1); C(-1, 0); D(1, 2) और E (-3, -5)।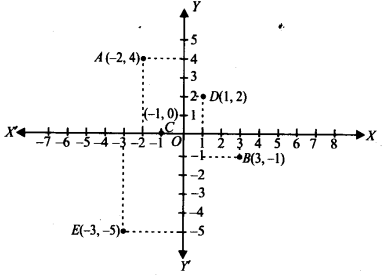
प्रश्न 2
निम्न सारणी में दिए गए बिंदुओं (x, y) को समतल पर आलेखित कीजिए, अक्षों पर दूरी की उपयुक्त इकाइयाँ चुनिए।
हल:
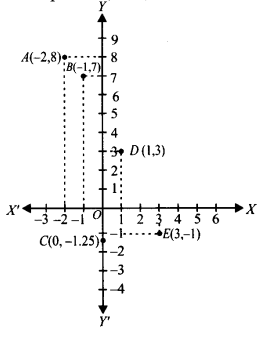
दिए गए बिंदु (-2, 8), (-1, 7), (0, -1.25), (1,3) और (3, -1) हैं।
इन बिंदुओं को आलेखित करने के लिए:
(i) हम X'OX और YOY' को अक्षों के रूप में खींचते हैं।
(ii) हम अक्षों पर दूरी की उपयुक्त इकाइयाँ चुनते हैं।
(iii) (-2,8) को आलेखित करने के लिए, हम O से शुरू करते हैं, x-अक्ष पर (-2) इकाइयाँ लेते हैं और फिर y-अक्ष पर (+8) इकाइयाँ लेते हैं। हम बिंदु को A (-2, 8) से चिह्नित करते हैं।
(iv) (-1,7) को आलेखित करने के लिए, हम O से शुरू करते हैं, x-अक्ष पर (-1) इकाई लेते हैं और फिर y-अक्ष पर (+7) इकाई लेते हैं। हम बिंदु को B(-1, 7) से चिह्नित करते हैं।
(v) (0, -1.25) को आलेखित करने के लिए, हम y-अक्ष पर x-अक्ष से 1.25 इकाई नीचे चलते हैं और बिंदु को C(0, -1.25) से चिह्नित करते हैं।
(vi) (1, 3) को आलेखित करने के लिए, हम x-अक्ष पर (+1) इकाई लेते हैं और फिर y-अक्ष पर (+3) इकाई लेते हैं। हम बिंदु को D(1, 3) से चिह्नित करते हैं।
(vii) (3, -1) को आलेखित करने के लिए, हम x-अक्ष पर (+3) इकाई लेते हैं और फिर y-अक्ष पर (-1) इकाई लेते हैं। हम बिंदु E(3, -1) से चिह्नित करते हैं।