NCERT Class 9 Maths Chapter 4 दो चरों में रैखिक समीकरण
NCERT Solutions for Class 9 Maths Chapter 4 दो चरों में रैखिक समीकरण
Ex 4.1
प्रश्न 1.
एक नोटबुक का मूल्य एक पेन के मूल्य का दोगुना है। इस कथन को निरूपित करने के लिए दो चरों में एक रैखिक समीकरण लिखिए।
(एक नोटबुक का मूल्य x रुपये और एक पेन का मूल्य y रुपये लीजिए)।
हल:
माना नोटबुक का मूल्य = x रुपये
और एक पेन का मूल्य = y रुपये है।
शर्त के अनुसार, हमारे पास है
[एक नोटबुक का मूल्य] = 2 x [एक पेन का मूल्य]
i. e„ (x) = 2 x (y) या, x = 2y
या, x – 2y = 0
इस प्रकार, अभीष्ट रैखिक समीकरण x – 2y = 0 है।
Ex 4.1 कक्षा 9 गणित प्रश्न 2
निम्नलिखित रैखिक समीकरणों को ax + by + c = 0 के रूप में व्यक्त करें और प्रत्येक स्थिति में a, b और c के मान इंगित करें:
(i) 2x + 3y =
(ii)
(iii) – 2x + 3y = 6
(iv) x = 3y
(v) 2x = -5y
(vi) 3x + 2 = 0
(vii) y – 2 = 0
(viii) 5 = 2x
हल:
(i) हमारे पास है 2x + 3y =
या (2)x + (3)y + (
इसकी तुलना ax + by से करने पर +c= 0, हमें a = 2,
b = 3 और c= –
(ii) हमारे पास है
या x + (-
इसकी तुलना ax + by + c = 0 से करने पर, हमें
a =1, b =-
(iii) हमारे पास -2x + 3y = 6 या (-2)x + (3)y + (-6) = 0 है।
इसकी तुलना ax – 4 – by + c = 0 से करने पर, हमें a = -2, b = 3 और c = -6 प्राप्त होता है।
(iv) हमारे पास x = 3y या (1)x + (-3)y + (0) = 0 है। इसकी तुलना ax + by + c = 0 से करने पर, हमें a = 1, b = -3 और c = 0 मिलता है।
(v) हमारे पास 2x = -5y या (2)x + (5)y + (0) = 0 है। इसकी तुलना ax + by + c = 0 से करने पर, हमें a = 2, b = 5 और c = 0 मिलता है। (vi) हमारे पास 3x + 2 = 0 या (3)x + (0)y + (2) = 0 है। इसकी तुलना ax + by + c = 0 से करने पर, हमें a = 3, b = 0 और c = 2 मिलता है। (vii) हमारे पास y – 2 = 0 या (0)x + (1)y + (-2) = 0 है। इसकी तुलना ax + by + c = 0 से करने पर, हमें a = 0, b = 1 और मिलता है। c = -2. (viii) हमारे पास है 5 = 2x ⇒ 5 – 2x = 0 या -2x + 0y + 5 = 0 या (-2)x + (0)y + (5) = 0 इसकी तुलना ax + by + c = 0 से करने पर, हमें a = -2, b = 0 और c = 5 मिलता है।
Ex 4.2
प्रश्न 1
निम्नलिखित में से कौन सा विकल्प सत्य है और क्यों?
y = 3x + 5 के
(i) एक अद्वितीय हल है,
(ii) केवल दो हल हैं,
(iii) अपरिमित रूप से अनेक हल हैं।
हल:
विकल्प (iii) सत्य है क्योंकि दिए गए समीकरण में x के प्रत्येक मान के लिए, हमें y का एक संगत मान प्राप्त होता है और इसके विपरीत भी।
अतः दिए गए रैखिक समीकरण के अपरिमित रूप से अनेक हल हैं।
प्रश्न 2
निम्नलिखित समीकरणों में से प्रत्येक के लिए चार हल लिखें:
(i) 2x + y = 7
(ii) πx + y = 9
हल:
(i) 2x + y = 7
जब x = 0, 2(0) + y = 7 ⇒ y = 7
∴ हल (0, 7) है
जब x =1, 2(1) + y = 7 ⇒ y = 7 – 2 ⇒ y = 5
∴ हल (1, 5) है
जब x = 2, 2(2) + y =7y = 7 – 4 ⇒ y = 3
∴ हल (2, 3) है
जब x = 3, 2(3) + y = 7y = 7 – 6 ⇒ y = 1
∴ हल (3, 1) है।
(ii) πx + y = 9
जब x = 0, π(0) + y = 9 ⇒ y = 9 – 0 ⇒ y = 9
∴ हल (0, 9) है
जब x = 1, π(1) + y = 9 ⇒ y = 9 – π
∴ हल (1, (9 – π)) है
जब x = 2, π(2) + y = 9 ⇒ y = 9 – 2π
∴ हल (2, (9 – 2π)) है
जब x = -1, π(-1) + y = 9 ⇒ y = 9 + π
∴ हल (-1, (9 + π)) है
प्रश्न 3
जाँच कीजिए कि निम्नलिखित में से कौन-से समीकरण x – 2y = 4 के हल हैं और कौन-से नहीं हैं:
(i) (0,2)
(ii) (2,0)
(iii) (4, 0)
(iv) (√2, 4√2)
(v) (1, 1)
हल:
(i) (0,2) का अर्थ है x = 0 और y = 2
x – 2y = 4 में x = 0 और y = 2 रखने पर, हमें
LHS = 0 – 2(2) = -4 प्राप्त होता है।
लेकिन RHS = 4
∴ LHS ≠ RHS
∴ x = 0, y = 2 कोई हल नहीं है।
(ii) (2, 0) का अर्थ है x = 2 और y = 0
x – 2y = 4 में x = 2 और y = 0 रखने पर, हमें
LH:S प्राप्त होता है। 2 – 2(0) = 2 – 0 = 2.
लेकिन RHS = 4
∴ LHS ≠ RHS
∴ (2,0) एक हल नहीं है।
(iii) (4, 0) का अर्थ है x = 4 और y = 0
x – 2y = 4 में x = 4 और y = o रखने पर, हमें प्राप्त होता है
LHS = 4 – 2(0) = 4 – 0 = 4 =RHS
∴ LHS = RHS
∴ (4, 0) एक हल है।
(iv) (√2, 4√2) का अर्थ है x = √2 और y = 4√2
x – 2y = 4 में x = √2 और y = 4√2 रखने पर, हमें प्राप्त होता है
बायाँ पक्ष = √2 – 2(4√2) = √2 – 8√2 = -7√2
लेकिन दायाँ पक्ष = 4
∴ बायाँ पक्ष ≠ दायाँ पक्ष
∴ (√2, 4√2) एक हल नहीं है।
(v) (1, 1) का अर्थ है x = 1 और y = 1
x – 2y = 4 में x = 1 और y = 1 रखने पर, हमें प्राप्त होता है
: बायाँ पक्ष = 1 – 2(1) = 1 – 2 = -1. लेकिन दायाँ पक्ष = 4
∴ बायाँ पक्ष ≠ दायाँ पक्ष
∴ (1, 1) एक हल नहीं है।
प्रश्न 4
k का मान ज्ञात कीजिए, यदि x = 2, y = 1 समीकरण 2x + 3y = k का एक हल है।
हल:
हमारे पास 2x + 3y = k है,
2x + 3y = k में x = 2 और y = 1 रखने पर, हमें प्राप्त होता है
2(2) + 3(1) ⇒ k = 4 + 3 – k ⇒ 7 = k
इस प्रकार, k का अभीष्ट मान 7 है।
Ex 4.3
प्रश्न 1
दो चरों वाले निम्नलिखित रैखिक समीकरणों में से प्रत्येक का आलेख खींचिए:
(i) x + y = 4
(ii) x – y = 2
(iii) y = 3x
(iv) 3 = 2x + y
हल:
(i) x + y = 4 ⇒ y = 4 – x
यदि x = 0 है, तो y = 4 – 0 = 4
x = 1, तो y = 4 – 1 = 3
x = 2, तो y = 4 – 2 = 2
∴ हमें निम्नलिखित तालिका प्राप्त होती है: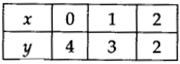
क्रमित युग्मों (0, 4), (1,3) और (2,2) को आलेखित कीजिए। इन बिंदुओं को मिलाने पर, हमें एक सीधी रेखा AB प्राप्त होती है जैसा कि दिखाया गया है।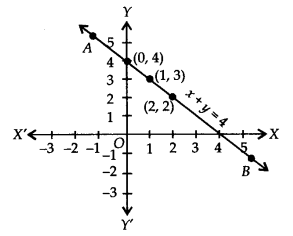
इस प्रकार, रेखा AB, x + y = 4 का अभीष्ट आलेख है।
(ii) x – y = 2 ⇒ y = x – 2
यदि x = 0 है, तो y = 0 – 2 = -2
x = 1 है, तो y = 1 – 2 = -1
x = 2 है, तो y = 2 – 2 = 0
∴ हमें निम्नलिखित तालिका प्राप्त होती है: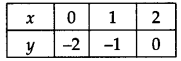
क्रमित युग्मों (0, -2), (1, -1) और (2, 0) को ग्राफ पेपर पर अंकित कीजिए। इन बिंदुओं को मिलाने पर, हमें चित्र में दिखाए अनुसार एक सीधी रेखा PQ प्राप्त होती है।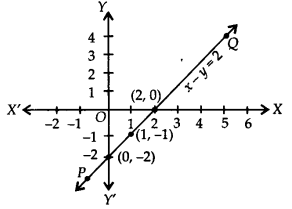
इस प्रकार, दिया गया समय x – y = 2 का अभीष्ट ग्राफ है।
(iii) y = 3x
यदि x = 0 है,
तो y = 3(0) ⇒ y = 0
x = 1, तो y = 3(1) = 3
x = -1, तो y = 3(-1) = -3
∴ हमें निम्नलिखित तालिका प्राप्त होती है: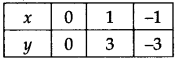
क्रमित युग्मों (0, 0), (1, 3) और (-1, -3) को ग्राफ पेपर पर आलेखित कीजिए। इन बिंदुओं को मिलाने पर, हमें चित्र में दर्शाई गई एक सीधी रेखा LM प्राप्त होती है।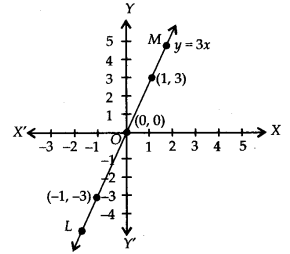
इस प्रकार, रेखा LM, y = 3x का अभीष्ट ग्राफ है।
(iv) 3 = 2x + y ⇒ y = 3 – 2x
यदि x = 0 है, तो y = 3 – 2(0) = 3
x = 1, तो y = 3 – 2(1) = 3 – 2 = 1
x = 2, तो y = 3 – 2(2) = 3 – 4 = -1
∴ हमें निम्नलिखित तालिका प्राप्त होती है:
क्रमित युग्मों (0, 3), (1, 1) और (2, - 1) को ग्राफ पेपर पर आलेखित कीजिए। इन बिंदुओं को मिलाने पर, हमें एक सीधी रेखा CD प्राप्त होती है, जैसा कि चित्र में दिखाया गया है।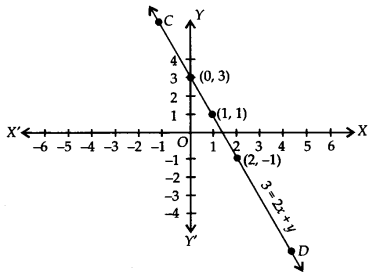
इस प्रकार, रेखा CD, 3 = 2x + y का अभीष्ट ग्राफ है।
प्रश्न 2 बिंदु (2, 14) से होकर जाने वाली दो रेखाओं के समीकरण दीजिए। ऐसी और कितनी रेखाएँ हैं और क्यों?
हल:
(2, 14) का अर्थ है x = 2 और y = 14।
(2, 14) के हल वाले समीकरण हैं: (i) x + y = 16, (ii) 7x – y = 0
बिंदु (2, 14) से होकर जाने वाली रेखाओं की संख्या अनंत है, क्योंकि एक बिंदु से होकर अनंत रेखाएँ खींची जा सकती हैं।
प्रश्न 3
यदि बिंदु (3, 4) समीकरण 3y = ax + 7 के ग्राफ पर स्थित है, तो a का मान ज्ञात कीजिए।
हल:
दी गई रेखा का समीकरण 3y = ax + 7 है
∵ (3, 4) दी गई रेखा पर स्थित है।
∴ इसे समीकरण 3y = ax + 7 को संतुष्ट करना होगा।
हमारे पास है, (3, 4) ⇒ x = 3 और y = 4।
इन मानों को दिए गए समीकरण में रखने पर, हम प्राप्त करते हैं
3 x 4 = ax 3 + 7
⇒ 12 = 3a + 7
⇒ 3a = 12 – 7 = 5 ⇒ a = \(\frac { 5 }{ 3 }\)
इस प्रकार, a का अभीष्ट मान \(\frac { 5 }{ 3 }\) है
प्रश्न 4
एक शहर में टैक्सी का किराया इस प्रकार है: पहले किलोमीटर के लिए किराया 8 रुपये है और उसके बाद की दूरी के लिए यह 5 रुपये प्रति किमी है। तय की गई दूरी को x किमी और कुल किराया y रुपये मानकर, इस जानकारी के लिए एक रैखिक समीकरण लिखिए और इसका ग्राफ खींचिए।
हल:
यहाँ, तय की गई कुल दूरी = x किमी और कुल टैक्सी किराया = y रुपये
1 किमी का किराया = 8 रुपये
शेष दूरी = (x – 1) किमी
∴ (x – 1) किमी का किराया = 5 रुपये x(x – 1)
कुल टैक्सी किराया = 8 रुपये + 5 रुपये (x – 1)
प्रश्न के अनुसार,
y = 8 + 5(x – 1) = y = 8 + 5x – 5
⇒ y = 5x + 3,
जो दी गई जानकारी को दर्शाने वाला अभीष्ट रैखिक समीकरण है।
ग्राफ़: हमारे पास है y = 5x + 3
जब x = 0, तो y = 5(0) + 3 ⇒ y = 3
x = -1, तो y = 5(-1) + 3 ⇒ y = -2
x = -2, तो y = 5(-2) + 3 ⇒ y = -7
∴ हमें निम्नलिखित तालिका प्राप्त होती है:
अब, क्रमित युग्मों (0, 3), (-1, -2) और (-2, -7) को एक ग्राफ़ पेपर पर आलेखित करके और उन्हें जोड़कर, हमें एक सीधी रेखा PQ प्राप्त होती है जैसा कि चित्र में दिखाया गया है।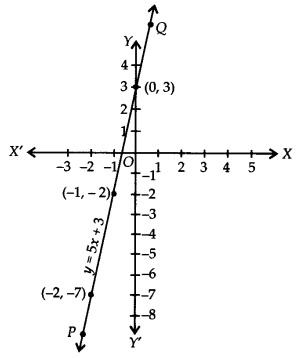
इस प्रकार, रेखा PQ रैखिक समीकरण y = 5x + 3 का अभीष्ट ग्राफ़ है।
प्रश्न 5
नीचे दिए गए विकल्पों में से वह समीकरण चुनिए जिसके ग्राफ चित्र (1) और चित्र (2) में दिए गए हैं।
चित्र (1) के लिए
(i) y = x
(ii) x + y = 0
(iii) y = 2x
(iv) 2 + 3y = 7x
आकृति (2) के लिए
(i) y = x + 2
(ii) y = x – 2
(iii) y = -x + 2
(iv) x + 2y = 6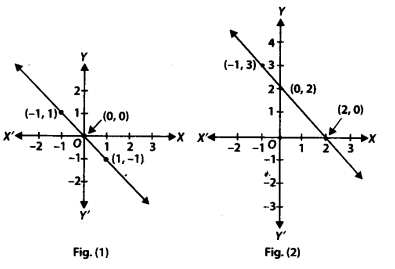
हल:
आकृति (1) के लिए, सही रैखिक समीकरण x + y = 0 है
[क्योंकि (-1, 1) = -1 + 1 = 0 और (1,-1) = 1 + (-1) = 0]
आकृति (2) के लिए, सही रैखिक समीकरण y = -x + 2 है
[क्योंकि (-1,3) 3 = -1(-1) + 2 = 3 = 3 और (0,2)
⇒ 2 = -(0) + 2 ⇒ 2 = 2]
प्रश्न 6
यदि किसी पिंड पर स्थिर बल लगाने पर किया गया कार्य पिंड द्वारा तय की गई दूरी के समानुपाती हो, तो इसे दो चरों वाले समीकरण के रूप में व्यक्त कीजिए और स्थिर बल को 5 इकाई मानकर इसका आलेख खींचिए। आलेख से यह भी पढ़िए कि पिंड द्वारा तय की गई दूरी पर किया गया कार्य
(i) 2 इकाई
(ii) 0 इकाई है
। हल:
स्थिर बल 5 इकाई है।
मान लीजिए कि तय की गई दूरी = x इकाई और किया गया कार्य = y इकाई है।
किया गया कार्य = बल x दूरी
⇒ y = 5 xx ⇒ y = 5x
ग्राफ बनाने के लिए, हमारे पास y = 5x है
जब x = 0, तो y = 5(0) = 0
x = 1, तो y = 5(1) = 5
x = -1, तो y = 5(-1) = -5
∴ हमें निम्नलिखित तालिका मिलती है:
ग्राफ पेपर पर क्रमित युग्मों (0, 0), (1, 5) और (-1, -5) को खींचने और बिंदुओं को जोड़ने पर, हमें एक सीधी रेखा AB प्राप्त होती है जैसा कि दिखाया गया है।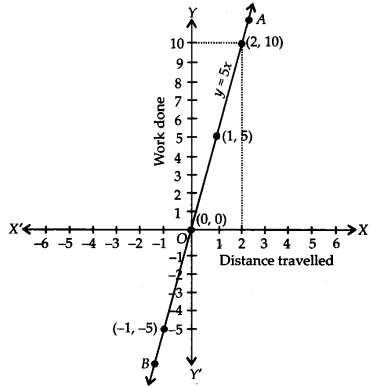
ग्राफ से, हमें मिलता है
(i) तय की गई दूरी = 2 इकाई अर्थात, x = 2
∴ यदि x = 2, तो y = 5(2) = 10
⇒ किया गया कार्य = 10 इकाई।
(ii) तय की गई दूरी = 0 इकाई अर्थात, x = 0
∴ यदि x = 0 ⇒ y = 5(0) – 0
⇒ किया गया कार्य = 0 इकाई।
प्रश्न 7
एक स्कूल की कक्षा 9 की दो छात्राएँ, यामिनी और फ़ातिमा, ने मिलकर भूकंप पीड़ितों की मदद के लिए प्रधानमंत्री राहत कोष में 100 रुपये का योगदान दिया। एक रैखिक समीकरण लिखिए जो इन आँकड़ों को संतुष्ट करता हो। (आप उनके योगदान को x रुपये और y रुपये मान सकते हैं।) इसका ग्राफ़ खींचिए।
हल:
मान लीजिए यामिनी का योगदान = x रुपये
और फ़ातिमा का योगदान = 100 रुपये। y
∴ हमें प्राप्त है x + y = 100 ⇒ y = 100 – x
अब, जब x = 0, y = 100 – 0 = 100
x = 50, y = 100 – 50 = 50
x = 100, y = 100 – 100 = 0
∴ हमें निम्नलिखित तालिका प्राप्त होती है:
क्रमित युग्मों (0,100), (50,50) और (100, 0) को उचित पैमाने का उपयोग करके एक ग्राफ पेपर पर आलेखित करने और इन बिंदुओं को मिलाने पर, हमें एक सीधी रेखा PQ प्राप्त होती है जैसा कि दिखाया गया है।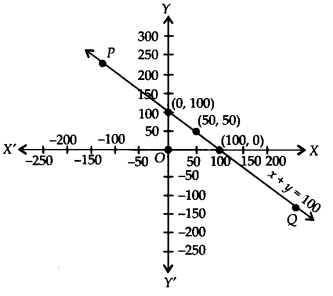
इस प्रकार, रेखा PQ रैखिक समीकरण x + y = 100 का अभीष्ट ग्राफ है।
Ex 4.4
प्रश्न 1
y = 3 के ज्यामितीय निरूपण समीकरण के रूप में दीजिए
(i) एक चर में
(ii) दो चरों में
हल:
(i) y = 3
∵ y = 3 एक चर, अर्थात् केवल y में एक समीकरण है।
∴ y = 3 संख्या रेखा पर एक अद्वितीय हल है जैसा कि नीचे दिखाया गया है: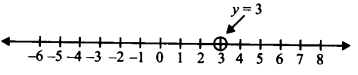
(ii) y = 3
हम y = 3 को दो चरों में इस प्रकार लिख सकते हैं: 0.x + y = 3
अब, जब x = 1, y = 3
x = 2, y = 3
x = -1, y = 3
∴ हमें निम्नलिखित तालिका प्राप्त होती है: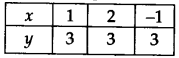
क्रमित युग्मों (1, 3), (2, 3) और (-1, 3) को ग्राफ पेपर पर आलेखित करने और उन्हें जोड़ने पर, हमें 0.x + y = 3,
अर्थात y = 3 के हल के रूप में रेखा AB प्राप्त होती है।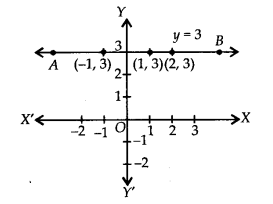
प्रश्न 2
2x + 9 = 0 के ज्यामितीय निरूपण समीकरण के रूप में दीजिए
(i) एक चर में
(ii) दो चरों में
हल:
(i) 2x + 9 = 0
हमें प्राप्त है, 2x + 9 = 0 ⇒ 2x = – 9 ⇒ x = \(\frac { -9 }{ 2 }\)
जो कि एक चर अर्थात् केवल x में एक रैखिक समीकरण है।
इसलिए, x = \(-\frac { 9 }{ 2 }\) संख्या रेखा पर एक अद्वितीय हल है जैसा कि नीचे दिखाया गया है: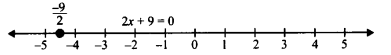
(ii) 2x +9=0
हम 2x + 9 = 0 को दो चरों में 2x + 0, y + 9 = 0
या \(x=\frac { -9-0.y }{ 2 }\) के रूप में लिख सकते हैं
। ∴ जब y = 1, x = \(x=\frac { -9-0(1) }{ 2 }\) = \(-\frac { 9 }{ 2 }\)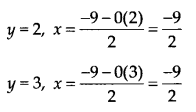
इस प्रकार, हमें निम्नलिखित तालिका मिलती है: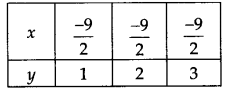
अब, क्रमित युग्मों \((\frac { -9 }{ 2 } ,3)\) ,\((\frac { -9 }{ 2 } ,3)\) और \((\frac { -9 }{ 2 } ,3)\) को ग्राफ पेपर पर आलेखित करने और उन्हें जोड़ने पर, हमें 2x + 9 = 0 के हल के रूप में एक रेखा PQ प्राप्त होती है।