NCERT Class 9 Maths Chapter 5 युक्लिड के ज्यामिति का परिचय
NCERT Solutions for Class 9 Maths Chapter 5 युक्लिड के ज्यामिति का परिचय
Ex 5.1
प्रश्न 1.
निम्नलिखित में से कौन से कथन सत्य हैं और कौन से असत्य हैं? अपने उत्तरों के लिए कारण दीजिए।
(i) केवल एक ही रेखा एकल बिंदु से होकर जा सकती है।
(ii) दो भिन्न बिंदुओं से होकर जाने वाली रेखाओं की अनंत संख्या होती है।
(iii) एक सांत रेखा को दोनों ओर अनिश्चित काल तक बढ़ाया जा सकता है।
(iv) यदि दो वृत्त बराबर हैं, तो उनकी त्रिज्याएँ भी बराबर होती हैं।
(v) आकृति में, यदि AB – PQ और PQ = XY, तो AB = XY।![]()
हल:
(i) असत्य कारण: यदि हम एक कागज़ की सतह पर एक बिंदु 0 अंकित करते हैं। पेंसिल और स्केल का उपयोग करके, हम 0 से
होकर जाने वाली अनंत संख्या में सीधी रेखाएँ खींच सकते हैं।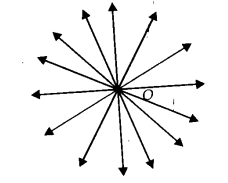
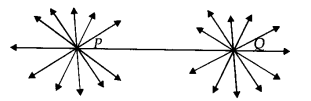
(ii) गलत
कारण: निम्नलिखित आकृति में, P से होकर कई सीधी रेखाएँ गुजर रही हैं। Q से होकर भी कई रेखाएँ गुजर रही हैं। लेकिन केवल एक ही रेखा है जो P के साथ-साथ Q से भी गुजर रही है।
(iii) सही
कारण: अभिधारणा 2 कहती है कि "एक समाप्त रेखा अनिश्चित काल तक उत्पादित की जा सकती है।"
(iv) सही
कारण: एक वृत्त के क्षेत्र को दूसरे वृत्त पर अध्यारोपित करने पर, हम पाते हैं कि वे एक-दूसरे से मिलते हैं। इसलिए, उनके केंद्र और सीमाएँ एक-दूसरे से मिलती हैं।
इस प्रकार, उनकी त्रिज्याएँ एक-दूसरे से मिलती हैं या बराबर होती हैं।
(v) सत्य
कारण: यूक्लिड के अभिगृहीत के अनुसार, जो चीजें एक ही चीज के बराबर हैं वे एक दूसरे के बराबर हैं।
प्रश्न 2.
निम्नलिखित प्रत्येक पद की परिभाषा दीजिए। क्या ऐसे अन्य पद हैं जिन्हें पहले परिभाषित करने की आवश्यकता है? वे क्या हैं और आप उन्हें कैसे परिभाषित कर सकते हैं?
(i) समांतर रेखाएँ
(ii) लंबवत रेखाएँ
(iii) वृत्त की त्रिज्या
(iv) वर्ग
हल:
हाँ, आवश्यक पदों को परिभाषित करने से पहले हमें बिंदु, रेखा, किरण, कोण, तल, वृत्त और चतुर्भुज आदि पदों के बारे में जानकारी होनी चाहिए। आवश्यक पदों
की परिभाषाएँ नीचे दी गई हैं:
(i) समान्तर रेखाएँ:
एक तल में दो रेखाएँ l और m समान्तर कहलाती हैं, यदि उनका कोई उभयनिष्ठ बिंदु न हो और हम उन्हें l ॥ m लिखते हैं।
(ii) लंबवत रेखाएँ:
एक ही तल में स्थित दो रेखाएँ p और q लंबवत कहलाती हैं यदि वे समकोण बनाती हैं और हम उन्हें p ⊥ q के रूप में लिखते हैं।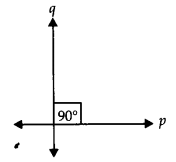
(iii) वृत्त की त्रिज्या:
केंद्र से वृत्त पर स्थित किसी बिंदु की दूरी को वृत्त की त्रिज्या कहते हैं। आकृति में, P केंद्र है और Q वृत्त पर स्थित एक बिंदु है, तो PQ त्रिज्या है।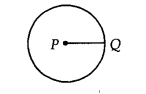
(iv) वर्ग:
एक चतुर्भुज जिसके चारों कोण समकोण हों और चारों भुजाएँ बराबर हों, वर्ग कहलाता है। दी गई आकृति में, PQRS एक वर्ग है।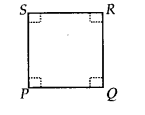
प्रश्न 3.
नीचे दी गई दो 'अभिधारणाओं' पर विचार करें
(i) कोई दो भिन्न बिंदु A और B दिए होने पर, एक तीसरा बिंदु C विद्यमान है जो A और B के बीच में है।
(ii) कम से कम तीन बिंदु ऐसे विद्यमान हैं जो एक ही रेखा पर नहीं हैं।
क्या इन अभिधारणाओं में कोई अपरिभाषित पद हैं? क्या ये अभिधारणाएँ संगत हैं? क्या ये यूक्लिड की अभिधारणाओं का अनुसरण करती हैं? व्याख्या करें।
समाधान:
हाँ, इन अभिधारणाओं में 'बिंदु और रेखा' जैसे अपरिभाषित पद हैं। साथ ही, ये अभिधारणाएँ संगत हैं क्योंकि ये दो अलग-अलग स्थितियों से निपटती हैं क्योंकि
(i) कहता है कि दो बिंदु A और B दिए गए हैं, उनके बीच की रेखा पर एक बिंदु C स्थित है। जबकि
(ii) कहता है कि, बिंदु A और B दिए गए हैं, आप बिंदु C ले सकते हैं जो A और B से होकर जाने वाली रेखा पर न हो।
नहीं, ये अभिधारणाएँ यूक्लिड की अभिधारणाओं का अनुसरण नहीं करती हैं, हालाँकि वे इस अभिधारणा का अनुसरण करती हैं, "दो अलग-अलग बिंदु दिए गए हैं, एक अद्वितीय रेखा है जो उनके माध्यम से गुजरती है।"
प्रश्न 4.
आकृति में, यदि AC = BD है, तो सिद्ध कीजिए कि AB = CD है।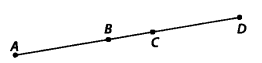
हल:
दिया गया है: AC = BD
⇒ AB + BC = BC + CD
दोनों पक्षों से BC घटाने पर, हम पाते हैं कि
AB + BC – BC = BC + CD – BC
[जब बराबर में से बराबर घटाया जाता है, तो शेषफल बराबर होता है]
⇒ AB = CD
प्रश्न 5.
यूक्लिड के अभिगृहीतों की सूची में अभिगृहीत 5 को 'सार्वभौमिक सत्य' क्यों माना जाता है? (ध्यान दें कि प्रश्न पाँचवीं अभिधारणा के बारे में नहीं है।)
हल:
चूँकि कथन सभी स्थितियों में सत्य है, इसलिए इसे 'सार्वभौमिक सत्य' माना जाता है।
Ex 5.2
प्रश्न 1.
यूक्लिड की पाँचवीं अभिधारणा को आप कैसे पुनः लिखेंगे ताकि इसे समझना आसान हो जाए?
हल:
हम यूक्लिड की पाँचवीं अभिधारणा को इस प्रकार लिख सकते हैं: 'दो भिन्न प्रतिच्छेदी रेखाएँ एक ही रेखा के समांतर नहीं हो सकतीं।'
प्रश्न 2.
क्या यूक्लिड की पाँचवीं अभिधारणा समांतर रेखाओं के अस्तित्व का संकेत देती है? व्याख्या कीजिए।
हल:
हाँ। यदि एक सीधी रेखा l दो रेखाओं m और n पर इस प्रकार पड़ती है कि l के एक ओर के आंतरिक कोणों का योग दो समकोण हैं, तो यूक्लिड की पाँचवीं अभिधारणा के अनुसार, रेखाएँ m और n रेखा l के इस ओर नहीं मिलेंगी। साथ ही, हम जानते हैं कि रेखा l के दूसरी ओर के आंतरिक कोणों का योग भी दो समकोण होंगे। इस प्रकार, वे दूसरी ओर भी नहीं मिलेंगी।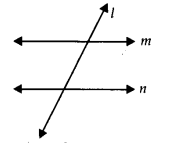
∴ रेखाएँ m और n कभी नहीं मिलती हैं, अर्थात, वे समांतर हैं।
