NCERT Class 9 Maths Chapter 15 प्रायिकता

 NCERT Class 9 Maths Chapter 15 प्रायिकता

NCERT Solutions for Class 9 Maths Chapter 15 प्रायिकता

Ex 15.1

प्रश्न 1.
2 बच्चों वाले 1500 परिवारों को यादृच्छिक रूप से चुना गया, और निम्नलिखित डेटा रिकॉर्ड किया गया।

यादृच्छिक रूप से चुने गए परिवार की संभावना की गणना करें, जिसमें
(i) 2 लड़कियां हों (ii) 1 लड़की हो (iii) कोई लड़की नहीं हो।

साथ ही, जाँच करें कि क्या इन संभावनाओं का योग 1 है।
हल:

प्रश्न 2.
कक्षा IX के एक विशेष सेक्शन में, 40 छात्रों से उनके जन्म के महीने के बारे में पूछा गया और प्राप्त आंकड़ों के लिए निम्नलिखित ग्राफ तैयार किया गया।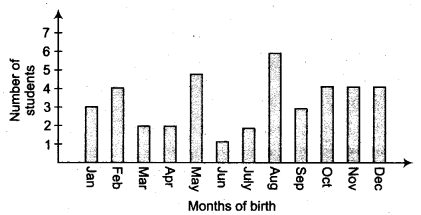

इस कक्षा के एक छात्र के अगस्त में पैदा होने की प्रायिकता ज्ञात कीजिए।
हल:
कक्षा IX में छात्रों की कुल संख्या, n(S) = 40
अगस्त के महीने में जन्मे छात्रों की संख्या, n(E) = 6
कक्षा के छात्रों के अगस्त में पैदा होने की प्रायिकता = \(\frac { n(E) }{ n(S) }\) = \(\frac { 6 }{ 40 }\) = \(\frac { 3 }{ 20 }\)n(E)n(S) = 640 = 320

प्रश्न 3.
तीन सिक्कों को एक साथ 200 बार उछाला जाता है और विभिन्न परिणामों की आवृत्तियाँ निम्नलिखित हैं।

यदि तीनों सिक्कों को एक साथ फिर से उछाला जाता है, तो 2 बार चित्त आने की प्रायिकता ज्ञात कीजिए।
हल:
तीन सिक्कों को उछालने पर, 72 बार चित आने की संभावना है,
अर्थात n(E) = 72।
उछाले गए तीन सिक्कों की कुल संख्या n(S) = 200 है।
∴ 2 बार चित आने की प्रायिकता = \(\frac { n(E) }{ n(S) }\) = \(\frac { 72 }{ 200 }\) = \(\frac { 9 }{ 25 }\)n(E)n(S) = 72200 = 925

प्रश्न 4.
एक संगठन ने 2400 परिवारों को यादृच्छिक रूप से चुना और आय स्तर और परिवार में वाहनों की संख्या के बीच संबंध निर्धारित करने के लिए उनका सर्वेक्षण किया। एकत्र की गई जानकारी नीचे दी गई तालिका में सूचीबद्ध है।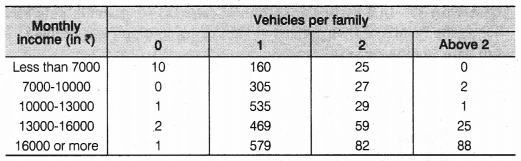

मान लीजिए एक परिवार चुना जाता है। प्रायिकता ज्ञात कीजिए कि चुना गया परिवार
(i) ₹ 10000-13000 प्रति माह कमाता है और उसके पास ठीक 2 वाहन हैं।
(ii) ₹ 16000 या उससे अधिक प्रति माह कमाता है और उसके पास ठीक 1 वाहन है।
(iii) ₹ 7000 प्रति माह से कम कमाता है और उसके पास कोई वाहन नहीं है।
(iv) ₹ 13000-16000 प्रति माह कमाता है और उसके पास 2 से अधिक वाहन हैं।
(v) 1 से अधिक वाहन का मालिक नहीं है।
हल:
संगठन द्वारा चुने गए परिवारों की कुल संख्या, n(S) = 2400
(i) ₹ 10000-13000 प्रति माह कमाने वाले और ठीक 2 वाहन रखने वाले परिवारों की संख्या, n(E 1 ) = 29

(ii) ₹ 16000 या उससे अधिक प्रति माह कमाने वाले और ठीक 1 वाहन रखने वाले परिवारों की संख्या, n(E 2 ) = 579

(iii) ₹ 7000 प्रति माह से कम कमाने वाले और किसी भी वाहन के मालिक नहीं होने वाले परिवारों की संख्या, n(E 3 ) = 10

(iv) ₹ 13000-16000 प्रति माह कमाने वाले और 2 से अधिक वाहन रखने वाले परिवारों की संख्या, n(E 4 ) = 25

(v) 1 से अधिक वाहन न रखने वाले परिवारों की संख्या,
n(E 5 ) = (10 + 1 + 2 + 1) + (160 + 305 + 535 + 469 + 579)
=14 + 2048 = 2062

प्रश्न 5.
एक शिक्षिका 100 अंकों की गणित की परीक्षा में विद्यार्थियों के दो वर्गों के प्रदर्शन का विश्लेषण करना चाहती थी। उनके प्रदर्शन को देखते हुए, उसने पाया कि कुछ विद्यार्थियों को 20 से कम अंक मिले और कुछ को 70 या उससे अधिक अंक मिले। इसलिए उसने उन्हें विभिन्न आकारों के अंतरालों में समूहित करने का निर्णय लिया:
0 – 20, 20 – 30, …, 60 – 70, 70 – 100। फिर उसने निम्नलिखित तालिका बनाई: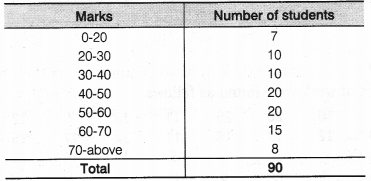

(i) एक विद्यार्थी द्वारा गणित की परीक्षा में 20% से कम अंक प्राप्त करने की प्रायिकता ज्ञात कीजिए।
(ii) एक विद्यार्थी द्वारा 60 या उससे अधिक अंक प्राप्त करने की प्रायिकता ज्ञात कीजिए।
हल:
विद्यार्थियों की कुल संख्या = 90
(i) दी गई तालिका से, 20% से कम अंक प्राप्त करने वाले विद्यार्थियों की संख्या = 7
एक विद्यार्थी द्वारा 20% से कम अंक प्राप्त करने की प्रायिकता =790

(ii) दी गई तालिका से, 60 या उससे अधिक अंक प्राप्त करने वाले विद्यार्थियों की संख्या = [कक्षा-अंतराल 60 – 70 में विद्यार्थियों की संख्या] + [कक्षा-अंतराल 70 – उससे अधिक में विद्यार्थियों की संख्या]
= 15 + 8 = 23
∴ 23 अंक 60 या उससे अधिक अंक प्राप्त करने वाले विद्यार्थी की प्रायिकता =2390

प्रश्न 6.
सांख्यिकी विषय के बारे में विद्यार्थियों की राय जानने के लिए 200 विद्यार्थियों का एक सर्वेक्षण किया गया। आँकड़ों को निम्नलिखित तालिका में दर्ज किया गया है।

इस बात की प्रायिकता ज्ञात कीजिए कि यादृच्छिक रूप से चुने गए एक विद्यार्थी को
(i) सांख्यिकी पसंद है,
(ii) पसंद नहीं है।
हल:
प्राप्त राय वाले विद्यार्थियों की कुल संख्या = 200
(i) ∵ सांख्यिकी पसंद करने वाले विद्यार्थियों की संख्या = 135
∴ सांख्यिकी पसंद करने वाले विद्यार्थी के चयन की प्रायिकता =135200=2740

(ii) ∵ सांख्यिकी पसंद न करने वाले छात्रों की संख्या = 65
∴ सांख्यिकी पसंद न करने वाले छात्र के चयन की प्रायिकता =60200=1340

प्रश्न 7.
40 इंजीनियरों की उनके निवास से उनके कार्यस्थल की दूरी (किमी में) निम्नानुसार पाई गई।

अनुभवजन्य प्रायिकता क्या है कि एक इंजीनियर
(i) अपने कार्यस्थल से 7 किमी से कम दूरी पर रहता है?
(ii) अपने कार्यस्थल से 7 किमी से अधिक या उसके बराबर?
(iii) के भीतर12उसके कार्यस्थल से कितने किलोमीटर दूर है?
हल:
यहाँ, इंजीनियरों की कुल संख्या = 40

(i) ∵ अपने कार्यस्थल से 7 किमी से कम दूरी पर रहने वाले इंजीनियरों की संख्या = 9
∴ अपने कार्यस्थल से 7 किमी से कम दूरी पर रहने वाले इंजीनियर की प्रायिकता =940

(ii) ∵ अपने कार्यस्थल से 7 किमी या उससे अधिक दूरी पर रहने वाले इंजीनियरों की संख्या = 31
∴ एक इंजीनियर की संभावना जो अपने कार्यस्थल से 7 किमी या उससे अधिक दूरी पर रह रही है =3140

(iii) ∵ क्षेत्र में रहने वाले इंजीनियरों की संख्या12अपने कार्यस्थल से किमी दूर = 0
∴ एक इंजीनियर की संभावना जो अपने कार्यस्थल से किमी दूर रह रहा है12उसके कार्यस्थल से किमी =040= 0

प्रश्न 8.
क्रियाकलाप: अपने विद्यालय के गेट के सामने से एक समय अंतराल में गुजरने वाले दोपहिया, तिपहिया और चार पहिया वाहनों की आवृत्ति नोट करें। आपके द्वारा देखे गए कुल वाहनों में से किसी एक वाहन के दोपहिया होने की प्रायिकता ज्ञात कीजिए।
हल:
यह एक क्रियाकलाप है। विद्यार्थी इसे स्वयं कर सकते हैं।

प्रश्न 9.
क्रियाकलाप: अपनी कक्षा के सभी विद्यार्थियों से एक 3-अंकीय संख्या लिखने को कहें। कक्षा से किसी एक विद्यार्थी को यादृच्छिक रूप से चुनें। इसकी क्या प्रायिकता है कि उसके द्वारा लिखी गई संख्या 3 से विभाज्य हो? याद रखें कि एक संख्या 3 से विभाज्य होती है, यदि उसके अंकों का योग 3 से विभाज्य हो।
हल:
विद्यार्थियों के लिए एक कक्षा क्रियाकलाप।

प्रश्न 10.
गेहूं के आटे के ग्यारह बैग, जिनमें से प्रत्येक पर 5 किग्रा अंकित है, में वास्तव में आटे का वजन (किग्रा में) निम्नलिखित है :
4.97, 5.05, 5.08, 5.03, 5.00, 5.06, 5.08, 4.98, 5.04, 5.07, 5.00।
प्रायिकता ज्ञात कीजिए कि इनमें से यादृच्छिक रूप से चुने गए किसी भी बैग में 5 किग्रा से अधिक आटा हो।
हल:
यहाँ, बैगों की कुल संख्या = 11
∵ 5 किग्रा से अधिक आटे वाले बैगों की संख्या = 7
∴ 5 किग्रा से अधिक आटे वाले बैग की प्रायिकता =711

प्रश्न 11.
एक निश्चित शहर की हवा में सल्फर डाइऑक्साइड की सांद्रता प्रति मिलियन (पीपीएम) में पता लगाने के लिए एक अध्ययन किया गया था। 30 दिनों के लिए प्राप्त डेटा इस प्रकार है।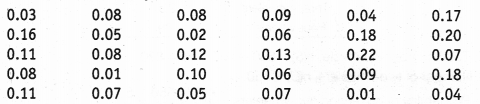

आपको 30 दिनों के लिए एक निश्चित शहर के हवा में सल्फर डाइऑक्साइड की सांद्रता के संबंध में एक आवृत्ति वितरण तालिका तैयार करने के लिए कहा गया था। इस तालिका का उपयोग करके, इनमें से किसी भी दिन 0.12-0.16 अंतराल में सल्फर डाइऑक्साइड की सांद्रता की संभावना का पता लगाएं।
हल:
अब, हम एक आवृत्ति वितरण तालिका तैयार करते हैं।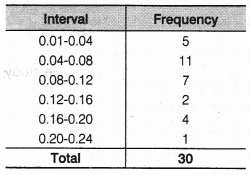

डेटा के लिए दिनों की कुल संख्या, सल्फर डाइऑक्साइड तैयार करने के लिए, n (S) = 30
अंतराल 0.12-0.16 में सल्फर डाइऑक्साइड की आवृत्ति, n (E) = 2