NCERT Class 9 Maths Chapter 14 सांख्यिकी

 NCERT Class 9 Maths Chapter 14 सांख्यिकी

NCERT Solutions for Class 9 Maths Chapter 14 सांख्यिकी

Ex 14.1

प्रश्न 1.
अपने दैनिक जीवन से एकत्रित आँकड़ों के पाँच उदाहरण दीजिए।
हल:
निम्नलिखित पाँच उदाहरण दैनिक जीवन से संबंधित हैं:

• हमारी कक्षा में छात्राओं की संख्या.
• हमारे कंप्यूटर लैब में कंप्यूटर सेटों की संख्या.
• हमारे घर के पिछले दो वर्षों के टेलीफोन बिल।
• समाचार पत्रों से प्राप्त परीक्षा में उपस्थित छात्रों की संख्या।
• शिक्षा विभाग से प्राप्त राज्य के सभी विद्यालयों में महिला शिक्षकों की संख्या।

Ex 14.1 कक्षा 9 गणित प्रश्न 2.
उपरोक्त प्रश्न 1 में दिए गए आँकड़ों को प्राथमिक या द्वितीयक आँकड़ों के रूप में वर्गीकृत करें।
हल:
हमारे पास है,
प्राथमिक आँकड़े: (i), (ii) और (iii)
द्वितीयक आँकड़े: (iv) और (v)

Ex 14.2

प्रश्न 1.
कक्षा VIII के 30 विद्यार्थियों के रक्त समूह निम्नानुसार दर्ज किए गए हैं
A, B, O, O, AB, O, A, O, B, A, O, B, A, O, O,
A, AB, O, A, A, O, O, AB, B, A, O, B, A, B, O
इस आँकड़ों को एक आवृत्ति बंटन सारणी के रूप में निरूपित करें। इन विद्यार्थियों में सबसे सामान्य और सबसे दुर्लभ रक्त समूह कौन सा है?
हल:
आवश्यक आवृत्ति बंटन सारणी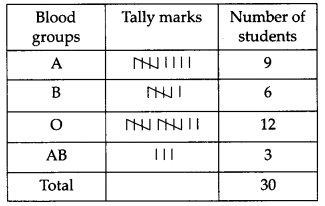

उपरोक्त सारणी से, हमारे पास है सबसे सामान्य रक्त समूह O है। सबसे दुर्लभ रक्त समूह AB है।

प्रश्न 2.
40 इंजीनियरों की उनके निवास से कार्यस्थल तक की दूरी (किमी में) निम्नानुसार पाई गई।

ऊपर दिए गए आँकड़ों के लिए वर्ग माप 5 वाली एक समूहीकृत बारंबारता बंटन सारणी बनाइए, जिसमें पहला अंतराल 0-5 (5 शामिल नहीं) है। इस सारणीबद्ध निरूपण से आपको क्या मुख्य विशेषताएँ दिखाई देती हैं?
हल:
यहाँ, न्यूनतम और अधिकतम मान वाले प्रेक्षण क्रमशः 2 और 32 हैं।
∴ वर्ग अंतराल इस प्रकार हैं:
0 - 5, 5 - 10, 10 - 15, 15 - 20, 20 - 25, 25 - 30, 30 - 35
आवश्यक बारंबारता बंटन सारणी है।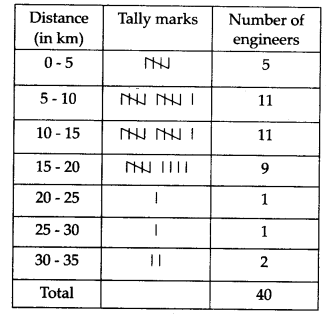

उपरोक्त सारणी से हम देखते हैं कि:
(i) वर्ग अंतराल 5-10 और 10 - 15 की बारंबारताएँ समान हैं, अर्थात प्रत्येक 11 है। यह दर्शाता है कि अधिकतम इंजीनियरों के निवास उनके कार्यस्थल से 5 से 15 किमी दूर हैं।
(ii) वर्ग अंतराल 20 – 25 और 25 – 30 की आवृत्तियाँ भी बराबर हैं, अर्थात् 1-1। इससे पता चलता है कि न्यूनतम संख्या में इंजीनियरों के आवास उनके कार्यस्थल से 20 से 30 किमी दूर हैं।

प्रश्न 3.
30 दिनों के एक महीने के लिए एक निश्चित शहर की सापेक्ष आर्द्रता (% में) निम्नानुसार थी

(i) 84-86, 86-88 आदि वर्गों के साथ एक वर्गीकृत आवृत्ति बंटन सारणी बनाइए।
(ii) आपके विचार से ये आँकड़े किस महीने या ऋतु के बारे में हैं?
(iii) इस आँकड़ों का परिसर क्या है?
हल:
यहाँ, प्रेक्षण का न्यूनतम मान = 84.9
प्रेक्षण का अधिकतम मान = 99.2
अतः, वर्ग अंतराल 84 – 86, 86 – 88, 88 – 90, ……., 98 – 100 हैं।

(i) इस प्रकार, आवश्यक आवृत्ति बंटन सारणी इस प्रकार है: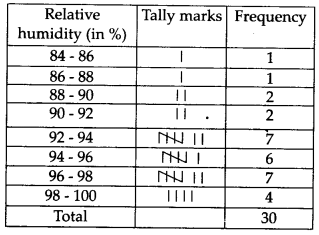

(ii) चूँकि वर्षा ऋतु में सापेक्षिक आर्द्रता अधिक होती है, इसलिए आँकड़े वर्षा ऋतु में लिए गए प्रतीत होते हैं।
(iii) परास = (उच्चतम प्रेक्षण) – (न्यूनतम प्रेक्षण) = 99.2 – 84.9 = 14.3

प्रश्न 4.
निकटतम सेंटीमीटर में मापी गई 50 विद्यार्थियों की लंबाइयाँ निम्नानुसार पाई गई हैं।

(i) ऊपर दिए गए आँकड़ों को एक समूहीकृत बारंबारता बंटन सारणी द्वारा निरूपित कीजिए, वर्ग अंतराल 160 – 165, 165 – 170 आदि लेकर।
(ii) इस सारणी से आप उनकी ऊँचाइयों के बारे में क्या निष्कर्ष निकाल सकते हैं?
हल:
(i) यहाँ, प्रेक्षण का न्यूनतम मान = 150
प्रेक्षण का अधिकतम मान = 173
∴ वर्ग अंतराल 150 – 155, 155 -160, …, 170 – 175 हैं।
अभीष्ट बारंबारता बंटन सारणी है।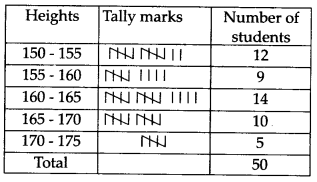

(ii) उपरोक्त सारणी से, हम यह निष्कर्ष निकाल सकते हैं कि 50% से अधिक विद्यार्थी 165 सेमी से छोटे हैं।

प्रश्न 5.
एक निश्चित शहर की हवा में सल्फर डाइऑक्साइड की सांद्रता भाग प्रति मिलियन (ppm) में ज्ञात करने के लिए एक अध्ययन किया गया था। 30 दिनों के लिए प्राप्त आँकड़े इस प्रकार हैं: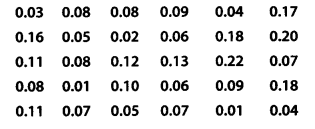

(i) इस आँकड़ों के लिए 0.00 – 0.04, 0.04 – 0.08 इत्यादि वर्ग अंतरालों के साथ एक वर्गीकृत आवृत्ति बंटन सारणी बनाइए।
(ii) कितने दिनों के लिए सल्फर डाइऑक्साइड की सांद्रता 0.11 भाग प्रति मिलियन से अधिक थी?
समाधान:
(i) यहां, अवलोकन का न्यूनतम मान = 0.01
अवलोकन का उच्चतम मान = 0.22
∴ वर्ग अंतराल 0.00 - 0.04, 0.04 - 0.08, ……., 0.20 - 0.24 हैं
आवश्यक आवृत्ति वितरण तालिका है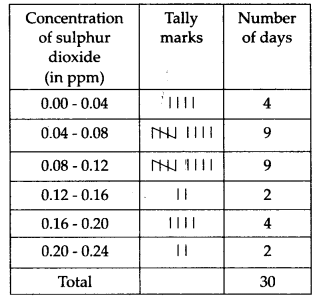

(ii) सल्फर डाइऑक्साइड की सांद्रता 8 दिनों के लिए 0.11 पीपीएम से अधिक थी।

प्रश्न 6.
तीन सिक्कों को एक साथ 30 बार उछाला गया। प्रत्येक बार चित आने की संख्या को निम्न प्रकार लिखा गया।

ऊपर दिए गए आँकड़ों के लिए एक बारंबारता बंटन सारणी बनाइए।
हल:
अभीष्ट बारंबारता बंटन सारणी है: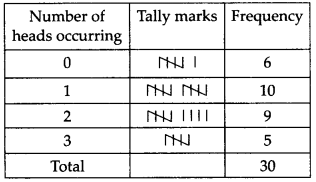

प्रश्न 7.
π का ​​50 दशमलव स्थानों तक मान नीचे दिया गया है
3.14159265358979323846264338327950288419716939937510
(i) दशमलव बिंदु के बाद 0 से 9 तक के अंकों का बारंबारता बंटन बनाइए।
(ii) सबसे अधिक और सबसे कम बार आने वाले अंक कौन से हैं?
हल:
(i) आवश्यक बारंबारता बंटन सारणी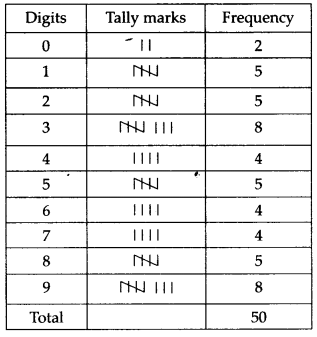

(ii) सबसे अधिक बार आने वाले अंक 3 और 9 हैं तथा सबसे कम बार आने वाला अंक 0 है।

प्रश्न 8.
तीस बच्चों से पूछा गया कि उन्होंने पिछले सप्ताह कितने घंटे टीवी कार्यक्रम देखे।
परिणाम इस प्रकार थे:

(i) इस आँकड़ों के लिए एक समूहीकृत बारंबारता बंटन सारणी बनाइए, वर्ग चौड़ाई 5 और वर्ग अंतरालों में से एक 5 – 10 लीजिए।
(ii) कितने बच्चों ने एक सप्ताह में 15 या अधिक घंटे टेलीविजन देखा?
हल:
(i) यहाँ, प्रेक्षण का न्यूनतम मान = 1 और प्रेक्षण का अधिकतम मान = 17
है। ∴ वर्ग अंतराल 0 – 5, 5 – 10, 15 – 20 हैं।
आवश्यक बारंबारता बंटन सारणी है: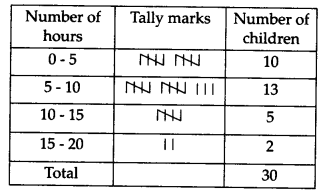

(ii) एक सप्ताह में 15 या अधिक घंटे टेलीविजन देखने वाले बच्चों की संख्या = 2

प्रश्न 9.
एक कंपनी एक विशेष प्रकार की कार बैटरियाँ बनाती है। ऐसी 40 बैटरियों का जीवनकाल (वर्षों में) निम्नानुसार दर्ज किया गया है।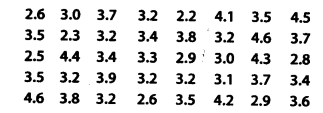

2 – 2.5 के अंतराल से प्रारंभ करते हुए, 0.5 आकार के वर्ग अंतरालों का उपयोग करते हुए, इन आँकड़ों के लिए एक समूहीकृत बारंबारता बंटन सारणी बनाइए।
हल:
यहाँ, प्रेक्षण का न्यूनतम मान = 2.2
और प्रेक्षण का अधिकतम मान = 4.6
है। ∴ वर्ग अंतराल 2.0 – 2.5, 2.5 – 3.0, …., 4.5 – 5.0 हैं।
आवश्यक बारंबारता बंटन सारणी है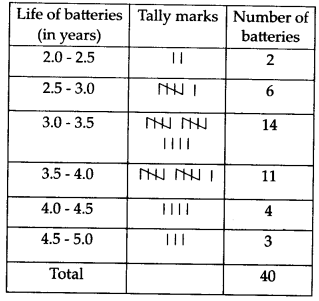

Ex 14.3

प्रश्न 1.
एक संगठन द्वारा विश्व भर में 15-44 वर्ष (वर्षों में) आयु वर्ग की महिलाओं में बीमारी और मृत्यु के कारणों के लिए किए गए सर्वेक्षण में निम्नलिखित आंकड़े (% में) प्राप्त हुए:

(i) ऊपर दी गई जानकारी को आलेखीय रूप में दर्शाइए।
(ii) विश्व भर में महिलाओं के खराब स्वास्थ्य और मृत्यु का प्रमुख कारण कौन सी स्थिति है?

(iii) अपने शिक्षक की सहायता से, ऊपर दिए गए (ii) में दिए गए कारण के प्रमुख कारण में प्रमुख भूमिका निभाने वाले किन्हीं दो कारकों का पता लगाने का प्रयास करें।
हल:
(i) आवश्यक चित्रमय निरूपण इस प्रकार दर्शाया गया है:

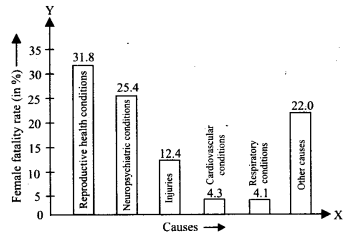
(ii) दुनिया भर में महिलाओं के खराब स्वास्थ्य और मृत्यु का प्रमुख कारण 'प्रजनन स्वास्थ्य स्थितियाँ' हैं।
(iii) दो कारक अशिक्षा और खराब पृष्ठभूमि हो सकते हैं।

प्रश्न 2.
भारतीय समाज के विभिन्न वर्गों में प्रति हजार लड़कों पर लड़कियों की संख्या (निकटतम दहाई तक) के आँकड़े नीचे दिए गए हैं।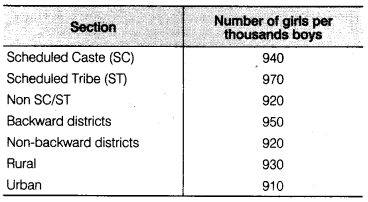

(i) उपरोक्त जानकारी को एक दंड आलेख द्वारा निरूपित कीजिए।
(ii) कक्षा में चर्चा कीजिए कि इस आलेख से क्या निष्कर्ष निकाले जा सकते हैं।
हल:
(i) अभीष्ट दंड आलेख नीचे दर्शाया गया है: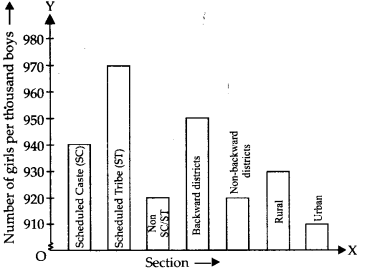

(ii) हम यह निष्कर्ष निकालते हैं कि प्रति हजार लड़कों पर लड़कियों की संख्या अनुसूचित जनजाति वर्ग में अधिकतम है जबकि शहरी वर्ग में न्यूनतम है।

प्रश्न 3.
नीचे एक राज्य विधानसभा चुनाव के मतदान परिणाम में विभिन्न राजनीतिक दलों द्वारा जीती गई सीटें दी गई हैं।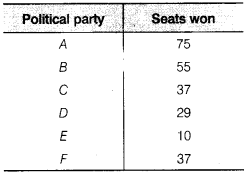

(i) मतदान परिणामों को दर्शाने के लिए एक दंड आलेख खींचिए।
(ii) किस राजनीतिक दल ने अधिकतम सीटें जीतीं?
हल:
(i) आवश्यक दंड आलेख नीचे दर्शाया गया है: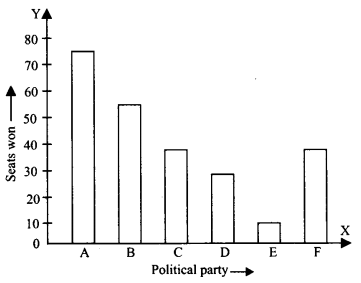

(ii) राजनीतिक दल A ने अधिकतम सीटें जीतीं।

प्रश्न 4.
एक पौधे की 40 पत्तियों की लंबाई एक मिलीमीटर तक मापी गई और प्राप्त आँकड़ों को निम्नलिखित तालिका में दर्शाया गया है।

(i) दिए गए आँकड़ों को दर्शाने के लिए एक आयतचित्र खींचिए।
(ii) क्या समान आँकड़ों के लिए कोई अन्य उपयुक्त आलेखीय निरूपण है?
(iii) क्या यह निष्कर्ष निकालना सही है कि 153 मिमी लंबी पत्तियों की अधिकतम संख्या है और क्यों?
हल:
(i) दी गई बारंबारता बंटन तालिका सतत नहीं है। इसलिए, पहले हमें इसे सतत बंटन में बदलना होगा।

इस प्रकार, संशोधित आवृत्ति वितरण सारणी इस प्रकार है: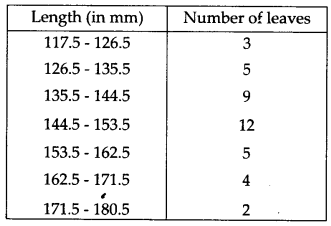

अब, आवृत्ति वितरण का वांछित आयतचित्र नीचे दर्शाया गया है: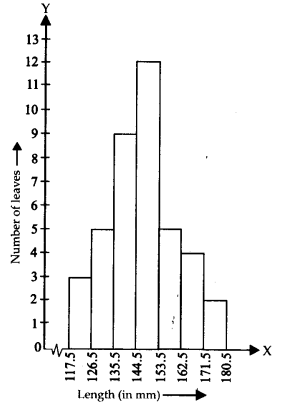

(ii) हाँ, अन्य उपयुक्त आलेखीय निरूपण 'आवृत्ति बहुभुज' है।
(iii) नहीं, यह सही कथन नहीं है। पत्तियों की अधिकतम संख्या वर्ग अंतराल 145 - 153 में होती है।

प्रश्न 5.
निम्नलिखित तालिका 400 निऑन लैंपों का जीवनकाल दर्शाती है।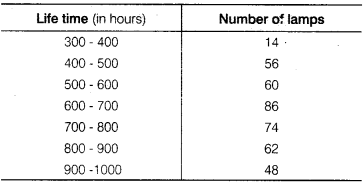

(i) दी गई जानकारी को एक आयतचित्र की सहायता से निरूपित कीजिए।
(ii) कितने लैंपों का जीवनकाल 700 घंटे से अधिक है?
हल:
(i) अभीष्ट आयतचित्र नीचे दर्शाया गया है: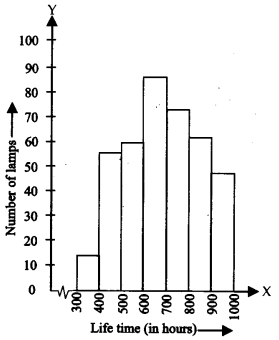

(ii) 700 घंटे से अधिक जीवनकाल वाले लैंपों की संख्या = 74 + 62 + 48 = 184.

प्रश्न 6.
निम्नलिखित तालिका दो सेक्शनों के विद्यार्थियों द्वारा प्राप्त अंकों के अनुसार उनका वितरण दर्शाती है।

दोनों सेक्शनों के विद्यार्थियों के अंकों को एक ही ग्राफ पर दो बारंबारता बहुभुजों द्वारा निरूपित कीजिए। दोनों बहुभुजों से दोनों सेक्शनों के प्रदर्शन की तुलना कीजिए।
हल:
एक बारंबारता बहुभुज बनाने के लिए, हम कक्षा के अंकों को x-अक्ष के अनुदिश अंकित करते हैं। अतः, संशोधित तालिका इस प्रकार है: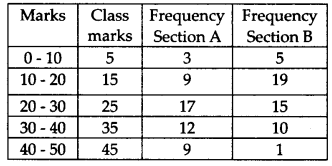

अतः, दो बारंबारता बहुभुज नीचे दर्शाए गए हैं: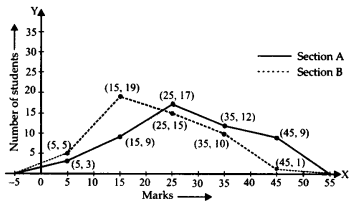

उपरोक्त बारंबारता बहुभुज से, हम देख सकते हैं कि सेक्शन A के अधिक विद्यार्थियों ने अच्छे अंक प्राप्त किए हैं।

प्रश्न 7.
एक क्रिकेट मैच में दो टीमों A और B द्वारा पहली 60 गेंदों पर बनाए गए रन नीचे दिए गए हैं।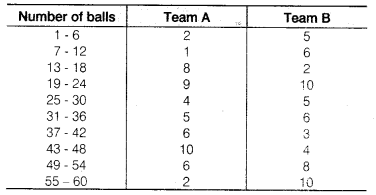

दोनों टीमों के आँकड़ों को एक ही ग्राफ़ पर बारंबारता बहुभुजों द्वारा निरूपित करें।
हल:
दिए गए वर्ग अंतराल सतत नहीं हैं। इसलिए, हम पहले बंटन को सतत रूप में संशोधित करते हैं।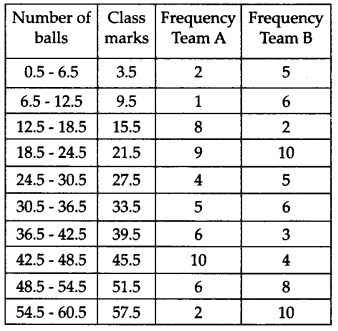

अब, आवश्यक बारंबारता बहुभुज नीचे दर्शाए गए हैं: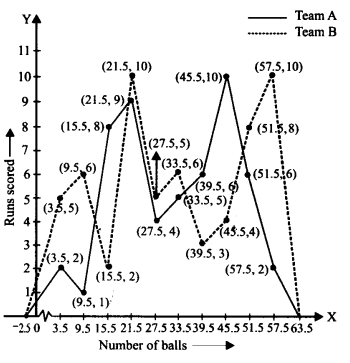

प्रश्न 8.
एक पार्क में खेल रहे विभिन्न आयु वर्ग के बच्चों की संख्या का एक यादृच्छिक सर्वेक्षण निम्नानुसार पाया गया:

उपरोक्त आँकड़ों को दर्शाने के लिए एक आयतचित्र खींचिए।
हल:
यहाँ, कक्षाओं के आकार अलग-अलग हैं। इसलिए, हम प्रत्येक आयत के संगत समायोजित आवृत्तियों, अर्थात् आयत की लंबाई, की गणना करते हैं।
आयत की समायोजित आवृत्ति या लंबाई

यहाँ, न्यूनतम कक्षा का आकार = 2 – 1 = 1
∴ आयतों की समायोजित आवृत्तियों या लंबाई के लिए हमारे पास निम्नलिखित तालिका है: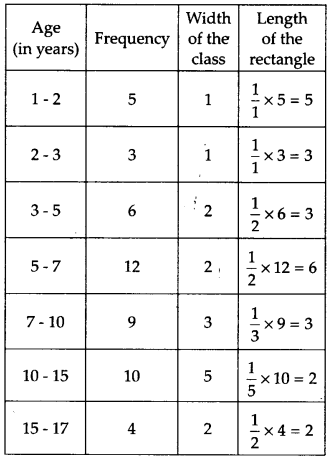

अब, आवश्यक आयतचित्र नीचे दिखाया गया है: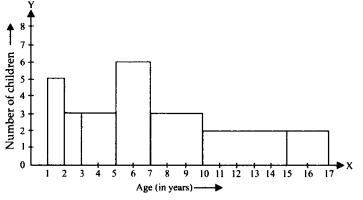

प्रश्न 9.
100 उपनामों को स्थानीय टेलीफोन निर्देशिका से यादृच्छिक रूप से उठाया गया था और उपनामों में अंग्रेजी वर्णमाला के अक्षरों की संख्या का आवृत्ति वितरण निम्नानुसार पाया गया था

(i) दी गई जानकारी को दर्शाने के लिए एक आयत चित्र बनाएं।
(ii) उस वर्ग अंतराल को लिखें जिसमें उपनामों की अधिकतम संख्या स्थित है।
हल:
(i) चूंकि, दिए गए आवृत्ति वितरण के वर्ग अंतराल असमान हैं, और न्यूनतम वर्ग आकार = 6 - 4 = 2।
इसलिए, हमारे पास आयतों की लंबाई के लिए निम्नलिखित तालिका है।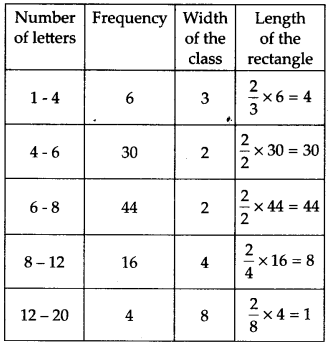

आवश्यक आयत चित्र नीचे दिखाया गया है: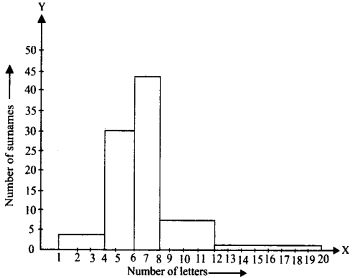

(ii) अधिकतम आवृत्ति 44 है, जो वर्ग अंतराल 6 - 8 के अनुरूप है।
∴ उपनामों की अधिकतम संख्या वर्ग अंतराल 6 - 8 में स्थित है।

Ex 14.4

प्रश्न 1.
10 मैचों की एक श्रृंखला में एक टीम द्वारा निम्नलिखित गोल किए गए:
2, 3, 4, 5, 0, 1, 3, 3, 4, 3.
इन स्कोरों का माध्य, माध्यिका और बहुलक ज्ञात कीजिए।
हल:
माध्य ज्ञात करने के लिए:
यहाँ, n = 10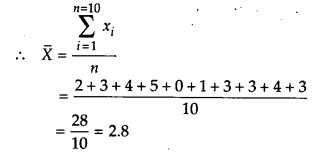

अत: माध्य = 2.8

माध्यिका ज्ञात करने के लिए:
अब दिए गए डेटा को आरोही क्रम में व्यवस्थित करने पर,
हमारे पास है 0,1, 2, 3, 3, 3, 3, 4, 4, 5
∵ n = 10, एक सम संख्या

इस प्रकार, माध्यिका = 3

बहुलक ज्ञात करने के लिए:
दिए गए आँकड़ों में, प्रेक्षण 3, 4 बार,
अर्थात् अधिकतम बार आया है।
अतः बहुलक = 3

प्रश्न 2.
15 विद्यार्थियों को दी गई एक गणित की परीक्षा में, निम्नलिखित अंक (100 में से) दर्ज किए गए हैं:
41, 39, 48, 52, 46, 62, 54, 40, 96, 52, 98, 40, 42, 52, 60
इन आँकड़ों का माध्य, माध्यिका और बहुलक ज्ञात कीजिए।
हल:
माध्य ज्ञात करने के लिए:
यहाँ, n = 15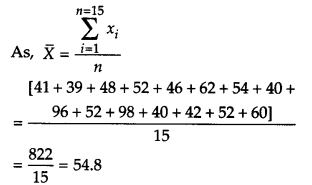

अतः, माध्य = 54.8

माध्यिका ज्ञात करने के लिए:
दिए गए डेटा को आरोही क्रम में व्यवस्थित करने पर,
हमारे पास हैं
39, 40, 40, 41, 42, 46, 48, 52, 52, 52, 54, 60, 62, 96, 98
∵ n = 15, एक विषम संख्या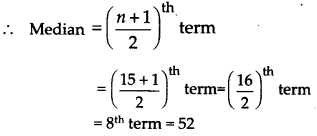

इस प्रकार, माध्यिका = 52

बहुलक ज्ञात करने के लिए:
दिए गए आँकड़ों में, प्रेक्षण 52 तीन बार आया है,
अर्थात् अधिकतम बार।
अतः बहुलक = 52

प्रश्न 3.
निम्नलिखित प्रेक्षणों को आरोही क्रम में व्यवस्थित किया गया है। यदि आँकड़ों की माध्यिका 63 है, तो x का मान ज्ञात कीजिए।
29, 32, 48, 50, x, x + 2, 72, 78, 84, 95
हल:
यहाँ, दिए गए प्रेक्षण आरोही क्रम में हैं।
क्योंकि, n = 10 (एक सम संख्या)

चूँकि, माध्यिका = 63 [दिया है]
∵ x + 1 = 63 ⇒ x = 63 – 1 = 62
इस प्रकार, x का अभीष्ट मान 62 है।

प्रश्न 4.
14, 25,14, 28,18,17,18,14, 23, 22,14 और 18 का बहुलक ज्ञात कीजिए।
हल:
दिए गए आँकड़ों को आरोही क्रम में व्यवस्थित करने पर, हमें 14, 14, 14, 14, 17, 18, 18, 18, 22, 23 25, 28 प्राप्त होते हैं।
चूँकि प्रेक्षण 14 सबसे अधिक बार आ रहा है (अर्थात 4 बार)
∴ दिए गए आँकड़ों का बहुलक = 14

प्रश्न 5.
निम्नलिखित तालिका से एक कारखाने के 60 श्रमिकों का माध्य वेतन ज्ञात कीजिए।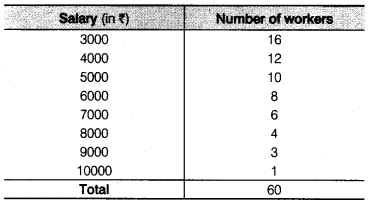

हल: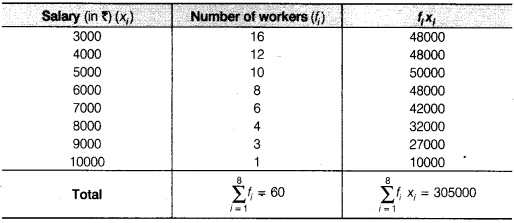

इस प्रकार, अभीष्ट माध्य वेतन = 5083.33 रुपये

प्रश्न 6.
ऐसी स्थिति का एक उदाहरण दीजिए जिसमें
(i) माध्य केन्द्रीय प्रवृत्ति का एक उपयुक्त माप है।
(ii) माध्य केन्द्रीय प्रवृत्ति का एक उपयुक्त माप नहीं है, परन्तु माध्यिका केन्द्रीय प्रवृत्ति का एक उपयुक्त माप है।
हल:
(i) एक कक्षा के विद्यार्थियों की माध्य ऊँचाई।
(ii) एक पेन, एक पुस्तक, एक रबर बैंड, एक माचिस की डिब्बी और एक कुर्सी का माध्यिका भार।