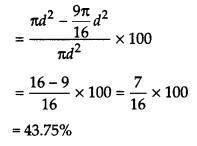NCERT Class 9 Maths Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन

 NCERT Class 9 Maths Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन

NCERT Solutions for Class 9 Maths Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन

Ex 13.1

प्रश्न 1.
1.5 मीटर लंबा, 1.25 मीटर चौड़ा और 65 सेमी गहरा एक प्लास्टिक का डिब्बा बनाना है। यह ऊपर से खुला है। प्लास्टिक शीट की मोटाई को नज़रअंदाज़ करते हुए, निर्धारित करें
(i) डिब्बा बनाने के लिए आवश्यक शीट का क्षेत्रफल।
(ii) इसके लिए शीट की लागत, यदि 1 मीटर² माप वाली शीट की लागत ₹20 है।
हल:
(i) यहाँ, लंबाई (l) = 1.5 मीटर, चौड़ाई (b) = 1.25 मीटर
और ऊँचाई (h) = 65 सेमी = \(\frac { 65 }{ 100 }\) मीटर = 0.65 मीटर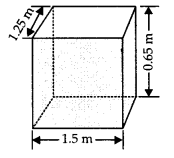65100m = 0.65 m

∵ यह ऊपर से खुला है।
∴ इसका पृष्ठीय क्षेत्रफल
= [पार्श्व पृष्ठीय क्षेत्रफल] + [आधार क्षेत्रफल]
= [2(1 + b)h] + [lb]
= [2(1.50 + 1.25)0.65] m 2 + [1.50 x 1.25] m 2
= [2 x 2.75 x 0.65] m 2 + [1.875] m 2
= 3.575 m 2 + 1.875 m 2 = 5.45 m 2
∴ बॉक्स बनाने के लिए आवश्यक शीट का क्षेत्रफल = 5.45 m 2

(ii) 1 मी 2 शीट का मूल्य = 20 रुपये 5.45 मी 2
शीट का मूल्य = (20 x 5.45) रुपये = 109 रुपये अतः, आवश्यक शीट का मूल्य = 109 रुपये

Ex 13.1 कक्षा 9 गणित प्रश्न 2.
एक कमरे की लंबाई, चौड़ाई और ऊँचाई क्रमशः 5 मीटर, 4 मीटर और 3 मीटर है। कमरे की दीवारों और छत पर 17.50 रुपये प्रति वर्ग मीटर की दर से सफेदी कराने का व्यय ज्ञात कीजिए। हल :
कमरे
की लंबाई (l) = 5 मीटर
कमरे की चौड़ाई (b) = 4 मीटर
कमरे की ऊँचाई (h) = 3 मीटर
कमरा एक घनाभ के समान है जिसकी चारों दीवारों (पार्श्व सतह) और छत पर सफेदी कराई जानी है।
∴ सफेदी कराने का क्षेत्रफल
= [पार्श्व सतह क्षेत्रफल] + [छत का क्षेत्रफल]
= [2(l + b)h] + [lxb]
= [2(5 + 4) x 3] वर्ग मीटर + [5 x 4] वर्ग मीटर = 54 वर्ग मीटर + 20 वर्ग मीटर = 74 वर्ग मीटर 1
वर्ग मीटर क्षेत्रफल पर सफेदी कराने का व्यय = 7.50 रुपये

∴ 74 वर्ग मीटर क्षेत्रफल के लिए सफेदी की लागत = (7.50 x 74) = 555 रुपये

अतः, सफेदी की आवश्यक लागत = 555 रुपये

प्रश्न 3.
एक आयताकार हॉल के फर्श का परिमाप 250 मीटर है। यदि चारों दीवारों को ₹10 प्रति वर्ग मीटर की दर से रंगने की लागत ₹ 15000 है, तो हॉल की ऊँचाई ज्ञात कीजिए।
[संकेत: चारों दीवारों का क्षेत्रफल = पार्श्व पृष्ठीय क्षेत्रफल]
हल:
मान लीजिए आयताकार हॉल की लंबाई = l, चौड़ाई = b, ऊँचाई = h है।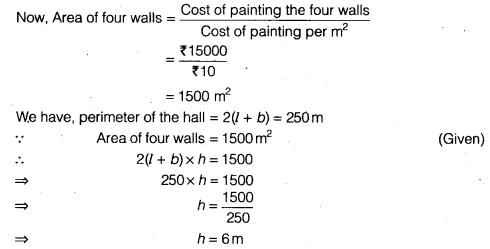

अतः, हॉल की ऊँचाई 6 मीटर है।

प्रश्न 4.
एक निश्चित कंटेनर में मौजूद पेंट 9.375 वर्ग मीटर के बराबर क्षेत्र को पेंट करने के लिए पर्याप्त है । इस कंटेनर से 22.5 सेमी x 10 सेमी x 7.5 सेमी आयाम वाली कितनी ईंटें पेंट की जा सकती हैं?
हल:
दिया गया है, एक ईंट के आयाम
l = 22.5 सेमी, b = 10 सेमी
और b = 7.5 सेमी
ईंटों का कुल पृष्ठीय क्षेत्रफल = 2 (lxb + bxh + hxl)
= 2(22.5 x 10 + 10 x 75 + 75 x 225)
= 2(225 + 75 + 168.75)
= 2 x 468.75 सेमी 2
= 9375 सेमी 2

इस कंटेनर से पेंट की गई ईंटों की संख्या

प्रश्न 5.
एक घनाकार डिब्बे का प्रत्येक किनारा 10 सेमी है और एक अन्य घनाभाकार डिब्बा 12.5 सेमी लंबा, 10 सेमी चौड़ा और 8 सेमी ऊँचा है।
(i) किस डिब्बे का पार्श्व पृष्ठीय क्षेत्रफल अधिक है और कितना अधिक है?
(ii) किस डिब्बे का कुल पृष्ठीय क्षेत्रफल कम है और कितना अधिक है?
समाधान:
किनारे (a) = 10 सेमी वाले घनाकार बॉक्स के लिए
पार्श्व सतह क्षेत्र = 4a 2 = 4 x 10 2 सेमी 2
= 400 सेमी 2
कुल सतह क्षेत्र = 6a 2 = 6 x 10 2 सेमी 2
= 600 सेमी 2
आयामों के साथ घनाभ बॉक्स के लिए,
लंबाई (l) = 12.5 सेमी,
चौड़ाई (b) = 10 सेमी,
ऊंचाई (h) = 8 सेमी
∴ पार्श्व सतह क्षेत्र = 2[l + b] xh = 2[12.5 + 10] x 8 सेमी 2 = 360 सेमी 2
कुल सतह क्षेत्र = 2[lb + bh + hl]
= 2[(12.5 x 10) + (10 x 8) + (8 x 12.5)] सेमी 2
= 2[125 + 80 + 100] सेमी 2
= 2[305] सेमी 2
= 610 सेमी 2
(i) एक घनाकार बॉक्स का पार्श्व पृष्ठीय क्षेत्रफल (400 – 360) सेमी 2 = 40 सेमी 2 अधिक है । (ii) एक घनाकार बॉक्स का कुल पृष्ठीय क्षेत्रफल घनाभ बॉक्स से (610 – 600) सेमी 2 = 10 सेमी 2
छोटा है ।

प्रश्न 6.
एक छोटा सा इनडोर ग्रीनहाउस (हर्बेरियम) पूरी तरह से काँच के शीशों (आधार सहित) से बना है, जिन्हें टेप से एक साथ जोड़ा गया है। यह 30 सेमी लंबा, 25 सेमी चौड़ा और 25 सेमी ऊँचा है।
(i) काँच का क्षेत्रफल क्या है? (
ii) सभी 12 किनारों के लिए कितने टेप की आवश्यकता है?
हल:
हर्बेरियम एक घनाभ जैसा है।
यहाँ, लंबाई (l) = 30 सेमी,
चौड़ाई (b) = 25 सेमी,
ऊँचाई (h) = 25 सेमी
(i) हर्बेरियम (ग्लास) का पृष्ठीय क्षेत्रफल
= 2[lb + bh + hl]
= 2[(30 x 25) + (25 x 25) + (25 x 30)] सेमी 2 – 2[750 + 625 + 750] सेमी 2
= 2[2125] सेमी 2
= 4250 सेमी 2
इस प्रकार, ग्लास का आवश्यक क्षेत्रफल = 4250 सेमी 2

(ii) 12 किनारों की कुल लंबाई = 4l + 4b + 4h
= 4(l + b + h)
= 4(30 + 25 + 25) सेमी
= 4 x 80 सेमी = 320 सेमी
इस प्रकार, टेप की आवश्यक लंबाई = 320 सेमी

प्रश्न 7.
परवीन अपनी कार के लिए एक अस्थायी आश्रय बनाना चाहती थी। वह तिरपाल से एक बॉक्सनुमा संरचना बनाना चाहती थी जो कार के चारों ओर और ऊपरी भाग को ढके (सामने का भाग एक फ्लैप की तरह हो जिसे लपेटा जा सके)। यह मानते हुए कि सिलाई के किनारे बहुत छोटे और इसलिए नगण्य हैं, 2.5 मीटर ऊँचाई और 4 मीटर x 3 मीटर आधार विमाओं वाले इस आश्रय को बनाने के लिए कितने तिरपाल की आवश्यकता होगी?
हल:
यहाँ, लंबाई (l) = 4 मीटर,
चौड़ाई (b) = 3 मीटर
और ऊँचाई (h) = 2.5 मीटर
है। संरचना एक घनाभ के समान है।
∴ आधार को छोड़कर घनाभ का पृष्ठीय क्षेत्रफल
= [पार्श्व पृष्ठीय क्षेत्रफल] + [छत का क्षेत्रफल]
= [2(l + b)h] + [lb]
= [2(4 + 3) x 2.5] m 2 + [4 x 3] m 2
= 35 m 2 + 12 m 2 = 47 m 2
इस प्रकार, 47 m 2 तिरपाल की आवश्यकता होगी।

Ex 13.2

प्रश्न 1.
14 सेमी ऊँचाई वाले एक लम्बवृत्तीय बेलन का वक्र पृष्ठीय क्षेत्रफल 88 सेमी 2 है । बेलन के आधार का व्यास ज्ञात कीजिए।
हल:
मान लीजिए r बेलन की त्रिज्या है।
यहाँ, ऊँचाई (h) = 14 सेमी और वक्र पृष्ठीय क्षेत्रफल = 88 सेमी 2
बेलन का वक्र पृष्ठीय क्षेत्रफल = 2πrh
⇒ 2πrh = 88
⇒ 2 x227xrx 14 = 88
⇒ r =88 × 72 × 22 × 14= 1 सेमी
∴ व्यास = 2 x r = (2 x 1) सेमी = 2 सेमी

प्रश्न 2.
एक धातु की चादर से 1 मीटर ऊँचाई और 140 सेमी आधार व्यास वाला एक बंद बेलनाकार टैंक बनाना है। इसके लिए कितने वर्ग मीटर चादर की आवश्यकता होगी?
हल:
यहाँ, ऊँचाई (h) = 1 मीटर
आधार का व्यास = 140 सेमी = 1.40 मीटर
त्रिज्या (r) =1.402m = 0.70 m
बेलन का कुल पृष्ठीय क्षेत्रफल = 2πr (h + r)
= 2 x227x 0.70(1 + 0.70)मी 2
= 2 x 22 x 0.10 x 1.70 मी 2
= 2 x 22 x10100एक्स170100एम 2
=748100मी 2 = 7.48 मी 2
अतः, आवश्यक शीट = 7.48 मी 2

प्रश्न 3.
एक धातु का पाइप 77 सेमी लंबा है। अनुप्रस्थ काट का आंतरिक व्यास 4 सेमी और बाहरी व्यास 4.4 सेमी है (चित्र देखें)। इसका
(i) आंतरिक वक्र पृष्ठीय क्षेत्रफल
(ii) बाहरी वक्र पृष्ठीय क्षेत्रफल
(iii) कुल पृष्ठीय क्षेत्रफल ज्ञात कीजिए।

हल:
धातु के पाइप की लंबाई = 77 सेमी।
यह एक बेलन के आकार का है।
∴ बेलन की ऊँचाई (h) = 77 सेमी।
आंतरिक व्यास = 4 सेमी।
आंतरिक त्रिज्या (r) =42सेमी = 2 सेमी
बाहरी व्यास = 4.4 सेमी
⇒ बाहरी त्रिज्या (R) =4.42सेमी = 2.2 सेमी

(i) आंतरिक वक्र पृष्ठीय क्षेत्रफल = 2πrh
= 2 x227x 2 x 77 सेमी 2
= 2 x 22 x 2 x 11 सेमी 2 = 968 सेमी 2

(ii) बाहरी वक्र पृष्ठीय क्षेत्रफल = 2πRh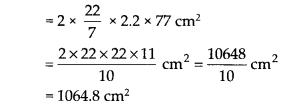

(iii)कुल पृष्ठीय क्षेत्रफल = [आंतरिक वक्र पृष्ठीय क्षेत्रफल] + [बाहरी वक्र पृष्ठीय क्षेत्रफल] + [दो वृत्ताकार सिरों का क्षेत्रफल]
= [2πrh] + [2πRh] + 2[π(R 2 – r 2 )]
= [968 सेमी 2 ] + [1064.8 सेमी 2 ]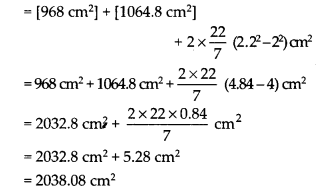

प्रश्न 4.
एक रोलर का व्यास 84 सेमी और लंबाई 120 सेमी है। एक खेल के मैदान को समतल करने के लिए इसे एक बार घूमने में 500 पूर्ण चक्कर लगाने पड़ते हैं। खेल के मैदान का क्षेत्रफल वर्ग मीटर में ज्ञात कीजिए । हल
:
रोलर एक बेलन के आकार का है जिसका व्यास = 84 सेमी है
⇒ रोलर की त्रिज्या (r) =842सेमी = 42 सेमी
रोलर की लंबाई (h) = 120 सेमी
रोलर का वक्र पृष्ठीय क्षेत्रफल = 2πrh
= 2 x227x 42 x 120 सेमी 2
= 2 x 22 x 6 x 120 सेमी 2 = 31680 सेमी 2
अब, रोलर के एक चक्कर में समतल किए गए खेल के मैदान का क्षेत्रफल = 31680cm 2
=3168010000m 2
∴ 500
चक्करों में समतल किए गए खेल के मैदान का क्षेत्रफल = 500 x3168010000m 2 = 1584m 2

प्रश्न 5.
एक लंब वृत्तीय बेलन का वक्र पृष्ठीय क्षेत्रफल 4.4 m2 है। यदि बेलन के आधार की त्रिज्या 0.7 m है, तो इसकी ऊँचाई ज्ञात कीजिए। एक लंब वृत्तीय बेलन का वक्र पृष्ठीय क्षेत्रफल 4.4 m2 है। यदि बेलन के आधार की त्रिज्या 0.7 m है, तो इसकी ऊँचाई ज्ञात कीजिए।
हल:
त्रिज्या (r) = 0.7 m
मान लीजिए बेलन की ऊँचाई hm है।
बेलन का वक्र पृष्ठीय क्षेत्रफल = 2πrh
= 2 x227x710x hm 2
लेकिन वक्र पृष्ठीय क्षेत्रफल 4.4 m 2 है । [दिया गया है]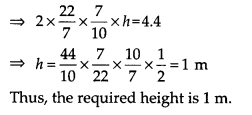

प्रश्न 6.
एक गर्म जल तापन प्रणाली में, 28 मीटर लंबाई और 5 सेमी व्यास वाला एक बेलनाकार पाइप है। प्रणाली में कुल विकिरण पृष्ठ ज्ञात कीजिए।
हल:
USD बेलनाकार पाइप की लंबाई (h) = 28 मीटर
पाइप का व्यास = 5 सेमी
∴ त्रिज्या (r) =52cm =5200m
बेलन का वक्र पृष्ठीय क्षेत्रफल = 2πrh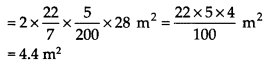

इस प्रकार, कुल विकिरण सतह 4.4 m 2 है ।

प्रश्न 7.
आकृति में, आप एक लैंपशेड का फ्रेम देख रहे हैं। इसे एक सजावटी कपड़े से ढकना है। फ्रेम का आधार व्यास 20 सेमी और ऊँचाई 30 सेमी है। फ्रेम के ऊपर और नीचे इसे मोड़ने के लिए 2.5 सेमी का मार्जिन दिया जाना है। लैंपशेड को ढकने के लिए कितने कपड़े की आवश्यकता होगी, यह ज्ञात कीजिए।

हल:
लैंपशेड एक बेलन के आकार का है,
जहाँ त्रिज्या (r) =202सेमी = 10 सेमी
और ऊंचाई = 30 सेमी।
फ्रेम के ऊपर और नीचे 2.5 सेमी का मार्जिन जोड़ा जाना है।
∴ बेलन की कुल ऊंचाई, (h)
= 30 सेमी + 2.5 सेमी + 2.5 सेमी = 35 सेमी
अब, वक्र पृष्ठीय क्षेत्रफल = 2πrh
= 2 x227x 10 x 35 सेमी 2
= 2200 सेमी 2
इस प्रकार, कपड़े का आवश्यक क्षेत्रफल = 2200 सेमी 2

प्रश्न 8.
एक विद्यालय के विद्यार्थियों को कार्डबोर्ड का उपयोग करके आधार वाले बेलन के आकार के पेनहोल्डर बनाने और सजाने की प्रतियोगिता में भाग लेने के लिए कहा गया था। प्रत्येक पेनहोल्डर की त्रिज्या 3 सेमी और ऊंचाई 10.5 सेमी होनी थी। विद्यालय को प्रतियोगियों को कार्डबोर्ड उपलब्ध कराना था। यदि 35 प्रतियोगी थे, तो प्रतियोगिता के लिए कितना कार्डबोर्ड खरीदना आवश्यक था?
हल:
यहाँ, पेनहोल्डर बेलन के आकार के हैं।
पेनहोल्डर की त्रिज्या (r) = 3 सेमी
पेनहोल्डर की ऊँचाई (h) = 10.5 सेमी
चूँकि, पेनहोल्डर ऊपर से खुला होना चाहिए।
अब, पेनहोल्डर का पृष्ठीय क्षेत्रफल = [पार्श्व पृष्ठीय क्षेत्रफल] + [आधार क्षेत्रफल]
= [2πrh] + [πr 2 ]

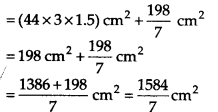
∴ 35 पेनहोल्डरों का पृष्ठीय क्षेत्रफल
= 35 x15847सेमी 2 = 7920 सेमी 2
इस प्रकार, 7920 सेमी 2 कार्डबोर्ड खरीदने की आवश्यकता थी।

Ex 13.3

प्रश्न 1.
एक शंकु के आधार का व्यास 10.5 सेमी है और इसकी तिर्यक ऊँचाई 10 सेमी है। इसका वक्र पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हल:
यहाँ, आधार का व्यास = 10.5 सेमी
⇒ त्रिज्या (r) =10.52सेमी
और तिर्यक ऊँचाई (l) =10 सेमी
शंकु का वक्र पृष्ठीय क्षेत्रफल = πrl
=227x10.52x 10सेमी 2
= 11 x 15 x 1 सेमी 2 = 165सेमी 2

प्रश्न 2.
एक शंकु का सम्पूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए, यदि इसकी तिर्यक ऊँचाई 21 मीटर और आधार का व्यास 24 मीटर है।
हल:
यहाँ, व्यास = 24 मीटर 24
∴ त्रिज्या (r) =242m = 12 m
और तिर्यक ऊँचाई (l) = 21 m
∴ शंकु का कुल पृष्ठीय क्षेत्रफल = πr(r +1)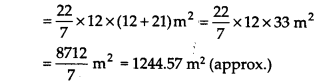

प्रश्न 3.
एक शंकु का वक्र पृष्ठीय क्षेत्रफल 308 वर्ग सेमी है और इसकी तिर्यक ऊँचाई 14 सेमी है।
(i) आधार की त्रिज्या और
(ii) शंकु का कुल पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हल:
यहाँ, वक्र पृष्ठीय क्षेत्रफल = πrl = 308 सेमी² तिर्यक
ऊँचाई (l) = 14 सेमी

(i) माना आधार की त्रिज्या 'r' सेमी है
∴ πrl = 308 ⇒227xrx 14 = 308
r =308 × 722 × 14= 7 सेमी.
अतः शंकु की त्रिज्या 7 सेमी. है।

(ii) आधार क्षेत्रफल = πr 2 =227x 7 2 सेमी 2
= 22 x 7 सेमी 2 = 154 सेमी 2
और वक्र पृष्ठीय क्षेत्रफल = 308 सेमी 2 [दिया गया है]
∴ शंकु का कुल पृष्ठीय क्षेत्रफल
= [वक्र पृष्ठीय क्षेत्रफल] + [आधार क्षेत्रफल] = 308 सेमी 2 + 154 सेमी 2
= 462 सेमी 2

प्रश्न 4.
8 मीटर ऊँचे और 6 मीटर आधार त्रिज्या वाले शंक्वाकार तंबू बनाने के लिए 3 मीटर चौड़े तिरपाल की कितनी लंबाई की आवश्यकता होगी? मान लीजिए कि किनारों की सिलाई और काटने में लगने वाली सामग्री की अतिरिक्त लंबाई लगभग 20 सेमी है। (π = 3.14 का प्रयोग कीजिए)
हल:
मान लीजिए r, h और l क्रमशः तंबू की त्रिज्या, ऊँचाई और तिर्यक ऊँचाई हैं।

किनारों की सिलाई और काटने के लिए आवश्यक अतिरिक्त सामग्री = 20 सेमी = Q 2 मीटर अतः, आवश्यक तिरपाल की कुल लंबाई = 62.8 + Q 2 = 63 मीटर

प्रश्न 5.
एक शंक्वाकार मकबरे की तिर्यक ऊँचाई और आधार का व्यास क्रमशः 25 मीटर और 14 मीटर है। ₹ 210 प्रति 100 मीटर 2 की दर से इसकी वक्र सतह पर सफेदी कराने का व्यय ज्ञात कीजिए ।
हल:
तिर्यक ऊँचाई l = 25 मीटर
और व्यास = 14 मीटर
∴ त्रिज्या r = 7 मीटर

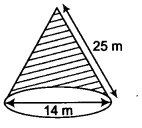
प्रश्न 6.
एक जोकर की टोपी एक लम्बवृत्तीय शंकु के आकार की है जिसकी आधार त्रिज्या 7 सेमी और ऊँचाई 24 सेमी है। ऐसी 10 टोपियाँ बनाने के लिए आवश्यक शीट का क्षेत्रफल ज्ञात कीजिए।
हल: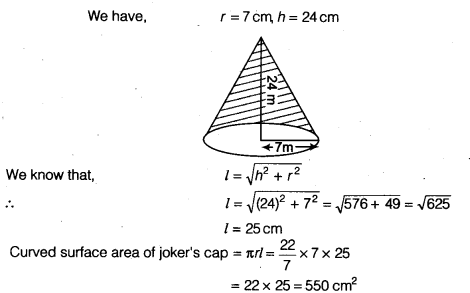

∵ 1 टोपी बनाने के लिए आवश्यक शीट = 550 सेमी 2
∴ 10 टोपियाँ बनाने के लिए आवश्यक शीट = 550 x 10 = 5500 सेमी 2

प्रश्न 7.
एक बस स्टॉप को सड़क के शेष भाग से पुनर्चक्रित कार्डबोर्ड से बने 50 खोखले शंकुओं का उपयोग करके अवरोधित किया गया है। प्रत्येक शंकु का आधार व्यास 40 सेमी और ऊँचाई 1 मीटर है। यदि प्रत्येक शंकु के बाहरी भाग को रंगना है और रंगाई की लागत ₹12 प्रति वर्ग मीटर है, तो इन सभी शंकुओं को रंगने की लागत क्या होगी? (π = 3.14 का प्रयोग करें और104−−−√= 1.02)
हल:
आधार का व्यास = 40 सेमी

= रु. 384.336 = रु. 384.34 (लगभग)
इस प्रकार, पेंटिंग की आवश्यक लागत रु. 384.34 (लगभग) है।

Ex 13.4

प्रश्न 1.
त्रिज्या वाले गोले का पृष्ठीय क्षेत्रफल ज्ञात कीजिए
(i) 10.5 सेमी
(ii) 5.6 सेमी
(iii) 14 सेमी
हल:
(i) यहाँ, r = 10.5 सेमी
गोले का पृष्ठीय क्षेत्रफल = 4πr 2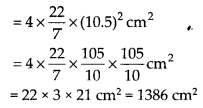

(ii) यहाँ, r = 5.6 सेमी
गोले का पृष्ठीय क्षेत्रफल = 4πr 2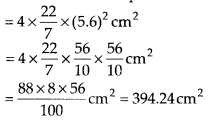

(iii) यहाँ, r = 14 सेमी
गोले का पृष्ठीय क्षेत्रफल = 4πr 2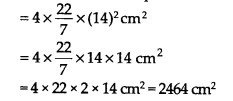

प्रश्न 2.
एक गोले का पृष्ठीय क्षेत्रफल ज्ञात कीजिए जिसका व्यास
(i) 14 सेमी
(ii) 21 सेमी
(iii) 3.5 मीटर है।
हल:
(i) यहाँ, व्यास = 14 सेमी

(ii) यहाँ, व्यास = 21 सेमी

(iii) यहाँ, व्यास = 3.5 मीटर

प्रश्न 3.
10 सेमी त्रिज्या वाले अर्धगोले का कुल पृष्ठीय क्षेत्रफल ज्ञात कीजिए। (π = 3.14 का प्रयोग कीजिए)
हल:
यहाँ, त्रिज्या (r) = 10 सेमी
अर्धगोले का कुल पृष्ठीय क्षेत्रफल = 3πr 2
= 3 x 3.14 x 10 x 10 सेमी 2 = 942 सेमी 2

प्रश्न 4.
एक गोलाकार गुब्बारे की त्रिज्या 7 सेमी से बढ़कर 14 सेमी हो जाती है क्योंकि इसमें हवा भरी जाती है। दोनों स्थितियों में गुब्बारे के पृष्ठीय क्षेत्रफलों का अनुपात ज्ञात कीजिए।
हल:
दोनों स्थितियों में गुब्बारे के पृष्ठीय क्षेत्रफलों का अनुपात ज्ञात कीजिए।
BSD स्थिति I: जब त्रिज्या (r 1 ) = 7 सेमी
पृष्ठीय क्षेत्रफल = 4πr 1 2 = 4 x227x (7) सेमी 2
= 4 x 22 x 7 सेमी 2 = 616 सेमी 2

केस II: जब त्रिज्या (r 2 ) = 14 सेमी 2
पृष्ठीय क्षेत्रफल = 4πr 2 2 =4 x227x (14) 2 सेमी 2
= 4 x 22 x 14 x 2 सेमी 2 = 2464 सेमी 2
∴ आवश्यक अनुपात =6162464=14या 1 : 4

प्रश्न 5.
पीतल से बने एक अर्धगोलाकार कटोरे का आंतरिक व्यास 10.5 सेमी है। ₹16 प्रति 100 वर्ग सेमी की दर से इसके अंदर की ओर टिन-प्लेटिंग की लागत ज्ञात कीजिए।
हल:
अर्धगोलाकार कटोरे का आंतरिक व्यास = 10.5 सेमी

प्रश्न 6.
एक गोले की त्रिज्या ज्ञात कीजिए जिसका पृष्ठीय क्षेत्रफल 154 वर्ग सेमी है।
हल:
मान लीजिए गोले की त्रिज्या r सेमी है।
गोले का पृष्ठीय क्षेत्रफल = 4πr 2
∴ 4πr 2 = 154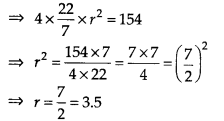

अतः, गोले की अभीष्ट त्रिज्या 3.5 सेमी है।

प्रश्न 7.
चंद्रमा का व्यास पृथ्वी के व्यास का लगभग एक-चौथाई है। उनके पृष्ठीय क्षेत्रफलों का अनुपात ज्ञात कीजिए।
हल:
मान लीजिए पृथ्वी का व्यास = d 1

प्रश्न 8.
एक अर्धगोलाकार कटोरा स्टील से बना है, जिसकी मोटाई 0.25 सेमी है। कटोरे की आंतरिक त्रिज्या 5 सेमी है। कटोरे का बाहरी वक्र पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हल:
आंतरिक त्रिज्या (r) = 5 सेमी
मोटाई = 0.25 सेमी

∴ बाहरी त्रिज्या (R) [5.00 + 0251 सेमी = 5.25 सेमी
∴ कटोरे का बाहरी वक्र पृष्ठीय क्षेत्रफल = 2πR 2

प्रश्न 9.
एक लम्बवृत्तीय बेलन त्रिज्या r वाले एक गोले को घेरे हुए है (चित्र देखें)। ज्ञात कीजिए:
(i) गोले का पृष्ठीय क्षेत्रफल,
(ii) बेलन का वक्र पृष्ठीय क्षेत्रफल,
(iii) (i) और (ii) में प्राप्त क्षेत्रफलों का अनुपात।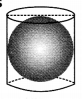

हल:
(i) गोले के लिए, त्रिज्या = r
∴ गोले का पृष्ठीय क्षेत्रफल = 4πR 2

(ii) लम्ब वृत्तीय बेलन के लिए,
बेलन की त्रिज्या = गोले की त्रिज्या
∴ बेलन की त्रिज्या = r
बेलन की ऊँचाई = गोले का व्यास
∴ बेलन की ऊँचाई (h) 2r
चूँकि, बेलन का वक्र पृष्ठीय क्षेत्रफल = 2πrh
= 2πr(2r) = 4πr 2

Ex 13.5

प्रश्न 1.
एक माचिस की डिब्बी का माप 4 सेमी x 2.5 सेमी x 1.5 सेमी है। ऐसी 12 डिब्बियों वाले पैकेट का आयतन क्या होगा?
हल:
चूँकि, माचिस की डिब्बी घनाभ के आकार की होती है।
यहाँ, लंबाई (l) = 4 सेमी, चौड़ाई (b) = 2.5 सेमी
और ऊँचाई (h) = 1.5 सेमी
∴ माचिस की डिब्बी का आयतन = lxbxh
= 4 x 25 x 1.5 सेमी 3
= 4 x2510x1510सेमी 3
= 15 सेमी 3
⇒ ऐसे 12 डिब्बों का आयतन = 12 x 15 सेमी 3
= 180 सेमी 3

प्रश्न 2.
एक घनाभाकार पानी की टंकी 6 मीटर लंबी, 5 मीटर चौड़ी और 4.5 मीटर गहरी है। इसमें कितने लीटर पानी आ सकता है? (1 मीटर 3 = 1000 लीटर)
हल:
लंबाई (l) = 6 मीटर, चौड़ाई (h) = 5 मीटर और
गहराई (h) = 4.5 मीटर
∴ धारिता =lxbxh = 6 x 5 x 4.5 मीटर 3
= 6 x 5 x4510m = 3 x 45m 3 = 135m 3
∵ 1 m 3 = 1000 लीटर
⇒ 135 m 3 = 135000 लीटर
∴ टैंक में पानी की आवश्यक मात्रा = 135000 लीटर।

प्रश्न 3.
एक घनाभाकार बर्तन 10 मीटर लंबा और 8 मीटर चौड़ा है। 380 घन मीटर द्रव रखने के लिए इसे कितना ऊँचा बनाया जाना चाहिए?
हल:
लंबाई (l) = 10 मीटर, चौड़ाई (b) = S m
आयतन (V) = 380 मीटर 3
माना घनाभाकार बर्तन की ऊँचाई 'h' है।
Ex 13.5 कक्षा 9 गणित घनाभाकार बर्तन का आयतन = lxbxh
⇒ 10 x 8 xhm 3 = 80h m 3
⇒ 80h = 380
⇒ h =38080= 4.75 मीटर
इस प्रकार, बर्तन की आवश्यक ऊंचाई = 4.75 मीटर

प्रश्न 4.
₹30 प्रति वर्ग मीटर की दर से 8 मीटर लंबा, 6 मीटर चौड़ा और 3 मीटर गहरा एक घनाभाकार गड्ढा खोदने की लागत ज्ञात कीजिए।
हल:
लंबाई (i) = 8 मीटर
चौड़ाई (b) = 6 मीटर
गहराई (h) = 3 मीटर
∴ घनाभाकार गड्ढे का आयतन = lxbxh
= 8 x 6 x 3 मीटर 3 = 144 मीटर 3
अतः, गड्ढा खोदने की लागत = रु. (144 x 30)
= रु. 4320

प्रश्न 5.
एक घनाभाकार टैंक की धारिता 50000 लीटर पानी की है। टैंक की चौड़ाई ज्ञात कीजिए, यदि इसकी लंबाई और गहराई क्रमशः 2.5 मीटर और 10 मीटर है।
हल:
ira टैंक की लंबाई (l) = 2.5 मीटर
टैंक की गहराई (h) = 10 मीटर
माना टैंक की चौड़ाई b मीटर है।
∴ टैंक का आयतन (धारिता) = lxbxh
= 2.5 xbx 10 m 3
=2510x 10 x bm 3
= 25bm 3
लेकिन टैंक की क्षमता = 50000 लीटर
= 50 m 3 [ ∵ 1000 लीटर = 1 m 3 ]
∴ 25b = 50 ⇒ b =5025= 2
अतः टैंक की चौड़ाई = 2 मीटर

प्रश्न 6.
4000 की आबादी वाले एक गाँव में प्रति व्यक्ति प्रतिदिन 150 लीटर पानी की आवश्यकता होती है। इसमें 20 m x 15 m x 6 m माप का एक टैंक है। इस टैंक का पानी कितने दिनों तक चलेगा?
हल:
fcWra टैंक की लंबाई (l) = 20 m
टैंक की चौड़ाई (b) = 15 m
टैंक की ऊँचाई (h) = 6 m
∴ टैंक का आयतन = lxbxh
= 20 x 15 x 6 m 3 = 1800 m 3
क्योंकि, 1 m 3 = 1000 लीटर
∴ टैंक की क्षमता = 1800 x 1000 लीटर = 1800000 लीटर
क्योंकि, प्रति व्यक्ति प्रतिदिन 150 लीटर पानी की आवश्यकता होती है।
∴ 4000 लोगों द्वारा प्रतिदिन आवश्यक पानी की मात्रा = 150 x 4000 लीटर
मान लीजिए आवश्यक दिनों की संख्या x है
∴ 4000 x 150 xx = 1800000
⇒ x =18000004000 × 150= 3
इस प्रकार, आवश्यक दिनों की संख्या 3 है।

प्रश्न 7.
एक गोदाम का माप 40 m x 25 m x 10 m है। 15 m x 125 m x 0.5 m माप वाले लकड़ी के क्रेटों की अधिकतम संख्या ज्ञात कीजिए जिन्हें गोदाम में रखा जा सकता है।
हल:
गोदाम का आयतन = 40 x 25 x 10 m 3
लकड़ी के क्रेट का आयतन = 1.5 x 1.25 x 0.5 m 3

∴ लकड़ी के क्रेटों की अधिकतम संख्या = 10667.

प्रश्न 8.
12 सेमी भुजा वाले एक ठोस घन को बराबर आयतन वाले आठ घनों में काटा जाता है। नए घन की भुजा क्या होगी? साथ ही, उनके पृष्ठीय क्षेत्रफलों का अनुपात भी ज्ञात कीजिए।
हल:
दिए गए घन की भुजा = 12 सेमी
दिए गए घन का आयतन = (भुजा) 3 = (12)3 cm3
Let the side of the new cube be n
∴ Volume of new cube = n3
⇒ Volume of 8 new cubes = 8n3
According to question,
8n3 = (12)3 = 12 x 12 x 12
⇒ n3 = 12 × 12 × 128  = 6 x 6 x 6
⇒ n 3 = 6 3
⇒ n = 6
इस प्रकार, नए घन की अभीष्ट भुजा 6 सेमी है।
अब, दिए गए घन का पृष्ठीय क्षेत्रफल = 6 x (भुजा) 2 = 6 x 12 2 सेमी 2 = 6 x 12 x 12 सेमी 2
नए घन का पृष्ठीय क्षेत्रफल = 6 x 6 2 सेमी 2
= 6 x 6 x 6 सेमी 2
अब,

इस प्रकार, अभीष्ट अनुपात = 4 : 1

प्रश्न 9.
3 मीटर गहरी और 40 मीटर चौड़ी एक नदी 2 किमी प्रति घंटे की दर से बह रही है। एक मिनट में कितना पानी समुद्र में गिरेगा?
हल:
नदी में बहते पानी को घनाभ के रूप में माना जा सकता है।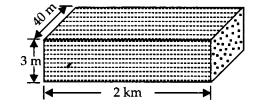

लंबाई (l) = 2 किमी = 2000 मीटर
चौड़ाई (b) = 40 मीटर,
गहराई (h) = 3 मीटर
∴ पानी का आयतन (इस प्रकार बने घनाभ का आयतन) = lxbxh
= 2000 x 40 x 3 मीटर 3
अब, 1 घंटे (60 मिनट) में बहने वाले पानी का आयतन = 2000 x 40 x 3 मीटर 3
1 मिनट में गिरने वाले पानी का आयतन
= [2000 x 40 x 3] + 60 मीटर 3
= 4000 मीटर 3

Ex 13.6

प्रश्न 1.
एक बेलनाकार बर्तन के आधार की परिधि 132 सेमी है और इसकी ऊँचाई 25 सेमी है। इसमें कितने लीटर पानी आ सकता है? (1000 सेमी³ = 1 लीटर)
हल:
माना बेलनाकार बर्तन के आधार की त्रिज्या r सेमी है।
∴ आधार की परिधि = 2πr
⇒ 2πr = 132 [परिधि = 132 सेमी, (दिया है)]
= 2 x227xr = 132
⇒ r =132 x 72 x 22सेमी = 21 सेमी
चूंकि, बर्तन की ऊंचाई (h) = 25 सेमी
बर्तन का आयतन (h) = πr 2 h
=227x (21) 2 x 25सेमी 3
=227x 21 x 21 x 25 सेमी 3
= 22 x 3 x 21 x 25 सेमी 3
= 34650 सेमी 3
∵ बर्तन की धारिता = बर्तन का आयतन
∴ बेलनाकार बर्तन की धारिता = 34650 सेमी 3
चूँकि, 1000 सेमी 3 = 1 लीटर
⇒ 34650 सेमी 3 =346501000लीटर = 34.65 लीटर
इस प्रकार, बर्तन में 34.65 लीटर पानी आ सकता है।

प्रश्न 2.
एक बेलनाकार लकड़ी के पाइप का आंतरिक व्यास 24 सेमी और बाहरी व्यास 28 सेमी है। पाइप की लंबाई 35 सेमी है। यदि 1 सेमी3 लकड़ी का द्रव्यमान 0.6 ग्राम है, तो पाइप का द्रव्यमान ज्ञात कीजिए।
हल:
बेलनाकार पाइप का आंतरिक व्यास = 24 सेमी
⇒ पाइप की आंतरिक त्रिज्या (r) =242सेमी = 12 सेमी
पाइप का बाहरी व्यास = 28 सेमी
पाइप की बाहरी त्रिज्या (आर) = 14 सेमी
पाइप की लंबाई (एच) = 35 सेमी
∴ पाइप में लकड़ी की मात्रा = बाहरी आयतन - आंतरिक आयतन
= πR 2 h - πr 2 h
= πh (R + r) (R - r)
[∵ a2 - b2 = (a + b)(a - b)]
=227 x 35 x (14+12) x (14 – 12)cm3
=22 x 5 x 26 x 2 cm3
Mass of wood in the pipe = (Mass of wood in 1 cm3 of wood) x (Volume of wood in the pipe)
= (0.6g) x (22 x 5 x 26 x 2)cm3
= 610x 22 x 10 x 26 ग्राम = 3432 ग्राम
=34321000किग्रा = 3.432 किग्रा [∵ 1000 ग्राम = 1 किग्रा]
इस प्रकार, पाइप का आवश्यक द्रव्यमान 3.432 किग्रा है।

प्रश्न 3.
यदि किसी बेलन का पार्श्व पृष्ठ 94.2 सेमी² है और उसकी ऊँचाई 5 सेमी है, तो
(i) उसके आधार की त्रिज्या,
(ii) उसका आयतन ज्ञात कीजिए। (π = 3.14 का प्रयोग कीजिए)
हल:
बेलन की ऊँचाई (h) = 5 सेमी
माना बेलन के आधार की त्रिज्या 'r' है।

(i) चूँकि बेलन का पार्श्व पृष्ठीय क्षेत्रफल = 2πrh,
परन्तु बेलन का पार्श्व पृष्ठ 94.2 सेमी 2 है [दिया गया है]
2πrh = 94.2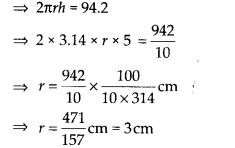

अतः बेलन की त्रिज्या = 3 सेमी

(ii) बेलन का आयतन = πr 2 h
⇒ दिए गए बेलन का आयतन
=3.14 (3) 2 x 5 सेमी 3
=314100x 3 x 3 x 5 सेमी 3
=141310सेमी = 141.3 सेमी 3
अतः, आवश्यक आयतन = 141.3 सेमी 3

प्रश्न 4.
10 मीटर गहरे एक बेलनाकार बर्तन के आंतरिक वक्र पृष्ठ को पेंट करने में ₹2200 का खर्च आता है। यदि पेंटिंग की लागत ₹20 प्रति वर्ग मीटर की दर से है, तो ज्ञात कीजिए:
(i) बर्तन का आंतरिक वक्र पृष्ठीय क्षेत्रफल,
(ii) आधार की त्रिज्या,
(iii) बर्तन की धारिता।
हल:
(i) पेंटिंग की कुल लागत = ₹2200 क्षेत्रफल 12
मीटर की पेंटिंग की लागत = ₹20 कुल लागत ∴ बर्तन का आंतरिक वक्र पृष्ठीय क्षेत्रफल = 110 वर्ग मीटर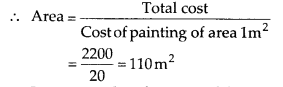

(ii) मान लीजिए r बेलनाकार बर्तन के आधार की त्रिज्या है।
बेलन का वक्र पृष्ठीय क्षेत्रफल = 2πrh

प्रश्न 5.
1 मीटर ऊँचाई वाले एक बंद बेलनाकार बर्तन की धारिता 15.4 लीटर है। इसे बनाने के लिए कितने वर्ग मीटर धातु की शीट की आवश्यकता होगी?
हल:
बेलनाकार बर्तन की धारिता
= 15.4 लीटर = 15.4 x 1000 सेमी 3 [1 लीटर = 10(x) सेमी 3 ]

मान लीजिए rm बर्तन के आधार की त्रिज्या है।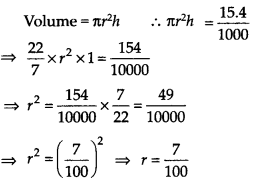

अब, बेलनाकार बर्तन का कुल पृष्ठीय क्षेत्रफल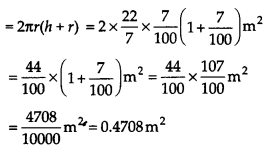

= 0.4708 मी 2 ।

प्रश्न 6.
एक लेड पेंसिल लकड़ी के एक बेलन से बनी है जिसके भीतर ग्रेफाइट का एक ठोस बेलन भरा हुआ है। पेंसिल का व्यास 7 मिमी और ग्रेफाइट का व्यास 1 मिमी है। यदि पेंसिल की लंबाई 14 सेमी है, तो लकड़ी और ग्रेफाइट का आयतन ज्ञात कीजिए।
हल:
चूँकि, 10 मिमी = 1 सेमी:
∴ 1 मिमी =110सेमी
ग्रेफाइट सिलेंडर के लिए,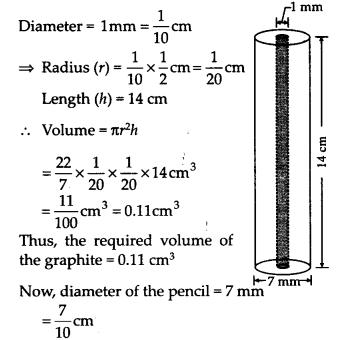

∴ पेंसिल की त्रिज्या (R) =720सेमी
पेंसिल की ऊंचाई (h) = 14 सेमी
पेंसिल का आयतन = πR 2 h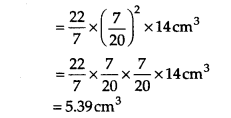

∴ लकड़ी का आयतन = [पेंडिल का आयतन] - [ग्रेफाइट का आयतन]
= 5.39 सेमी 3 - 0.11 सेमी 3
= 5.28 सेमी 3
इस प्रकार, लकड़ी का आवश्यक आयतन = 5.28 सेमी 3 है ।

प्रश्न 7.
एक अस्पताल में एक मरीज को प्रतिदिन 7 सेमी व्यास वाले एक बेलनाकार कटोरे में सूप दिया जाता है। यदि कटोरे को सूप से 4 सेमी ऊँचाई तक भरा जाए, तो 250 मरीजों को परोसने के लिए अस्पताल को प्रतिदिन कितना सूप तैयार करना होगा?
हल:
∵ कटोरा बेलनाकार है, जहाँ आधार का व्यास = 7 सेमी।

इस प्रकार, अस्पताल को 250 मरीजों के लिए प्रतिदिन 38.5 लीटर सूप तैयार करने की आवश्यकता है।

Ex 13.7

प्रश्न 1.
एक लम्ब वृत्तीय शंकु का आयतन ज्ञात कीजिए जिसकी
(i) त्रिज्या 6 सेमी, ऊँचाई 7 सेमी
(ii) त्रिज्या 3.5 सेमी, ऊँचाई 12 सेमी
हल:
(i) यहाँ, शंकु की त्रिज्या (r) = 6 सेमी
ऊँचाई (h) = 7 सेमी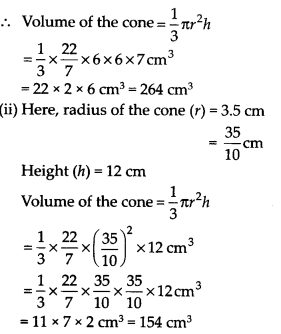

प्रश्न 2.
एक शंक्वाकार बर्तन की लीटर में धारिता ज्ञात कीजिए, जिसकी
(i) त्रिज्या 7 सेमी, तिर्यक ऊँचाई 25 सेमी
(ii) ऊँचाई 12 सेमी, तिर्यक ऊँचाई 13 सेमी है।
हल:
(i) यहाँ, त्रिज्या (r) = 7 सेमी और तिर्यक ऊँचाई (l) = 25 सेमी है।

इस प्रकार, शंक्वाकार बर्तन की अभीष्ट धारिता 1.232 लीटर है।

(ii) यहाँ, ऊँचाई (h) = 12 सेमी और तिर्यक ऊँचाई (l) = 13 सेमी

∴ शंक्वाकार बर्तन की धारिता

इस प्रकार, शंक्वाकार बर्तन की आवश्यक धारिता है1135लीटर.

प्रश्न 3.
एक शंकु की ऊँचाई 15 सेमी है। यदि इसका आयतन 1570 सेमी³ है, तो आधार की त्रिज्या ज्ञात कीजिए। (π = 3.14 का प्रयोग कीजिए)
हल:
यहाँ, शंकु की ऊँचाई (h) = 15 सेमी
शंकु का आयतन = 1570 सेमी³ मान
लीजिए आधार की त्रिज्या 'r' सेमी है।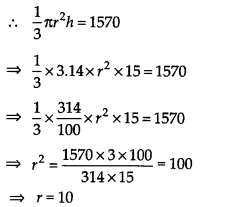

अत: आधार की अभीष्ट त्रिज्या 10 सेमी है।

प्रश्न 4.
यदि 9 सेमी ऊँचाई वाले एक लम्बवृत्तीय शंकु का आयतन 48 सेमी³ है, तो इसके आधार का व्यास ज्ञात कीजिए।
हल:
शंकु का आयतन = 48 सेमी³ शंकु
की ऊँचाई (h) = 9 सेमी
मान लीजिए r सेमी इसकी आधार त्रिज्या है।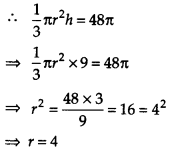

व्यास = 2 x त्रिज्या।
∴ शंकु के आधार का व्यास = (2 x 4) सेमी = 8 सेमी

प्रश्न 5.
3.5 मीटर ऊपरी व्यास वाला एक शंक्वाकार गड्ढा 12 मीटर गहरा है। इसकी धारिता किलोलीटर में क्या है?
हल:
यहाँ, शंक्वाकार गड्ढे का व्यास = 3.5 मीटर
त्रिज्या (r) =3.52m =3520m,
गहराई (h) = 12 मी
⇒ आयतन (धारिता) =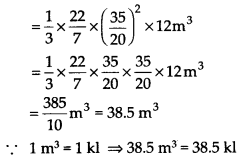13πr 2 h

इस प्रकार, शंक्वाकार गड्ढे की क्षमता 38.5 kl है।

प्रश्न 6.
एक लम्ब वृत्तीय शंकु का आयतन 9856 सेमी 3 है । यदि आधार का व्यास 28 सेमी है, तो ज्ञात कीजिए
(i) शंकु की ऊँचाई
(ii) शंकु की तिर्यक ऊँचाई
(iii) शंकु का वक्र पृष्ठीय क्षेत्रफल
हल:
शंकु का आयतन = 9856 सेमी 3
आधार का व्यास 28 सेमी
आधार की त्रिज्या (r) =282= 14 सेमी

(i) मान लीजिए शंकु की ऊँचाई h सेमी है।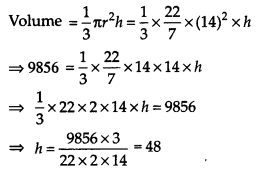

अतः अभीष्ट ऊँचाई 48 सेमी है।

(ii) माना तिर्यक ऊँचाई l सेमी है।
⇒ l 2 = r 2 + h 2
⇒ l 2 = 14 2 + 48 2 = 196 + 2304 = 2500
∴ l = 50
इस प्रकार, अभीष्ट तिर्यक ऊँचाई = 50 सेमी.

(iii) शंकु का वक्र पृष्ठीय क्षेत्रफल = πrl
∴ वक्र पृष्ठीय क्षेत्रफल =227x 14 x 50 सेमी 2
= 2200 सेमी 2
इस प्रकार, शंकु का वक्र पृष्ठीय क्षेत्रफल 2200 सेमी 2 है ।

प्रश्न 7.
5 सेमी, 12 सेमी और 13 सेमी भुजाओं वाला एक समकोण त्रिभुज ABC, 12 सेमी भुजा के परितः घुमाया जाता है। इस प्रकार प्राप्त ठोस का आयतन ज्ञात कीजिए।
हल:
समकोण त्रिभुज ABC की भुजाएँ 5 सेमी, 12 सेमी और 13 सेमी हैं।
समकोण त्रिभुज 12 सेमी भुजा के परितः घुमाया जाता है।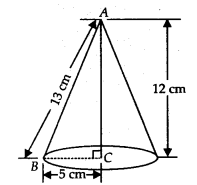

इस प्रकार, बने शंकु के आधार की त्रिज्या (r) = 5 सेमी
ऊँचाई (h) = 12 सेमी
∴ प्राप्त शंकु का आयतन =13πr 2 h
=13x π x (5) 2 x 12cm 3
= 100 π cm 3
इस प्रकार, शंकु का आवश्यक आयतन 100πcm 3 है ।

प्रश्न 8.
यदि उपरोक्त प्रश्न 7 में त्रिभुज ABC को 5 सेमी भुजा के चारों ओर घुमाया जाता है, तो प्राप्त ठोस का आयतन ज्ञात कीजिए। प्रश्न 7 और 8 में प्राप्त दोनों ठोसों के आयतनों का अनुपात भी ज्ञात कीजिए।
हल:
चूँकि समकोण त्रिभुज को 5 सेमी भुजा के चारों ओर घुमाया जाता है।
∴ प्राप्त शंकु की ऊँचाई (h) = 5 सेमी
शंकु की त्रिज्या (r) = 12 सेमी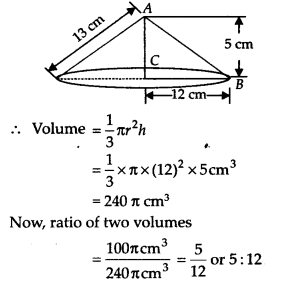

अतः, अभीष्ट अनुपात 5 : 12 है।

प्रश्न 9.
गेहूँ का एक ढेर शंकु के आकार का है जिसका व्यास 10.5 मीटर और ऊँचाई 3 मीटर है। इसका आयतन ज्ञात कीजिए। बारिश से बचाने के लिए ढेर को कैनवास से ढकना है। आवश्यक कैनवास का क्षेत्रफल ज्ञात कीजिए।
हल:
यहाँ, गेहूँ का ढेर एक शंकु के आकार का है जिसका आधार व्यास = 10.5 मीटर है।

अतः आवश्यक आयतन = 86.625 मीटर 3
अब, ढेर को ढकने के लिए कैनवास का क्षेत्रफल शंक्वाकार ढेर के वक्र पृष्ठीय क्षेत्रफल के बराबर होना चाहिए।

अतः कैनवास का आवश्यक क्षेत्रफल 99.825 मीटर 2 है ।

Ex 13.8

प्रश्न 1.
एक गोले का आयतन ज्ञात कीजिए जिसकी त्रिज्या
(i) 7 सेमी
(ii) 0.63 सेमी
हल:
(i) यहाँ, त्रिज्या (r) = 7 सेमी

इस प्रकार, अभीष्ट आयतन = 143713सेमी 3

(ii) यहाँ, त्रिज्या (r) = 0.63 मीटर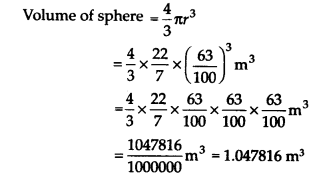

अतः, अभीष्ट आयतन 1.05 मीटर 3 (लगभग) है।

प्रश्न 2.
एक ठोस गोलाकार गेंद द्वारा विस्थापित पानी की मात्रा ज्ञात कीजिए जिसका व्यास
(i) 28 सेमी
(ii) 0.21 मीटर है
। हल:
(i) गेंद का व्यास = 28 सेमी
गेंद की त्रिज्या (r) सेमी282सेमी = 14 सेमी
गोलाकार गेंद का आयतन =43πr 3

(ii) गेंद का व्यास = 0.21 मीटर
⇒ त्रिज्या (r) =0.212मी =21200m

Thus, the amount of water displayed = 0.004851 m3.

प्रश्न 3.
एक धातु की गेंद का व्यास 4.2 सेमी है। यदि धातु का घनत्व 8.9 ग्राम प्रति सेमी 3 है, तो गेंद का द्रव्यमान क्या है ?
हल:
धातु की गेंद का व्यास = 4.2 सेमी
⇒ त्रिज्या (r) =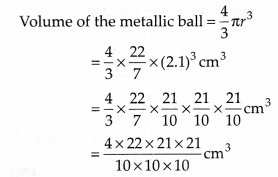4.22सेमी = 2.1 सेमी

धातु का घनत्व = 8.9 ग्राम प्रति सेमी 3

∴ गेंद का द्रव्यमान = 8.9 x [गेंद का आयतन]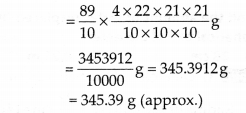

इस प्रकार, गेंद का द्रव्यमान 345.39 ग्राम (लगभग) है।

प्रश्न 4.
चंद्रमा का व्यास पृथ्वी के व्यास का लगभग एक-चौथाई है। चंद्रमा का आयतन पृथ्वी के आयतन का कितना भाग है?
हल:
मान लीजिए पृथ्वी का व्यास 2r है।
⇒ पृथ्वी की त्रिज्या =2r2= r
चूँकि, चंद्रमा का व्यास =14(पृथ्वी का व्यास)
⇒ चंद्रमा की त्रिज्या =14(पृथ्वी की त्रिज्या)
चन्द्रमा की त्रिज्या =14(r) =r4
∴ पृथ्वी का आयतन =43πr 3 और

प्रश्न 5.
10.5 सेमी व्यास वाले एक अर्धगोलाकार कटोरे में कितने लीटर दूध आ सकता है?
हल:
अर्धगोलाकार कटोरे का व्यास = 10.5 सेमी
⇒ अर्धगोलाकार कटोरे की त्रिज्या (r) =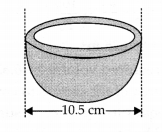10.52सेमी =10520सेमी

इस प्रकार, कटोरे की क्षमता = 0.303 लीटर (लगभग)

प्रश्न 6.
एक अर्धगोलाकार टैंक 1 सेमी मोटी लोहे की चादर से बना है। यदि आंतरिक त्रिज्या 1 मीटर है, तो टैंक बनाने में प्रयुक्त लोहे का आयतन ज्ञात कीजिए।
हल:
आंतरिक त्रिज्या (r) = 1 मीटर
∵ मोटाई = 1 सेमी =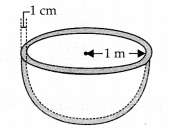1100m = 0.01m

∴ बाहरी त्रिज्या (R) = 1 m + 0.01 m = 1.01 m

इस प्रकार, प्रयुक्त लोहे का आवश्यक आयतन
= 0.06348 m 3 (लगभग)

प्रश्न 7.
एक गोले का आयतन ज्ञात कीजिए जिसका पृष्ठीय क्षेत्रफल 154 सेमी 2 है ।
हल:
माना गोले की त्रिज्या 'r' है।
∴इसका पृष्ठीय क्षेत्रफल = 4πr 2
4πr 2 = 154 [दिया है]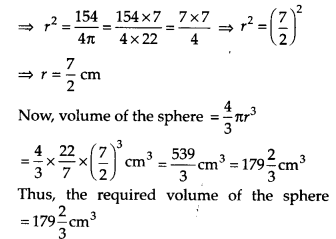

प्रश्न 8.
एक इमारत का गुंबद अर्धगोले के आकार का है। अंदर से इसकी सफेदी पुताई ₹498.96 की लागत से की गई। यदि सफेदी पुताई की लागत ₹2.00 प्रति वर्ग मीटर है, तो
(i) गुंबद का आंतरिक पृष्ठीय क्षेत्रफल,
(ii) गुंबद के अंदर हवा का आयतन ज्ञात कीजिए।
हल:
सफेदी पुताई की लागत = ₹498.96
प्रति वर्ग मीटर सफेदी पुताई की लागत = ₹2.00

प्रश्न 9.
सत्ताईस ठोस लोहे के गोले, जिनमें से प्रत्येक की त्रिज्या r और पृष्ठीय क्षेत्रफल S है, को पिघलाकर S' पृष्ठीय क्षेत्रफल वाला एक गोला बनाया गया है।
(i) नए गोले की त्रिज्या r',
(ii) S और S' का अनुपात ज्ञात कीजिए।
हल:
(i) मान लीजिए एक छोटे गोले की त्रिज्या r है
∴ इसका आयतन =43πr 3
27 छोटे गोलों का आयतन 27 x [43πr 3 ]
माना नए गोले की त्रिज्या r' है
∴ नए गोले का आयतन =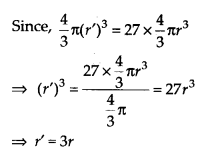43π(r') 3

अतः, नये गोले की त्रिज्या 3r है।

(ii) गोले का पृष्ठीय क्षेत्रफल = 4πr 2
= S = 4πr 2 और S' = 4π (3r) 2 [∵ r' = 3r]

इस प्रकार, S : S' = 1 : 9

Ex 13.9

प्रश्न 1.
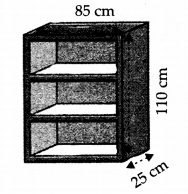
एक लकड़ी के बुकशेल्फ़ की बाहरी विमाएँ इस प्रकार हैं:
ऊँचाई = 110 सेमी, गहराई = 25 सेमी, चौड़ाई = 85 सेमी (चित्र देखें)। तख्ते की मोटाई हर जगह 5 सेमी है। बाहरी सतहों को पॉलिश करना है और भीतरी सतहों को रंगना है। यदि पॉलिश करने की दर 20 पैसे प्रति वर्ग सेमी है और पॉइंटिंग की दर 10 पैसे प्रति वर्ग सेमी है , तो बुकशेल्फ़ की सतह को पॉलिश करने और रंगने के लिए आवश्यक कुल व्यय ज्ञात कीजिए।

हल:
यहां, लंबाई (l) = 85 सेमी,
चौड़ाई (b) = 25 सेमी और ऊंचाई (h) = 110 सेमी
बाहरी सतह क्षेत्र = चार चेहरों का क्षेत्रफल + पीछे का क्षेत्रफल + सामने की बीडिंग का क्षेत्रफल
= [2 (110 + 85) x 25 + 110 x 85 + (110 x 5 x 2) + (75 x 5) x 4] सेमी 2 = 21700 सेमी 2
∴ बाहरी चेहरों को चमकाने की लागत = रु. (21700 x20100) = 4340 रुपये
आंतरिक सतह क्षेत्र = 75 सेमी x 30 सेमी x 20 सेमी आयाम वाले 3 घनाभों के पांच चेहरों का क्षेत्रफल
= 75 सेमी x 30 सेमी x 20 सेमी आयाम वाले 3 घनाभों का कुल सतह क्षेत्र - 75 सेमी x 30 सेमी x 20 सेमी आयाम वाले 3 घनाभों के आधारों का क्षेत्रफल 3(2(75 x 30 + 30 x 20 + 75 x 20)) सेमी 2 - 3 x (75 x 30) सेमी 2
= 6(2250 + 600 + 1500) सेमी 2 - 6750 सेमी 2 = 19350 सेमी 2
∴ आंतरिक चेहरों को पेंट करने की लागत = 19350 रुपये x10100= 1935 रुपये
इसलिए, कुल व्यय = (4340 + 1935)
रुपये = 6275 रुपये

प्रश्न 2.
एक घर की सामने की दीवार को 21 सेमी व्यास वाले लकड़ी के गोलों से सजाया गया है, जिन्हें आकृति में दिखाए अनुसार छोटे आधारों पर रखा गया है। इस उद्देश्य के लिए आठ ऐसे गोले उपयोग में लाए जाते हैं, और उन्हें चांदी के रंग से रंगा जाना है। प्रत्येक आधार 1.5 सेमी त्रिज्या और 7 सेमी ऊँचाई वाला एक बेलन है और इसे काले रंग से रंगा जाना है। यदि चांदी के रंग की लागत 25 पैसे प्रति वर्ग सेमी है और काले रंग की लागत 5 पैसे प्रति वर्ग सेमी है, तो रंगाई की लागत ज्ञात कीजिए। 

हल : 

यह

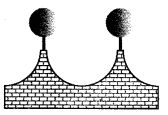
स्पष्ट
है कि चांदी के रंग की लागत की गणना करते समय हमें आधारों पर रखे गोले की लागत घटानी होगी।
चांदी के रंग से रंगा जाने वाला पृष्ठीय क्षेत्रफल

प्रश्न 3.
एक गोले का व्यास 25% कम कर दिया जाता है। इसका वक्र पृष्ठीय क्षेत्रफल कितने प्रतिशत कम हो जाता है?
हल:
मान लीजिए गोले का व्यास d है।
घटने के बाद, गोले का व्यास
= d –25100xd
= d –14d =34d
चूंकि, एक गोले का सतह क्षेत्र = 4πr 2 या π(2r) 2 या πd 2
एक गोले का सतह क्षेत्र, जब गोले का व्यास है

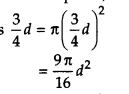
अब, घुमावदार सतह क्षेत्र में प्रतिशत कमी