NCERT Class 9 Maths Chapter 12 हीरोन सूत्र

 NCERT Class 9 Maths Chapter 12 हीरोन सूत्र

NCERT Solutions for Class 9 Maths Chapter 12 हीरोन सूत्र

Ex 12.1

प्रश्न 1.
एक ट्रैफ़िक सिग्नल बोर्ड, जिस पर 'आगे स्कूल है' लिखा है, एक समबाहु त्रिभुज है जिसकी भुजा a है। हीरोन के सूत्र का उपयोग करके सिग्नल बोर्ड का क्षेत्रफल ज्ञात कीजिए। यदि इसका परिमाप 180 सेमी है, तो सिग्नल बोर्ड का क्षेत्रफल क्या होगा?
हल:
मान लीजिए समबाहु त्रिभुज की प्रत्येक भुजा a है।
त्रिभुज का अर्ध-परिमाप,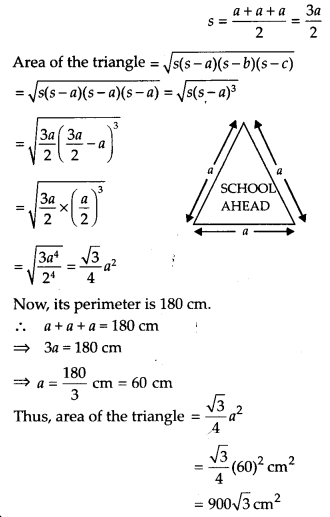

प्रश्न 2.
एक फ्लाईओवर की त्रिकोणीय दीवारों का उपयोग विज्ञापनों के लिए किया गया है। दीवारों की भुजाएँ 122 मीटर, 22 मीटर और 120 मीटर हैं (चित्र देखें)। विज्ञापनों से प्रति वर्ष प्रति वर्ग मीटर ₹5000 की आय होती है। एक कंपनी ने इसकी एक दीवार 3 महीने के लिए किराए पर ली। उसने कितना किराया दिया?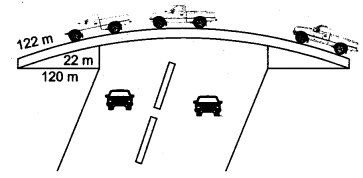

हल:
मान a = 122 मीटर,
b = 22 मीटर
c = 120 मीटर
हमें मिलता है, b 2 + c 2 = (22) 2 + (120) 2 = 484 + 14400 = 14884 = (122) 2 = a 2
अतः, पार्श्व दीवारें समकोण त्रिभुज के आकार में हैं।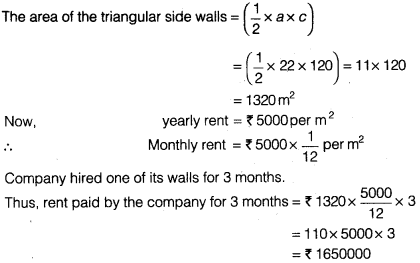

प्रश्न 3.
एक पार्क में एक स्लाइड है। इसकी एक दीवार को कंपनी ने 3 महीने के लिए किराए पर लिया है। दीवारों को किसी रंग से रंगा गया है और उस पर "पार्क को हरा-भरा और स्वच्छ रखें" संदेश लिखा है (चित्र देखें)। यदि दीवार की भुजाएँ 15 मीटर, 11 मीटर और 6 मीटर हैं, तो रंग से रंगे गए क्षेत्र का क्षेत्रफल ज्ञात कीजिए।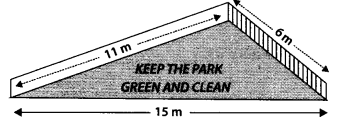

हल:
मान लीजिए दीवार की भुजाएँ
a = 15 मीटर, b = 11 मीटर, c = 6 मीटर
अर्ध-परिमाप हैं।

इस प्रकार, रंग से रंगा गया आवश्यक क्षेत्र
= 20√2 मीटर 2

प्रश्न 4.
एक त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसकी दो भुजाएँ 18 सेमी और 10 सेमी हैं और परिमाप 42 सेमी है।
हल:
माना त्रिभुज की भुजाएँ a = 18 सेमी, b = 10 सेमी और c = x सेमी हैं
क्योंकि, त्रिभुज का परिमाप = 42 सेमी
∴ 18 सेमी + 10 सेमी + x सेमी = 42
x = [42 – (18 + 10) सेमी = 14 सेमी
अब, अर्ध-परमाणु, s =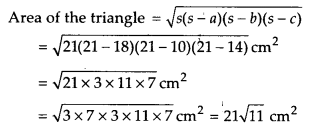422सेमी = 21 सेमी

अतः त्रिभुज का अभीष्ट क्षेत्रफल = 2111−−√सेमी 2

प्रश्न 5.
एक त्रिभुज की भुजाएँ 12 : 17 : 25 के अनुपात में हैं और इसका परिमाप 540 सेमी है। इसका क्षेत्रफल ज्ञात कीजिए।
हल:
माना त्रिभुज की भुजाएँ
a = 12x सेमी, b = 17x सेमी, c = 25x सेमी
त्रिभुज का परिमाप = 540 सेमी
अब, 12x + 17x + 25x = 540
⇒ 54x = 54 ⇒ x = 10
∴ a = (12 x 10) सेमी = 120 सेमी,
b = (17 x 10) सेमी = 170 सेमी
और c = (25 x 10) सेमी = 250 सेमी
अब, अर्ध-परिमाप, s =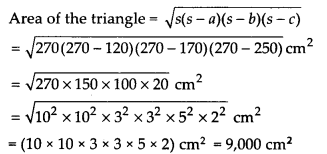5402सेमी = 270 सेमी

प्रश्न 6.
एक समद्विबाहु त्रिभुज का परिमाप 30 सेमी है और प्रत्येक बराबर भुजा 12 सेमी है। त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
हल:
मान लीजिए कि एक समद्विबाहु त्रिभुज की भुजाएँ
a = 12 सेमी, b = 12 सेमी, c = x सेमी हैं।
चूँकि, त्रिभुज का परिमाप = 30 सेमी
∴ 12 सेमी + 12 सेमी + x सेमी = 30 सेमी
⇒ x = (30 – 24) = 6
अब, अर्ध-परिमाप, s =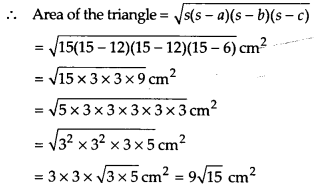302सेमी =15 सेमी

इस प्रकार, त्रिभुज का अभीष्ट क्षेत्रफल = 9√15 सेमी 2

Ex 12.2

प्रश्न 1.
एक पार्क चतुर्भुज ABCD के आकार का है, जिसमें ∠C = 90°, AB = 9 मीटर, BC = 12 मीटर, CD = 5 मीटर और AD = 8 मीटर है।
इसका क्षेत्रफल कितना है?
हल:
दिया गया है: एक चतुर्भुज ABCD जिसमें ZC = 90°, AB = 9 मीटर, BC = 12 मीटर, CD = 5 मीटर और AD = 8 मीटर है।
आइए B और D को इस प्रकार मिलाएँ कि ABCD एक समकोण त्रिभुज बन जाए।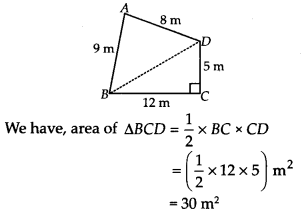

अब, ∆ABD का क्षेत्रफल ज्ञात करने के लिए, हमें BD की लंबाई चाहिए।
समकोण ∆BCD में, पाइथागोरस प्रमेय द्वारा
BD 2 = 50 2 + CD 2
⇒ BD 2 = 12 2 + 5 2
⇒ BD 2 = 144 + 25 = 169
⇒ BD = 13 मीटर
अब, ∆ABD के लिए, हमारे पास है
a = AB = 9 मीटर, b = AD = 8 मीटर, c = BD = 13 मीटर

∴ चतुर्भुज ABCD का क्षेत्रफल = ∆BCD का क्षेत्रफल + ∆ABD का क्षेत्रफल = 30 मीटर 2 + 35.5 मीटर 2
= 65.5 मीटर 2 (लगभग)

प्रश्न 2.
चतुर्भुज ABCD का क्षेत्रफल ज्ञात कीजिए जिसमें AB = 3 सेमी, BC = 4 सेमी, CD = 4 सेमी, DA = 5 सेमी और AC = 5 सेमी है।
हल:
एक चतुर्भुज ABCD दिया गया है जिसमें AB = 3 सेमी, BC = 4 सेमी, CD = 4 सेमी, DA = 5 सेमी और AC = 5 सेमी है।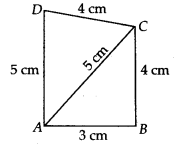

∆ABC के लिए, a = AB = 3 सेमी, b = BC = 4 सेमी और c = AC = 5 सेमी

अब, चतुर्भुज ABCD का क्षेत्रफल = ∆ABC का क्षेत्रफल + ∆ACD का क्षेत्रफल
= 6 सेमी 2 + 9.2 सेमी 2 = 15.2 सेमी 2 (लगभग)

प्रश्न 3.
राधा ने रंगीन कागज़ से एक हवाई जहाज़ का चित्र बनाया जैसा कि चित्र में दिखाया गया है। प्रयुक्त कागज़ का कुल क्षेत्रफल ज्ञात कीजिए।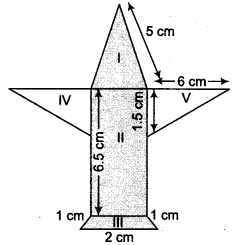

हल:
पृष्ठ I के लिए:
यह एक समद्विबाहु त्रिभुज है जिसकी भुजाएँ a = 5 सेमी, b = 5 सेमी, c = 1 सेमी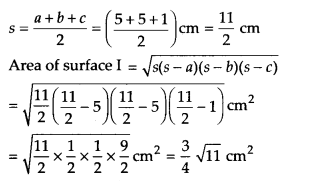

= (0.75 x 3.3) सेमी 2
= 2.475 सेमी 2 (लगभग)

सतह II के लिए:
यह एक आयत है जिसकी लंबाई 6.5 सेमी और चौड़ाई 1 सेमी है।
∴ सतह II का क्षेत्रफल = लंबाई x चौड़ाई
= (6.5 x 1) सेमी 2 = 6.5 सेमी 2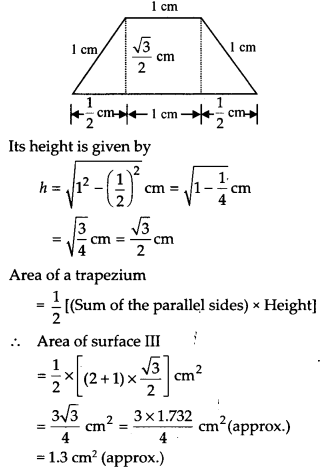

सतह III के लिए:
यह एक समलम्ब चतुर्भुज है जिसकी समान्तर भुजाएँ 1 सेमी और 2 सेमी हैं जैसा कि नीचे दी गई आकृति में दिखाया गया है: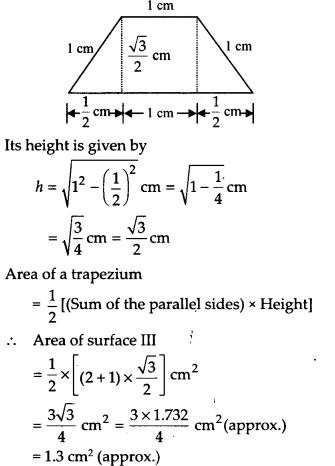

सतह IV और V के लिए:
सतह V एक समकोण त्रिभुज है जिसका आधार 6 सेमी और ऊँचाई 1.5 सेमी है।
साथ ही, सतह IV का क्षेत्रफल = सतह V का क्षेत्रफल
=12x आधार x ऊँचाई
= (12x 6 x 15) सेमी 2 = 4.5 सेमी 2
इस प्रकार, उपयोग किए गए कागज का कुल क्षेत्रफल = (सतह I का क्षेत्रफल) + (सतह II का क्षेत्रफल) + (सतह III का क्षेत्रफल) + (सतह IV का क्षेत्रफल) + (सतह V का क्षेत्रफल) = [2.475 + 6.5 + 1.3 + 4.5 + 4.5] सेमी 2
= 19.275 सेमी 2
= 19.3 सेमी 2 (लगभग)

प्रश्न 4.
एक त्रिभुज और एक समांतर चतुर्भुज का आधार और क्षेत्रफल समान है। यदि त्रिभुज की भुजाएँ 26 सेमी, 28 सेमी और 30 सेमी हैं, और समांतर चतुर्भुज 28 सेमी के आधार पर स्थित है, तो समांतर चतुर्भुज की ऊँचाई ज्ञात कीजिए।
हल:
दिए गए त्रिभुज के लिए, हमारे पास है a = 28 सेमी, b = 30 सेमी, c = 26 सेमी।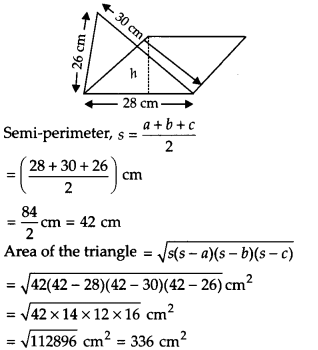

दिए गए समांतर चतुर्भुज का क्षेत्रफल = दिए गए त्रिभुज का क्षेत्रफल
∴ समांतर चतुर्भुज का क्षेत्रफल = 336 सेमी 2
⇒ आधार x ऊँचाई = 336
⇒ 28 x h = 336, जहाँ 'h' समांतर चतुर्भुज की ऊँचाई है।
⇒ h =33628= 12
अतः समांतर चतुर्भुज की अभीष्ट ऊँचाई = 12 सेमी

प्रश्न 5.
एक समचतुर्भुजाकार खेत में 18 गायों के चरने के लिए हरी घास है। यदि समचतुर्भुज की प्रत्येक भुजा 30 मीटर है और इसका लंबा विकर्ण 48 मीटर है, तो प्रत्येक गाय को घास के मैदान का कितना क्षेत्रफल मिलेगा?
हल:
यहाँ, समचतुर्भुज की प्रत्येक भुजा = 30 मीटर।
मान लीजिए ABCD दिया गया समचतुर्भुज है और विकर्ण BD = 48 मीटर है।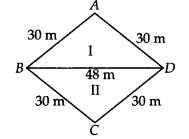

∆ABC की भुजाएँ हैं: a = AB = 30 मीटर, b = AD = 30 मीटर, c = BD = 48 मीटर।

चूँकि, एक विकर्ण समचतुर्भुज को दो सर्वांगसम त्रिभुजों में विभाजित करता है।
∴ त्रिभुज II का क्षेत्रफल = 432 मी 2
अब, समचतुर्भुज का कुल क्षेत्रफल = त्रिभुज I का क्षेत्रफल + त्रिभुज II का क्षेत्रफल
= 432 मी 2 + 432 मी 2 = 864 मी 2
18 गायों के चरने के लिए घास का क्षेत्रफल = 864 मी 2
⇒ 1 गाय के चरने के लिए घास का क्षेत्रफल =86418मी 2
= 48 मी 2

प्रश्न 6.
दो अलग-अलग रंगों के कपड़े के 10 त्रिकोणीय टुकड़ों को सिलकर एक छाता बनाया गया है (चित्र देखें), प्रत्येक टुकड़े की माप 20 सेमी, 50 सेमी और 50 सेमी है। छाते के लिए प्रत्येक रंग का कितना कपड़ा चाहिए?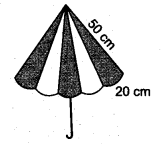

हल:
मान लीजिए प्रत्येक त्रिकोणीय टुकड़े की भुजाएँ
a = 20 सेमी, b = 50 सेमी, c = 50 सेमी हैं।

प्रश्न 7.
32 सेमी विकर्ण वाले एक वर्ग और 8 सेमी आधार और 6 सेमी भुजाओं वाले एक समद्विबाहु त्रिभुज के आकार की एक पतंग, आकृति में दिखाए अनुसार तीन अलग-अलग रंगों से बनाई जानी है। इसमें प्रत्येक रंग का कितना कागज इस्तेमाल किया गया है?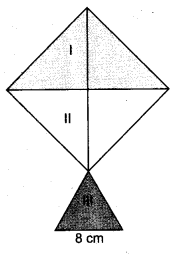

हल:
कागज के प्रत्येक रंग को 3 त्रिभुजों अर्थात् I, II, III में विभाजित किया गया है।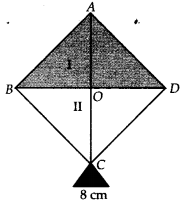

8 सेमी
त्रिभुज I के लिए:
ABCD एक वर्ग है [दिया है]
∵ एक वर्ग के विकर्ण बराबर होते हैं और एक दूसरे को समद्विभाजित करते हैं।
∴ AC = BD = 32 सेमी
AABD की ऊँचाई = OA = (12
= 16 सेमी
त्रिभुज I का क्षेत्रफल = (122
= 256 सेमी 2

त्रिभुज II के लिए:
चूँकि, एक वर्ग का विकर्ण उसे दो सर्वांगसम त्रिभुजों में विभाजित करता है।
इसलिए, त्रिभुज II का क्षेत्रफल = त्रिभुज I का क्षेत्रफल
∴ त्रिभुज II का क्षेत्रफल = 256 सेमी 2

त्रिभुज III के लिए:
भुजाएँ a = 8 सेमी, b = 6 सेमी और c = 6 सेमी दी गई हैं।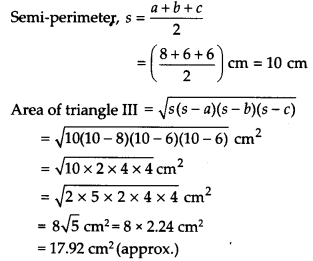

इस प्रकार, विभिन्न रंगों का क्षेत्रफल है:
छाया I का क्षेत्रफल = 256 सेमी 2
छाया II का क्षेत्रफल = 256 सेमी 2
और छाया III का क्षेत्रफल = 17.92 सेमी 2

प्रश्न 8.
फर्श पर एक पुष्प डिज़ाइन 16 त्रिभुजाकार टाइलों से बना है, त्रिभुज की भुजाएँ 9 सेमी, 28 सेमी और 35 सेमी हैं (आकृति देखें)। 50 पैसे प्रति सेमी की दर से टाइलों को पॉलिश करने की लागत ज्ञात कीजिए।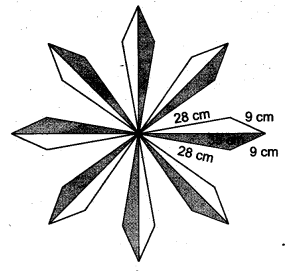

हल:
माना त्रिभुज की भुजाएँ a = 9 सेमी, b = 28 सेमी, c = 35 सेमी

सभी 16 त्रिभुजों का कुल क्षेत्रफल = (16 x 88.2) सेमी 2 = 1411.2 सेमी 2 (लगभग)
टाइलों को पॉलिश करने की लागत = रु. 0.5 प्रति सेमी 2
∴ सभी टाइलों को पॉलिश करने की लागत = रु. (0.5 x 1411.2) = रु. 705.60 (लगभग)

प्रश्न 9.
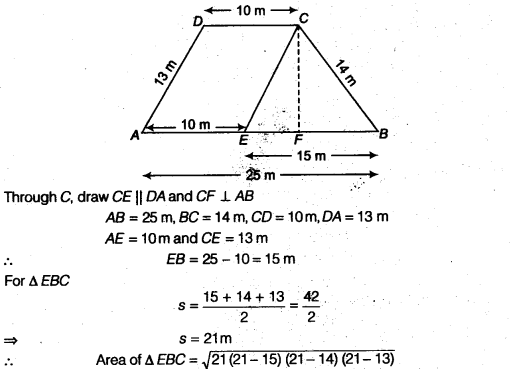
एक खेत समलम्ब चतुर्भुज के आकार का है जिसकी समांतर भुजाएँ 25 मीटर और 10 मीटर हैं। असमांतर भुजाएँ 14 मीटर और 13 मीटर हैं। खेत का क्षेत्रफल ज्ञात कीजिए।
हल:
यहाँ, ABCD एक समलम्ब चतुर्भुज है और AB || DC है।