NCERT Class 9 Maths Chapter 11 रचनाएँ

 NCERT Class 9 Maths Chapter 11 रचनाएँ

NCERT Solutions for Class 9 Maths Chapter 11 रचनाएँ

Ex 11.1

प्रश्न 1.
किसी दी गई किरण के प्रारंभिक बिंदु पर 90° का कोण बनाइए और निर्माण का औचित्य सिद्ध कीजिए।
हल:
निर्माण के चरण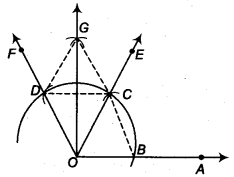

1. O को केन्द्र मानकर तथा कुछ त्रिज्या लेकर एक वृत्त का चाप खींचिए जो OA को बिन्दु B पर प्रतिच्छेद करता है।
2. B को केन्द्र मानकर तथा पहले वाली त्रिज्या लेकर एक चाप खींचिए जो पहले खींचे गए चाप को बिन्दु C पर प्रतिच्छेदित करता है।
3. C को केन्द्र मानकर तथा पहले की तरह समान त्रिज्या लेकर एक चाप खींचिए जो चरण 1 में खींचे गए चाप को D पर प्रतिच्छेदित करता है।
4. C से गुजरने वाली किरण OE खींचिए।
   तब, ∠EOA = 60°
5. D से गुजरने वाली किरण खींचें। फिर, ∠FOE = 60°।
6. इसके बाद, C और D को केंद्र मानकर और 12 CD से अधिक त्रिज्या लेकर, एक दूसरे को G पर प्रतिच्छेद करने के लिए चाप खींचिए।
7. किरण OG खींचिए। यह किरण OG, ∠FOE का समद्विभाजक है, अर्थात,
   ∠FOG = ∠EOG = 12 ∠FOE = 12 (60°) = 30°
   इस प्रकार, ∠GOA = ∠GOE + ∠EOA
   = 30° + 60° = 90°

औचित्य
(i) BC को मिलाइए।
तब, OC=OB = BC (रचना से)
∴ ∆COB एक समबाहु त्रिभुज है।
∴ ∠COB = 60°
∴ ∠EOA = 60°

(ii) CD को मिलाइए।
तब, OD=OC=CD (रचना से)
∴ ∆DOC एक समबाहु त्रिभुज है।
∴ ∠DOC = 60°
∴ ∠FOE = 60°

(iii) CG और DG को मिलाएँ।
∆ODG और ∆OCG में,
OD = OC (एक ही चाप की त्रिज्याएँ)
DG = CG (बराबर त्रिज्याओं के चाप)
OG = OG (उभयनिष्ठ)
∴ ∆ ODG ≅ ∆OCG (SSS नियम)
∴ ∠DOG = ∠COG (CPCT)
∴ ∠FOG = ∠EOG = 12 ∠FOE
= 12 (60°) = 30°
इस प्रकार, ∠GOA = ∠GOE + ∠EOA = 30° + 60° = 90°

प्रश्न 2.
किसी दी गई किरण के प्रारंभिक बिंदु पर 45° का कोण बनाइए और इस रचना का औचित्य सिद्ध कीजिए।
हल:
रचना के चरण

1. O को केन्द्र मानकर तथा कुछ त्रिज्या लेकर एक वृत्त का चाप खींचिए जो OA को बिन्दु B पर प्रतिच्छेद करता है।
2. B को केन्द्र मानकर तथा पहले वाली त्रिज्या लेकर एक चाप खींचिए जो पहले खींचे गए चाप को बिन्दु C पर प्रतिच्छेदित करता है।
   
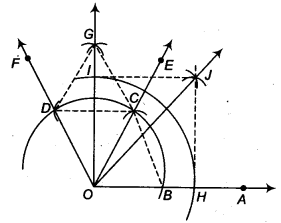
3. C को केन्द्र मानकर तथा पहले की तरह समान त्रिज्या लेकर एक चाप खींचिए जो चरण 1 में खींचे गए चाप को D पर प्रतिच्छेदित करता है।
4. C से गुजरने वाली किरण OE खींचिए। तब, ∠EOA = 60° होगा।
5. D से गुजरने वाली किरण OF खींचिए। तब, ∠FOE = 60°।
6. इसके बाद, C और D को केंद्र मानकर और \(\frac { 1 }{ 2 }\) CD से अधिक त्रिज्या लेकर, एक दूसरे को G पर प्रतिच्छेद करने के लिए चाप खींचिए।12CD पर एक दूसरे को प्रतिच्छेद करने के लिए चाप खींचिए, मान लीजिए G पर।
7. किरण OG खींचिए। यह किरण OG, ∠FOE का समद्विभाजक है,
   अर्थात, ∠FOG = ∠EOG = \(\frac { 1 }{ 2 }\) ∠FOE = \(\frac { 1 }{ 2 }\) (60°) = 30°.12∠FOE =12(60°) = 30°.
   इस प्रकार, ∠GOA = ∠GOE + ∠EOA
   = 30° + 60° = 90°
8. अब O को केन्द्र मानकर तथा कोई त्रिज्या लेकर, किरणों OA तथा OG को क्रमशः भुजा / पर प्रतिच्छेद करने के लिए एक चाप खींचिए।
9. इसके बाद, H और लास केंद्र लेते हुए और त्रिज्या \(\frac { 1 }{ 2 }\) Hl से अधिक लेकर, रेखा खींचें12Hl,
   एक दूसरे को J पर प्रतिच्छेद करने के लिए चाप खींचें।
10. किरण OJ खींचिए। यह किरण OJ, ∠GOA का अभीष्ट समद्विभाजक है।
    ∠GOJ = ∠AOJ = \(\frac { 1 }{ 2 }\) ∠GOA12∠GOA
    = \(\frac { 1 }{ 2 }\) (90°) = 45°12(90°) = 45°

औचित्य
(i) BC को मिलाइए। (रचना से)
तब, OC = OB = BC
∴ ∆COB एक समबाहु त्रिभुज है।
∴ ∠COB = 60°
∴ ∠EOA = 60°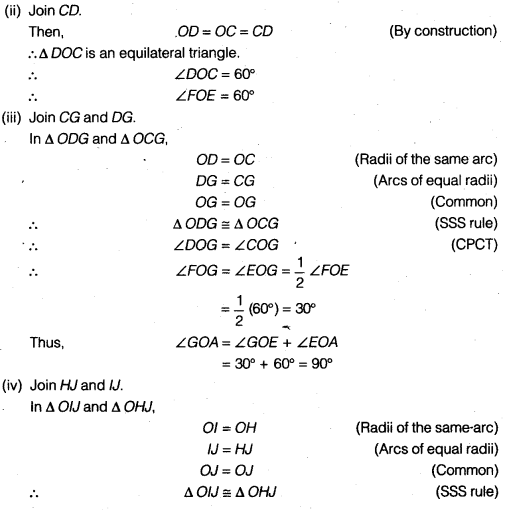

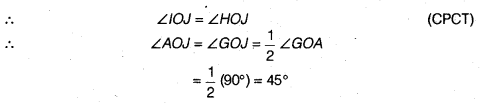
प्रश्न 3.
निम्नलिखित मापों के कोणों की रचना कीजिए
(i) 30°
(ii) 2212∘
(iii) 15°
हल:
(i) निर्माण के चरण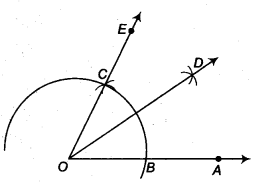

1. O को केन्द्र मानकर तथा कुछ त्रिज्या लेकर एक वृत्त का चाप खींचिए जो OA को बिन्दु B पर प्रतिच्छेद करता है।
2. B को केन्द्र मानकर तथा पहले वाली त्रिज्या लेकर एक चाप खींचिए जो पहले खींचे गए चाप को बिन्दु C पर प्रतिच्छेदित करता है।
3. C से गुजरने वाली किरण OE खींचिए। तब, ∠EOA = 60° होगा।
4. B और C को केंद्र मानकर और \(\frac { 1 }{ 2 }\) BC से अधिक त्रिज्या लेकर, एक दूसरे को D पर प्रतिच्छेद करने के लिए चाप खींचिए।12BC पर एक दूसरे को प्रतिच्छेद करने के लिए चाप खींचिए, मान लीजिए D पर।
5. किरण OD खींचिए, यह किरण OD, ∠EOA की समद्विभाजक है, अर्थात,
   ∠EOD = ∠AOD = \(\frac { 1 }{ 2 }\) ∠EOA = \(\frac { 1 }{ 2 }\) (60°) = 30°12∠ईओए =12(60°) = 30°

(ii) निर्माण के चरण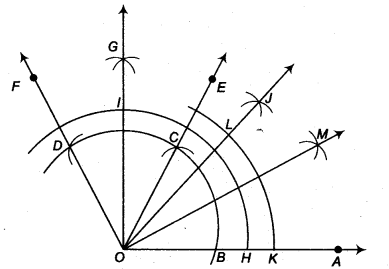

1. O को केन्द्र मानकर तथा कुछ त्रिज्या लेकर एक वृत्त का चाप खींचिए जो OA को बिन्दु B पर प्रतिच्छेद करता है।
2. B को केन्द्र मानकर तथा पहले वाली त्रिज्या लेकर एक चाप खींचिए जो पहले खींचे गए चाप को बिन्दु C पर प्रतिच्छेदित करता है।
3. C को केन्द्र मानकर तथा पहले की तरह समान त्रिज्या लेकर, चरण 1 में खींचे गए चाप को D पर प्रतिच्छेदित करने वाला चाप खींचा।
4. C से गुजरने वाली किरण OE खींचिए। तब, ∠EOA = 60° होगा।
5. D से गुजरने वाली किरण OF खींचिए। तब, ∠FOE = 60°।
6. इसके बाद, C और D को केंद्र मानकर और \(\frac { 1 }{ 2 }\)CD से अधिक त्रिज्या लेकर, एक दूसरे को G पर प्रतिच्छेद करने के लिए चाप खींचिए।12CD पर एक दूसरे को प्रतिच्छेद करने के लिए चाप खींचिए, मान लीजिए G पर।
7. किरण OG खींचिए। यह किरण OG, ∠FOE का समद्विभाजक है,
   
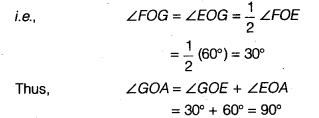
8. अब O को केन्द्र मानकर तथा कोई त्रिज्या लेकर, किरणों OA तथा OG को क्रमशः H तथा l पर प्रतिच्छेद करने के लिए एक चाप खींचिए।
9. इसके बाद, H और l को केंद्र मानकर और \(\frac { 1 }{ 2 }\)Hl से अधिक त्रिज्या लेकर, एक दूसरे को J पर प्रतिच्छेद करने के लिए चाप खींचिए।12Hl, एक दूसरे को J पर प्रतिच्छेद करने के लिए चाप खींचें।
10. किरण OJ खींचिए। यह किरण OJ, ∠GOA का समद्विभाजक है
    , अर्थात् ∠GOJ = ∠AOJ =12∠GOA
    =12(90°) = 45°
11. अब O को केन्द्र मानकर तथा कोई त्रिज्या लेकर, किरणों OA तथा OJ को क्रमशः K तथा L पर प्रतिच्छेद करने के लिए एक चाप खींचा।
12. इसके बाद, K और L को केंद्र मानकर त्रिज्या को √3 से अधिक रखें।12केएल, एक दूसरे को प्रतिच्छेद करने के लिए चाप खींचें, मान लीजिए H पर।
13. किरण OM खींचिए। यह किरण OM, ∠AOJ का समद्विभाजक है, अर्थात् ∠JOM = ∠AOM
    =12∠AOJ =12(45°) = 2212°

(iii) निर्माण के चरण

1. O को केन्द्र मानकर तथा कुछ त्रिज्या लेकर एक वृत्त का चाप खींचिए जो OA को बिन्दु B पर प्रतिच्छेद करता है।
2. B को केंद्र मानकर तथा पहले की तरह समान त्रिज्या लेकर एक चाप खींचिए जो पहले खींचे गए चाप को बिंदु C पर प्रतिच्छेदित करता है।
3. C से गुजरने वाली किरण OE खींचिए। तब, ∠EOA = 60° होगा।
   
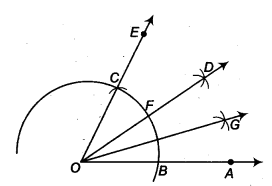
4. अब, 6 और Cas केंद्र लेते हुए और त्रिज्या से अधिक के साथ12BC पर एक दूसरे को प्रतिच्छेद करने के लिए चाप खींचिए, मान लीजिए D पर।
5. चरण 1 में खींचे गए चाप को F पर प्रतिच्छेद करती हुई किरण OD खींचिए। यह किरण OD, ∠EOA का समद्विभाजक है, अर्थात,
   ∠EOD = ∠AOD =12∠ईओए =12(60°) = 30°
6. अब, B और F को केंद्र मानकर तथा त्रिज्या को ∠ से अधिक लेकर12BF, एक दूसरे को प्रतिच्छेदित करने के लिए चाप खींचें, मान लीजिए G पर।
   1. किरण OG खींचिए। यह किरण OG, ∠AOD का समद्विभाजक है,
      अर्थात, ∠DOG = ∠AOG =12∠AOD =12(30°) = 15°

प्रश्न 4.
निम्नलिखित कोणों की रचना कीजिए और उन्हें चाँदे से मापकर सत्यापित कीजिए
(i) 75°
(ii) 105°
(iii) 135°
हल:
(i) रचना के चरण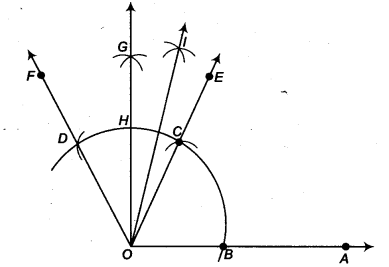

1. O को केन्द्र मानकर तथा कुछ त्रिज्या लेकर एक वृत्त का चाप खींचिए जो OA को बिन्दु B पर प्रतिच्छेद करता है।
2. B को केन्द्र मानकर तथा पहले वाली त्रिज्या लेकर एक चाप खींचिए जो पहले खींचे गए चाप को बिन्दु C पर प्रतिच्छेदित करता है।
3. C को केन्द्र मानकर तथा पहले की तरह समान त्रिज्या लेकर एक चाप खींचिए जो चरण 1 में खींचे गए चाप को D पर प्रतिच्छेदित करता है।
4. C से गुजरने वाली किरण OE को मिलाइए। तब, ∠EOA = 60°।
5. D से गुजरने वाली किरण खींचें। फिर, ∠FOE = 60°।
6. इसके बाद, C और D को केंद्र मानकर त्रिज्या को √3 से अधिक रखें।12CD पर एक दूसरे को प्रतिच्छेद करने के लिए चाप खींचिए, मान लीजिए G पर।
7. चरण 1 के चाप को H पर प्रतिच्छेद करती हुई किरण OG खींचिए। यह किरण OG, ∠FOE का समद्विभाजक है, अर्थात, ∠FOG = ∠EOG
   =12∠FOE =12(60°) = 30°
8. इसके बाद, C और H को केंद्र मानकर, त्रिज्या ± से अधिक लें।12CH,
   एक दूसरे को l पर प्रतिच्छेद करने वाले चाप खींचिए।
   किरण OI खींचिए। यह किरण OI, ∠GOE का समद्विभाजक है,
   अर्थात ∠GOI = ∠EOI =12∠GOE =12(30°) = 15°
   इस प्रकार, ∠IOA = ∠IOE + ∠EOA
   =15°+ 60° = 75°
   चाँदे द्वारा ∠IOA मापने पर, हम पाते हैं कि ∠IOA = 15°
   इस प्रकार, निर्माण सत्यापित है।

(ii) निर्माण के चरण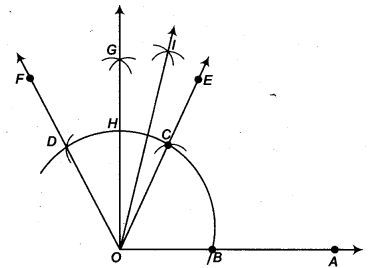

1. O को केन्द्र मानकर तथा कुछ त्रिज्या लेकर एक वृत्त का चाप खींचिए जो OA को बिन्दु B पर प्रतिच्छेद करता है।
2. B को केन्द्र मानकर तथा पहले वाली त्रिज्या लेकर एक चाप खींचिए जो पहले खींचे गए चाप को बिन्दु C पर प्रतिच्छेदित करता है।
3. C को केन्द्र मानकर तथा पहले की तरह समान त्रिज्या लेकर एक चाप खींचिए जो चरण 1 में खींचे गए चाप को बिन्दु D पर प्रतिच्छेदित करता है।
4. C से गुजरने वाली किरण Of खींचिए। तब, ∠EOA = 60° है।
5. D से गुजरने वाली किरण OF खींचिए। तब, ∠FOE = 60°।
6. इसके बाद, कैंड दास केंद्र लेते हुए और त्रिज्या से अधिक के साथ12CD पर एक दूसरे को प्रतिच्छेद करने के लिए चाप खींचिए, मान लीजिए G पर।
7. चरण 1 में खींचे गए चाप को H पर प्रतिच्छेद करती हुई किरण OG खींचिए। यह किरण OG, ∠FOE का समद्विभाजक है, अर्थात्,
   
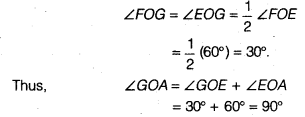
8. इसके बाद, H और D को केंद्र मानकर त्रिज्या को √3 से अधिक रखें।12HD पर, एक दूसरे को प्रतिच्छेद करने के लिए चाप खींचें, मान लीजिए l पर।
9. किरण Ol खींचिए। यह किरण Ol, ∠FOG का समद्विभाजक है, अर्थात्
   
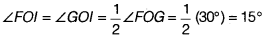
   , ∠lOA = ∠IOG + ∠GOA = 15° + 90° = 105°। चाँदे से ∠lOA मापने पर, हम पाते हैं कि ∠FOA = 105° है।
   इस प्रकार, रचना सत्यापित हो जाती है।
   
   

(iii) निर्माण के चरण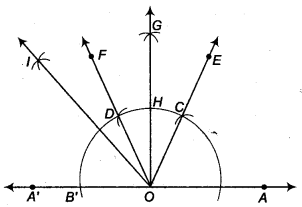

1. किरण OA' बनाने के लिए AO को A' तक बढ़ाएँ।
2. O को केन्द्र मानकर तथा कुछ त्रिज्या लेकर एक वृत्त का चाप खींचिए जो OA को बिन्दु B पर तथा OA' को बिन्दु B' पर प्रतिच्छेद करता है।
3. B को केंद्र मानकर और पहले की तरह समान त्रिज्या लेकर एक चाप खींचिए जो पहले खींचे गए चाप को बिंदु C पर काटता है।
4. C को केन्द्र मानकर तथा पहले की तरह समान त्रिज्या लेकर एक चाप खींचिए जो चरण 1 में खींचे गए चाप को D पर प्रतिच्छेदित करता है।
5. C से गुजरने वाली किरण OE खींचिए, तो ∠EOA = 60° होगा।
6. D से गुजरने वाली किरण OF खींचिए, तो ∠FOE = 60° होगा।
7. इसके बाद, C और D को केंद्र मानकर त्रिज्या को √3 से अधिक रखें।12CD पर एक दूसरे को प्रतिच्छेद करने के लिए चाप खींचिए, मान लीजिए G पर।
8. चरण 1 में खींचे गए चाप को H पर प्रतिच्छेद करने वाली किरण OG खींचिए। यह किरण OG, ∠FOE का समद्विभाजक है, अर्थात्,
   
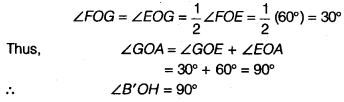
9. इसके बाद, B' और H को केंद्र मानकर, त्रिज्या को से अधिक लेकर12B'H, एक दूसरे को प्रतिच्छेद करने के लिए चाप खींचे गए, मान लीजिए l पर।
10. किरण Ol खींचिए। यह किरण Ol, ∠B'OG का समद्विभाजक है।
    
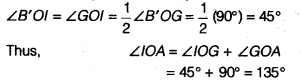
    चाँदे से ∠IOA मापने पर, हम पाते हैं कि ∠lOA = 135° है।
    इस प्रकार, रचना सत्यापित हो जाती है।

प्रश्न 5.
एक समबाहु त्रिभुज की रचना कीजिए, जिसकी भुजा दी गई हो और रचना का औचित्य दीजिए।
हल:
रचना के चरण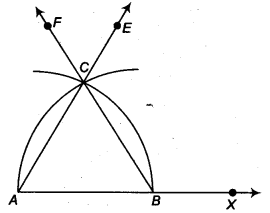

1. प्रारंभिक बिंदु A लेकर किरण AX लीजिए। AX से AB = 4 सेमी काट लीजिए।
2. A को केन्द्र मानकर तथा त्रिज्या (= 4 सेमी) लेकर एक वृत्त का चाप खींचिए जो AX को बिन्दु B पर प्रतिच्छेद करता है।
3. B को केन्द्र मानकर तथा पहले वाली त्रिज्या लेकर एक चाप खींचिए जो पहले खींचे गए चाप को बिन्दु C पर प्रतिच्छेदित करता है।
4. C से गुजरने वाली किरण AE खींचिए।
5. अब, B को केंद्र और त्रिज्या (= 4 सेमी) लेकर एक वृत्त का चाप खींचिए, जो AX को बिंदु A पर प्रतिच्छेद करता है।
6. A को केन्द्र मानकर तथा चरण 5 की तरह समान त्रिज्या लेकर, पहले खींचे गए चाप को बिन्दु C पर काटते हुए एक चाप खींचिए।
   C से गुजरने वाली किरण BF खींचिए।
   तब, ∆ ABC अभीष्ट त्रिभुज है जिसकी भुजा 4 सेमी है।

औचित्य
AB = BC (रचना से)
AB = AC (रचना से)
∴ AB = BC = CA
∴ ∆ ABC एक समबाहु त्रिभुज है।
∴ रचना औचित्यपूर्ण है।

Ex 11.2

प्रश्न 1.
एक ∆ ABC की रचना कीजिए जिसमें BC = 7 सेमी, ∠B = 75° और AB + AC = 13 सेमी है।
हल:
दिया गया है कि, ∆ ABC में, BC = 7 सेमी, ∠B = 75° और AS + AC = 13 सेमी है।
रचना के चरण

1. आधार BC = 7 सेमी खींचिए
   
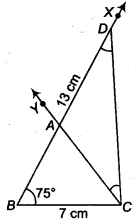
2. बिन्दु 6 पर ∠XBC = 75° बनाइये।
3. किरण BX से AB + AC = 13 सेमी के बराबर एक रेखाखंड BD काटें।
4. डीसी से जुड़ें.
5. ∠DCY = ∠BDC बनाइये।
6. मान लीजिए CY, BX को A पर प्रतिच्छेद करती है।
   तब ABC अभीष्ट त्रिभुज है।

प्रश्न 2.
एक ∆ ABC की रचना कीजिए जिसमें BC = 8 सेमी, ∠B = 45° और AB – AC = 35 सेमी है।
हल:
दिया गया है कि, ∆ ABC में,
BC = 8 सेमी, ∠B = 45° और AB – AC = 3.5 सेमी है।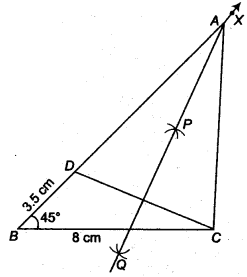

रचना के चरण

1. आधार BC = 8 सेमी खींचिए
2. बिन्दु B पर ∠XBC = 45° बनाइये।
3. किरण BX से AB – AC = 3.5 सेमी के बराबर रेखाखंड BD काटें।
4. डीसी से जुड़ें.
5. DC का लंब समद्विभाजक, मान लीजिए PQ, खींचिए।
6. मान लीजिए कि यह BX को बिंदु A पर प्रतिच्छेद करता है
7. AC को मिलाइये।

प्रश्न 3.
एक ∆ ABC की रचना कीजिए जिसमें QR = 6 सेमी, ∠Q = 60° और PR – PQ = 2 सेमी है।
हल:
दिया गया है कि, ∆ ABC में, QR = 6 सेमी, ∠Q = 60° और PR – PQ = 2 सेमी है।
रचना के चरण

1. आधार QR = 6 सेमी खींचिए
2. बिन्दु Q पर ∠XQR = 60° बनाइये।
3. रेखाखण्ड QR के विपरीत दिशा में बढ़ाई गई रेखा QX से रेखाखण्ड QS = PR-PQ (= 2 सेमी) काटें।
4. एसआर में शामिल हों.
5. SR का लम्ब समद्विभाजक LM खींचिए।
6. मान लीजिए LM, QX को P पर प्रतिच्छेद करता है।
7. पीआर में शामिल हों.
   

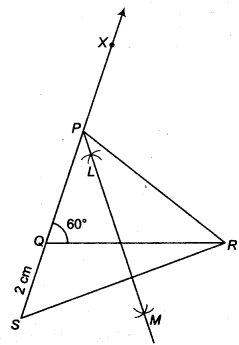
प्रश्न 4.
एक ∆ XYZ की रचना कीजिए जिसमें ∠Y = 30°, ∠Y = 90° तथा XY + YZ + ZX = 11 सेमी है।
हल:
दिया गया है कि, ∆XYZ में ∠Y = 30°, ∠Z = 90° तथा XY + YZ + ZX = 11 सेमी है।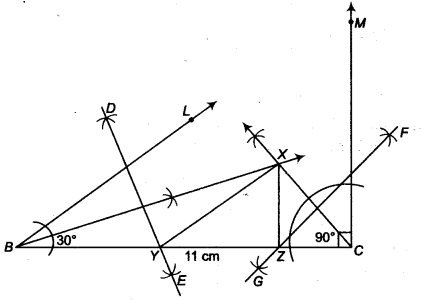

रचना के चरण

1. एक रेखाखंड BC = XY + YZ + ZX = 11 सेमी खींचें
2. ∠LBC = ∠Y = 30° तथा ∠MCB = ∠Z = 90° बनाइये।
3. ∠LBC और ∠MCB को समद्विभाजित कीजिए। मान लीजिए ये समद्विभाजक बिंदु X पर मिलते हैं।
4. XB के लंबवत् समद्विभाजक DE और XC के लंबवत् समद्विभाजक FG खींचिए।
5. मान लीजिए DE, BC को Y पर प्रतिच्छेद करता है तथा FC, BC को Z पर प्रतिच्छेद करता है।
6. XY और XZ को मिलाइए।
   तब, XYZ अभीष्ट त्रिभुज है।

प्रश्न 5.
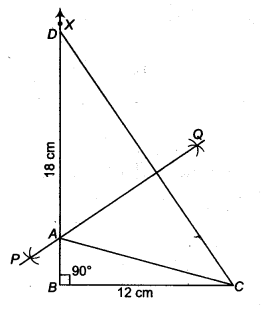
एक समकोण त्रिभुज की रचना कीजिए जिसका आधार 12 सेमी है और कर्ण तथा दूसरी भुजा का योग 18 सेमी है।
हल:
दिया गया है कि त्रिभुज ABC में आधार BC = 12 सेमी, ∠B = 90° और AB + BC = 18 सेमी है।
रचना के चरण

1. आधार BC = 12 सेमी खींचिए
2. बिन्दु 6 पर ∠XBC = 90° बनाइये।
3. किरण BX से 18 सेमी दूरी पर एक रेखाखंड BD = AB + AC = काटें।
4. डीसी से जुड़ें.
5. CD का लंब समद्विभाजक PQ खींचिए जो SD को बिंदु A पर प्रतिच्छेदित करता है

AC को मिलाइए।
तब ABC अभीष्ट समकोण त्रिभुज है।