SikhLo - Current Affairs in Hindi, Daily current affairs, Current affairs

 NCERT Class 9 Maths Chapter 10 वृत्त

NCERT Solutions for Class 9 Maths Chapter 10 वृत्त

Ex 10.1

प्रश्न 1.
रिक्त स्थान भरें।
(i) एक वृत्त का केंद्र वृत्त के ___ में स्थित होता है। (बाहरी/आंतरिक)
(ii) एक बिंदु, जिसकी वृत्त के केंद्र से दूरी उसकी त्रिज्या से अधिक है, वृत्त के ____ में स्थित है, (बाहरी/आंतरिक)
(iii) वृत्त की सबसे लंबी जीवा वृत्त का ____ है।
(iv) एक चाप एक ____ होता है जब उसके सिरे व्यास के सिरे होते हैं।
(v) वृत्त का खंड वृत्त के चाप और ____ के बीच का क्षेत्र होता है।
(vi) एक वृत्त उस तल को, जिस पर वह स्थित है, ____ भागों में विभाजित करता है।
हल:
(i) अभ्यंतर
(ii) बाह्य
(iii) व्यास
(iv) अर्धवृत्त
(v) जीवा
(vi) तीन

प्रश्न 2.
सही या गलत लिखें। अपने उत्तर के लिए कारण दें।
(i) वृत्त पर किसी भी बिंदु को केंद्र से मिलाने वाला रेखाखंड वृत्त की त्रिज्या है।
(ii) एक वृत्त में समान जीवाओं की केवल सीमित संख्या होती है।
(iii) यदि एक वृत्त को तीन बराबर चापों में विभाजित किया जाता है, तो प्रत्येक एक दीर्घ चाप होता है।
(iv) एक वृत्त की एक जीवा, जो इसकी त्रिज्या की दोगुनी लंबी है, वृत्त का एक व्यास है।
(v) त्रिज्यखंड जीवा और इसके संगत चाप के बीच का क्षेत्र है।
(vi) एक वृत्त एक समतल आकृति है।
हल:
(i) सत्य [∵ वृत्त पर सभी बिंदु केंद्र से समान दूरी पर होते हैं]
(ii) असत्य [∵ एक वृत्त में अनंत संख्या में बराबर जीवाएँ हो सकती हैं]
(iii) असत्य [∵ प्रत्येक भाग अर्धवृत्त से छोटा होगा]
(iv) सत्य [∵ व्यास = 2 x त्रिज्या]
(v) असत्य [∵ जीवा और उसके संगत चाप के बीच का क्षेत्र एक वृत्तखंड है]
(vi) सत्य [∵ एक वृत्त एक समतल पर खींचा गया है]

Ex 10.2

प्रश्न 1.
याद कीजिए कि दो वृत्त सर्वांगसम होते हैं, यदि उनकी त्रिज्याएँ समान हों। सिद्ध कीजिए कि सर्वांगसम वृत्तों की समान जीवाएँ अपने केंद्रों पर समान कोण अंतरित करती हैं।
हल:
दिया गया है: केंद्र O और O' तथा त्रिज्याएँ r वाले दो सर्वांगसम वृत्त, जिनकी जीवाएँ क्रमशः AB और CD इस प्रकार हैं कि AB = CD है।
सिद्ध करना है: ∠AOB = ∠CO'D
प्रमाण: ∆AOB और ∆CO'D में,
AB = CD [दिया गया है]
OA = O'C [प्रत्येक बराबर r]
OB = O'D [प्रत्येक बराबर r]
∴ ∆AOB ≅ ∆CO'D [SSS सर्वांगसमता मानदंड से]
⇒ ∠AOB = ∠CO'D [CPCT]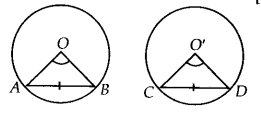

प्रश्न 2.
सिद्ध कीजिए कि यदि सर्वांगसम वृत्तों की जीवाएँ अपने केंद्रों पर समान कोण अंतरित करती हैं, तो जीवाएँ बराबर होती हैं।
हल:
दिया गया है: केंद्र O और O' तथा त्रिज्या r वाले दो सर्वांगसम वृत्त जिनकी जीवाएँ क्रमशः AB और CD इस प्रकार हैं कि ∠AOB = ∠CO'D है।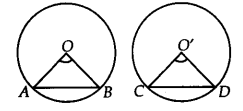

सिद्ध करना है: AB = CD
प्रमाण: ∆AOB और ∆CO'D में,
OA = O'C [प्रत्येक r के बराबर है]
OB = O'D [प्रत्येक r के बराबर है]
∠AOB = ∠CO'D [दिया गया है]
∴ ∆AOB ≅ ∆CO'D [SAS सर्वांगसमता मानदंड से]
अतः, AB = CD [CPCT]

Ex 10.3

प्रश्न 1.
वृत्तों के विभिन्न युग्म बनाएँ। प्रत्येक युग्म में कितने बिंदु उभयनिष्ठ हैं? उभयनिष्ठ बिंदुओं की अधिकतम संख्या कितनी है?
हल:
(i) दो बिंदु उभयनिष्ठ हैं

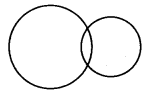
(ii) एक बिंदु उभयनिष्ठ है

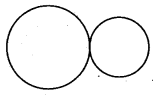
(iii) कोई भी बिंदु उभयनिष्ठ नहीं है

(iv) कोई भी बिंदु उभयनिष्ठ नहीं है

(v) एक बिंदु उभयनिष्ठ है।

आकृतियों से स्पष्ट है कि इन युग्मों में 0, 1 या 2 बिंदु उभयनिष्ठ हो सकते हैं।
अतः वृत्तों का एक युग्म एक-दूसरे को दो से अधिक बिंदुओं पर प्रतिच्छेद नहीं कर सकता।

प्रश्न 2.
मान लीजिए आपको एक वृत्त दिया गया है। इसका केंद्र ज्ञात करने के लिए एक रचना कीजिए।
हल:
रचना के चरण:
चरण I: दिए गए वृत्त पर कोई तीन बिंदु लीजिए। मान लीजिए ये बिंदु A, B और C हैं।
चरण II: AB और BC को मिलाइए।
चरण III: AB का लंब समद्विभाजक PQ खींचिए।
चरण IV: BC का लंब समद्विभाजक RS इस प्रकार खींचिए कि वह PQ को O पर प्रतिच्छेद करे।

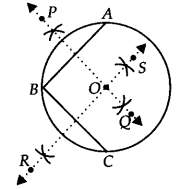
इस प्रकार, 'O' दिए गए वृत्त का अभीष्ट केंद्र है।

प्रश्न 3.
यदि दो वृत्त दो बिंदुओं पर प्रतिच्छेद करते हैं, तो सिद्ध कीजिए कि उनके केंद्र उभयनिष्ठ जीवा के लंब समद्विभाजक पर स्थित हैं।
हल:
हमारे पास O और O' केंद्रों वाले दो वृत्त हैं, जो A और B पर प्रतिच्छेद करते हैं।
∴ AB दो वृत्तों की उभयनिष्ठ जीवा है और OO' उनके केंद्रों को मिलाने वाला रेखाखंड है।
मान लीजिए OO' और AB एक दूसरे को M पर प्रतिच्छेद करते हैं।

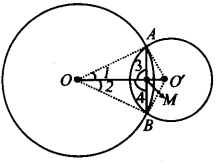
∴ यह सिद्ध करने के लिए कि OO' AB का लंब समद्विभाजक है,
हम OA, OB, O'A और O'B को मिलाते हैं। अब, ∆QAO' और ∆OBO' में,
हमारे पास है
OA = OB [एक ही वृत्त की त्रिज्याएँ]
O'A = O'B [एक ही वृत्त की त्रिज्याएँ]
OO' = OO' [उभयनिष्ठ]
∴ ∆OAO' ≅ ∆OBO' [SSS सर्वांगसमता मानदंड से]
⇒ ∠1 = ∠2, [CPCT]
अब, ∆AOM और ∆BOM में, हमारे पास है
OA = OB [एक ही वृत्त की त्रिज्याएँ]
OM = OM [उभयनिष्ठ]
∠1 = ∠2 [ऊपर सिद्ध]
∴ ∆AOM = ∆BOM [SAS सर्वांगसमता मानदंड से]
⇒ ∠3 = ∠4 [CPCT]
लेकिन ∠3 + ∠4 = 180° [रैखिक युग्म]
∴∠3=∠4 = 90°
⇒ AM ⊥ OO'
साथ ही, AM = BM [CPCT]
⇒ M, AB का मध्य-बिंदु है।
अतः, OO', AB का लंब समद्विभाजक है।

Ex 10.4

प्रश्न 1.
5 सेमी और 3 सेमी त्रिज्याओं वाले दो वृत्त दो बिंदुओं पर प्रतिच्छेद करते हैं और उनके केंद्रों के बीच की दूरी 4 सेमी है। उभयनिष्ठ जीवा की लंबाई ज्ञात कीजिए।
हल:
हमारे पास क्रमशः O और O' केंद्रों वाले दो प्रतिच्छेदी वृत्त हैं। मान लीजिए PQ उभयनिष्ठ जीवा है।
∵ दो प्रतिच्छेदी वृत्तों में, उनके केंद्रों को मिलाने वाली रेखा उभयनिष्ठ जीवा का लंब समद्विभाजक होती है।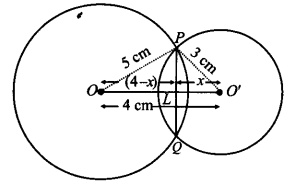

∴ ∠OLP = ∠OLQ = 90° और PL = LQ
अब, समकोण ∆OLP में, हमारे पास है
PL 2 + OL 2 = 2
⇒ PL 2 + (4 – x) 2 = 5 2
⇒ PL 2 = 5 2 – (4 – x) 2
⇒ PL 2 = 25 -16 – x 2 + 8x
⇒ PL 2 = 9 – x 2 + 8x …(i)
पुनः, समकोण ∆O'LP में,
PL 2 = PO '2 – LO '2
= 3 2 – x 2 = 9 – x 2 …(ii)
(i) और (ii) से, हमारे पास है
9 – x 2 + 8x = 9 – x 2
⇒ 8x = 0
⇒ x = 0
⇒ L और O' संपाती हैं।
∴ PQ छोटे वृत्त का व्यास है।
⇒ PL = 3 सेमी
लेकिन PL = LQ
∴ LQ = 3 सेमी
∴ PQ = PL + LQ = 3 सेमी + 3 सेमी = 6 सेमी
इस प्रकार, सामान्य जीवा की आवश्यक लंबाई = 6 सेमी।

प्रश्न 2.
यदि किसी वृत्त की दो बराबर जीवाएँ वृत्त के भीतर प्रतिच्छेद करती हैं, तो सिद्ध कीजिए कि एक जीवा के खंड दूसरी जीवा के संगत खंडों के बराबर होते हैं।
हल:
दिया गया है: केंद्र O वाला एक वृत्त, जिस पर बराबर जीवाएँ AB और CD हैं, E पर प्रतिच्छेद करती हैं।
सिद्ध कीजिए: AE = DE और CE = BE
रचना: OM ⊥ AB और ON ⊥ CD खींचिए।
OE को मिलाइए।
प्रमाण: चूँकि AB = CD [दिया गया है]
∴ OM = ON [समान जीवाएँ केंद्र से समान दूरी पर हैं]
अब, ∆OME और ∆ONE में, हमारे पास है
∠OME = ∠ONE [प्रत्येक 90° के बराबर है]
OM = ON [ऊपर सिद्ध]
OE = OE [उभयनिष्ठ कर्ण]
∴ ∆OME ≅ ∆ONE [RHS सर्वांगसमता मानदंड से]
⇒ ME = NE [CPCT]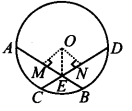

दोनों ओर AM जोड़ने पर, हम पाते हैं
⇒ AM + ME = AM + NE
⇒ AE = DN + NE = DE
∵ AB = CD ⇒ \(\frac { 1 }{ 2 }AB\) = \(\frac { 1 }{ 2 }DC\) ⇒ AM = DN ⇒ AE = DE …(i) अब, AB – AE = CD – DE ⇒ BE = CE …….(ii) (i) और (ii) से, हमें प्राप्त होता है AE = DE और CE = BE12AB = 12DC

प्रश्न 3.
यदि किसी वृत्त की दो बराबर जीवाएँ वृत्त के भीतर प्रतिच्छेद करती हैं, तो सिद्ध कीजिए कि प्रतिच्छेद बिंदु को केंद्र से मिलाने वाली रेखा जीवाओं के साथ समान कोण बनाती है।
हल:
दिया गया है: केंद्र O वाला एक वृत्त जिस पर बराबर जीवाएँ AB और CD हैं, E पर प्रतिच्छेद करती हैं।
सिद्ध करना है: ∠OEA = ∠OED
रचना: OM ⊥ AB और ON ⊥ CD खींचिए।
OE को मिलाइए।
प्रमाण: ∆OME और ∆ONE में,
OM = ON
[समान जीवाएँ केंद्र से समान दूरी पर हैं]
OE = OE [उभयनिष्ठ कर्ण]

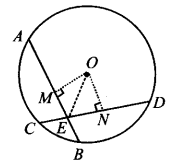
∠OME = ∠ONE [प्रत्येक 90° के बराबर]
∴ ∆OME ≅ ∆ONE [RHS सर्वांगसमता मानदंड से]
⇒ ∠OEM = ∠OEN [CPCT]
⇒ ∠OEA = ∠OED

प्रश्न 4.
यदि एक रेखा दो संकेंद्रित वृत्तों (एक ही केंद्र वाले वृत्त) को केंद्र 0 के साथ A, B, C और D पर प्रतिच्छेद करती है, तो सिद्ध कीजिए कि AB = CD (आकृति देखें)।

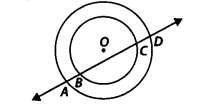
हल:
दिया गया है: दो वृत्त जिनका केंद्र O है।
एक रेखा D बाहरी वृत्त को A और D पर और आंतरिक वृत्त को B और C पर प्रतिच्छेद करती है।
सिद्ध करना है: AB = CD।
रचना:
OM ⊥ l खींचिए।
प्रमाण: बाहरी वृत्त के लिए,
OM ⊥ l [रचना से]
∴ AM = MD …(i)
[केंद्र से जीवा पर लंबवत जीवा को समद्विभाजित करता है]

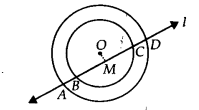
आंतरिक वृत्त के लिए,
OM ⊥ l [रचना से]
∴ BM = MC …(ii)
[केंद्र से जीवा पर लंबवत जीवा को समद्विभाजित करता है]
(ii) को (i) से घटाने पर, हमें
AM – BM = MD – MC
⇒ AB = CD मिलता है

प्रश्न 5.
तीन लड़कियाँ रेशमा, सलमा और मंदीप एक पार्क में खींचे गए 5 मीटर त्रिज्या वाले वृत्त पर खड़ी होकर कोई खेल खेल रही हैं। रेशमा सलमा की ओर गेंद फेंकती है, सलमा मंदीप की ओर, मंदीप रेशमा की ओर। यदि रेशमा और सलमा के बीच तथा सलमा और मंदीप के बीच की दूरी 6 मीटर है, तो रेशमा और मंदीप के बीच की दूरी क्या है?
हल:
मान लीजिए कि तीन लड़कियाँ रेशमा, सलमा और मंदीप केंद्र O और त्रिज्या 5 मीटर वाले वृत्त पर क्रमशः R, S और M पर इस प्रकार स्थित हैं कि
RS = SM = 6 मीटर [दिया गया है]

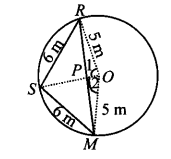
एक वृत्त की बराबर जीवाएँ केंद्र पर बराबर कोण अंतरित करती हैं।
∴ ∠1 = ∠2
∆POR और ∆POM में, हमारे पास है
OP = OP [उभयनिष्ठ]
OR = OM [एक ही वृत्त की त्रिज्याएँ]
∠1 = ∠2 [ऊपर सिद्ध]
∴ ∆POR ≅ ∆POM [SAS सर्वांगसमता मानदंड से]
∴ PR = PM और
∠OPR = ∠OPM [CPCT]
∵∠OPR + ∠OPM = 180° [रैखिक युग्म]
∴∠OPR = ∠OPM = 90°
⇒ OP ⊥ RM
अब, ∆RSP और ∆MSP में, हमारे पास है
RS = MS [प्रत्येक 6 सेमी]
SP = SP [उभयनिष्ठ]
PR = PM [ऊपर सिद्ध]
∴ ∆RSP ≅ ∆MSP [SSS सर्वांगसमता मानदंड से]
⇒ ∠RPS = ∠MPS [CPCT]
लेकिन ∠RPS + ∠MPS = 180° [रैखिक युग्म]
⇒ ∠RPS = ∠MPS = 90°
SP, O से होकर गुजरता है।
माना OP = xm
∴ SP = (5 – x)m
अब, समकोण ∆OPR में, हमारे पास है
x 2 + RP 2 = 5 2
RP 2 = 5 2 – x 2
समकोण ∆SPR में, हमारे पास है
(5 – x) 2 + RP 2 = 6 2
⇒ RP 2 = 6 2 – (5 – x) 2 ……..(ii)
(i) और (ii) से, हम पाते हैं
⇒ 5 2 – x 2 = 6 2 – (5 – x) 2
⇒ 25 – x 2 = 36 – [25 – 10x + x 2 ]
⇒ – 10x + 14 = 0
⇒ 10x = 14 ⇒ x = \(\frac { 14 }{ 10 }\) = 1.41410= 1.4
अब, RP 2 = 5 2 – x 2
⇒ RP 2 = 25 – (1.4) 2
⇒ RP 2 = 25 – 1.96 = 23.04
∴ RP = \(\sqrt { 23.04 }\)= 4.823.04−−−−√= 4.8
∴ RM = 2RP = 2 x 4.8 = 9.6
इस प्रकार, रेशमा और मंदीप के बीच की दूरी 9.6 मीटर है।

Ex 10.5

प्रश्न 1.
आकृति में, A, B और C केंद्र 0 वाले एक वृत्त पर तीन बिंदु इस प्रकार हैं कि ∠BOC = 30° और ∠AOB = 60° है। यदि D, चाप ABC के अलावा वृत्त पर एक अन्य बिंदु है, तो ∠ADC ज्ञात कीजिए।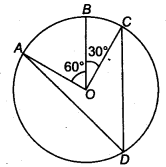

हल:
हमारे पास केंद्र O वाला एक वृत्त है, इस प्रकार है कि
∠AOB = 60° और ∠BOC = 30°
∵∠AOB + ∠BOC = ∠AOC
∴ ∠AOC = 60° + 30° = 90°
एक चाप द्वारा वृत्त पर अंतरित कोण केंद्र पर अंतरित कोण का आधा होता है।
∴ ∠ ADC = \(\frac { 1 }{ 2 }\) (∠AOC) = \(\frac { 1 }{ 2 }\)(90°) = 45°12(∠AOC) =12(90°) = 45°

प्रश्न 2.
एक वृत्त की एक जीवा वृत्त की त्रिज्या के बराबर है। जीवा द्वारा लघु चाप पर एक बिंदु पर और दीर्घ चाप पर एक बिंदु पर अंतरित कोण ज्ञात कीजिए।
हल:
हमारे पास एक वृत्त है जिसकी जीवा AB वृत्त की त्रिज्या के बराबर है।
∴ AO = BO = AB
⇒ ∆AOB एक समबाहु त्रिभुज है।
चूँकि, एक समबाहु त्रिभुज का प्रत्येक कोण 60° का होता है।
⇒ ∠AOB = 60°
चूँकि, चाप ACB वृत्त के केंद्र पर प्रतिवर्ती ∠AOB = 360° – 60° = 300° बनाता है और वृत्त के लघु चाप पर एक बिंदु पर ∠ACB बनाता है।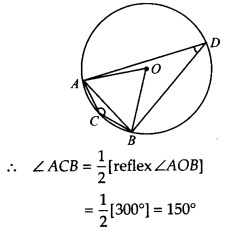

अतः, जीवा द्वारा लघु चाप पर अंतरित कोण = 150° है।
इसी प्रकार, ∠ADB = \(\frac { 1 }{ 2 }\) [∠AOB] = \(\frac { 1 }{ 2 }\) x 60° = 30°12[∠AOB] =12x 60° = 30°
अतः, दीर्घ चाप पर जीवा द्वारा अंतरित कोण = 30°

प्रश्न 3.
आकृति में, ∠PQR = 100° है, जहाँ P, Q और R केंद्र O वाले एक वृत्त पर स्थित बिंदु हैं। ∠OPR ज्ञात कीजिए।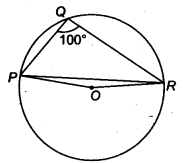

हल:
एक वृत्त के चाप द्वारा उसके केंद्र पर अंतरित कोण उसी चाप द्वारा परिधि पर स्थित बिंदु p पर अंतरित कोण का दोगुना होता है।
∴ प्रतिवर्ती ∠POR = 2∠PQR
लेकिन ∠PQR = 100°
∴ प्रतिवर्ती ∠POR = 2 x 100° = 200°
क्योंकि, ∠POR + प्रतिवर्ती ∠POR = 360°
⇒ ∠POR = 360° – 200°
⇒ ∠POR = 160°
क्योंकि, OP = OR [एक ही वृत्त की त्रिज्याएँ]
∴ ∆POR में, ∠OPR = ∠ORP
[एक त्रिभुज की बराबर भुजाओं के विपरीत कोण बराबर होते हैं]
साथ ही, ∠OPR + ∠ORP + ∠POR = 180°
[एक त्रिभुज के कोणों का योग 180° होता है]
⇒ ∠OPR + ∠ORP + 160° = 180°
⇒ 2∠OPR = 180° -160° = 20° [∠OPR = ∠ORP]
⇒ ∠OPR = \(\frac { { 20 }^{ \circ } }{ 2 } \) = 10°20∘2= 10°

प्रश्न 4.
आकृति में, ∠ABC = 69°, ∠ACB = 31°, ∠BDC ज्ञात कीजिए।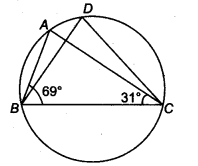

हल:
∆ABC में, ∠ABC + ∠ACB + ∠BAC = 180°
⇒ 69° + 31° + ∠BAC = 180°
⇒ ∠BAC = 180° – 100° = 80°
चूँकि, एक ही वृत्तखंड में कोण बराबर होते हैं।
∴∠BDC = ∠BAC ⇒ ∠BDC = 80°

प्रश्न 5.
आकृति में, A, B और C एक वृत्त पर चार बिंदु हैं। AC और BD एक बिंदु E पर इस प्रकार प्रतिच्छेद करते हैं कि ∠BEC = 130° और ∠ECD = 20° है। ∠BAC ज्ञात कीजिए।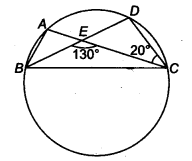

हल:
∠BEC = ∠EDC + ∠ECD
[आंतरिक सम्मुख कोणों का योग बाह्य कोण के बराबर होता है]
⇒ 130° = ∠EDC + 20°
⇒ ∠EDC = 130° – 20° = 110°
⇒ ∠BDC = 110°
चूँकि, एक ही वृत्तखंड में कोण बराबर होते हैं।
∴ ∠BAC = ∠BDC
⇒ ∠BAC = 110°

प्रश्न 6.
ABCD एक चक्रीय चतुर्भुज है जिसके विकर्ण एक बिंदु E पर प्रतिच्छेद करते हैं। यदि ∠DBC = 70°, ∠BAC = 30°, तो ∠BCD ज्ञात कीजिए। इसके अतिरिक्त, यदि AB = BC, तो ∠ECD ज्ञात कीजिए।
हल:
चूँकि एक ही वृत्तखंड के कोण बराबर होते हैं।
∴ ∠BAC = ∠BDC
⇒ ∠BDC = 30°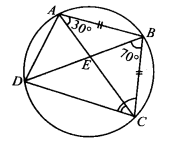

इसी प्रकार, ∠DBC = 70° [दिया गया है]
∆BCD में, हमारे पास है
∠BCD + ∠DBC + ∠CDB = 180° [एक त्रिभुज के कोणों का योग 180° होता है]
⇒ ∠BCD + 70° + 30° = 180°
⇒ ∠BCD = 180° -100° = 80°
अब, ∆ABC में,
AB = BC [दिया गया है]
∴ ∠BCA = ∠BAC [एक त्रिभुज की बराबर भुजाओं के सम्मुख कोण बराबर होते हैं]
⇒ ∠BCA = 30° [∵ ∠B AC = 30°]
अब, ∠BCA + ∠BCD = ∠BCD
⇒ 30° + ∠ECD = 80°
⇒ ∠BCD = 80° – 30° = 50°

प्रश्न 7.
यदि एक चक्रीय चतुर्भुज के विकर्ण उसके शीर्षों से गुजरने वाले वृत्त के व्यास हों, तो सिद्ध कीजिए कि यह एक आयत है।
हल:
चूँकि AC और BD व्यास हैं।
⇒ AC = BD …(i) [वृत्त के सभी व्यास बराबर होते हैं]
साथ ही, ∠BAD = 90° [अर्धवृत्त में बनने वाला कोण 90° होता है]
इसी प्रकार, ∠ABC = 90°, ∠BCD = 90°
और ∠CDA = 90°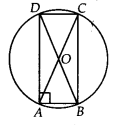

अब, ∆ABC और ∆BAD में, हमारे पास है
AC = BD [(i) से]
AB = BA [उभयनिष्ठ कर्ण]
∠ABC = ∠BAD [प्रत्येक 90° के बराबर]
∴ ∆ABC ≅ ∆BAD [RHS सर्वांगसमता मानदंड से]
⇒ BC = AD [CPCT]
इसी प्रकार, AB = DC
इस प्रकार, चक्रीय चतुर्भुज ABCD ऐसा है कि इसकी विपरीत भुजाएँ बराबर हैं और इसका प्रत्येक कोण समकोण है।
∴ ABCD एक आयत है।

प्रश्न 8.
यदि किसी समलम्ब चतुर्भुज की असमान्तर भुजाएँ बराबर हों, तो सिद्ध कीजिए कि वह चक्रीय है।
हल:
हमारे पास एक समलम्ब चतुर्भुज ABCD है जिसमें AB ॥ CD और AD = BC है।
आइए BE ॥ AD इस प्रकार खींचें कि ABED एक समांतर चतुर्भुज हो।
∵ एक समांतर चतुर्भुज के सम्मुख कोण और सम्मुख भुजाएँ बराबर होती हैं।
∴ ∠BAD = ∠BED …(i)
और AD = BE …(ii)
लेकिन AD = BC [दिया है] …(iii)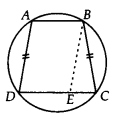

∴ (ii) और (iii) से, हमारे पास है BE = BC
⇒ ∠BCE = ∠BEC … (iv) [एक त्रिभुज की बराबर भुजाओं के विपरीत कोण बराबर होते हैं]
अब, ∠BED + ∠BEC = 180° [रैखिक युग्म]
⇒ ∠BAD + ∠BCE = 180° [(i) और (iv) का उपयोग करके]
यानी, चतुर्भुज ABCD के विपरीत कोणों की एक जोड़ी 180° है।
∴ ABCD चक्रीय है।
⇒ समलम्ब चतुर्भुज ABCD चक्रीय है।

प्रश्न 9.
दो वृत्त दो बिंदुओं B और C पर प्रतिच्छेद करते हैं। B से होकर दो रेखाखंड ABD और PBQ खींचे गए हैं जो वृत्तों को क्रमशः A,D और P, Q पर प्रतिच्छेद करते हैं (आकृति देखें)। सिद्ध कीजिए कि ∠ ACP = ∠QCD।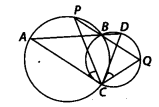

हल:
चूँकि, एक ही वृत्तखंड के कोण बराबर होते हैं।
∴ ∠ACP = ∠ABP …(i)
इसी प्रकार, ∠QCD = ∠QBD …(ii)
चूँकि, ∠ABP = ∠QBD …(iii) [शीर्षाभिमुख कोण]
∴ (i), (ii) और (iii) से, हमें प्राप्त है
∠ACP = ∠QCD

प्रश्न 10.
यदि किसी त्रिभुज की दो भुजाओं को व्यास मानकर वृत्त खींचे जाते हैं, तो सिद्ध कीजिए कि इन वृत्तों का प्रतिच्छेद बिंदु तीसरी भुजा पर स्थित होता है।
हल:
हमारे पास ∆ABC है, और दो वृत्त हैं जिनके व्यास क्रमशः AB और AC हैं। वे A के अलावा किसी अन्य बिंदु D पर प्रतिच्छेद करते हैं।
आइए A और D को मिलाएँ।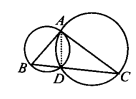

∵ AB एक व्यास है।
∴∠ADB अर्धवृत्त में बना कोण है।
⇒ ∠ADB = 90° ……(i)
इसी प्रकार, ∠ADC = 90° ….(ii)
(i) और (ii) को जोड़ने पर, हमारे पास
∠ADB + ∠ADC = 90° + 90° = 180° है
अर्थात, B, D और C संरेख बिंदु हैं।
⇒ BC एक सरल रेखा है। इस प्रकार, D, BC पर स्थित है।

प्रश्न 11.
ABC और ADC दो समकोण त्रिभुज हैं जिनका कर्ण AC उभयनिष्ठ है। सिद्ध कीजिए कि ∠CAD = ∠CBD है।
हल:
∆ABC और ∆ADC इस प्रकार हैं कि इनका कर्ण AC उभयनिष्ठ है और ∠ADC = 90° = ∠ABC है
। ∴ दोनों त्रिभुज अर्धवृत्त में हैं।

स्थिति - I: यदि दोनों त्रिभुज एक ही अर्धवृत्त में हैं।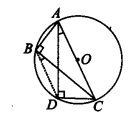

⇒ A, B, C और D चक्रीय हैं।
BD को मिलाएँ।
DC एक जीवा है।
∴ ∠CAD और ∠CBD एक ही वृत्तखंड में बनते हैं।
⇒ ∠CAD = ∠CBD

स्थिति - II : यदि दोनों त्रिभुज एक ही अर्धवृत्त में नहीं हैं।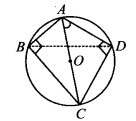

⇒ A, B, C और D चक्रीय हैं। BD को मिलाएँ। DC एक जीवा है।
∴ ∠CAD और ∠CBD एक ही वृत्तखंड में बनते हैं।
⇒ ∠CAD = ∠CBD

प्रश्न 12.
सिद्ध कीजिए कि एक चक्रीय समांतर चतुर्भुज एक आयत होता है।
हल:
हमारे पास एक चक्रीय समांतर चतुर्भुज ABCD है। चूँकि, ABCD एक चक्रीय चतुर्भुज है।
∴ इसके सम्मुख कोणों का योग 180° होता है।
⇒ ∠A + ∠C = 180° …(i)
लेकिन ∠A = ∠C …(ii)
[समांतर चतुर्भुज के सम्मुख कोण बराबर होते हैं]
(i) और (ii) से, हमें प्राप्त है
∠A = ∠C = 90°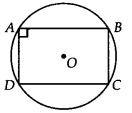

इसी प्रकार,
∠B = ∠D = 90°
⇒ समांतर चतुर्भुज ABCD का प्रत्येक कोण 90° है।
इस प्रकार, ABCD एक आयत है।

Ex 10.6

प्रश्न 1.
सिद्ध कीजिए कि दो प्रतिच्छेदी वृत्तों की केन्द्र रेखा उनके प्रतिच्छेद बिंदुओं पर समान कोण अंतरित करती है।
हल:
दिया गया है: दो वृत्त जिनके केन्द्र क्रमशः O और O' हैं इस प्रकार हैं कि वे एक दूसरे को P और Q पर प्रतिच्छेद करते हैं।
सिद्ध करना है: ∠OPO' = ∠OQO'।
रचना: OP, O'P, OQ, O'Q और OO' को मिलाइए।
उपपत्ति: ∆OPO' और ∆OQO' में,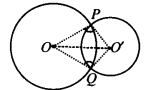

OP = OQ [एक ही वृत्त की त्रिज्याएँ]
O'P = O'Q [एक ही वृत्त की त्रिज्याएँ]
OO' = OO' [उभयनिष्ठ]
∴ AOPO' = AOQO' [SSS सर्वांगसमता मानदंड से]
⇒ ∠OPO' = ∠OQO' [CPCT]

प्रश्न 2.
एक वृत्त की क्रमशः 5 सेमी और 11 सेमी लंबाई की दो जीवाएँ AB और CD एक दूसरे के समानांतर हैं और इसके केंद्र के विपरीत दिशाओं में हैं। यदि AB और CD के बीच की दूरी 6 सेमी है, तो वृत्त की त्रिज्या ज्ञात कीजिए।
हल:
हमारे पास केंद्र O वाला एक वृत्त है।
AB || CD और AB और CD के बीच लंबवत दूरी 6 सेमी है और AB = 5 सेमी, CD = 11 सेमी है।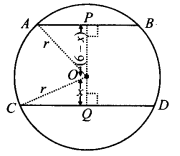

माना r सेमी वृत्त की त्रिज्या है।
आइए OP ⊥ AB और OQ ⊥ CD इस प्रकार खींचें कि
PQ = 6 सेमी
OA और OC को मिलाएं।
माना OQ = x सेमी
∴ OP = (6 – x) सेमी
∵ एक वृत्त के केंद्र से जीवा पर डाला गया लंब जीवा को समद्विभाजित करता है।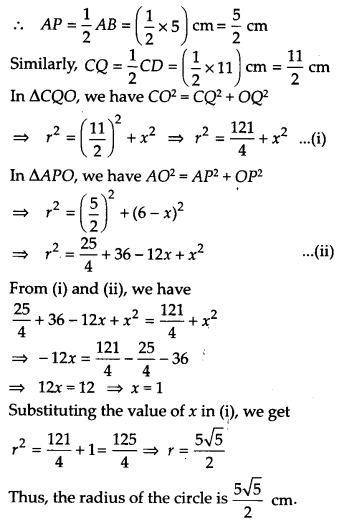

प्रश्न 3.
ABCD एक समांतर चतुर्भुज है। A, B और C से होकर जाने वाला वृत्त CD (यदि आवश्यक हो तो बढ़ाएँ) को E पर प्रतिच्छेद करता है। सिद्ध कीजिए कि AE = AD।
हल:
A, B और C से होकर जाने वाला एक वृत्त इस प्रकार खींचा गया है कि वह CD को E पर प्रतिच्छेद करता है।
ABCE एक चक्रीय चतुर्भुज है।
∴∠AEC + ∠B = 180° …(i)
[चक्रीय चतुर्भुज के सम्मुख कोण संपूरक होते हैं] लेकिन ABCD एक समांतर चतुर्भुज है। [दिया गया है]
∴∠D = ∠B …(ii)
[समानांतर चतुर्भुज के सम्मुख कोण बराबर होते हैं]
(i) और (ii) से, हमें मिलता है
∠AEC + ∠D = 180° …(iii)
लेकिन ∠AEC + ∠AED = 180° [रैखिक युग्म] …(iv)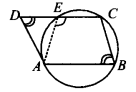

(iii) और (iv) से, हमें मिलता है ∠D = ∠AED
अर्थात, AADE के आधार कोण बराबर हैं।
∴ सम्मुख भुजाएँ बराबर होनी चाहिए।
⇒ AE = AD

प्रश्न 4.
AC और BD एक वृत्त की जीवाएँ हैं जो एक दूसरे को समद्विभाजित करती हैं। सिद्ध कीजिए कि
(i) AC और BD व्यास हैं,
(ii) ABCD एक आयत है।
हल:
दिया गया है: एक वृत्त जिसमें दो जीवाएँ AC और BD इस प्रकार हैं कि वे एक दूसरे को समद्विभाजित करती हैं। मान लीजिए उनका प्रतिच्छेद बिंदु 0 है।
सिद्ध कीजिए: (i) AC और BD व्यास हैं।
(ii) ABCD एक आयत है।
रचना: AB, BC, CD और DA को मिलाइए।
प्रमाण: (i) ∆AOB और ∆COD में, हमारे पास है
AO = CO [O, AC का मध्य-बिंदु है]
BO = DO [O, BD का मध्य-बिंदु है]
∠AOB = ∠COD [ऊर्ध्वाधर विपरीत कोण]
∴ सर्वांगसमता के SAS मानदंड का उपयोग करते हुए,
∆AOB ≅ ∆COD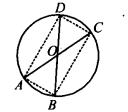

⇒ AB = CD [CPCT]
⇒ चाप AB = चाप CD …(1)
इसी प्रकार, चाप AD = चाप BC …(2)
(1) और (2) को जोड़ने पर, हम पाते हैं
चाप AB + चाप AD = चाप CD + चाप BC
⇒ 
⇒ BD वृत्त को दो बराबर भागों में विभाजित करता है।
∴ BD एक व्यास है।
इसी प्रकार, AC एक व्यास है।

(ii) हम जानते हैं कि ∆AOB ≅ ∆COD
⇒ ∠OAB = ∠OCD [CPCT]
⇒ ∠CAB = ∠ACD
AB || DC
इसी प्रकार, AD || BC
∴ ABCD एक समांतर चतुर्भुज है।
चूँकि, समांतर चतुर्भुज के सम्मुख कोण बराबर होते हैं।
∴ ∠DAB = ∠DCB
लेकिन ∠DAB + ∠DCB = 180°
[एक चक्रीय चतुर्भुज के सम्मुख कोणों का योग 180° होता है]
⇒ ∠DAB = 90° = ∠DCB इस प्रकार, ABCD एक आयत है।

प्रश्न 5.
दो सर्वांगसम वृत्त एक दूसरे को बिंदु A और B पर प्रतिच्छेद करते हैं। A से होकर एक रेखाखंड PAQ खींचा गया है जिससे P, Q दोनों वृत्तों पर स्थित हैं। सिद्ध कीजिए कि BP = BQ।
हल:
हमारे पास दो सर्वांगसम वृत्त हैं जिससे वे एक दूसरे को A और B पर प्रतिच्छेद करते हैं। A से गुजरने वाला एक रेखाखंड वृत्तों को P और Q पर मिलता है।
आइए हम उभयनिष्ठ जीवा AB खींचते हैं।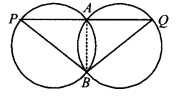

चूँकि सर्वांगसम वृत्तों में समान जीवाओं द्वारा अंतरित कोण बराबर होते हैं।
⇒ ∠APB = ∠AQB
अब, ∆PBQ में, ∠AQB = ∠APB है।
अतः, उनकी सम्मुख भुजाएँ बराबर होनी चाहिए।
⇒ BP = BQ।

प्रश्न 6.
किसी ∆ ABC में, यदि ∠A का कोण समद्विभाजक और BC का लंब समद्विभाजक प्रतिच्छेद करते हैं, तो सिद्ध कीजिए कि वे ∆ ABC के परिवृत्त पर प्रतिच्छेद करते हैं।
हल:
∆ ABC जिसके परिवृत्त का केंद्र O है। BC का लंब समद्विभाजक O से होकर जाता है। OB और OC को मिलाइए। मान लीजिए यह परिवृत्त को P पर काटता है। यह
सिद्ध करने के लिए कि BC का लंब समद्विभाजक और ∆ ABC के कोण A का समद्विभाजक P पर प्रतिच्छेद करते हैं, यह दर्शाना पर्याप्त है कि AP, ∆ ABC के ∠A का समद्विभाजक है।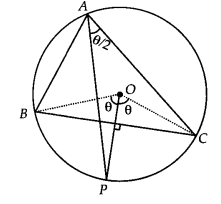

चाप BC परिधि पर कोण θ बनाता है
∴ ∠BOC = 2θ
[केंद्र पर कोण परिधि पर चाप द्वारा बनाए गए कोण का दोगुना है]
साथ ही, ∆ BOC में, OB=OC और OP, BC का लंब समद्विभाजक है।
अतः, ∠BOP = ∠COP = θ चाप CP, O पर कोण θ बनाता है, इसलिए यह परिधि पर कोण [/latex]\frac { \theta }{ 2 }[/latex]
बनाएगा । अतः, ∠COP = [/latex]\frac { \theta }{ 2 }[/latex] अतः, AP, ∆ABC के ∠A का कोण द्विभाजक है।