SikhLo - Current Affairs in Hindi, Daily current affairs, Current affairs

 NCERT Class 9 Maths Chapter 9 समान्तर चतुर्भुज और त्रिभुजों के क्षेत्रफल

NCERT Solutions for Class 9 Maths Chapter 9 समान्तर चतुर्भुज और त्रिभुजों के क्षेत्रफल

Ex 9.1

प्रश्न 1:

निम्नलिखित में से कौन-सी आकृतियाँ एक ही आधार पर और एक ही समान्तर रेखाओं के बीच स्थित हैं। ऐसी स्थिति में, उभयनिष्ठ आधार और दो समान्तर रेखाएँ लिखिए।

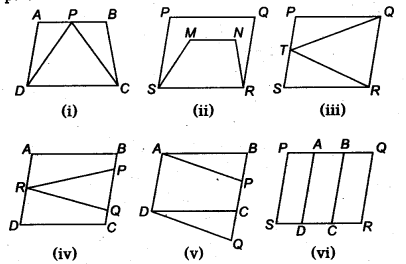
हल:
आकृति (i) में, APDC और समलम्ब चतुर्भुज ABCD एक ही आधार DC पर और समान्तर रेखाओं AB और DC के बीच स्थित हैं।
आकृति (iii) में, ATRO और समांतर चतुर्भुज PQRS एक ही आधार RQ पर स्थित हैं और समान्तर रेखाओं RQ और SP के बीच स्थित हैं।
आकृति (v) में, चतुर्भुज APCD और चतुर्भुज ABQD एक ही आधार AD पर और समान्तर रेखाओं AD और BQ के बीच स्थित हैं।

Ex 9.2

प्रश्न 1.
आकृति में, ABCD एक समांतर चतुर्भुज है, AE ⊥ DC और CF ⊥ AD है। यदि AB = 16 सेमी, AE = 8 सेमी और CF = 10 सेमी है, तो AD ज्ञात कीजिए।

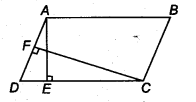
हल:
हम जानते हैं कि,
समांतर चतुर्भुज का क्षेत्रफल = आधार x ऊँचाई
दिया गया है, AE = 8 सेमी CF = 10 सेमी और AB = 16 सेमी
∴ ar (समांतर चतुर्भुज ABCD) = DC x AE
= 16 x 8 cm2 (∵ AE = 8 सेमी)…(i)
और ar (समांतर चतुर्भुज ABCD) = AD x CF – AD x 10 (∵ CF = 10 सेमी)
समीकरण (i) से, हमें मिलता है,
16 x 8 = AD x 10

Ex 9.3

प्रश्न 1.
आकृति में, E एक ∆ABC की माध्यिका AD पर स्थित कोई बिंदु है। दर्शाइए कि ar (ABE) = ar (ACE)।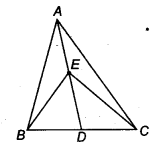

हल:
हमारे पास एक ∆ABC है जिससे AD एक माध्यिका है।
∴ ar(∆ABD) = ar(∆ACD) …(1)
[∵ एक माध्यिका त्रिभुज को बराबर क्षेत्रफलों वाले दो त्रिभुजों में विभाजित करती है]
इसी प्रकार, ∆BEC में, हमारे पास
ar(∆BED) = ar(∆DEC) …(2)
(1) में से (2) घटाने पर, हमारे पास
ar(∆ABD) – ar(∆BED) = ar(∆ACD) – ar(∆DEC)
⇒ ar(∆ABE) = ar(∆ACE) है।

प्रश्न 2.
एक त्रिभुज ABC में, E माध्यिका AD का मध्य-बिंदु है। दर्शाइए कि ax (BED) =12ar(ABC)
हल: हमारे
पास एक ∆ABC और इसकी माध्यिका AD है।
आइए B और E को मिलाएँ।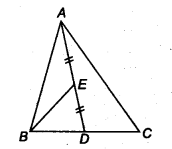

चूँकि एक माध्यिका त्रिभुज को बराबर क्षेत्रफल वाले दो त्रिभुजों में विभाजित करती है।
ar (∆ABD) = 12ar(ΔABC) …….(1)
Now, in ∆ABD, BE is a median.
[ ∵ E is the mid-point of AD]
∴ ar(∆BED) = 12ar(ΔABC) …(2)
From (1) and (2), we have
ar(∆BED) = 12 [12ar(ΔABC) ]
⇒ ar(∆BED) = 14ar(ΔABC)

प्रश्न 3.
दर्शाइए कि एक समांतर चतुर्भुज के विकर्ण उसे बराबर क्षेत्रफल वाले चार त्रिभुजों में विभाजित करते हैं।
हल:
हमारे पास एक समांतर चतुर्भुज ABCD (मान लीजिए) है
जिससे इसके विकर्ण बिंदु O पर प्रतिच्छेद करते हैं।
∵एक समांतर चतुर्भुज के विकर्ण एक दूसरे को समद्विभाजित करते हैं।
∴ AO = OC और BO = OD।
आइए CE ⊥ BD बनाएँ।
अब, ar(∆BOC) =12BO x CE और
ar(∆DOC) =12OD x CE

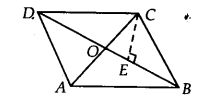
चूंकि, BO = OD
∴ ar(∆BOC) = ar(∆DOC) …(1)
इसी प्रकार, ar(∆AOD) = ar(∆DOC) …(2)
और ar(∆AOB) = ar(∆BOC) …(3)
(1), (2) और (3) से, हमें प्राप्त होता है
ar(∆AOB) = ar(∆BOC) = ar(∆COD) = ar(∆DOA)
इस प्रकार, एक समांतर चतुर्भुज के विकर्ण इसे समान क्षेत्रफल वाले चार त्रिभुजों में विभाजित करते हैं।

प्रश्न 4.
आकृति में, ABC और ABD एक ही आधार AB पर स्थित दो त्रिभुज हैं। यदि रेखाखंड CD, AB द्वारा बिंदु O पर समद्विभाजित होता है, तो दर्शाइए कि ar(ABC) = ar(ABD)

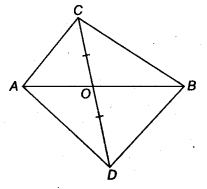
हल:
∆ABC और ∆ABD एक ही आधार AB पर स्थित हैं।
∵ CD, O पर समद्विभाजित होती है। [दिया है]
∴ CO = OD
अब, ∆ACD में, AO एक माध्यिका है
∴ ar(∆OAC) = ar(∆OAD) …(1)
पुनः, ∆BCD में, BO एक माध्यिका है
∴ ar(∆OBC) = ar(∆ODB) …(2)
(1) और (2) को जोड़ने पर, हमारे पास है
ar(∆OAQ + ar(∆OBQ) = ar(∆OAD) + ar(∆ODB)
⇒ ar(∆ABC) = ar(∆ABD)

प्रश्न 5.
D, E और F क्रमशः एक ∆ABC की भुजाओं BC, CA और AB के मध्य-बिंदु हैं। दर्शाइए कि
(i) BDEF एक समांतर चतुर्भुज है।
(ii) ar(DEF) =14ar (ABC)
(iii) ar(BDEF) =14ar (ABC)

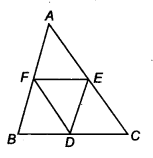
हल:
हमारे पास ∆ABC है जिससे
D,E और F क्रमशः BC, CA और AB के मध्य-बिंदु हैं।

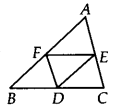
(i) ∆ABC में, E और F क्रमशः AC और BDC AB के मध्य-बिंदु हैं।
∴ EF || BC [मध्य-बिंदु प्रमेय]
⇒ EF || BD
साथ ही, EF =12(BC)
⇒ EF = BD [D, BC का मध्य-बिंदु है]
चूँकि BDEF एक चतुर्भुज है जिसकी सम्मुख भुजाओं का एक युग्म समांतर और समान लंबाई का है।
∴ BDEF एक समांतर चतुर्भुज है।

(ii) हमने सिद्ध किया है कि BDEF एक समांतर चतुर्भुज है।
इसी प्रकार, DCEF एक समांतर चतुर्भुज है और DEAF भी एक समांतर चतुर्भुज है।
अब, समांतर चतुर्भुज BDEF और समांतर चतुर्भुज DCEF एक ही आधार EF पर और समान समांतर रेखाओं BC और EF के बीच स्थित हैं।
∴ ar(|| gm BDEF) = ar(|| gm DCEF)
⇒12ar(|| ग्राम BDEF) =12ar(|| gm DCEF)
⇒ ar(∆BDF) = ar(∆CDE) …(1)
[एक समांतर चतुर्भुज का विकर्ण उसे बराबर क्षेत्रफल वाले दो त्रिभुजों में विभाजित करता है]
इसी प्रकार, ar(∆CDE) = ar(∆DEF) …(2)
और ar(∆AEF) = ar(∆DEF) …(3)
(1), (2) और (3) से, हमारे पास है
ar(∆AEF) = ar(∆FBD) = ar(∆DEF) = ar(∆CDE)
इस प्रकार, ar(∆ABC) = ar(∆AEF) + ar(∆FBD) + ar(∆DEF) + ar(∆CDE) = 4 ar(∆DEF)
⇒ ar(∆DEF) =14ar(∆ABC)

(iii) हमारे पास है, ar (|| gm BDEF) = ar(∆BDF) + ar(∆DEF)
= ar(∆DEF) + ar(∆DEF) [∵ ar(∆DEF) = ar(∆BDF)]
2ar(∆DEF) = 2[14ar(∆ABC)]
=12ar(∆ABC)
इस प्रकार, ar (|| gm BDEF) =12ar(∆ABC)

प्रश्न 6.
आकृति में, चतुर्भुज ABCD के विकर्ण AC और BD बिंदु 0 पर इस प्रकार प्रतिच्छेद करते हैं कि OB = OD है। यदि AB = CD है, तो दर्शाइए कि
(i) ar(DOC) = ar(AOB)
(ii) ar (DCB) = ar (ACB)
(iii) DA || CB या ABCD एक समांतर चतुर्भुज है।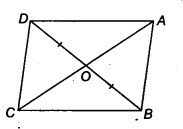

हल:
हमें एक चतुर्भुज ABCD मिला है जिसके विकर्ण AC और BD बिंदु 0 पर प्रतिच्छेद करते हैं।
हमें यह भी प्राप्त है कि OB = OD, AB = CD है। आइए DE ⊥ AC और BF ⊥ AC बनाएँ।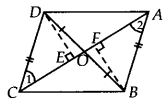

(i) ∆DEO और ∆BFO में,
DO = BO [दिया गया है]
∠DOE = ∠BOF [ऊर्ध्वाधर विपरीत कोण]
∠DEO = ∠BFO [प्रत्येक 90°]
∴ ∆DEO ≅ ∆BFO [A AS सर्वांगसमता से]
⇒ DE = BF [CPCT से]
और ar(∆DEO) = ar(∆BFO) …(1)
अब, ∆DEC और ∆BFA में, ∠DEC
= ∠BFA [प्रत्येक 90°]
DE = BF [ऊपर सिद्ध]
DC = BA [दिया गया है]
∴ ∆DEC ≅ ∆BFA [दाहिनी ओर सर्वांगसमता से]
⇒ ar(∆DEC) = ar(∆BFA) …(2)
और ∠1 = ∠2 …(3) [CPCT द्वारा]
(1) और (2) को जोड़ने पर, हमारे पास
ar(∆DEO) + ar(∆DEC) = ar(∆BFO) + ar(∆BFA) है
⇒ ar(∆DOC) = ar(∆AOB)

(ii) चूँकि, ar(∆DOC) = ar(∆AOB) [ऊपर सिद्ध]
दोनों पक्षों में ar(∆BOC) जोड़ने पर, हमारे पास
ar(∆DOC) + ar(∆BOC) = ar(∆AOB) + ar(∆BOC) है
⇒ ar(∆DCB) = ar(∆ACB)

(iii) चूँकि, ∆DCS और ∆ACB दोनों एक ही आधार CB पर स्थित हैं और उनके क्षेत्रफल समान हैं।
∴ वे समान्तर रेखाओं CB और DA के बीच स्थित हैं।
⇒ CB || DA
साथ ही ∠1 = ∠2, [(3) से]
जो एकांतर अंतः कोण हैं।
अतः, AB || CD
अतः, ABCD एक समांतर चतुर्भुज है।

प्रश्न 7.
D और E क्रमशः ∆ ABC की भुजाओं AB और AC पर स्थित बिंदु इस प्रकार हैं कि ar (DBC) = ar (EBC)। सिद्ध कीजिए कि DE || BC है।
हल:
∆ABC है और बिंदु D और E इस प्रकार हैं कि ar(DBC) = ar{EBC) है।
चूँकि ∆DBC और ∆EBC एक ही आधार BC पर हैं और उनका क्षेत्रफल समान है।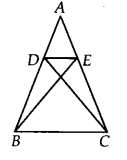

∴ वे समान्तर रेखाओं DE और BC के बीच स्थित होने चाहिए।
अतः, DE || BC

प्रश्न 8.
AB || DC वाले समलम्ब चतुर्भुज ABCD के विकर्ण AC और BD एक दूसरे को बिंदु O पर प्रतिच्छेद करते हैं। सिद्ध कीजिए कि ar (AOD) = ar (BOC)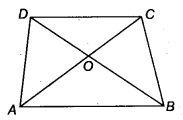

हल:
BBlliWWp में एक समलम्ब चतुर्भुज ABCD है जिसमें AB || CD है तथा इसके विकर्ण AC और BD एक दूसरे को बिंदु O पर प्रतिच्छेद करते हैं।
चूँकि, एक ही आधार पर और एक ही समान्तर रेखाओं के बीच स्थित त्रिभुजों के क्षेत्रफल समान होते हैं।
∆ABD और ∆ABC एक ही आधार AB पर और एक ही समान्तर रेखाओं AB और DC के बीच में हैं
∴ ar(∆ABD) = ar(∆ABC)
दोनों पक्षों से ar(∆AOB) घटाने पर, हम पाते हैं

ar(∆ABD) – ar(∆AOB) = ar(∆ABC) – ar(∆AOB)
⇒ ar(∆AOD) = ar(∆BOC)

प्रश्न 9.
आकृति में, ABCDE एक पंचभुज है। B से AC के समांतर खींची गई एक रेखा, बढ़ाई गई DC को F पर मिलती है। दर्शाइए कि
(i) ar (ACB) = ar (ACF)
(ii) ar (AEDF) = ar (ABCDE)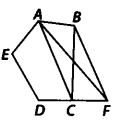

हल:
हमारे पास एक पंचभुज ABCDE है जिसमें BF || AC है और DC को F तक बढ़ाया गया है।
(i) चूँकि, समान समांतर रेखाओं और समान आधार पर स्थित त्रिभुजों का क्षेत्रफल बराबर होता है।
∆ACB और ∆ACF एक ही आधार AC पर और समान समांतर रेखाओं AC और BF के बीच स्थित हैं।
∴ ar(∆ACB) = ar(∆ACF)

(ii) चूँकि, ar(∆ACB) = ar(∆ACF) [ऊपर सिद्ध]
दोनों पक्षों में ar(quad. AEDC) जोड़ने पर, हम पाते हैं
⇒ ar(∆ACB) + ar(quad. AEDC) = ar(∆ACF) + ar(quad. AEDC)
∴ ar(ABCDE) = ar(AEDF)

प्रश्न 10.
इतवारी नामक एक ग्रामीण के पास चतुर्भुज के आकार का एक भूखंड है। गाँव की ग्राम पंचायत ने स्वास्थ्य केंद्र बनाने के लिए उसके भूखंड के एक कोने से कुछ भाग लेने का निर्णय लिया। इतवारी उपरोक्त प्रस्ताव से इस शर्त पर सहमत है कि उसे उसके भूखंड से लगी हुई भूमि के बदले में उतनी ही भूमि दी जाए जिससे एक त्रिभुजाकार भूखंड बने। बताइए कि यह प्रस्ताव कैसे क्रियान्वित किया जाएगा।
हल:
हमारे पास चतुर्भुज ABCD के आकार का एक भूखंड है।
आइए DF || AC खींचें और AF और CF को मिलाएँ।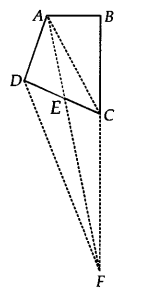

अब, ∆DAF और ∆DCF एक ही आधार DF पर और समान्तर रेखाओं AC और DF के बीच स्थित हैं।
∴ ar(ADAF) = ar(ADCF)
दोनों पक्षों से ar(∆DEF) घटाने पर, हम पाते हैं
ar(∆DAF) – ar(∆DEF) = ar(∆DCF) – ar(∆DEF)
⇒ ar(∆ADE) = ar(∆CEF)
∆ADE का हिस्सा ग्राम पंचायत द्वारा भूमि (∆CEF) को उसकी (इतवारी) भूमि में जोड़कर इस प्रकार लिया जा सकता है कि एक त्रिकोणीय भूखंड,
अर्थात ∆ABF बन जाए।
आइए सिद्ध करें कि ar(∆ABF) = ar(quad. ABCD), हमारे पास है
ar(ACEF) = ar(AADE) [ऊपर सिद्ध]
दोनों पक्षों में ar(quad. ABCE) जोड़ने पर, हम पाते हैं
ar(∆CEF) + ar(quad. ABCE) = ar(∆ADE) + ar (quad. ABCE)
⇒ ar(∆ABF) = ar (quad. ABCD)

प्रश्न 11.
ABCD एक समलम्ब चतुर्भुज है जिसमें AB || DC है। AC के समांतर एक रेखा AB को X पर और BC को Y पर प्रतिच्छेद करती है। सिद्ध कीजिए कि ar(ADX) = ar(ACY)। [संकेत IX को मिलाएँ]
हल:
हमारे पास एक समलम्ब चतुर्भुज ABCD है जिससे AB || DC है।
XY || AC, AB को X पर और BC को Y पर मिलती है। आइए CX को मिलाएँ।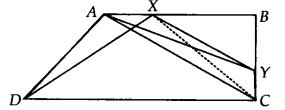

∆ADX और ∆ACX एक ही आधार AX पर और समान्तर रेखाओं AX और DC के बीच हैं।
∴ ar(∆ADX) = ar(∆ACX) …(1)
∵∆ACX और ∆ACY एक ही आधार AC पर और समान्तर रेखाओं AC और XY के बीच हैं।
∴ ar(∆ACX) = ar(∆ACY) …(2)
(1) और (2) से, हमें प्राप्त होता है
ar(∆ADX) = ar(∆ACY)

प्रश्न 12.
आकृति में, AP || BQ || CR. सिद्ध कीजिए कि ar(AQC) = ax(PBR).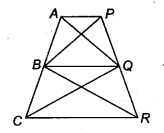

हल:
AP || BQ || CR
∵ ∆BCQ और ∆BQR एक ही आधार BQ पर और समान्तर रेखाओं BQ और CR के बीच स्थित हैं।
∴ ar(∆BCQ) = ar(∆BQR) …(1)
∵ ∆ABQ और ∆PBQ एक ही आधार BQ पर और समान्तर रेखाओं AP और BQ के बीच स्थित हैं।
∴ ar(∆ABQ) = ar(∆PBQ) …(2)
(1) और (2) को जोड़ने पर, हमारे पास है
ar(∆BCQ) + ar(∆ABQ) = ar(∆BQR) + ar(∆PBQ)
⇒ ar(∆AQC) = ar(∆PBR)

प्रश्न 13.
चतुर्भुज ABCD के विकर्ण AC और BD बिंदु 0 पर इस प्रकार प्रतिच्छेद करते हैं कि ax(AOD) = ar(BOC) है। सिद्ध कीजिए कि ABCD एक समलम्ब चतुर्भुज है।
हल:
हमारे पास एक चतुर्भुज ABCD है और इसके विकर्ण AC और BD बिंदु O पर इस प्रकार प्रतिच्छेद करते हैं कि
ar(∆AOD) = ar(∆BOC) [दिया है]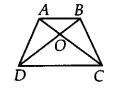

दोनों पक्षों में ar(∆AOB) जोड़ने पर,
ar(∆AOD) + ar(∆AOB) = ar(∆BOC) + ar(∆AOB)
⇒ ar(∆ABD) = ar(∆ABC)
साथ ही, वे एक ही आधार AB पर हैं।
चूँकि, त्रिभुज एक ही आधार पर हैं और समान क्षेत्रफल के हैं।
∴ वे समान्तर रेखाओं के बीच स्थित होने चाहिए।
∴ AB || अब, ABCD
एक चतुर्भुज है जिसमें सम्मुख भुजाओं का एक युग्म समांतर है।
अतः, ABCD एक समलम्ब चतुर्भुज है।

प्रश्न 14.
आकृति में ax(DRC) = ar(DPC) और ai(BDP) = ar(ARC) है। दर्शाइए कि दोनों चतुर्भुज ABCD और DCPR समलम्ब हैं।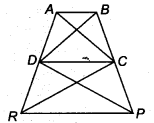

हल:
tfclfiftहमें मिलता है, ar(∆DRC) = ar(∆DPC) [दिया है]
और ये एक ही आधार DC पर हैं।
∴ ∆DRC और ∆DPC समान समांतर रेखाओं के बीच स्थित होने चाहिए।
अतः, DC || RP अर्थात् चतुर्भुज DCPR की सम्मुख भुजाओं का एक युग्म समांतर है।
∴ चतुर्भुज DCPR एक समलम्ब है।
पुनः, हमारे पास है
ar(∆BDP) = ar(∆ARC) [दिया गया है] …(1)
साथ ही, ar(∆DPC) = ar(∆DRC) [दिया गया है] …(2)
(2) को (1) से घटाने पर, हम पाते हैं
ar(∆BDP) – ar(∆DPC) = ar(∆ARQ – ar(∆DRQ
⇒ ar(∆BDC) = ar(∆ADC)
और वे एक ही आधार DC पर हैं।
∴ ABDC और AADC एक ही समानांतर रेखाओं के बीच स्थित होने चाहिए।
इसलिए, AB || DC अर्थात चतुर्भुज ABCD की विपरीत भुजाओं का एक युग्म समानांतर है।
∴ चतुर्भुज ABCD एक समलम्ब चतुर्भुज है।

Ex 9.4

प्रश्न 1.
समांतर चतुर्भुज ABCD और आयत ABEF एक ही आधार AB पर स्थित हैं और उनके क्षेत्रफल बराबर हैं। दर्शाइए कि समांतर चतुर्भुज का परिमाप आयत के परिमाप से बड़ा है।
समाधान:
हमारे पास एक समांतर चतुर्भुज ABCD और आयत ABEF है जिससे
ar(||gm ABCD) = ar( rect. ABEF)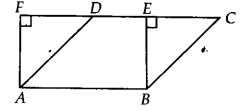

AB = CD [समांतर चतुर्भुज की विपरीत भुजाएँ]
और AB = EF [एक आयत की विपरीत भुजाएँ]
⇒ CD = EF
⇒ AB + CD = AB + EF … (1)
BE < BC और AF < AD [एक समकोण त्रिभुज में, कर्ण सबसे लंबी भुजा होती है] ⇒ (BC + AD) > (BE + AF) …(2)
(1) और (2) से, हमारे पास है
(AB + CD) + (BC+AD) > (AB + EF) + BE + AF)
⇒ (AB + BC + CD + DA) > (AB + BE + EF + FA)
⇒ समांतर चतुर्भुज ABCD का परिमाप > आयत ABEF का परिमाप।

प्रश्न 2.
आकृति में, D और E, BC पर दो बिंदु इस प्रकार हैं कि BD = DE = EC है। दर्शाइए कि ar(ABD) = ar(ADE) = ar(AEC)।

हल:
आइए BC पर लंब AF
इस प्रकार खींचें कि AF, ∆ABD, ∆ADE और ∆AEC की ऊँचाई हो।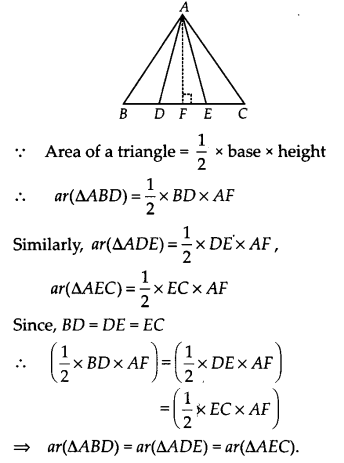

प्रश्न 3.
आकृति में, ABCD, DCFE और ABFE समांतर चतुर्भुज हैं। दर्शाइए कि ar(ADE) = ax(BCF)।

हल:
चूँकि, ABCD एक समांतर चतुर्भुज है [दिया है]
∴ इसकी सम्मुख भुजाएँ समांतर और बराबर हैं।
अर्थात्, AD = BC …(1)
अब, ∆ADE और ∆BCF समान आधारों AD = BC [(1) से] और समान समांतर रेखाओं AB और EF के बीच स्थित हैं।
अतः, ar(∆ADE) = ar(∆BCF)।

प्रश्न 4.
आकृति में, ABCD एक समांतर चतुर्भुज है और BC को एक बिंदु Q तक इस प्रकार बढ़ाया गया है कि AD = CQ है। यदि AQ, DC को P पर प्रतिच्छेद करता है, तो दर्शाइए कि ar(BPC) = ax(DPQ) है। [संकेत: AC को मिलाएँ।]

हल:
हमारे पास एक समांतर चतुर्भुज ABCD है और AD = CQ है। आइए AC को मिलाएँ।
हम जानते हैं कि एक ही आधार पर और एक ही समांतर रेखाओं के बीच स्थित त्रिभुजों का क्षेत्रफल बराबर होता है।
चूँकि, ∆QAC और ∆QDC एक ही आधार QC पर और एक ही समांतर रेखाओं AD और BQ के बीच स्थित हैं।
∴ ar(∆QAC) = ar(∆QDC)
दोनों पक्षों से ar(∆QPC) घटाने पर, हमारे पास है
ar(∆QAQ – ar(∆QPC) = ar(∆QDC) – ar(∆QPC)
⇒ ar(∆PAQ = ar(∆QDP) …(1)
चूँकि, ∆PAC और ∆PBC एक ही आधार PC पर और समान्तर रेखाओं AB और CD के बीच में हैं।
∴ ar(∆PAC) = ar(∆PBC) …(2)
(1) और (2) से, हम पाते हैं
ar(∆PBC) = ar(∆QDP)

प्रश्न 5.
आकृति में, ABC और BDE दो समबाहु त्रिभुज इस प्रकार हैं कि D, BC का मध्य-बिंदु है। यदि AE, BC को F पर प्रतिच्छेद करता है, तो दर्शाइए कि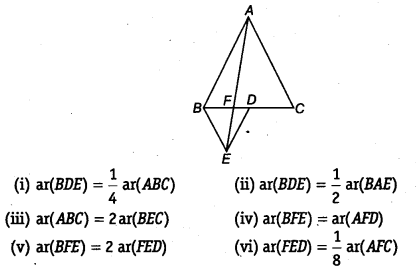

[संकेत: EC और AD को मिलाइए। दर्शाइए कि BE || AC और DE || AB, आदि।]
हल:
आइए EC और AD को मिलाएँ। EP ⊥ BC खींचिए।
मान लीजिए AB = BC = CA = a, तो
BD =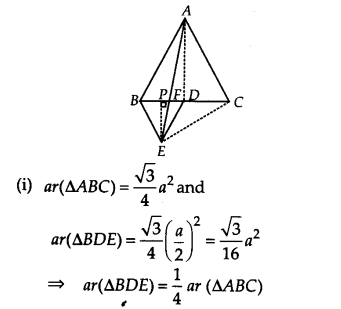a2= DE = BE

(ii) चूँकि, ∆ABC और ∆BED समबाहु त्रिभुज हैं।
⇒ ∠ACB = ∠DBE = 60°
⇒ BE || AC
∆BAE और ∆BEC एक ही आधार BE पर और एक ही समान्तर रेखाओं BE और AC के बीच में हैं।
ar(∆BAE) = ar(∆BEC)
⇒ ar(∆BAE) = 2 ar(∆BDE) [DE, ∆EBC की माध्यिका है। ∴ ar(∆BEC) = || ar(∆BDE)]
⇒ ar(ABDE) =12ar(∆BAE)

(iii) ar(∆ABC) = 4 ar(∆BDE)[(i) भाग में सिद्ध]
ar(∆BEC) = 2 ar(∆BDE)
[ ∵ DE, ∆BEC की माध्यिका है]
⇒ ar(∆ABC) = 2 ar(∆BEC)

(iv) चूँकि, ∆ABC और ∆BDE समबाहु त्रिभुज हैं।
⇒ ∠ABC = ∠BDE = 60°
⇒ AB || DE
∆BED और ∆AED एक ही आधार ED पर और एक ही समान्तर रेखाओं AB और DE के बीच में हैं।
∴ ar(∆BED) = ar(∆AED)
दोनों पक्षों से ar(AEFD) घटाने पर, हम पाते हैं
⇒ ar(∆BED) – ar(∆EFD) = ar(∆AED) – ar(∆EFD)
⇒ ar(∆BEE) = ar(∆AFD)

(v) समकोण ∆ABD में, हम पाते हैं

(1) और (2) से, हम पाते हैं
ar(∆AFD) = 2 ar(∆EFD)
ar(∆AFD) = ar(∆BEF) [(iv) भाग से]
⇒ ar(∆BFE) = 2 ar(∆EFD)

(vi) ar(∆AFC) = ar(∆AFD) + ar(∆ADC)
= ar(∆BFE) +12ar(∆ABC) [(iv) भाग से]
= ar(∆BFE) +12x 4 x ar(∆BDE) [(i) भाग से]
= ar(∆BFE) + 2ar(∆BDE)
= 2ar(∆FED) + 2[ar(∆BFE) + ar(∆FED)]
= 2ar(∆FED) + 2[2ar(∆FED) + ar(∆FED)] [(v से) भाग]
= 2ar(∆FED) + 2[3ar(∆FED)]
= 2ar(∆FED) + 6ar(∆FED)
= 8ar(∆FED)
∴ ar(∆FED) =18ar(∆AFC)

प्रश्न 6.
एक चतुर्भुज ABCD के विकर्ण AC और BD एक दूसरे को P पर प्रतिच्छेद करते हैं। दर्शाइए कि
ar(APB) x ar(CPD) = ar(APD) x ar(BPC)।
[संकेत: A और C से BD पर लंब खींचिए।]
हल:
हमारे पास एक चतुर्भुज ABCD है जिससे इसके विकर्ण AC और BD एक दूसरे को P पर प्रतिच्छेद करते हैं।
आइए AM ⊥ BD और CN ⊥ BD खींचें।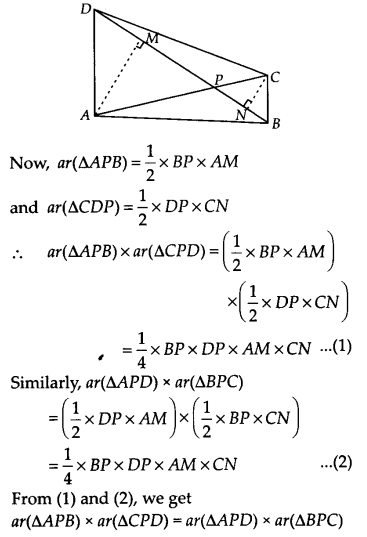

प्रश्न 7.
P और Q क्रमशः एक त्रिभुज ABC की भुजाओं AB और BC के मध्य-बिंदु हैं और R, AP का मध्य-बिंदु है। सिद्ध कीजिए कि

हल:
हमारे पास एक ∆ABC है जिससे P, AB का मध्य-बिंदु है और Q, BC का मध्य-बिंदु है।
साथ ही, R, AP का मध्य-बिंदु है। आइए AQ, RQ, PC और PC को मिलाएँ।

(i) ∆APQ में, R, AP का मध्य-बिंदु है। [दिया है] B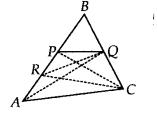

∴RQ, ∆APQ की एक माध्यिका है।
⇒ ar(∆PRQ) =12ar(∆APQ) …(1)
∆ABQ में, P, AB का मध्य-बिंदु है।
∴ QP, ∆ABQ की एक माध्यिका है।
∴ ar(∆APQ) =12ar(∆ABQ) …(2)

प्रश्न 8.
आकृति में, ABC एक समकोण त्रिभुज है जिसका कोण A समकोण है। BCED, ACFG और ABMN क्रमशः भुजाओं BC, CA और AB पर वर्ग हैं। रेखाखंड AX ⊥ DE, BC को Y पर मिलता है। दर्शाइए कि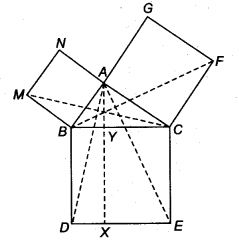

(i) ∆MBC = ∆ABD
(ii) ar(BYXD) = 2 ar(MBC)
(iii) ar(BYXD) = ax(ABMN)
(iv) ∆FCB ≅ ∆ACE
(v) ar(CYXE) = 2 ar(FCB)
(vi) ar(CYXE) = ax(ACFG)
(vii) ar(BCED) = ar(ABMN) + ar(ACFG)
हल:
हमारे पास एक समकोण ∆ABC है जिससे BCED, ACFG और ABMN क्रमशः इसकी भुजाओं BC, CA और AB पर वर्ग हैं। रेखाखंड AX 1 DE भी इस प्रकार खींचा गया है कि वह BC से Y पर मिलता है।

(i) ∠CBD = ∠MBA [प्रत्येक 90°]
∴ ∠CBD + ∠ABC = ∠MBA + ∠ABC
(दोनों तरफ ∠ABC जोड़ने पर)
या ∠ABD = ∠MBC
∆ABD और ∆MBC में, हमारे पास है
AB = MB [एक वर्ग की भुजाएँ]
BD = BC
∠ABD = ∠MBC [ऊपर सिद्ध]
∴ ∆ABD = ∆MBC [SAS सर्वांगसमता द्वारा]

(ii) चूँकि समांतर चतुर्भुज BYXD और ∆ABD एक ही आधार BD पर तथा एक ही समांतर रेखाओं BD और AX के बीच स्थित हैं।
∴ ar(∆ABD) =12ar(|| gm BYXD)
लेकिन ∆ABD ≅ ∆MBC [(i) भाग से]
चूँकि, सर्वांगसम त्रिभुजों के
क्षेत्रफल समान होते हैं।
∴ ar(∆MBC) =12ar(|| gm BYXD)
⇒ ar(|| gm BYXD) = 2ar(∆MBC)

(iii) चूंकि, ar(|| gm BYXD) = 2ar(∆MBC) …(1) [(ii) भाग से]
और or(वर्ग ABMN) = 2or(∆MBC) …(2)
[ABMN और AMBC एक ही आधार MB पर और एक ही समान्तर रेखाओं MB और NC के बीच हैं]
(1) और (2) से, हमारे पास
ar(BYXD) = ar(ABMN) है।

(iv) ∠FCA = ∠BCE (प्रत्येक 90°)
या ∠FCA+ ∠ACB = ∠BCE+ ∠ACB
[दोनों तरफ ∠ACB जोड़ने पर]
⇒ ∠FCB = ∠ACE
∆FCB और ∆ACE में, हमारे पास है
FC = AC [वर्ग की भुजाएँ]
CB = CE [वर्ग की भुजाएँ]
∠FCB = ∠ACE [ऊपर सिद्ध]
⇒ ∆FCB ≅ ∆ACE [SAS सर्वांगसमता द्वारा]

(v) चूँकि, || gm CYXE और ∆ACE एक ही आधार CE पर और समान्तर रेखाओं CE और AX के बीच स्थित हैं।
∴ ar(|| gm CYXE) = 2ar(∆ACE)
लेकिन ∆ACE ≅ ∆FCB [(iv) भाग से]
चूँकि, सर्वांगसम त्रिभुज क्षेत्रफलों में बराबर होते हैं।
∴ ar (||< gm CYXE) = 2ar(∆FCB)

(vi) चूँकि, ar(|| gm CYXE) = 2ar(∆FCB) …(3)
[(v) भाग से]
साथ ही (quad. ACFG) और ∆FCB एक ही आधार FC पर और एक ही समान्तर रेखाओं FC और BG के बीच में हैं।
⇒ ar(quad. ACFG) = 2ar(∆FCB) …(4)
(3) और (4) से, हम पाते हैं
ar(quad. CYXE) = ar(quad. ACFG) …(5)

(vii) हमारे पास है ar(quad. BCED)
= ar(quad. CYXE) + ar(quad. BYXD)
= ar(quad. CYXE) + ar(quad. ABMN)
[(iii) भाग से]
इस प्रकार, ar (quad. BCED)
= ar(quad. ABMN) + ar(quad. ACFG)
[(vi) भाग से]