SikhLo - Current Affairs in Hindi, Daily current affairs, Current affairs

 NCERT Class 9 Maths Chapter 8 चतुर्भुज

NCERT Solutions for Class 9 Maths Chapter 8 चतुर्भुज

Ex 8.1

प्रश्न 1.
चतुर्भुज के कोण 3 : 5 : 9 : 13 के अनुपात में हैं। चतुर्भुज के सभी कोण ज्ञात कीजिए।
हल:
माना चतुर्भुज के कोण 3x, 5x, 9x और 13x हैं।
∴ 3x + 5x + 9x + 13x = 360°
[चतुर्भुज का कोण योग गुण]
⇒ 30x = 360°
⇒ x = \(\frac { { 360 }^{ \circ } }{ 30 } \) = 12°360∘30= 12°
∴ 3x = 3 x 12° = 36°
5x = 5 x 12° = 60°
9x = 9 x 12° = 108°
13a = 13 x 12° = 156°
⇒ चतुर्भुज के आवश्यक कोण 36°, 60°, 108° और 156° हैं।

प्रश्न 2.
यदि एक समांतर चतुर्भुज के विकर्ण बराबर हैं, तो दर्शाइए कि यह एक आयत है।
हल:
मान लीजिए ABCD एक समांतर चतुर्भुज है जिससे AC = BD है।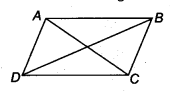

∆ABC और ∆DCB में,
AC = DB [दिया है]
AB = DC [समांतर चतुर्भुज की सम्मुख भुजाएँ]
BC = CB [उभयनिष्ठ]
∴ ∆ABC ≅ ∆DCB [SSS सर्वांगसमता से]
⇒ ∠ABC = ∠DCB [CPCT से] …(1)
अब, AB || DC और BC एक तिर्यक रेखा है। [∵ ABCD एक समांतर चतुर्भुज है]
∴ ∠ABC + ∠DCB = 180° … (2) [सह-अंतर कोण]
(1) और (2) से, हमें प्राप्त है
∠ABC = ∠DCB = 90°
अर्थात, ABCD एक समांतर चतुर्भुज है जिसका कोण 90° के बराबर है।
∴ ABCD एक आयत है।

प्रश्न 3.
दर्शाइए कि यदि किसी चतुर्भुज के विकर्ण परस्पर समकोण पर समद्विभाजित करते हैं, तो वह एक समचतुर्भुज होता है।
हल:
मान लीजिए ABCD एक चतुर्भुज है जिससे विकर्ण AC और BD एक दूसरे को O पर समकोण पर समद्विभाजित करते हैं।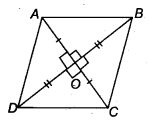

∴ ∆AOB और ∆AOD में, हमारे पास
AO = AO [उभयनिष्ठ]
OB = OD [O, BD का मध्य-बिंदु है]
∠AOB = ∠AOD [प्रत्येक 90°]
∴ ∆AQB ≅ ∆AOD [SAS सर्वांगसमता से
∴ AB = AD [CPCT से] ……..(1)
इसी प्रकार, AB = BC .. .(2)
BC = CD …..(3)
CD = DA ……(4)
∴ (1), (2), (3) और (4) से, हमारे पास
AB = BC = CD = DA
है
वैकल्पिक रूप से: ABCD को पहले एक समांतर चतुर्भुज सिद्ध किया जा सकता है, फिर आसन्न भुजाओं के एक युग्म को बराबर सिद्ध करने पर समचतुर्भुज प्राप्त होगा।

प्रश्न 4.
दर्शाइए कि एक वर्ग के विकर्ण बराबर होते हैं और एक दूसरे को समकोण पर समद्विभाजित करते हैं।
हल:
मान लीजिए ABCD एक वर्ग है जिसके विकर्ण AC और BD एक दूसरे को बिंदु O पर प्रतिच्छेद करते हैं।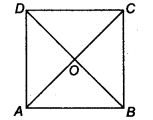

(i) विकर्णों को बराबर सिद्ध करने के लिए, हमें AC = BD सिद्ध करना होगा।
∆ABC और ∆BAD में,
AB = BA [उभयनिष्ठ]
BC = AD [वर्ग ABCD की भुजाएँ]
∠ABC = ∠BAD [प्रत्येक कोण 90° का है]
∴ ∆ABC ≅ ∆BAD [SAS सर्वांगसमता से]
AC = BD [CPCT से] …(1)

(ii) AD || BC और AC एक तिर्यक रेखा है। [∵ एक वर्ग एक समांतर चतुर्भुज है]
∴ ∠1 = ∠3
[एकांतर आंतरिक कोण बराबर हैं]
इसी तरह, ∠2 = ∠4
अब, ∆OAD और ∆OCB में, हमारे पास है
AD = CB [एक वर्ग ABCD की भुजाएँ]
∠1 = ∠3 [सिद्ध]
∠2 = ∠4 [सिद्ध]
∴ ∆OAD ≅ ∆OCB [ASA सर्वांगसमता से]
⇒ OA = OC और OD = OB [CPCT से]
यानी, विकर्ण AC और BD एक दूसरे को O पर समद्विभाजित करते हैं। …….(2)

(iii) ∆OBA और ∆ODA में, हमारे पास है
OB = OD [सिद्ध]
BA = DA [वर्ग ABCD की भुजाएँ]
OA = OA [उभयनिष्ठ]
∴ ∆OBA ≅ ∆ODA [SSS सर्वांगसमता से]
⇒ ∠AOB = ∠AOD [CPCT से] …(3)
∵ ∠AOB और ∠AOD एक रैखिक युग्म बनाते हैं।
∴∠AOB + ∠AOD = 180°
∴∠AOB = ∠AOD = 90° [(3) से]
⇒ AC ⊥ BD …(4)
(1), (2) और (4) से, हम पाते हैं कि AC और BD बराबर हैं और एक दूसरे को समकोण पर समद्विभाजित करते हैं।

प्रश्न 5.
दर्शाइए कि यदि किसी चतुर्भुज के विकर्ण बराबर हों और एक दूसरे को समकोण पर समद्विभाजित करते हों, तो वह एक वर्ग होता है।
हल:
मान लीजिए ABCD एक चतुर्भुज है जिसके विकर्ण AC और BD बराबर हैं और एक दूसरे को समकोण पर समद्विभाजित करते हैं।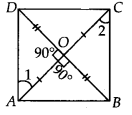

अब, ∆AOD और ∆AOB में, हमारे पास है
∠AOD = ∠AOB [प्रत्येक 90°]
AO = AO [उभयनिष्ठ]
OD = OB [ ∵ O, BD का मध्यबिंदु है]
∴ ∆AOD ≅ ∆AOB [SAS सर्वांगसमता से]
⇒ AD = AB [CPCT से] …(1)
इसी प्रकार, हमारे पास है
AB = BC … (2)
BC = CD …(3)
CD = DA …(4)
(1), (2), (3) और (4) से, हमारे पास है
AB = BC = CD = DA
∴ चतुर्भुज ABCD की सभी भुजाएँ बराबर हैं।
∆AOD और ∆COB में, हमारे पास है
AO = CO [दिया गया है]
OD = OB [दिया गया है]
∠AOD = ∠COB [ऊर्ध्वाधर रूप से विपरीत कोण]
तो, ∆AOD ≅ ∆COB [SAS सर्वांगसमता से]
∴∠1 = ∠2 [CPCT से]
लेकिन, वे एकांतर आंतरिक कोणों की एक जोड़ी बनाते हैं।
∴ AD || BC
इसी प्रकार, AB || DC
∴ ABCD एक समांतर चतुर्भुज है।
∴ समांतर चतुर्भुज जिसकी सभी भुजाएँ बराबर हों, एक समचतुर्भुज होता है।
∴ ABCD एक समचतुर्भुज है।
अब, ∆ABC और ∆BAD में,
AC = BD [दिया है]
BC = AD [सिद्ध]
AB = BA [उभयनिष्ठ]
∴ ∆ABC ≅ ∆BAD [SSS सर्वांगसमता से]
∴ ∠ABC = ∠BAD [CPCT से] ……(5)
चूँकि, AD || BC और AB एक तिर्यक रेखा है।
∴∠ABC + ∠BAD = 180° .. .(6) [ सह – आंतरिक कोण]
⇒ ∠ABC = ∠BAD = 90° [(5) और (6) से]
अतः, समचतुर्भुज ABCD का एक कोण 90° के बराबर है।
इस प्रकार, ABCD एक वर्ग है।

प्रश्न 6.
एक समांतर चतुर्भुज ABCD का विकर्ण AC, ∠A को समद्विभाजित करता है (चित्र देखें)। दर्शाइए कि
(i) यह ∠C को भी समद्विभाजित करता है,
(ii) ABCD एक समचतुर्भुज है।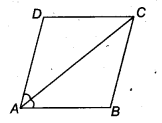

हल:
हमारे पास एक समांतर चतुर्भुज ABCD है जिसमें विकर्ण AC, ∠A को समद्विभाजित करता है
⇒ ∠DAC = ∠BAC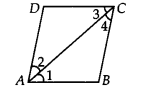

(i) चूँकि, ABCD एक समांतर चतुर्भुज है।
∴ AB || DC और AC एक तिर्यक रेखा है।
∴ ∠1 = ∠3 …(1)
[ ∵ एकांतर अंतः कोण बराबर हैं]
साथ ही, BC || AD और AC एक तिर्यक रेखा है।
∴ ∠2 = ∠4 …(2)
[ v वैकल्पिक आंतरिक कोण बराबर हैं]
साथ ही, ∠1 = ∠2 …(3)
[ ∵ AC, ∠A को समद्विभाजित करता है]
(1), (2) और (3) से, हमें प्राप्त है
∠3 = ∠4
⇒ AC, ∠C को समद्विभाजित करता है।

(ii) ∆ABC में,
∠1 = ∠4 [(2) और (3) से]
⇒ BC = AB …(4)
[ ∵ ∆ के बराबर कोणों के सम्मुख भुजाएँ बराबर होती हैं]
इसी प्रकार, AD = DC ……..(5)
लेकिन, ABCD एक समांतर चतुर्भुज है। [दिया है]
∴ AB = DC …(6)
(4), (5) और (6) से,
AB = BC = CD = DA
इस प्रकार, ABCD एक समचतुर्भुज है।

प्रश्न 7.
ABCD एक समचतुर्भुज है। दर्शाइए कि विकर्ण AC, ∠A के साथ-साथ ∠C को भी समद्विभाजित करता है और विकर्ण BD, ∠B के साथ-साथ ∠D को भी समद्विभाजित करता है।
हल:
चूँकि, ABCD एक समचतुर्भुज है।
⇒ AB = BC = CD = DA
साथ ही, AB || CD और AD || BC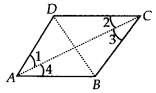

अब, CD = AD ⇒ ∠1 = ∠2 …….(1)
[ ∵ त्रिभुज की बराबर भुजाओं के सम्मुख कोण बराबर होते हैं]
साथ ही, AD || BC और AC एक तिर्यक रेखा है।
[ ∵ प्रत्येक समचतुर्भुज एक समांतर चतुर्भुज होता है]
⇒ ∠1 = ∠3 …(2)
[ ∵ एकांतर अंतः कोण बराबर होते हैं]
(1) और (2) से, हमें
∠2 = ∠3 …(3) मिलता है
क्योंकि, AB || DC और AC एक तिर्यक रेखा है।
∴ ∠2 = ∠4 …(4)
[ ∵ एकांतर अंतः कोण बराबर होते हैं] (1) और (4) से,
हमें प्राप्त है ∠1 = ∠4
∴ AC, ∠C के साथ-साथ ∠A को भी समद्विभाजित करता है।
इसी प्रकार, हम सिद्ध कर सकते हैं कि BD, ∠B के साथ-साथ ∠D को भी समद्विभाजित करता है।

प्रश्न 8.
ABCD एक आयत है जिसमें विकर्ण AC, ∠A और ∠C दोनों को समद्विभाजित करता है। दर्शाइए कि
(i) ABCD एक वर्ग है
(ii) विकर्ण BD, ∠B और ∠D दोनों को समद्विभाजित करता है।
हल:
हमारे पास एक आयत ABCD है जिससे AC, ∠A और ∠C दोनों को समद्विभाजित करता है।
अर्थात्, ∠1 = ∠4 और ∠2 = ∠3 ……..(1)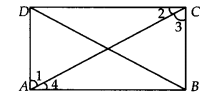

(i) चूंकि, प्रत्येक आयत एक समांतर चतुर्भुज है।
∴ ABCD एक समांतर चतुर्भुज है।
⇒ AB || CD और AC एक तिर्यक रेखा है।
∴∠2 = ∠4 …(2)
[ ∵ एकांतर अंतः कोण बराबर हैं]
(1) और (2) से, हमारे पास है
∠3 = ∠4
∆ABC में, ∠3 = ∠4
⇒ AB = BC
[ ∵ एक A के बराबर कोणों के विपरीत भुजाएँ बराबर होती हैं]
इसी प्रकार, CD = DA
इसलिए, ABCD एक आयत है जिसमें आसन्न भुजाएँ बराबर हैं।
⇒ ABCD एक वर्ग है।

(ii) चूँकि ABCD एक वर्ग है और वर्ग के विकर्ण सम्मुख कोणों को समद्विभाजित करते हैं।
अतः BD, ∠B के साथ-साथ ∠D को भी समद्विभाजित करता है।

प्रश्न 9.
समांतर चतुर्भुज ABCD में, विकर्ण BD पर दो बिंदु P और Q इस प्रकार लिए गए हैं कि DP = BQ (देखिए आकृति)। दर्शाइए कि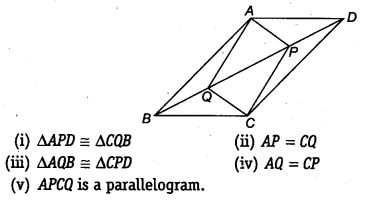

हल:
हमारे पास एक समांतर चतुर्भुज ABCD है, BD विकर्ण है और बिंदु P और Q इस प्रकार हैं कि PD = QB

(i) चूँकि AD || BC और BD एक तिर्यक रेखा है।
∴ ∠ADB = ∠CBD [ ∵ एकांतर अंतः कोण बराबर हैं]
⇒ ∠ADP = ∠CBQ
अब, ∆APD और ∆CQB में,
AD = CB [समानांतर चतुर्भुज ABCD की सम्मुख भुजाएँ बराबर हैं]
PD = QB [दिया है]
∠ADP = ∠CBQ [सिद्ध]
∴ ∆APD ≅ ∆CQB [SAS सर्वांगसमता से]

(ii) चूँकि, ∆APD ≅ ∆CQB [सिद्ध]
⇒ AP = CQ [CPCT द्वारा]

(iii) चूँकि AB || CD और BD एक तिर्यक रेखा है।
∴ ∠ABD = ∠CDB
⇒ ∠ABQ = ∠CDP
अब, ∆AQB और ∆CPD में,
QB = PD [दिया है]
∠ABQ = ∠CDP [सिद्ध]
AB = CD [Y एक समांतर चतुर्भुज ABCD की सम्मुख भुजाएँ बराबर होती हैं]
∴ ∆AQB = ∆CPD [SAS सर्वांगसमता से]

(iv) चूँकि, ∆AQB = ∆CPD [सिद्ध]
⇒ AQ = CP [CPCT से]

(v) चतुर्भुज ∆PCQ में,
सम्मुख भुजाएँ बराबर होती हैं। [सिद्ध]
∴ ∆PCQ एक समांतर चतुर्भुज है।

प्रश्न 10.
ABCD एक समांतर चतुर्भुज है और AP तथा CQ शीर्षों A और C से विकर्ण BD पर लंब हैं (देखिए आकृति)। दर्शाइए कि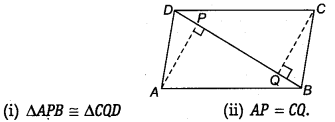

हल:
(i) ∆APB और ∆CQD में,
∠APB = ∠CQD [प्रत्येक 90°]
AB = CD [∵ समांतर चतुर्भुज ABCD की सम्मुख भुजाएँ बराबर होती हैं]
∠ABP = ∠CDQ
[∵ एकांतर कोण बराबर होते हैं क्योंकि AB || CD और BD एक तिर्यक रेखा है]
∴ ∆APB = ∆CQD [AAS सर्वांगसमता से]

(ii) चूँकि, ∆APB ≅ ∆CQD [सिद्ध]
⇒ AP = CQ [CPCT द्वारा]

प्रश्न 11.
∆ABC और ∆DEF में, AB = DE, AB || DE, BC – EF और BC || EF है। शीर्ष A, B और C क्रमशः शीर्ष D, E और F से जुड़े हुए हैं (आकृति देखें)।
दर्शाइए कि
(i) चतुर्भुज ABED एक समांतर चतुर्भुज है
(ii) चतुर्भुज BEFC एक समांतर चतुर्भुज है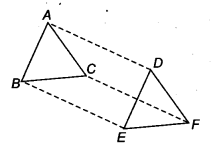

(iii) AD || CF और AD = CF
(iv) चतुर्भुज ACFD एक समांतर चतुर्भुज है
(v) AC = DF
(vi) ∆ABC ≅ ∆DEF
हल:
(i) हमें मिलता है AB = DE [दिया है]
और AB || DE [दिया है]
अर्थात्, ABED एक चतुर्भुज है जिसमें विपरीत भुजाओं (AB और DE) का एक युग्म समांतर और समान लंबाई का है।
∴ ABED एक समांतर चतुर्भुज है।

(ii) BC = EF [दिया है]
तथा BC || EF [दिया है]
अर्थात् BEFC एक चतुर्भुज है जिसमें सम्मुख भुजाओं का एक युग्म (BC तथा EF) समान्तर तथा समान लम्बाई का है।
∴ BEFC एक समांतर चतुर्भुज है।

(iii) ABED एक समांतर चतुर्भुज है [सिद्ध]
∴ AD || BE और AD = BE …(1)
[ ∵ समांतर चतुर्भुज की सम्मुख भुजाएँ बराबर और समांतर होती हैं] साथ ही, BEFC एक समांतर चतुर्भुज है। [सिद्ध]
BE || CF और BE = CF …(2)
[ ∵ समांतर चतुर्भुज की सम्मुख भुजाएँ बराबर और समांतर होती हैं]
(1) और (2) से, हमें
AD || CF और AD = CF प्राप्त होता है।

(iv) चूँकि, AD || CF तथा AD = CF [सिद्ध]
अर्थात्, चतुर्भुज ACFD में, सम्मुख भुजाओं का एक युग्म (AD तथा CF) समान्तर तथा समान लम्बाई का है।
∴चतुर्भुज ACFD एक समांतर चतुर्भुज है।

(v) चूँकि, ACFD एक समांतर चतुर्भुज है। [सिद्ध]
अतः, AC = DF [∵ समांतर चतुर्भुज की सम्मुख भुजाएँ बराबर होती हैं]

(vi) ∆ABC और ∆DFF में,
AB = DE [दिया गया है]
BC = EF [दिया गया है]
AC = DE [(v) भाग में सिद्ध]
∆ABC ≅ ∆DFF [SSS सर्वांगसमता द्वारा]

प्रश्न 12.
ABCD एक समलम्ब चतुर्भुज है जिसमें AB || CD और AD = BC है (आकृति देखें)। दर्शाइए कि
(i)∠A=∠B
(ii)∠C=∠D
(iii) ∆ABC ≅ ∆BAD
(iv) विकर्ण AC = विकर्ण BD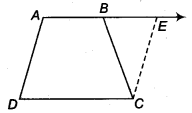

[संकेत: AB को बढ़ाइए और C से DA के समांतर एक रेखा खींचिए जो बढ़ाई गई AB को E पर प्रतिच्छेद करे]।
हल:
हमें एक समलम्ब चतुर्भुज ABCD दिया गया है जिसमें AB || CD और AD = BC है।

(i) AB को E तक बढ़ाइए और CF || AD खींचिए। (1)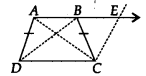

∵ AB || DC
⇒ AE || DC साथ ही AD || CF
∴ AECD एक समान्तर चतुर्भुज है।
⇒ AD = CE …(1)
[ ∵ समांतर चतुर्भुज की सम्मुख भुजाएँ बराबर होती हैं]
लेकिन AD = BC …(2) [दिया गया है]
(1) और (2) से, BC = CF
अब, ∆BCF में, BC = CF है
⇒ ∠CEB = ∠CBE …(3)
[ ∵ त्रिभुज की बराबर भुजाओं के सम्मुख कोण बराबर होते हैं]
साथ ही, ∠ABC + ∠CBE = 180° … (4)
[रैखिक युग्म]
और ∠A + ∠CEB = 180° …(5)
[समांतर चतुर्भुज ADCE के सह-अंतर्कोण]
(4) और (5) से, हम पाते हैं
∠ABC + ∠CBE = ∠A + ∠CEB
⇒ ∠ABC = ∠A [(3) से]
⇒ ∠B = ∠A …(6)

(ii) AB || CD और AD एक तिर्यक रेखा है।
∴ ∠A + ∠D = 180° …(7) [सह-अंतर कोण]
इसी प्रकार, ∠B + ∠C = 180° … (8)
(7) और (8) से, हम पाते हैं
∠A + ∠D = ∠B + ∠C
⇒ ∠C = ∠D [(6) से]

(iii) ∆ABC और ∆BAD में,
AB = BA [उभयनिष्ठ]
BC = AD [दिया है]
∠ABC = ∠BAD [सिद्ध]
∴ ∆ABC = ∆BAD [SAS सर्वांगसमता द्वारा]

(iv) चूँकि, ∆ABC = ∆BAD [सिद्ध]
⇒ AC = BD [CPCT द्वारा]

Ex 8.2

प्रश्न 1.
ABCD एक चतुर्भुज है जिसमें P, Q, R और S भुजाओं AB, BC, CD और DA के मध्य-बिंदु हैं (चित्र देखें)। AC एक विकर्ण है। दर्शाइए कि
(i) SR || AC और SR =12AC
(ii) PQ = SR
(iii) PQRS एक समांतर चतुर्भुज है।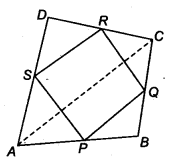

हल:
(i) ∆ACD में,
∴ S, AD का मध्य-बिंदु है और R, CD का मध्य-बिंदु है।
SR =12AC और SR || AC …(1)
[मध्य-बिंदु प्रमेय द्वारा]

(ii) ∆ABC में, P, AB का मध्य-बिंदु है और Q, BC का मध्य-बिंदु है।
PQ =12AC और PQ || AC …(2)
[मध्य-बिंदु प्रमेय द्वारा]
(1) और (2) से, हम पाते हैं
PQ =12AC = SR और PQ || AC || SR
⇒ PQ = SR और PQ || SR
(iii) चतुर्भुज PQRS में,
PQ = SR और PQ || SR [सिद्ध]
∴ PQRS एक समांतर चतुर्भुज है।

प्रश्न 2.
ABCD एक समचतुर्भुज है और P, Q, R और S क्रमशः भुजाओं AB, BC, CD और DA के मध्य-बिंदु हैं। दर्शाइए कि चतुर्भुज PQRS एक आयत है।
हल:
हमारे पास एक समचतुर्भुज ABCD है और P, Q, R और S क्रमशः भुजाओं AB, BC, CD और DA के मध्य-बिंदु हैं। AC को मिलाइए।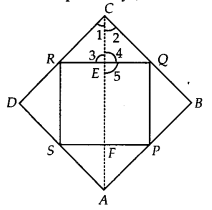

∆ABC में, P और Q क्रमशः AB और BC के मध्य-बिंदु हैं।
∴ PQ =12AC और PQ || AC …(1)
[मध्य-बिंदु प्रमेय से]
∆ADC में, R और S क्रमशः CD और DA के मध्य-बिंदु हैं।
∴ SR =12AC और SR || AC …(2)
[मध्य-बिंदु प्रमेय द्वारा]
(1) और (2) से, हम पाते हैं
PQ =12AC = SR और PQ || AC || SR
⇒ PQ = SR और PQ || SR
∴ PQRS एक समांतर चतुर्भुज है। …….(3)
अब, ∆ERC और ∆EQC में,
∠1 = ∠2
[ ∵ एक समचतुर्भुज के विकर्ण विपरीत कोणों को समद्विभाजित करते हैं]
CR = CQ [ ∵सीडी2=बी सी2]
CE = CE [उभयनिष्ठ]
∴ ∆ERC ≅ ∆EQC [SAS सर्वांगसमता से]
⇒ ∠3 = ∠4 …(4) [CPCT से]
लेकिन ∠3 + ∠4 = 180° ……(5) [रैखिक युग्म]
(4) और (5) से, हम पाते हैं
⇒ ∠3 = ∠4 = 90°
अब, ∠RQP = 180° – ∠b [ Y PQ के लिए सह-आंतरिक कोण || AC और EQ तिर्यक रेखा है]
लेकिन ∠5 = ∠3
[∵ शीर्षाभिमुख कोण बराबर होते हैं]
∴ ∠5 = 90°
इसलिए, ∠RQP = 180° – ∠5 = 90°
∴ समांतर चतुर्भुज PQRS का एक कोण 90° है।
इस प्रकार, PQRS एक आयत है।

प्रश्न 3.
ABCD एक आयत है और P, Q, R और S क्रमशः भुजाओं AB, BC, CD और DA के मध्य-बिंदु हैं। दर्शाइए कि चतुर्भुज PQRS एक समचतुर्भुज है।
हल: अब,
∆ABC में,
PQ =12AC और PQ || AC …(1)
[मध्य-बिंदु प्रमेय द्वारा]
इसी प्रकार, ∆ADC में,
SR =12AC और SR || AC …(2)
(1) और (2) से, हम पाते हैं कि
PQ = SR और PQ || SR
∴ PQRS एक समांतर चतुर्भुज है।
अब, ∆PAS और ∆PBQ में, हमारे पास है
∠A = ∠B [प्रत्येक 90°]
AP = BP [ ∵ P, AB का मध्य-बिंदु है]
AS = BQ [ ∵12AD =12BC]
∴ ∆PAS ≅ ∆PBQ [SAS सर्वांगसमता से]
⇒ PS = PQ [CPCT से]
साथ ही, PS = QR और PQ = SR [∵एक समांतर चतुर्भुज की सम्मुख भुजाएँ बराबर होती हैं]
अतः, PQ = QR = RS = SP अर्थात्, PQRS एक समांतर चतुर्भुज है जिसकी सभी भुजाएँ बराबर हैं।
अतः, PQRS एक समचतुर्भुज है।

प्रश्न 4.
ABCD एक समलम्ब चतुर्भुज है जिसमें AB || DC, BD एक विकर्ण है और E, AD का मध्य-बिंदु है। E से AB के समांतर एक रेखा खींची गई है जो BC को F पर काटती है (चित्र देखें)। दर्शाइए कि F, BC का मध्य-बिंदु है।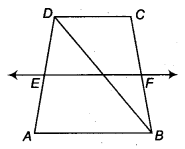

हल: ∆DAB में,
हम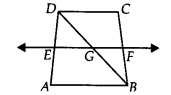

जानते हैं कि E, AD का मध्य-बिंदु है
और EG || AB [∵ EF || AB]
मध्य-बिंदु प्रमेय के विलोम का उपयोग करने पर, हम पाते हैं, G, BD का मध्य-बिंदु है।
पुनः ABDC में, G, BD का मध्य-बिंदु है और GF || DC है।
[∵ AB || DC और EF || AB और GF, EF का एक भाग है]
मध्य-बिंदु प्रमेय के विलोम का उपयोग करने पर, हम पाते हैं, F, BC का मध्य-बिंदु है।

प्रश्न 5.
एक समांतर चतुर्भुज ABCD में, E और F क्रमशः भुजाओं AB और CD के मध्य-बिंदु हैं (चित्र देखें)। दर्शाइए कि रेखाखंड AF और EC विकर्ण BD को समद्विभाजित करते हैं।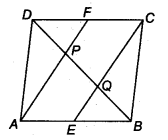

हल:
चूँकि, समांतर चतुर्भुज की सम्मुख भुजाएँ समांतर और बराबर होती हैं।
∴ AB || DC
⇒ AE || FC …(1)
और AB = DC
⇒12AB =12DC
⇒ AE = FC …(2)
(1) और (2) से, हमें
AE || PC और AE = PC मिलता है
∴ ∆ECF एक समांतर चतुर्भुज है।
अब, ∆DQC में, F, DC का मध्य-बिंदु है और FP || CQ है
[∵ AF || CE]
⇒ DP = PQ …(3)
[मध्य-बिंदु प्रमेय के विलोम से] इसी प्रकार, A BAP में, E, AB का मध्य-बिंदु है और EQ || AP है [∵AF || CE]
⇒ BQ = PQ …(4)
[मध्य-बिंदु प्रमेय के विलोम से]
∴ (3) और (4) से, हमें
DP = PQ = BQ मिलता है
इसलिए, रेखाखंड AF और EC विकर्ण BD को समद्विभाजित करते हैं।

प्रश्न 6.
दर्शाइए कि एक चतुर्भुज की सम्मुख भुजाओं के मध्य-बिंदुओं को मिलाने वाले रेखाखंड एक-दूसरे को समद्विभाजित करते हैं।
हल:
मान लीजिए ABCD एक चतुर्भुज है, जहाँ P, Q, R और S क्रमशः भुजाओं AB, BC, CD और DA के मध्य-बिंदु हैं।
PQ, QR, RS और SP को मिलाएँ।
आइए PR, SQ और AC को भी मिलाएँ।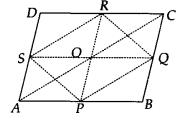

अब, ∆ABC में, P और Q क्रमशः इसकी भुजाओं AB और BC के मध्य-बिंदु हैं।
∴ PQ || AC और PQ =12AC …(1)
[मध्य-बिंदु प्रमेय द्वारा]
इसी प्रकार, RS || AC और RS =12AC …(2)
∴ (1) और (2) से, हम पाते हैं कि
PQ || RS, PQ = RS
∴ PQRS एक समांतर चतुर्भुज है।
और समांतर चतुर्भुज के विकर्ण एक दूसरे को समद्विभाजित करते हैं, अर्थात PR और SQ एक दूसरे को समद्विभाजित करते हैं। इस प्रकार, चतुर्भुज ABCD की सम्मुख भुजाओं के मध्य-बिंदुओं को मिलाने वाले रेखाखंड एक दूसरे को समद्विभाजित करते हैं।

प्रश्न 7.
ABC एक त्रिभुज है जिसका कोण C समकोण है। कर्ण AB के मध्य-बिंदु M से होकर BC के समांतर एक रेखा AC को D पर प्रतिच्छेद करती है। दर्शाइए कि
(i) D, AC का मध्य-बिंदु है।
(ii) MD ⊥ AC
हल:
हमारे पास है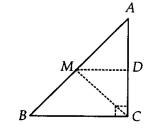

(i) ∆ACB में,
M, AB का मध्य-बिंदु है। [दिया है]
MD || BC, [दिया है]
∴ मध्य-बिंदु प्रमेय के विलोम का उपयोग करते हुए,
D, AC का मध्य-बिंदु है।

(ii) चूँकि, MD || BC और AC एक तिर्यक रेखा है।
∠MDA = ∠BCA
[ ∵ संगत कोण बराबर हैं] क्योंकि
∠BCA = 90° [दिया है]
∠MDA = 90°
⇒ MD ⊥AC.