NCERT Class 9 Maths Chapter 7 त्रिभुज
NCERT Solutions for Class 9 Maths Chapter 7 त्रिभुज
Ex 7.1
प्रश्न 1.
चतुर्भुज ACBD में, AC = AD और AB, ∠A को समद्विभाजित करता है (चित्र देखें)। दर्शाइए कि ∆ABC ≅ ∆ABD। आप BC और BD के बारे में क्या कह सकते हैं?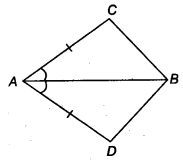
हल:
चतुर्भुज ACBD में, AC = AD और AB, ∠A का समद्विभाजक है।
अब, ∆ABC और ∆ABD में,
AC = AD (दिया है)
∠ CAB = ∠ DAB (AB, ∠ CAB को समद्विभाजित करता है)
और AB = AB (उभयनिष्ठ)
∴ ∆ ABC ≅ ∆ABD (SAS सर्वांगसमता अभिगृहीत से)
∴ BC = BD (CPCT से)
प्रश्न 2.
ABCD एक चतुर्भुज है जिसमें AD = BC और ∠ DAB = ∠ CBA है (आकृति देखें)। सिद्ध कीजिए कि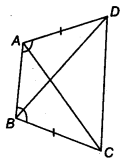
(i) ∆ABD ≅ ∆BAC
(ii) BD = AC
(iii) ∠ABD = ∠ BAC
हल:
चतुर्भुज ACBD में, AD = BC और ∠ DAB = ∠ CBA है।
(i) ∆ ABC और ∆ BAC में,
AD = BC (दिया गया है)
∠DAB = ∠CBA (दिया गया है)
AB = AB (उभयनिष्ठ)
∴ ∆ ABD ≅ ∆BAC (SAS सर्वांगसमता से)
(ii) चूँकि ∆ABD ≅ ∆BAC
⇒ BD = AC [CPCT से]
(iii) चूँकि ∆ABD ≅ ∆BAC
⇒ ∠ABD = ∠BAC [CPCT से]
प्रश्न 3.
AD और BC एक रेखाखंड AB पर समान लंब हैं (चित्र देखें)। दर्शाइए कि CD, AB को समद्विभाजित करती है।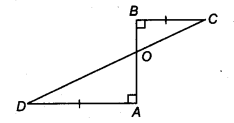
हल:
∆BOC और ∆AOD में,
∠BOC = ∠AOD
BC = AD [दिया है]
∠BOC = ∠AOD [शीर्षाभिमुख कोण]
∴ ∆OBC ≅ ∆OAD [AAS सर्वांगसमता से]
⇒ OB = OA [CPCT से]
अर्थात्, O, AB का मध्य-बिंदु है।
अतः CD, AB को समद्विभाजित करती है।
प्रश्न 4.
l और m दो समांतर रेखाएँ हैं जो समांतर रेखाओं p और q के एक अन्य युग्म द्वारा प्रतिच्छेदित होती हैं (चित्र देखें)। दर्शाइए कि ∆ABC = ∆CDA।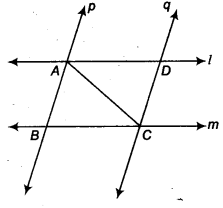
हल:
∵ p || q और AC एक तिर्यक रेखा है,
∴ ∠BAC = ∠DCA …(1) [एकांतर अंतः कोण]
इसी प्रकार l || m और AC एक तिर्यक रेखा है,
∴ ∠BCA = ∠DAC …(2)
[एकांतर अंतः कोण]
अब, ∆ABC और ∆CDA में,
∠BAC = ∠DCA [(1) से]
CA = AC [उभयनिष्ठ]
∠BCA = ∠DAC [(2) से]
∴ ∆ABC ≅ ∆CDA [ASA सर्वांगसमता से]
प्रश्न 5.
रेखा l, ∠A का समद्विभाजक है और ∠B, l पर स्थित कोई भी बिंदु है। BP और BQ, B से LA की भुजाओं पर लंब हैं (चित्र देखें)। दर्शाइए कि
(i) ∆APB ≅ ∆AQB
(ii) BP = BQ या B, ∠A की भुजाओं से समान दूरी पर है।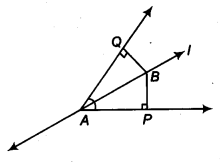
हल:
∠QAP का समद्विभाजक l है।
∴ ∠QAB = ∠PAB
∠Q = ∠P [प्रत्येक 90°]
∠ABQ = ∠ABP
[A के कोण योग गुण से]
अब, ∆APB और ∆AQB में, हमारे पास है
∠ABP = ∠ABQ [ऊपर सिद्ध]
AB = BA [उभयनिष्ठ]
∠PAB = ∠QAB [दिया गया है]
∴ ∆APB ≅ ∆AQB [ASA सर्वांगसमता से]
क्योंकि ∆APB ≅ ∆AQB
⇒ BP = BQ [CPCT से]
अर्थात, [AP से B की लंबवत दूरी]
= [AQ से B की लंबवत दूरी]
इस प्रकार, बिंदु B, ∠A की भुजाओं से समान दूरी पर है।
प्रश्न 6.
आकृति में, AC = AE, AB = AD और ∠BAD = ∠EAC. दर्शाइए कि BC = DE.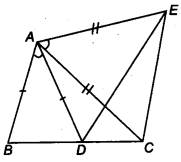
हल:
∠BAD = ∠EAC
दोनों पक्षों में ∠DAC जोड़ने पर,
∠BAD + ∠DAC = ∠EAC + ∠DAC
⇒ ∠BAC = ∠DAE
अब, ∆ABC और ∆ADE में,
∠BAC = ∠DAE [ऊपर सिद्ध]
AB = AD [दिया गया है]
AC = AE [दिया गया है]
∴ ∆ABC ≅ ∆ADE [SAS सर्वांगसमता से]
⇒ BC = DE [CPCT से]
प्रश्न 7.
AS एक रेखाखंड है और P इसका मध्य-बिंदु है। D और E, AB के एक ही ओर स्थित बिंदु इस प्रकार हैं कि ∠ BAD = ∠ ABE और ∠ EPA = ∠ DPB है। (आकृति देखें)। दर्शाइए कि
(i) ∆DAP ≅ ∆EBP
(ii) AD = BE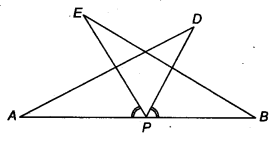
हल:
P, AB का मध्य-बिंदु है।
∴ AP = BP
∠EPA = ∠DPB [दिया है]
दोनों ओर ∠EPD जोड़ने पर, हम प्राप्त करते हैं:
∠EPA + ∠EPD = ∠DPB + ∠EPD
⇒ ∠APD = ∠BPE
(i) अब, ∆DAP और ∆EBP में, हमारे पास है
∠PAD = ∠PBE [ ∵∠BAD = ∠ABE]
AP = BP [ऊपर सिद्ध]
∠DPA = ∠EPB [ऊपर सिद्ध]
∴ ∆DAP ≅ ∆EBP [ASA सर्वांगसमता से]
(ii) चूँकि, ∆ DAP ≅ ∆ EBP
⇒ AD = BE [CPCT द्वारा]
Ex 7.2
प्रश्न 1.
एक समद्विबाहु त्रिभुज ABC में, जिसमें AB = AC है, ∠B और ∠C के समद्विभाजक एक दूसरे को O पर प्रतिच्छेद करते हैं। A को O से मिलाइए। दर्शाइए कि
(i) OB = OC
(ii) AO, ∠A को समद्विभाजित करता है।
हल:
i) ∆ABC में,
AB = AC [दिया है]
∴ ∠ABC = ∠ACB [A की समान भुजाओं के सम्मुख कोण बराबर होते हैं]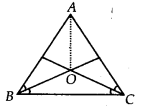
⇒
या ∠OBC = ∠OCB
⇒ OC = OB [∆ के बराबर कोणों के विपरीत भुजाएँ बराबर होती हैं]
(ii) ∆ABO और ∆ACO में,
AB = AC [दिया है]
∠OBA = ∠OCA [ ∵
OB = OC [ऊपर सिद्ध]
∆ABO ≅ ∆ACO [SAS सर्वांगसमता द्वारा]
⇒ ∠OAB = ∠OAC [CPCT द्वारा]
⇒ AO, ∠A को समद्विभाजित करता है।
प्रश्न 2.
∆ABC में, AD, BC का लंब समद्विभाजक है (चित्र देखें)। दर्शाइए कि ∆ ABC एक समद्विबाहु त्रिभुज है जिसमें AB = AC है।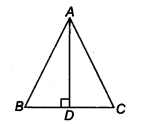
हल:
चूँकि AD, BC का समद्विभाजक है।
∴ BD = CD
अब, ∆ABD और ∆ACD में,
AD = DA [उभयनिष्ठ]
∠ADB = ∠ADC [प्रत्येक 90°]
BD = CD [ऊपर सिद्ध]
∴ ∆ABD ≅ ∆ACD [SAS सर्वांगसमता से]
⇒ AB = AC [CPCT से]
इस प्रकार, ∆ABC एक समद्विबाहु त्रिभुज है।
प्रश्न 3.
ABC एक समद्विबाहु त्रिभुज है जिसमें शीर्षलंब BE और CF क्रमशः बराबर भुजाओं AC और AB पर खींचे गए हैं (चित्र देखें)। दर्शाइए कि ये शीर्षलंब बराबर हैं।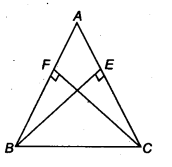
हल:
∆ABC एक समद्विबाहु त्रिभुज है।
∴ AB = AC
⇒ ∠ACB = ∠ABC [A की बराबर भुजाओं के सम्मुख कोण बराबर होते हैं]
⇒ ∠BCE = ∠CBF
अब, ∆BEC और ∆CFB में
∠BCE = ∠CBF [ऊपर सिद्ध]
∠BEC = ∠CFB [प्रत्येक 90°]
BC = CB [उभयनिष्ठ]
∴ ∆BEC ≅ ∆CFB [AAS सर्वांगसमता से]
अतः, BE = CF [CPCT से]
प्रश्न 4.
ABC एक त्रिभुज है जिसमें भुजाओं AC और AB के शीर्षलंब BE और CF बराबर हैं (चित्र देखें)।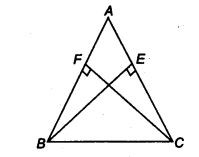
दर्शाइए कि
(i) ∆ABE ≅ ∆ACF
(ii) AB = AC अर्थात्, ABC एक समद्विबाहु त्रिभुज है।
हल:
(i) ∆ABE और ∆ACE में,
∠AEB = ∠AFC
[प्रत्येक 90° है क्योंकि BE ⊥ AC और CF ⊥ AB]
∠A = ∠A [उभयनिष्ठ]
BE = CF [दिया है]
∴ ∆ABE ≅ ∆ACF [AAS सर्वांगसमता से]
(ii) चूँकि, ∆ABE ≅ ∆ACF
∴ AB = AC [CPCT से]
⇒ ABC एक समद्विबाहु त्रिभुज है।
प्रश्न 5.
∆ABC एक समद्विबाहु त्रिभुज है जिसमें AB = AC है। भुजा BA को D तक इस प्रकार बढ़ाया गया है कि AD = AB है (चित्र देखें)। दर्शाइए कि ∠BCD एक समकोण है।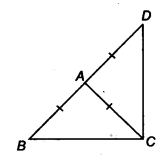
हल:
AB = AC [दिया गया है] …(1)
AB = AD [दिया गया है] …(2)
(1) और (2) से, हमारे पास
AC = AD है
अब, ∆ABC में, हमारे पास
∠ABC + ∠ACB + ∠BAC = 180° है [A का कोण योग गुण]
⇒ 2∠ACB + ∠BAC = 180° …(3)
[∠ABC = ∠ACB (A की बराबर भुजाओं के विपरीत कोण बराबर होते हैं)]
इसी प्रकार, ∆ACD में,
∠ADC + ∠ACD + ∠CAD = 180°
⇒ 2∠ACD + ∠CAD = 180° …(4)
[∠ADC = ∠ACD (A की बराबर भुजाओं के विपरीत कोण बराबर होते हैं)]
(3) और को जोड़ने पर (4), हमारे पास है
2∠ACB + ∠BAC + 2 ∠ACD + ∠CAD = 180° +180°
⇒ 2[∠ACB + ∠ACD] + [∠BAC + ∠CAD] = 360°
⇒ 2∠BCD +180° = 360° [∠BAC और ∠CAD एक रैखिक युग्म बनाते हैं]
⇒ 2∠BCD = 360° – 180° = 180°
⇒ ∠BCD =
इस प्रकार, ∠BCD = 90°
प्रश्न 6.
ABC एक समकोण त्रिभुज है जिसमें ∠A = 90° और AB = AC है, ∠B और ∠C ज्ञात कीजिए।
हल:
∆ABC में, AB = AC [दिया है]
∴ उनके सम्मुख कोण बराबर हैं।
⇒ ∠ACB = ∠ABC
अब, ∠A + ∠B + ∠C = 180°
[∠A = 90°(दिया है)]
⇒ ∠B + ∠C= 180°- 90° = 90°
लेकिन ∠B = ∠C
∠B = ∠C =
इस प्रकार, ∠B = 45° और ∠C = 45°
प्रश्न 7.
दर्शाइए कि एक समबाहु त्रिभुज के प्रत्येक कोण 60° के होते हैं।
हल:
∆ABC में,
AB = BC = CA
[ABC एक समबाहु त्रिभुज है]
AB = BC
⇒ ∠A = ∠C …(1) [A के बराबर भुजाओं के सम्मुख कोण बराबर होते हैं]
इसी प्रकार, AC = BC
⇒ ∠A = ∠B …(2)
(1) और (2) से,
∠A = ∠B = ∠C = x (मान लीजिए)
चूँकि, ∠A + ∠B + ∠C = 180° [A का कोण योग गुण]
∴ x + x + x = 180o
⇒ 3x = 180°
⇒ x = 60°
∴ ∠A = ∠B = ∠C = 60°
इस प्रकार, एक समबाहु त्रिभुज के प्रत्येक कोण 60° के होते हैं।
Ex 7.3
प्रश्न 1.
∆ABC और ∆DBC एक ही आधार BC पर स्थित दो समद्विबाहु त्रिभुज हैं तथा शीर्ष A और D, BC के एक ही ओर हैं (चित्र देखें)। यदि AD को बढ़ाकर BC को P पर प्रतिच्छेद किया जाए, तो दर्शाइए कि
(i) ∆ABD ≅ ∆ACD
(ii) ∆ABP ≅ ∆ACP
(iii) AP, ∠A के साथ-साथ ∠D को भी समद्विभाजित करता है।
(iv) AP, BC का लंब समद्विभाजक है।
हल:
(i) ∆ABD और ∆ACD में,
AB = AC [दिया गया है]
AD = DA [उभयनिष्ठ]
BD = CD [दिया गया है]
∴ ∆ABD ≅ ∆ACD [SSS सर्वांगसमता से]
∠BAD = ∠CAD [CPCT से] …(1)
(ii) ∆ABP और ∆ACP में,
AB = AC [दिया है]
∠BAP = ∠CAP [(1) से]
∴ AP = PA [उभयनिष्ठ]
∴ ∆ABP ≅ ∆ACP [SAS सर्वांगसमता से]
(iii) चूँकि, ∆ABP ≅ ∆ACP
⇒ ∠BAP = ∠CAP [CPCT द्वारा]
∴ AP, ∠A का समद्विभाजक है।
पुनः, ∆BDP और ∆CDP में,
हमारे पास है BD = CD [दिया गया है]
DP = PD [उभयनिष्ठ]
BP = CP [ ∵ ∆ABP ≅ ∆ACP]
⇒ A BDP = ACDP [SSS सर्वांगसमता द्वारा]
∴ ∠BDP = ∠CDP [CPCT द्वारा]
⇒ DP (या AP) ∠BDC का समद्विभाजक है
∴ AP, ∠A के साथ-साथ ∠D का भी समद्विभाजक है।
(iv) चूँकि, ∆ABP ≅ ∆ACP
⇒ ∠APS = ∠APC, BP = CP [CPCT द्वारा]
लेकिन ∠APB + ∠APC = 180° [रैखिक युग्म]
∴ ∠APB = ∠APC = 90°
⇒ AP ⊥ BC, BP = CP भी
अतः, AP, BC का लम्ब समद्विभाजक है।
प्रश्न 2.
AD एक समद्विबाहु त्रिभुज ABC का शीर्षलंब है जिसमें AB = AC है। दर्शाइए कि
(i) AD, BC को समद्विभाजित करता है
(ii) AD, ∠A को समद्विभाजित करता है।
हल:
(i) समकोण ∆ABD और ∆ACD में,
AB = AC [दिया है]
∠ADB = ∠ADC [प्रत्येक 90°]
AD = DA [उभयनिष्ठ]
∴ ∆ABD ≅ ∆ACD [दाहिनी ओर सर्वांगसमता से]
अतः, BD = CD [CPCT से]
⇒ D, BC का मध्य-बिंदु है या AD, BC को समद्विभाजित करता है।
(ii) चूँकि, ∆ABD ≅ ∆ACD,
⇒ ∠BAD = ∠CAD [CPCT द्वारा]
अतः, AD, ∠A को समद्विभाजित करता है
प्रश्न 3.
एक त्रिभुज ABC की दो भुजाएँ AB और BC तथा माध्यिका AM क्रमशः ∆PQR की भुजाओं PQ और OR तथा माध्यिका PN के बराबर हैं (चित्र देखें)। दर्शाइए कि
(i) ∆ABC ≅ ∆PQR
(ii) ∆ABM ≅ ∆PQN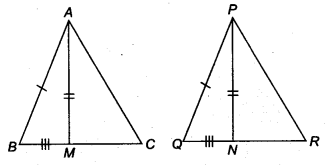
हल:
∆ABC में, AM माध्यिका है।
∴BM =
∆PQR में, PN माध्यिका है।
∴ QN =
और BC = QR [दिया गया है]
⇒
⇒ BM = QN …(3) [(1) और (2) से]
(i) ∆ABM और ∆PQN में,
AB = PQ, [दिया है]
AM = PN [दिया है]
BM = QN [(3) से]
∴ ∆ABM ≅ ∆PQN [SSS सर्वांगसमता से]
(ii) चूँकि ∆ABM ≅ ∆PQN
⇒ ∠B = ∠Q …(4) [CPCT से]
अब, ∆ABC और ∆PQR में,
∠B = ∠Q [(4) से]
AB = PQ [दिया गया है]
BC = QR [दिया गया है]
∴ ∆ABC ≅ ∆PQR [SAS सर्वांगसमता से]
प्रश्न 4.
BE और CF एक त्रिभुज ABC के दो बराबर शीर्षलंब हैं। RHS सर्वांगसमता नियम का प्रयोग करके सिद्ध कीजिए कि त्रिभुज ABC समद्विबाहु है।
हल:
चूंकि BE ⊥ AC [दिया गया है]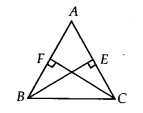
∴ BEC एक समकोण त्रिभुज है जिससे ∠BEC = 90°
इसी प्रकार, ∠CFB = 90°
अब, समकोण ∆BEC और ∆CFB में, हमारे पास है
BE = CF [दिया गया है]
BC = CB [उभयनिष्ठ कर्ण]
∠BEC = ∠CFB [प्रत्येक 90°]
∴ ∆BEC ≅ ∆CFB [RHS सर्वांगसमता से]
तो, ∠BCE = ∠CBF [CPCT से]
या ∠BCA = ∠CBA
अब, ∆ABC में, ∠BCA = ∠CBA
⇒ AB = AC [∆ के बराबर कोणों के विपरीत भुजाएँ बराबर होती हैं]
∴ ABC एक समद्विबाहु त्रिभुज है।
प्रश्न 5.
ABC एक समद्विबाहु त्रिभुज है जिसमें AB = AC है। AP ⊥ BC खींचकर दर्शाइए कि ∠B = ∠C है।
हल:
AP ⊥ BC [दिया है]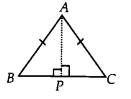
∠APB = 90° और ∠APC = 90°
∆ABP और ∆ACP में,
∠APB = ∠APC [प्रत्येक 90°]
AB = AC [दिया है]
AP = AP [उभयनिष्ठ]
∴ ∆ABP ≅ ∆ACP [दाहिनी ओर सर्वांगसमता से]
अतः, ∠B = ∠C [CPCT से]
Ex 7.4
प्रश्न 1.
दर्शाइए कि समकोण त्रिभुज में कर्ण सबसे लंबी भुजा होती है।
हल:
आइए ∆ABC लें जिससे ∠B = 90°
∴ ∠A + ∠B + ∠C = 180°
⇒ ∠A + 90°-+ ∠C = 180°
⇒ ∠A + ∠C = 90°
⇒∠A + ∠C = ∠B
∴ ∠B > ∠A और ∠B > ∠C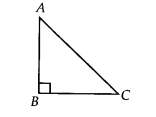
⇒ ∠B के विपरीत भुजा ∠A के विपरीत भुजा से लंबी है
अर्थात AC > BC।
इसी प्रकार, AC > AB।
इसलिए, AC सबसे लंबी भुजा है। लेकिन AC त्रिभुज का कर्ण है। इस प्रकार, कर्ण सबसे लम्बी भुजा है।
प्रश्न 2.
आकृति में, ∆ABC की भुजाएँ AB और AC क्रमशः बिंदु P और Q तक बढ़ाई गई हैं। साथ ही, ∠PBC < ∠QCB है। दर्शाइए कि AC > AB है।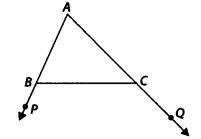
हल:
∠ABC + ∠PBC = 180° [रैखिक युग्म]
और ∠ACB + ∠QCB = 180° [रैखिक युग्म]
लेकिन ∠PBC < ∠QCB [दिया है] ⇒ 180° – ∠PBC > 180° – ∠QCB
⇒ ∠ABC > ∠ACB
∠ABC के विपरीत भुजा > ∠ACB के विपरीत भुजा
⇒ AC > AB है।
प्रश्न 3.
आकृति में, ∠B <∠A और ∠C <∠D. दर्शाइए कि AD < BC.
हल: चूँकि ∠A > ∠B [दिया है]
∴ OB > OA …(1)
[बड़े कोण के सामने वाली भुजा लंबी होती है]
इसी प्रकार, OC > OD …(2)
(1) और (2) को जोड़ने पर,
OB + OC > OA + OD
⇒ BC > AD
प्रश्न 4.
AB और CD क्रमशः एक चतुर्भुज ABCD की सबसे छोटी और सबसे लंबी भुजाएँ हैं (चित्र देखें)। दर्शाइए कि ∠A > ∠C और ∠B > ∠D है।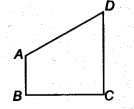
हल:
आइए AC को मिलाएँ।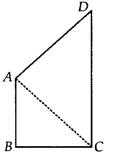
अब, ∆ABC में, AB < BC [∵ चतुर्भुज ABCD की सबसे छोटी भुजा AB है] ⇒ BC > AB
⇒ ∠BAC > ∠BCA …(1)
[A की लंबी भुजा के विपरीत कोण बड़ा होता है]
पुनः, ∆ACD में, CD > AD
[CD चतुर्भुज ABCD की सबसे लंबी भुजा CD है]
⇒ ∠CAD > ∠ACD …(2)
[∆ की लंबी भुजा के विपरीत कोण बड़ा होता है]
(1) और (2) को जोड़ने पर, हम पाते हैं
∠BAC + ∠CAD > ∠BCA + ∠ACD
⇒ ∠A > ∠C
इसी प्रकार, BD को जोड़ने पर, हम पाते हैं ∠B > ∠D
प्रश्न 5.
आकृति में, PR > PQ और PS, ∠QPR को समद्विभाजित करते हैं। सिद्ध कीजिए कि ∠PSR > ∠PSQ है।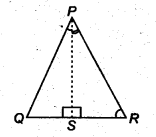
हल:
∆PQR में, PS, ∠QPR को समद्विभाजित करता है [दिया गया है]
∴ ∠QPS = ∠RPS
और PR > PQ [दिया गया है]
⇒ ∠PQS > ∠PRS [A की लंबी भुजा के विपरीत कोण बड़ा है]
⇒ ∠PQS + ∠QPS > ∠PRS + ∠RPS …(1) [∵∠QPS = ∠RPS]
∵ बाह्य ∠PSR = [∠PQS + ∠QPS]
और बाह्य ∠PSQ = [∠PRS + ∠RPS]
[एक बाह्य कोण आंतरिक विपरीत कोणों के योग के बराबर होता है]
अब, (1) से, हमारे पास
∠PSR = ∠PSQ है।
प्रश्न 6.
दर्शाइए कि किसी दिए गए बिंदु से, जो उस पर स्थित नहीं है, खींचे गए सभी रेखाखंडों में से, लंब रेखाखंड सबसे छोटा होता है।
हल:
आइए ∆PMN लें जिससे ∠M = 90° है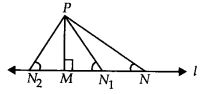
क्योंकि, ∠M + ∠N + ∠P = 180°
[त्रिभुज के कोणों का योग 180° होता है]
∵ ∠M = 90° [PM ⊥ l]
अतः, ∠N + ∠P = ∠M
⇒ ∠N < ∠M
⇒ PM < PN …(1)
इसी प्रकार, PM < PN 1 …(2)
और PM < PN 2 …(3)
(1), (2) और (3) से, हम पाते हैं कि PM, P से रेखा l पर खींचा गया सबसे छोटा रेखाखंड है। इस प्रकार, लंब रेखाखंड किसी रेखा पर उस बिंदु से खींचा गया सबसे छोटा रेखाखंड होता है जो उस रेखा पर नहीं होता।
Ex 7.5
प्रश्न 1.
∆ABC एक त्रिभुज है। ∆ABC के अभ्यंतर में एक बिंदु ज्ञात कीजिए जो ∆ABC के सभी शीर्षों से समान दूरी पर हो।
हल:
आइए एक ∆ABC लें।
AB का लंब समद्विभाजक l खींचिए।
BC का लंब समद्विभाजक m खींचिए।
मान लीजिए कि दोनों लंब समद्विभाजक l और m बिंदु O पर मिलते हैं।
O अभीष्ट बिंदु है जो A, B और C से समान दूरी पर है।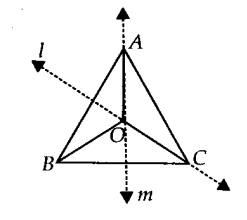
नोट: यदि हम केंद्र O और त्रिज्या OB या OC लेकर एक वृत्त खींचते हैं, तो यह A, B और C से होकर गुजरेगा। बिंदु O को त्रिभुज का परिकेन्द्र कहते हैं।
प्रश्न 2.
एक त्रिभुज के अभ्यंतर में एक बिंदु ज्ञात कीजिए जो त्रिभुज की सभी भुजाओं से समान दूरी पर हो।
हल:
आइए एक ∆ABC लें।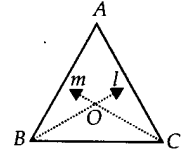
∠C का समद्विभाजक m खींचिए।
मान लीजिए कि दोनों समद्विभाजक l और m, बिंदु O पर मिलते हैं।
इस प्रकार, O अभीष्ट बिंदु है जो ∆ABC की भुजाओं से समान दूरी पर है।
नोट: यदि हम OM ⊥ BC खींचते हैं और O को केंद्र और OM को त्रिज्या मानकर एक वृत्त खींचते हैं, तो वृत्त त्रिभुज की भुजाओं को स्पर्श करेगा। बिंदु O को त्रिभुज का अंतःकेंद्र कहते हैं।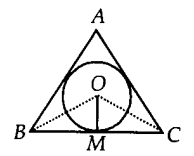
प्रश्न 3.
एक विशाल पार्क में, लोग तीन बिंदुओं पर एकत्रित हैं (चित्र देखें)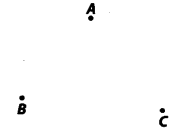
A: जहाँ बच्चों के लिए अलग-अलग स्लाइड और झूले हैं।
B: जिसके पास एक मानव निर्मित झील स्थित है।
C: जो एक बड़ी पार्किंग के पास है और मौजूद है।
आइसक्रीम पार्लर कहाँ स्थापित किया जाना चाहिए ताकि अधिकतम संख्या में लोग वहां पहुंच सकें?
[संकेत: पार्लर A, B और C से समान दूरी पर होना चाहिए।]
हल:
आइए A और B को मिलाएं, और AB का लंब द्विभाजक l खींचें।
अब, B और C को मिलाएं, और BC का लंब द्विभाजक m खींचें। मान लें कि लंब द्विभाजक l और m O पर मिलते हैं।
बिंदु O वह आवश्यक बिंदु है जहां आइसक्रीम पार्लर स्थापित किया जाना है।
नोट: यदि हम A और C को जोड़ते हैं और लंब द्विभाजक खींचते हैं, तो यह बिंदु O से भी मिलेगा (या गुजरेगा)।
प्रश्न 4.
षट्कोणीय और ताराकार रंगोली [देखिए आकृति (i) और (ii)] को 1 सेमी भुजा वाले जितने समबाहु त्रिभुज भर सकते हैं, भरकर पूरा कीजिए। प्रत्येक स्थिति में त्रिभुजों की संख्या गिनिए। किसमें ज़्यादा त्रिभुज हैं?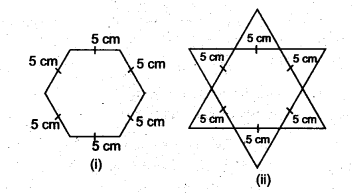
हल:
यह एक क्रियाकलाप है।
हमें आकृति (i) में 1 सेमी भुजा वाले 150 समबाहु त्रिभुज और आकृति (ii) में 300 समबाहु त्रिभुज चाहिए।
∴ आकृति (ii) में ज़्यादा त्रिभुज हैं।
