SikhLo - Current Affairs in Hindi, Daily current affairs, Current affairs

NCERT कक्षा 6 गणित अध्याय 5 प्रारंभिक आकृतियों को समझना

Ex 5.1

प्रश्न 1.
मीटर प्रेक्षण द्वारा रेखाखंडों की तुलना करने में क्या हानि है?
हल:
केवल 'प्रेक्षण' द्वारा दो रेखाखंडों की लंबाई की तुलना सटीक नहीं हो सकती है। इसलिए हम दिए गए रेखाखंडों की लंबाई की तुलना करने के लिए विभाजक का उपयोग करते हैं।

प्रश्न 2.
किसी रेखाखंड की लंबाई मापते समय रूलर की बजाय डिवाइडर का उपयोग करना बेहतर क्यों होता है?
हल:
रूलर का उपयोग करके रेखाखंड की लंबाई मापते समय, हमें निम्नलिखित त्रुटियाँ हो सकती हैं:
(i) रूलर की मोटाई
(ii) कोणीय दृश्यता।
इन त्रुटियों को डिवाइडर का उपयोग करके दूर किया जा सकता है। इसलिए, रेखाखंड की लंबाई मापते समय रूलर की बजाय डिवाइडर का उपयोग करना बेहतर होता है।

प्रश्न 3.
कोई रेखाखंड खींचिए, मान लीजिए AB¯¯¯¯¯¯¯¯। A और B के बीच स्थित कोई बिंदु C लीजिए। AB, BC और AC की लंबाई मापिए। क्या AB = AC + CB है?
[नोट: यदि A, B, C एक रेखा पर कोई तीन बिंदु हैं जैसे AC + CB = AB, तो हम सुनिश्चित हो सकते हैं कि C, A और B के बीच स्थित है]
हल:
आइए

A, B और C पर विचार करें जिससे C, A और B के बीच स्थित है और AB = 7 सेमी है।
AC = 3 सेमी, CB = 4 सेमी है।
∴ AC + CB = 3 सेमी + 4 सेमी = 7 सेमी।
लेकिन, AB = 7 सेमी है।
इसलिए, AB = AC + CB।

प्रश्न 4.
यदि A, B, C एक रेखा पर तीन बिंदु इस प्रकार हैं कि AB = 5 सेमी, BC = 3 सेमी और AC = 8 सेमी, तो उनमें से कौन सा बिंदु अन्य दो बिंदुओं के बीच स्थित है?
हल:
AB = 5 सेमी; BC = 3 सेमी
∴ AB + BC = 5 + 3 = 8 सेमी
लेकिन, AC = 8 सेमी
अतः, B, A और C के बीच स्थित है।

प्रश्न 5.
सत्यापित कीजिए कि क्या D, 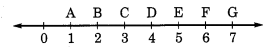AG¯¯¯¯¯¯¯¯ का मध्य बिंदु है।

हल:
दी गई आकृति से, हमें प्राप्त होता है
AG = 7 सेमी – 1 सेमी = 6 सेमी
AD = 4 सेमी – 1 सेमी = 3 सेमी
और DG = 7 सेमी – 4 सेमी = 3 सेमी
∴ AG = AD + DG।
अतः, D, AG¯¯¯¯¯¯¯¯ का मध्य बिंदु है।

प्रश्न 6.
यदि B, AC¯¯¯¯¯¯¯¯ का मध्य बिंदु है और C, BD¯¯¯¯¯¯¯¯ का मध्य बिंदु है, जहाँ A, B, C, D एक सीधी रेखा पर स्थित हैं, तो बताइए AB = CD क्यों है?
हल:
B,

AC¯¯¯¯¯¯¯¯ का मध्य बिंदु है।
∴ AB = BC …(i)
C, BD¯¯¯¯¯¯¯¯ का मध्य बिंदु है।
BC = CD
समीकरण (i) और (ii) से,
AB = CD

प्रश्न 7.
पाँच त्रिभुज बनाइए और उनकी भुजाएँ मापिए। प्रत्येक स्थिति में जाँच कीजिए कि क्या किन्हीं दो भुजाओं की लंबाई का योग हमेशा तीसरी भुजा से कम होता है।
हल:
स्थिति I. ∆ABC में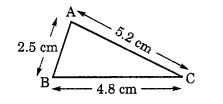

मान लीजिए AB = 2.5 सेमी
BC = 4.8 सेमी
और AC = 5.2 सेमी
AB + BC = 2.5 सेमी + 4.8 सेमी
= 7.3 सेमी
क्योंकि, 7.3 > 5.2
अतः, AB + BC > AC
अतः, त्रिभुज की किन्हीं दो भुजाओं का योग तीसरी भुजा से अधिक होता है।

स्थिति II. ∆PQR में,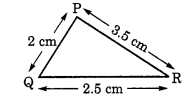

मान लीजिए PQ = 2 सेमी
QR = 2.5 सेमी
और PR = 3.5 सेमी
PQ + QR = 2 सेमी + 2.5 सेमी = 4.5 सेमी
क्योंकि, 4.5 > 3.5
इसलिए, PQ + QR > PR
इसलिए, त्रिभुज की किसी भी दो भुजाओं का योग तीसरी भुजा से अधिक होता है।

स्थिति III. ∆XYZ में,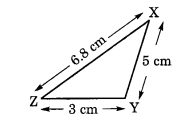

मान लीजिए XY = 5 सेमी
YZ = 3 सेमी
और ZX = 6.8 सेमी
XY + YZ = 5 सेमी + 3 सेमी
= 8 सेमी
क्योंकि, 8 > 6.8
इसलिए, XY + YZ > ZX
इसलिए, त्रिभुज की किसी भी दो भुजाओं का योग तीसरी भुजा से अधिक होता है।

स्थिति IV. ∆MNS में,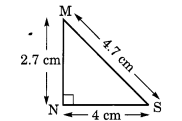

मान लीजिए MN = 2.7 सेमी
NS = 4 सेमी
MS = 4.7 सेमी
और MN + NS = 2.7 सेमी + 4 सेमी = 6.7 सेमी
क्योंकि, 6.7 >4.7
इसलिए, MN + NS > MS
इसलिए, त्रिभुज की किसी भी दो भुजाओं का योग तीसरी भुजा से अधिक होता है।

केस V. ∆KLM में,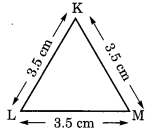

मान लीजिए KL = 3.5 सेमी
LM = 3.5 सेमी
KM = 3.5 सेमी
और KL + LM = 3.5 सेमी + 3.5 सेमी = 7 सेमी
7 सेमी > 3.5 सेमी
हल:
(i) एक-चौथाई चक्कर के लिए, हमारे पास है
इसलिए, KL + LM > KM
अतः, त्रिभुज की किन्हीं दो भुजाओं का योग तीसरी भुजा से अधिक होता है।
अतः, हम यह निष्कर्ष निकालते हैं कि त्रिभुज की किन्हीं दो भुजाओं का योग कभी भी तीसरी भुजा से कम नहीं होता है।

Ex 5.2

प्रश्न 1.
एक घड़ी की घंटे की सुई दक्षिणावर्त दिशा में कितने भाग घूमेगी, जब वह
(a) 3 से 9 तक
(b) 4 से 7 तक
(c) 7 से 10 तक
(d) 12 से 9 तक
(e) 1 से 10 तक
(f) 6 से 3 तक
हल:
(a) 3 से 9 तक
9 – 3 = 6 ÷ 12 = \(\frac { 1 }{ 2 }\) चक्कर12 of a revolution

(b) 4 से 7
7 – 4 = 3 ÷ 12 = \(\frac { 1 }{ 4 }\) एक चक्कर14 of a revolution

(c) 7 से 10
10 – 7 = 3 ÷ 12 = \(\frac { 1 }{ 4 }\) एक चक्कर14 of a revolution

(d) 12 से 9 अर्थात, 0 से 9
9 – 0 = 9 ÷ 12 = \(\frac { 3 }{ 4 }\) एक चक्कर34 of a revolution

(e) 1 से 10
10 – 1 = 9 ÷ 12 = \(\frac { 3 }{ 4 }\) एक चक्कर का34 of a revolution

(f) 6 से 3 अर्थात, 6 से 12 और फिर 12 से 3
6 से 12 = 12 – 6 = 6 और 12 से 3 = 0 से 3 = 3 – 0 = 3
6 + 3 = 9 ÷ 12 = \(\frac { 3 }{ 4 }\) एक चक्कर34 of a revolution

प्रश्न 2.
एक घड़ी की सुई कहाँ रुकेगी यदि यह
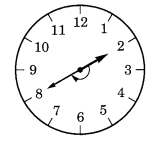
(a) 12 से शुरू होकर दक्षिणावर्त दिशा में \(\frac { 1 }{ 2 }\) चक्कर लगाती है? (b) 2 से शुरू होकर दक्षिणावर्त दिशा में \(\frac { 1 }{ 2 }\) चक्कर लगाती है? (c) 5 से शुरू होकर दक्षिणावर्त दिशा में \(\frac { 1 }{ 2 }\) चक्कर लगाती है? (d) 5 से शुरू होकर दक्षिणावर्त दिशा में \(\frac { 1 }{ 2 }\) चक्कर लगाती है? 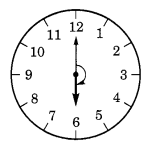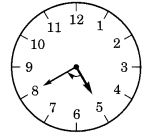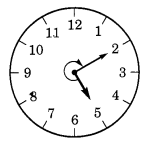हल: (a) 12 से शुरू करके और \(\frac { 1 }{ 2 }\) चक्कर लगाने पर, घड़ी की सुई 6 पर रुक जाती है। (b) 2 से शुरू करके और \(\frac { 1 }{ 2 }\) चक्कर लगाने पर, घड़ी की सुई 8 पर रुक जाती है। (c) 5 से शुरू करके और \(\frac { 1 }{ 2 }\) चक्कर लगाने पर, घड़ी की सुई 8 पर रुक जाती है। (d) 5 से शुरू करके और \(\frac { 1 }{ 2 }\) चक्कर लगाने पर, घड़ी की सुई 2 पर रुक जाती है।12 of a revolution, clockwise?
12 of a revolution, clockwise?
12 of a revolution, clockwise?
12 of a revolution, clockwise?

12 of a revolution, the clock hand stops at 6.

12 of a revolution, the clock hand stops at 8.

12 of a revolution, the clock hand stops at 8.

12 of a revolution, the clock hand stops at 2.

प्रश्न 3.
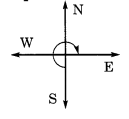
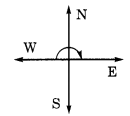
यदि आप
(a) पूर्व की ओर मुंह करके चलना शुरू करते हैं और दक्षिणावर्त दिशा में \(\frac { 1 }{ 2 }\) चक्कर लगाते हैं, तो आप किस दिशा के सम्मुख होंगे? ( b) पूर्व की ओर मुंह करके चलना शुरू करते हैं और दक्षिणावर्त दिशा में \(\frac { 1 }{ 2 }\) चक्कर लगाते हैं? (c) पश्चिम की ओर मुंह करके चलना शुरू करते हैं और वामावर्त दिशा में \(\frac { 3 }{ 4 }\) चक्कर लगाते हैं? (d) दक्षिण की ओर मुंह करके चलना शुरू करते हैं और एक पूरा चक्कर लगाते हैं? (क्या हमें इस अंतिम प्रश्न के लिए दक्षिणावर्त या वामावर्त निर्दिष्ट करना चाहिए? क्यों नहीं?) हल: एक पूरा चक्कर लगाने पर हम मूल (प्रारंभिक) स्थिति पर वापस पहुंच जाएंगे। इसलिए, इससे कोई फर्क नहीं पड़ता कि हम दक्षिणावर्त या वामावर्त घूमते हैं।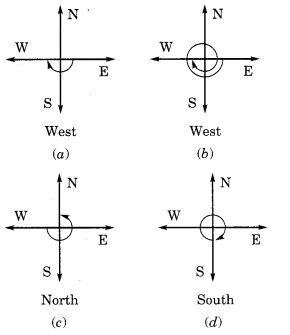12 of a revolution clockwise? z
112 of a revolution clockwise? z
34 of a revolution anticlockwise?

प्रश्न 4.
यदि आप
(a) पूर्व की ओर मुख करके खड़े हैं और उत्तर की ओर दक्षिणावर्त घूमकर खड़े हैं?
(b) दक्षिण की ओर मुख करके खड़े हैं और पूर्व की ओर दक्षिणावर्त घूमकर खड़े हैं?
(c) पश्चिम की ओर मुख करके खड़े हैं और पूर्व की ओर दक्षिणावर्त घूमकर खड़े हैं?
हल:
(a) यदि हम पूर्व से शुरू करते हैं और उत्तर में पहुँचते हैं (दक्षिणावर्त घूमकर) तो \(\frac { 3 }{ 4 }\) चक्कर लगाना पड़ता है। (b) यदि हम दक्षिण से शुरू करते हैं और पूर्व की ओर दक्षिणावर्त घूमकर खड़े हैं, तो \(\frac { 3 }{ 4 }\) चक्कर लगाना पड़ता है। (c) यदि हम पश्चिम से शुरू करते हैं और पूर्व की ओर दक्षिणावर्त घूमकर खड़े हैं, तो \(\frac { 1 }{ 2 }\) चक्कर लगाना पड़ता है।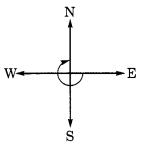34 of a revolution is required.

34 of a revolution is required.

12 of a revolution is required.

प्रश्न 5.
एक घड़ी की घंटे की सुई द्वारा बनाए गए समकोण की संख्या ज्ञात कीजिए जब यह
(a) 3 से 6 तक जाती है
(b) 2 से 8 तक
(c) 5 से 11 तक
(d) 10 से 1 तक
(e) 12 से 9 तक
(f) 12 से 6 तक
हल:
(a) 3 से 6 तक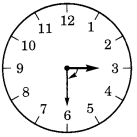

3 से 6 तक शुरू करते हुए, घंटे की सुई 1 समकोण घूमती है।

(b) 2 से 8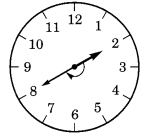

2 से 8 तक प्रारंभ करते हुए, घंटे की सुई 2 समकोण पर घूमती है।

(c) 5 से 11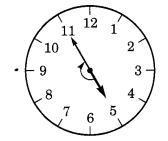

5 से 11 तक शुरू करते हुए, घंटे की सुई 2 समकोण पर घूमती है।

(d) 10 से 1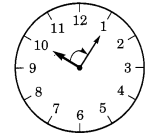

10 से 1 तक शुरू करने पर, घंटे की सुई 1 समकोण पर घूमती है।

(ई) 12 से 9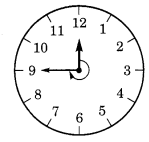

12 से 9 तक शुरू करते हुए, घंटे की सुई 3 समकोण घूमती है।

(च) 12 से 6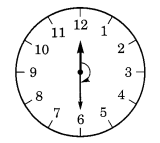

12 से 6 तक शुरू करते हुए, घंटे की सुई 2 समकोण पर घूमती है।

प्रश्न 6.
यदि आप
(a) दक्षिण की ओर मुँह करके पश्चिम की ओर घड़ी की दिशा में मुड़ते हैं?
(b) उत्तर की ओर मुँह करके पूर्व की ओर घड़ी की विपरीत दिशा में मुड़ते हैं?
(c) पश्चिम की ओर मुँह करके पश्चिम की ओर मुड़ते हैं? (
d) दक्षिण की ओर मुँह करके उत्तर की ओर मुड़ते हैं, तो आप कितने समकोण बनाते हैं?
हल: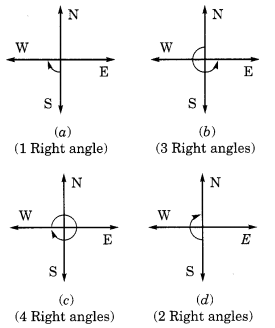

प्रश्न 7.
एक घड़ी की घंटे की सुई कहाँ रुकेगी यदि यह
(a) 6 से शुरू होकर 1 समकोण घूमे?
(b) 8 से शुरू होकर 2 समकोण घूमे?
(c) 10 से शुरू होकर 3 समकोण घूमे?
(d) 7 से शुरू होकर 2 ऋजुकोण घूमे?
हल:
(a) 6 से शुरू होकर 1 समकोण घूमने पर, घंटे की सुई 9 पर रुक जाती है।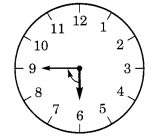

(b) 8 से शुरू होकर 2 समकोण घूमने पर, घंटे की सुई 2 पर रुक जाती है।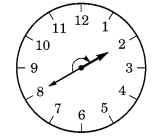

(c) 10 से शुरू होकर 3 समकोण घूमने पर, घंटे की सुई 7 पर रुक जाती है।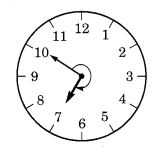

(b) 7 से शुरू होकर 2 समकोण घूमने पर, घंटे की सुई 7 पर रुक जाती है।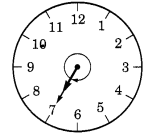

Ex 5.3

प्रश्न 1.
निम्नलिखित का मिलान करें:
(i) सरल कोण (a) एक चक्कर के एक-चौथाई से कम।
(ii) समकोण (b) आधे से अधिक चक्कर।
(iii) न्यून कोण (c) एक चक्कर का आधा।
(iv) अधिक कोण (d) एक चक्कर का एक-चौथाई।
(v) प्रतिवर्ती कोण (e) एक चक्कर के \(\frac { 1 }{ 4 }\) और \(\frac { 1 }{ 2 }\) के बीच। – (f) एक पूर्ण चक्कर।14 and 12 of a revolution.

हल:
(i) सीधा कोण ↔ (c) एक चक्कर का आधा।
(ii) समकोण ↔ (d) एक चक्कर का एक-चौथाई।
(iii) न्यून कोण ↔ (a) एक चक्कर के एक-चौथाई से कम।
(iv) अधिक कोण ↔ (e) एक चक्कर के \(\frac { 1 }{ 4 }\) और \(\frac { 1 }{ 2 }\) के बीच। (v) प्रतिवर्ती कोण ↔ (f) एक पूर्ण चक्कर, समकोण, न्यून, अधिक या प्रतिवर्ती।14 and 12 of a revolution.

प्रश्न 2.
निम्नलिखित कोणों में से प्रत्येक को वर्गीकृत करें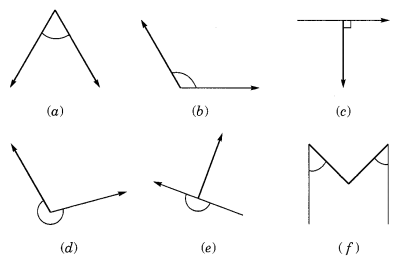

हल:
(a) न्यून कोण
(b) अधिक कोण
(c) समकोण
(d) प्रतिवर्ती कोण
(e) सरल कोण
(f) न्यून कोण

Ex 5.4

प्रश्न 1.
(i) समकोण (ii) ऋजुकोण का माप क्या है?
हल:
(i) समकोण का माप = 90°
(ii) ऋजुकोण का माप = 180°

प्रश्न 2.
सत्य या असत्य बताइए:
(a) 90° से कम न्यून कोण का माप
(b) 90° से कम अधिक कोण का माप
(c) 180° से अधिक प्रतिवर्ती कोण का माप
(d) एक पूर्ण परिक्रमण का माप = 360°
(e) यदि m ∠A = 53° और ∠B = 35° है, तो m∠A > m∠B.
हल:
(a) सत्य
(b) असत्य
(c) सत्य
(d) सत्य
(e) सत्य 

प्रश्न 3.

(a) कुछ न्यून कोण (b) कुछ अधिक कोण
के माप लिखिए । हल: (a) 25°, 63° और 72° न्यून कोण हैं। (b) 105°, 120° और 135° अधिक कोण हैं।

प्रश्न 4.
नीचे दिए गए कोणों को चाँदे की सहायता से मापिए और माप लिखिए।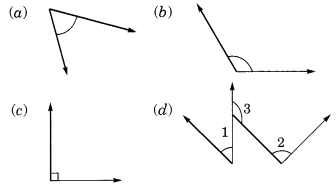

हल:
(a) 45°
(b) 125°
(c) 90°
(d) ∠1 = 60°, ∠2 = 90°, ∠3 = 125°

प्रश्न 5.
किस कोण का माप बड़ा है? पहले अनुमान लगाएँ और फिर मापें।
कोण A का माप =
कोण B का माप =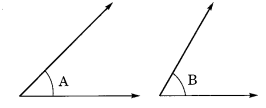

हल:
कोण A का माप = 40°
कोण B का माप = 60°

प्रश्न 6.
इन दोनों कोणों में से किस कोण का माप बड़ा है? अनुमान लगाइए और फिर मापकर पुष्टि कीजिए।
हल:
कोण (b) का उद्घाटन कोण (a) से बड़ा है।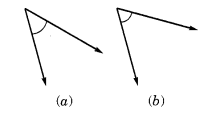

∴ कोण (a) का माप = 45°
और कोण (b) का माप = 60°

प्रश्न 7.
न्यून, अधिक कोण, समकोण या सरल कोण से रिक्त स्थान भरें:
(a) वह कोण जिसका माप समकोण से कम है ………. है।
(b) वह कोण जिसका माप समकोण से अधिक है ………. है।
(c) वह कोण जिसका माप दो समकोणों के मापों का योग है ………. है।
(d) जब दो कोणों के मापों का योग एक समकोण के माप के बराबर होता है, तो उनमें से प्रत्येक ………. होता है।
(e) जब दो कोणों के मापों का योग एक सरल कोण के बराबर होता है और यदि उनमें से एक न्यून कोण है, तो दूसरा ………. होना चाहिए।
हल:
(a) न्यून कोण
(b) अधिक कोण
(c) सरल कोण
(d) न्यून कोण
(e) अधिक कोण

प्रश्न 8.
प्रत्येक आकृति में दर्शाए गए कोण का माप ज्ञात कीजिए। (पहले अपनी आँखों से अनुमान लगाइए और फिर चाँदे की सहायता से वास्तविक माप ज्ञात कीजिए।)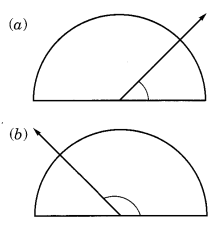
 
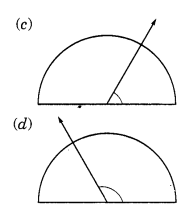
हल:
(a) कोण का माप = 40°
(b) कोण का माप = 130°
(c) कोण का माप = 65°
(d) कोण का माप = 135°

प्रश्न 9.
प्रत्येक आकृति में घड़ी की सुइयों के बीच का कोण ज्ञात कीजिए: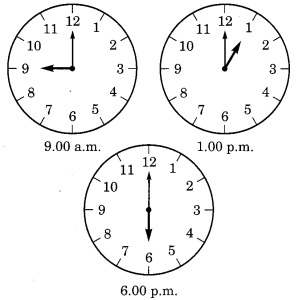

हल:
(i) सुबह 9.00 बजे घड़ी के घंटे की सुई और मिनट की सुई के बीच का कोण = 90°
(ii) दोपहर 1.00 बजे घड़ी के घंटे की सुई और मिनट की सुई के बीच का कोण = 30°
(iii) शाम 6.00 बजे घड़ी के घंटे की सुई और मिनट की सुई के बीच का कोण = 180°।

प्रश्न 10.
जाँच कीजिए: दी गई आकृति में, कोण 30° का है। इसी आकृति को आवर्धक लेंस से देखिए। क्या कोण बड़ा हो जाता है? क्या कोण का आकार बदल जाता है?

हल:
यह एक क्रियाकलाप है। अतः इसे स्वयं करके देखिए।

प्रश्न 11.
प्रत्येक कोण को मापें और वर्गीकृत करें: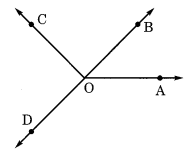

कोण	उपाय	प्रकार
∠एओबी
∠AOC
∠बीओसी
∠DOC
∠DOA
∠जन्मतिथि

समाधान:

कोण	उपाय	प्रकार
∠एओबी	40°	तीव्र कोण
∠AOC	125°	अधिक कोण
∠बीओसी	85°	तीव्र कोण
∠DOC	95°	अधिक कोण
∠DOA	140°	अधिक कोण
∠जन्मतिथि	180°	रेखीय कोण

Ex 5.5

प्रश्न 1.
निम्नलिखित में से कौन लंब रेखाओं के मॉडल हैं:
(a) एक मेज के ऊपरी हिस्से के आसन्न किनारे।
(b) एक रेलवे ट्रैक की रेखाएँ।
(c) एक अक्षर 'L' बनाने वाले रेखाखंड।
(d) अक्षर V।
हल:
(a) हाँ, एक मेज के ऊपरी हिस्से के आसन्न किनारे लंब रेखाओं के मॉडल हैं।
(b) नहीं, एक रेलवे ट्रैक की रेखाएँ एक दूसरे के समानांतर हैं। इसलिए वे लंब रेखाओं के लिए एक मॉडल नहीं हैं।
(c) हाँ, 'L' के दो रेखाखंड लंब रेखाओं के लिए एक मॉडल हैं।
(d) नहीं, 'V' के दो रेखाखंड लंब रेखाओं के लिए एक मॉडल नहीं हैं।

प्रश्न 2.
मान लीजिए \(\overline { PQ }\) रेखाखंड \(\overline { XY }\) पर लंब है। मान लीजिए \(\overline { PQ }\) और \(\overline { XY }\) बिंदु A पर प्रतिच्छेद करते हैं। ∠PAY का माप क्या है? हल: चूँकि \(\overline { PQ }\) ⊥ XY ∴ ∠PAY = 90°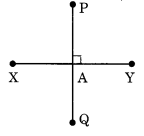PQ¯¯¯¯¯¯¯¯ be the perpendicular to the line segment XY¯¯¯¯¯¯¯¯ . Let PQ¯¯¯¯¯¯¯¯ and XY¯¯¯¯¯¯¯¯ intersect at in the point A. What is the measure of ∠PAY?

PQ¯¯¯¯¯¯¯¯ ⊥ XY

प्रश्न 3.
आपके बॉक्स में दो सेट-स्क्वायर हैं। उनके कोनों पर बनने वाले कोणों के माप क्या हैं? क्या उनमें कोई कोण माप उभयनिष्ठ है?
हल:
दोनों सेट-स्क्वायर के चित्र नीचे दिए गए हैं: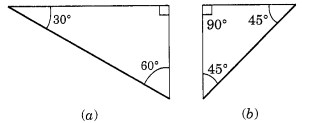

त्रिभुज (a) के माप कोण 30°, 60° और 90° हैं।
त्रिभुज (b) के माप कोण 45°, 45° और 90° हैं।
हाँ, उनका एक उभयनिष्ठ कोण 90° है।

प्रश्न 4.
आरेख का अध्ययन करें। रेखा l, रेखा m पर लंबवत है।
(a) क्या CE = EG है?
(b) क्या PE, CG को समद्विभाजित करता है?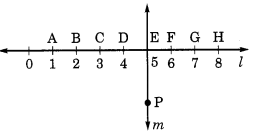

(c) किन्हीं दो रेखाखंडों की पहचान कीजिए जिनके लिए PE लंबवत समद्विभाजक है।
(d) क्या ये सत्य हैं?
(i) AC > FG
(ii) CD = GH
(iii) BC < EH
हल:
(a) हाँ,
क्योंकि, CE = 2 इकाई और EG = 2 इकाई
इसलिए, CE = EG.
(b) हाँ, PE, CG को समद्विभाजित करता है
(c) आवश्यक रेखाखंड जिनके लिए PE लंबवत समद्विभाजक है: \(\overline { BG }\) और \(\overline { DF }\) (d) (i) सत्य (ii) सत्य (iii) सत्यBG¯¯¯¯¯¯¯¯ and DF¯¯¯¯¯¯¯¯

Ex 5.6

प्रश्न 1.
निम्नलिखित त्रिभुजों के प्रकार बताइए:
(a) त्रिभुज जिसकी भुजाओं की लंबाई 7 सेमी, 8 सेमी और 9 सेमी है।
(b) ∆ABC जिसमें AB = 8.7 सेमी, AC = 7 सेमी और BC = 6 सेमी है।
(c) ∆PQR जिससे PQ = QR = PR = 5 सेमी है।
(d) ∆DEF जिसमें m∠D = 90° है।
(e) ∆XYZ जिसमें m∠Y = 90° और XY = YZ है।
(f) ∆LMN जिसमें m∠L = 30° है। m∠M = 70° और m∠N = 80° है।
हल:
(a) एक त्रिभुज की भुजाओं की लंबाई 7 सेमी, 8 सेमी और 9 सेमी दी गई है।
चूँकि, दिए गए त्रिभुज की सभी भुजाएँ अलग-अलग हैं।
इसलिए, यह एक विषमबाहु त्रिभुज है।
(b) दिया गया है: AB = 8.7 सेमी, AC = 7 सेमी तथा BC = 6 सेमी
यहाँ AB ≠ AC ≠ BC अतः, ∆ABC एक विषमकोण त्रिभुज है।
(c) दिया गया है: PQ = QR = PR = 5 सेमी
चूँकि सभी भुजाएँ बराबर हैं।
अतः, यह एक समबाहु त्रिभुज है।
(d) दिया गया है: ∆DEF में, m∠D = 90°
अतः यह एक समकोण त्रिभुज है।
(e) दिया गया है: ∆XYZ में, m∠Y = 90° तथा XY = YZ
अतः यह एक समकोण त्रिभुज है।
(f) दिया गया है: ∆LMN, m∠L = 30°, m∠M = 70° तथा m∠N = 80°
अतः यह एक न्यूनकोण त्रिभुज है।

प्रश्न 2.
निम्नलिखित का मिलान करें:
त्रिभुज का माप त्रिभुज का प्रकार
(i) समान लंबाई की 3 भुजाएँ (a) विषमबाहु
(ii) समान लंबाई की 2 भुजाएँ (b) समद्विबाहु समकोण
(iii) सभी भुजाएँ अलग-अलग लंबाई की हैं (c) अधिक कोण
(iv) 3 न्यून कोण (d) समकोण
(v) 1 समकोण (e) समबाहु
(vi) 1 अधिक कोण (f) न्यून कोण
(vii) समान लंबाई की दो भुजाओं वाला 1 समकोण (g) समद्विबाहु
हल:
(i) ↔ (e)
(ii) ↔ (g)
(iii) ↔
(a)
(iv) ↔ (f) (v) ↔ (d)
(vi) ↔ (c)
(vii) ↔ (b)

प्रश्न 3.
निम्नलिखित त्रिभुजों में से प्रत्येक का दो अलग-अलग तरीकों से नाम लिखिए: (आप अवलोकन द्वारा कोण की प्रकृति का अंदाजा लगा सकते हैं)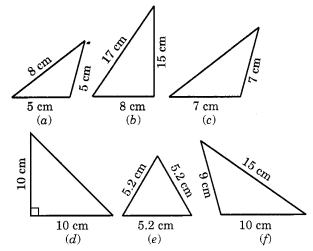

हल:
(a) (i) न्यूनकोण त्रिभुज
(ii) समद्विबाहु त्रिभुज

(b) (i) समकोण त्रिभुज
(ii) विषमबाहु त्रिभुज

(c) (i) अधिककोण त्रिभुज
(ii) समद्विबाहु त्रिभुज

(d) (i) समकोण त्रिभुज
(ii) समद्विबाहु त्रिभुज

(ई) (i) न्यूनकोण त्रिभुज
(ii) समबाहु त्रिभुज

(च) (i) अधिककोण त्रिभुज
(ii) विषमकोण त्रिभुज।

प्रश्न 4.
माचिस की तीलियों का उपयोग करके त्रिभुज बनाने का प्रयास करें। कुछ यहाँ दिखाए गए हैं। क्या आप
(a) 3 माचिस की तीलियों से त्रिभुज बना सकते हैं?
(b) 4 माचिस की तीलियों से?
(c) 5 माचिस की तीलियों से?
(d) 6 माचिस की तीलियों से?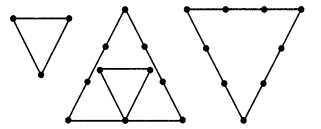

(याद रखें कि आपको प्रत्येक स्थिति में सभी उपलब्ध माचिस की तीलियों का उपयोग करना होगा)
प्रत्येक स्थिति में त्रिभुज के प्रकार का नाम बताइए।
यदि आप त्रिभुज नहीं बना सकते हैं, तो इसके कारण बताइए।
हल:
(a) हाँ, हम 3 माचिस की तीलियों से एक समबाहु त्रिभुज बना सकते हैं।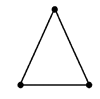

(b) नहीं, हम 4 माचिस की तीलियों से त्रिभुज नहीं बना सकते।
(c) हाँ, हम पाँच माचिस की तीलियों से एक समद्विबाहु त्रिभुज बना सकते हैं।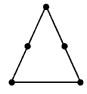

(d) हाँ, हम 6 माचिस की तीलियों से एक समबाहु त्रिभुज बना सकते हैं।

Ex 5.7

प्रश्न 1.
सत्य या असत्य बताइए:
(a) आयत का प्रत्येक कोण समकोण होता है।
(b) आयत की सम्मुख भुजाएँ बराबर लंबाई की होती हैं।
(c) वर्ग के विकर्ण एक दूसरे पर लंबवत होते हैं।
(d) समचतुर्भुज की सभी भुजाएँ बराबर लंबाई की होती हैं।
(e) समांतर चतुर्भुज की सभी भुजाएँ बराबर लंबाई की होती हैं।
(f) समलम्ब चतुर्भुज की सम्मुख भुजाएँ समान्तर होती हैं।
हल:
(a) सत्य
(b) सत्य
(c) सत्य
(d) सत्य
(e) असत्य
(f) असत्य

प्रश्न 2.
निम्नलिखित के लिए कारण दीजिए:
(a) एक वर्ग को एक विशेष आयत माना जा सकता है।
(b) एक आयत को एक विशेष समांतर चतुर्भुज माना जा सकता है।
(c) एक वर्ग को एक विशेष समचतुर्भुज माना जा सकता है।
(d) वर्ग, आयत, समांतर चतुर्भुज सभी चतुर्भुज हैं।
(e) वर्ग एक समांतर चतुर्भुज भी है।
हल:
(a) एक वर्ग में आयत के सभी गुण होते हैं। इसलिए, यह एक विशेष आयत है।
(b) एक आयत में समांतर चतुर्भुज के समान गुण होते हैं। इसलिए, यह एक विशेष समांतर चतुर्भुज है।
(c) एक वर्ग में समचतुर्भुज के समान गुण होते हैं। इसलिए, यह एक विशेष समचतुर्भुज है।
(d) वर्ग, आयत और समांतर चतुर्भुज सभी चतुर्भुज हैं क्योंकि ये सभी चार भुजाओं से घिरे हैं।

प्रश्न 3.
एक आकृति सम चतुर्भुज कहलाती है यदि उसकी भुजाएँ लंबाई में बराबर हों और कोण माप में बराबर हों। क्या आप सम चतुर्भुज की पहचान कर सकते हैं?
हल:
वर्ग ही एकमात्र सम चतुर्भुज है जिसकी भुजाएँ बराबर हों और कोण बराबर हों।
इसलिए, वर्ग एक सम चतुर्भुज है।

Ex 5.8

प्रश्न 1.
जाँच कीजिए कि क्या निम्नलिखित बहुभुज हैं। यदि उनमें से कोई एक बहुभुज नहीं है, तो बताइए क्यों?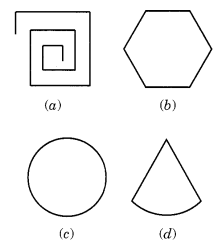

हल:
(a) दी गई आकृति बंद नहीं है। इसलिए, यह बहुभुज नहीं है।
(b) दी गई आकृति एक बहुभुज है।
(c) दी गई आकृति एक बहुभुज नहीं है क्योंकि प्रत्येक बहुभुज रेखाखंडों से घिरा है।
(d) दी गई आकृति एक बहुभुज नहीं है क्योंकि यह एक चाप और दो रेखाखंडों से घिरा है।

प्रश्न 2.
बहुभुज का नाम बताइए।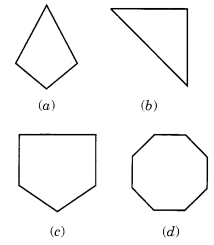

इनमें से प्रत्येक के दो और उदाहरण बनाइए।
हल:
(a) एक चतुर्भुज उदाहरण:

(ख) त्रिभुज
उदाहरण:

(सी) एक पेंटागन
उदाहरण:

(घ) अष्टकोण
उदाहरण:

प्रश्न 3.
एक सम षट्भुज का कच्चा चित्र बनाइए। इसके किन्हीं तीन शीर्षों को जोड़कर एक त्रिभुज बनाइए। आपके द्वारा बनाए गए त्रिभुज का प्रकार पहचानिए।
हल:
ABCDEF एक सम षट्भुज का कच्चा चित्र है। यदि हम किन्हीं तीन शीर्षों जैसे D, A और B को मिलाएँ, तो हमें एक विषमबाहु त्रिभुज DAB प्राप्त होता है।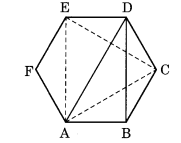

लेकिन यदि हम एकांतर शीर्षों को मिलाएँ, तो हमें एक समबाहु त्रिभुज EAC प्राप्त होता है।

प्रश्न 4.
एक सम अष्टभुज का कच्चा चित्र बनाइए। (यदि आप चाहें तो वर्गाकार कागज़ का प्रयोग कर सकते हैं)। अष्टभुज के ठीक चार शीर्षों को मिलाकर एक आयत बनाइए।
हल:
ABCDEFGH सम अष्टभुज का एक कच्चा चित्र है। GHCD दिए गए अष्टभुज के चारों शीर्षों को मिलाकर बना आयत है।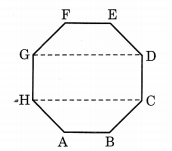

प्रश्न 5.
विकर्ण एक रेखाखंड है जो बहुभुज के किन्हीं दो शीर्षों को मिलाता है और बहुभुज की एक भुजा नहीं है। एक पंचभुज का कच्चा चित्र बनाइए और उसके विकर्ण खींचिए।
हल:
ABCDE एक पंचभुज का कच्चा चित्र है।
इसके किन्हीं दो शीर्षों को मिलाने पर, हमें निम्नलिखित विकर्ण प्राप्त होते हैं:
\(\overline { AD }\) , \(\overline { AC }\) , \(\overline { BE }\) , \(\overline { BD }\) और \(\overline { CE }\)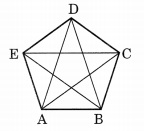AD¯¯¯¯¯¯¯¯ , AC¯¯¯¯¯¯¯¯ , BE¯¯¯¯¯¯¯¯ , BD¯¯¯¯¯¯¯¯ and CE¯¯¯¯¯¯¯¯

Ex 5.9

प्रश्न 1.
निम्नलिखित का मिलान कीजिए: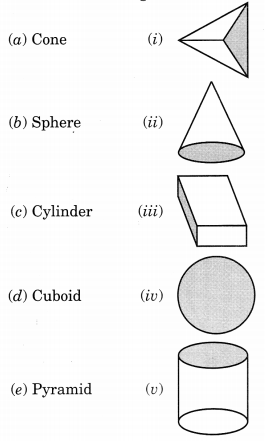

प्रत्येक आकृति के दो उदाहरण दीजिए।
हल:
(a) 4 ↔ (ii)
उदाहरण:
(i) एक आइसक्रीम कोन
(ii) जन्मदिन की टोपी

(b) ↔ (iv)
उदाहरण:
(i) टेनिस बॉल
(ii) क्रिकेट बॉल

(c) ↔ (v)
उदाहरण:
(i) एक रोड रोलर
(ii) एक लॉन रोलर

(d) ↔ (iii)
उदाहरण:
(i) गणित की किताब
(ii) एक ईंट

(e) ↔ (i)
उदाहरण:
(i) हीरा
(ii) मिस्र-पिरामिड

प्रश्न 2. 

(a) आपके उपकरण बॉक्स का आकार क्या है ? 

(b) एक ईंट?

(c) एक माचिस? 

(d) एक रोड-रोलर? 

(e) एक मीठा लड्डू? 

हल: 

(a) उपकरण बॉक्स का आकार घनाभ है। 

(b) एक ईंट का आकार घनाभ है। 

(c) एक माचिस का आकार घनाभ है। 

(d) एक रोड-रोलर का आकार बेलन है।

 (e) एक मीठे लड्डू का आकार गोलाकार है।

InText Questions

लघु उत्तरीय प्रश्न 

प्रश्न 1.
दी गई आकृति में, निम्नलिखित कोणों को न्यून कोण, अधिक कोण, समकोण, सीधा कोण या प्रतिवर्ती कोण के रूप में नाम दें।
(a) ∠QOY
(b) ∠YOP
(c) ∠ROX
(d) ∠QOX
(e) ∠POQ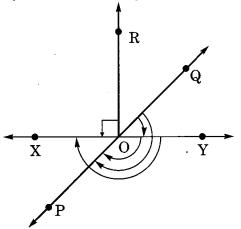

हल:
(a) ∠QOY = न्यून कोण।
(b) ∠YOP = अधिक कोण।
(c) ∠ROX = समकोण।
(d) ∠QOX = प्रतिवर्ती कोण।
(e) ∠POQ = सीधा कोण।

प्रश्न 2.
दी गई आकृति में, a, b, c, d, e और f से अंकित कोणों का माप ज्ञात कीजिए।
हल:
∠a = 180° -129° = 51°
∠b = 180° – (51° + 92°)
= 180° – 143° = 37°
∠c = 180° – 88° = 92°
∠d = 180° – 152° = 28°
∠e = 180° – 143° = 37°
∠f= 180° – (∠e + ∠d)
= 180° – (37° + 28°)
= 180°- 65°= 115°
∠g = 180° – ∠f = 180° – 115° = 65°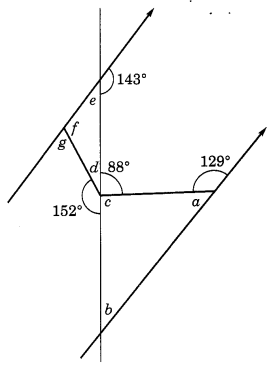

प्रश्न 3.
दिए गए त्रिभुजों को वर्गीकृत कीजिए जिनकी भुजाएँ उन पर अंकित हैं।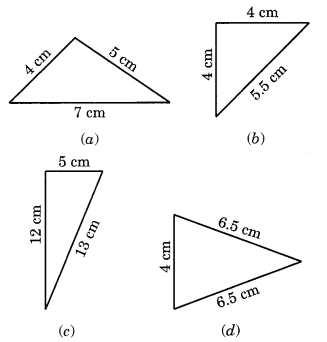

हल:
(a) सभी भुजाएँ भिन्न हैं। अतः यह एक विषमबाहु त्रिभुज है।
(a) त्रिभुज की दो भुजाओं की लंबाइयाँ समान हैं। अतः यह एक समद्विबाहु त्रिभुज है।
(b) सभी भुजाएँ असमान हैं और एक कोण समकोण है। अतः यह एक विषमबाहु समकोण त्रिभुज है।
(c) इस त्रिभुज की दो भुजाएँ बराबर हैं। अतः यह एक समद्विबाहु त्रिभुज है।

प्रश्न 4.
निम्नलिखित में से प्रत्येक को पूरा कीजिए, ताकि एक सत्य कथन बन सके:
(a) ……….. एक आयत है जिसमें आसन्न भुजाओं का एक युग्म बराबर है। (b) समान्तर भुजाओं के एक युग्म वाला समांतर चतुर्भुज ………. कहलाता है। (c) समांतर भुजाओं के ठीक एक युग्म वाला चतुर्भुज ………. कहलाता है। (d) एक चतुर्भुज जिसमें विपरीत भुजाओं के दोनों युग्म समांतर हों, ………. कहलाता है। (e) एक समांतर चतुर्भुज जिसका प्रत्येक कोण समकोण हो, ………. कहलाता है। हल: (a) वर्ग (b) समचतुर्भुज (c) समलंब (d) समांतर चतुर्भुज (e) आयत।

अति लघु उत्तरीय प्रश्न

प्रश्न 1.
निम्नलिखित में से कौन सा रेखाखंड लंबा है?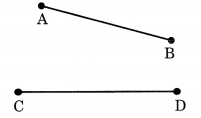

हल:
विभाजक का उपयोग करने पर, CD¯¯¯¯¯¯¯¯ AB¯¯¯¯¯¯¯¯ से लंबा प्रतीत होता है।

प्रश्न 2.
एक त्रिभुज बनाने के लिए कितने रेखाखंडों का उपयोग किया जाता है?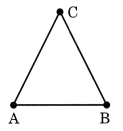

हल:
एक त्रिभुज बनाने के लिए तीन रेखाखंडों का उपयोग किया जाता है।

प्रश्न 3.
ऋजुकोण का माप क्या है?
हल:
ऋजुकोण का माप 180° होता है।

प्रश्न 4.
पूर्ण कोण क्या है?
हल:
एक चक्कर के लिए बने कोण को पूर्ण कोण कहते हैं।

प्रश्न 5.
एक घड़ी की घंटे की सुई द्वारा बनाए गए समकोण की संख्या ज्ञात कीजिए जब यह 3 से 6 पर जाती है।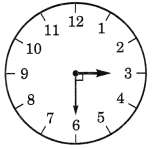

हल:
जब एक घड़ी की घंटे की सुई 3 से 6 पर जाती है, तो यह एक समकोण पर घूमती है।

प्रश्न 6.
निम्नलिखित का रफ चित्र बनाइए:
(a) न्यून कोण
(b) अधिक कोण
(c) प्रतिवर्ती कोण
हल: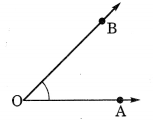

(a) न्यून कोण

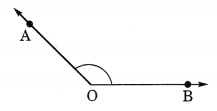
(b) अधिक कोण

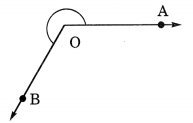
(c) प्रतिवर्त कोण

प्रश्न 7.
दी गई आकृतियों से कोण के प्रकार पहचानें: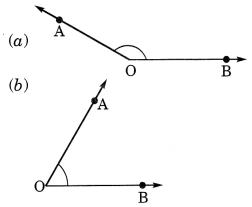


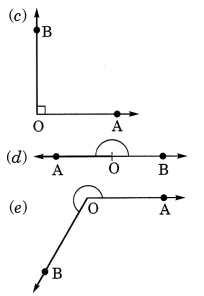
हल:
(a) अधिक कोण
(b) न्यून कोण
(c) समकोण
(d) सरल कोण
(e) प्रतिवर्ती कोण

प्रश्न 8.
निम्नलिखित कोणों के डिग्री माप क्या हैं?
(a) समकोण
(b) पूर्ण कोण
(c) ऋजु कोण
हल:
(a) समकोण का डिग्री माप 90° है।
(b) पूर्ण कोण का डिग्री माप 360° है।
(c) ऋजु कोण का डिग्री माप 180° है।

प्रश्न 9.
कोणों के आधार पर दिए गए त्रिभुज कितने प्रकार के होते हैं?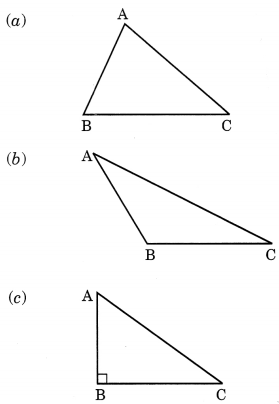

हल:
(a) न्यूनकोण त्रिभुज।
(b) अधिककोण त्रिभुज।
(c) समकोण त्रिभुज।

प्रश्न 10.
भुजाओं के आधार पर निम्नलिखित त्रिभुज कितने प्रकार के होते हैं?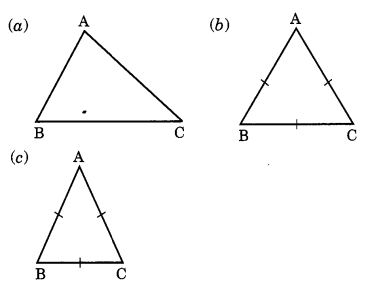

हल:
(a) विषमबाहु त्रिभुज।
(b) समबाहु त्रिभुज।
(c) समद्विबाहु त्रिभुज।

दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
दी गई आकृतियों के लिए 'यूलर के सूत्र' V + F = E + 2 का सत्यापन कीजिए।
(a) एक त्रिभुजाकार प्रिज्म जिसमें 5 फलक, 9 किनारे और 6 शीर्ष हैं।
(b) एक आयताकार प्रिज्म जिसमें 6 फलक, 12 किनारे और 8 शीर्ष हैं।
(c) एक पंचकोणीय प्रिज्म जिसमें 7 फलक, 15 किनारे और 10 शीर्ष हैं।
(d) एक चतुष्फलक - जिसमें 4 फलक, 6 किनारे और 4 शीर्ष हैं।
हल:
(a) यहाँ, F = 5, E = 9 और V = 6
∴ V + F = E + 2
⇒ 6 + 5 = 9 + 2
⇒ 11 = 11
अतः, सत्यापित।

(b) यहाँ, F = 6, E = 12 और V = 8
∴ V + F = E + 2
⇒ 8 + 6 = 12 + 2
⇒ 14 = 14
अतः, सत्यापित।

(c) यहाँ, F = 7, E = 15 और V = 10
∴ V + F = E + 2
⇒ 10 + 7 = 15 + 2
⇒ 17 = 17
अतः, सत्यापित।

(d) यहाँ, F = 4, E = 6 और V = 4
∴ V + F = E + 2
⇒ 4 + 4 = 6 + 2
⇒ 8 = 8
अतः, सत्यापित।

प्रश्न 2.
प्रिज्मों के लिए दी गई तालिका को पूरा करें:

चश्मे	चेहरों की संख्या	किनारों की संख्या	शीर्षों की संख्या
त्रिकोणीय	–	–	–
चतुष्कोष	–	–	–
पंचकोना	–	–	–
षट्कोणीय	–	–	–
अष्टकोन	–	–	–
दस भुजवाला	–	–	–

समाधान:

चश्मे	चेहरों की संख्या	किनारों की संख्या	शीर्षों की संख्या
त्रिकोणीय	5	9	6
चतुष्कोष	6	12	8
पंचकोना	7	15	10
षट्कोणीय	8	18	12
अष्टकोन	10	24	16
दस भुजवाला	12	30	20

बहुविकल्पीय प्रश्न

प्रश्न 1.
एक घड़ी की घंटे की सुई द्वारा घुमाए गए समकोणों की संख्या जब यह 3 से 6 पर जाती है।
(a) 1
(b) 2
(c) 3
(d) 4
समाधान:
सही विकल्प (a) है।

प्रश्न 2.
असमान विपरीत भुजाओं की एक जोड़ी वाले चतुर्भुज को क्या कहते हैं?
(a) समांतर चतुर्भुज
(b) वर्ग
(c) आयत
(d) समलंब चतुर्भुज
हल:
सही विकल्प (d) है।

उच्च क्रम चिंतन कौशल (Hots)

प्रश्न 1.
दी गई आकृति में, x, y, z, s और m के मान ज्ञात कीजिए।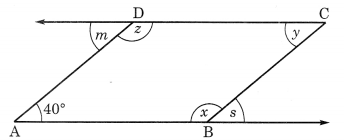

हल:
दिया गया है कि ∠A = 40°
(i) ∠DAB + ∠ABC = 180° (आसन्न कोण)
⇒ 40° + ∠ABC = 180°
⇒ ∠ABC = 180° – 40° = 140°
अतः, ∠x = 140°

(ii) ∠x + ∠y = 180° (आसन्न कोण)
⇒ 140° + ∠y = 180°
⇒ ∠y = 180° – 140° = 40°
अतः, ∠y = 40°

(iii) ∠y + ∠z – 180° (आसन्न कोण)
⇒ 40° + ∠z = 180°
⇒ ∠z = 180° – 40° = 140°
अतः, ∠z = 140°

(iv) ∠x + ∠s = 180° (सीधे कोण)
⇒ 140° + ∠s = 180°
⇒ ∠s = 180° – 140° = 40°
अतः, ∠s = 40°

(v) ∠m + ∠z = 180° (सीधे कोण)
⇒ ∠m + 140° = 180°
⇒ ∠m = 180° – 140° = 40°

प्रश्न 2.
दी गई आकृति से x का मान ज्ञात कीजिए और त्रिभुज के प्रत्येक कोण का माप ज्ञात कीजिए।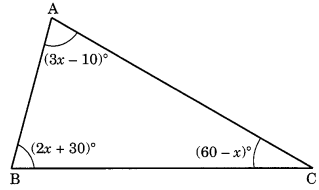

हल:
(i) त्रिभुज के तीन कोणों का योग = 180°
∴ 2x + 30° + 60° – x + 3x – 10° = 180°
⇒ (2x – x + 3x) + (30° + 60° – 10°) = 180°
⇒ 4x + 80° = 180°
⇒ 4x = 180° – 80°
⇒ 4x = 100°
∴ x = 10004 = 25°
∴ कोणों के माप हैं:
(i) (2x + 30)° – 2 x 25° + 30° = 80°
(ii) (60 – x)° = 60° – 25° = 35°
(iii) (3x – 10)° = 3 x 25° – 10° = 75° – 10° = 65°
अतः, x = 25° और त्रिभुजों के कोण हैं: 80°, 35° और 65°।