SikhLo - Current Affairs in Hindi, Daily current affairs, Current affairs

 NCERT Class 7 Maths Chapter 10 प्रायोगिक ज्यामिति

NCERT Solutions for Class 7 Maths Chapter 10 प्रायोगिक ज्यामिति

Ex 10.1

प्रश्न 1.
एक रेखा, मान लीजिए AB, खींचिए और उसके बाहर एक बिंदु C लीजिए। C से होकर, केवल रूलर और परकार की सहायता से AB के समांतर एक रेखा खींचिए।
हल:
रचना के चरण

1. एक रेखा AB खींचिए।
2. इसके बाहर एक बिंदु C लीजिए।
3. AB पर कोई बिंदु D लीजिए।
4. C को D से मिलाइये।
   
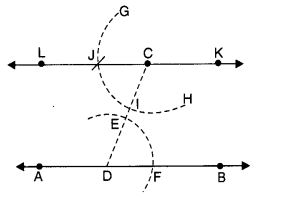
5. D को केंद्र मानकर तथा सुविधाजनक त्रिज्या लेकर AB को F पर तथा CD को E पर काटते हुए एक चाप खींचा।
6. अब C को केंद्र मानकर तथा चरण 5 के समान त्रिज्या लेकर, CD को I पर काटते हुए एक चाप GH खींचिए।
7. कम्पास की नुकीली नोक को F पर रखें और छिद्र को इस प्रकार समायोजित करें कि पेंसिल की नोक E पर हो।
8. चरण 7 के समान खुले स्थान पर तथा I को केंद्र मानकर, चाप GH को J पर काटते हुए एक चाप खींचिए।
9. अब CJ को मिलाकर एक रेखा 'KL' खींचिए। तब KL अभीष्ट रेखा है।

प्रश्न 2.
एक रेखा l खींचिए। l पर स्थित किसी भी बिंदु पर l पर एक लंब खींचिए। इस लंब पर l से 4 सेमी दूर एक बिंदु X लीजिए। X से होकर l के समांतर एक रेखा m खींचिए।
हल:
रचना के चरण

1. एक रेखा l खींचिए।
2. रेखा l पर कोई भी बिंदु A लीजिए।
   
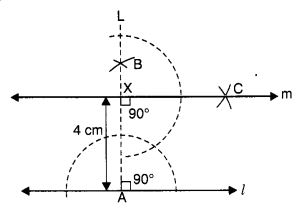
3. रेखा l के बिन्दु A पर 90° का कोण बनाइए और रेखा l पर लंबवत रेखा AL खींचिए।
4. AL पर एक बिन्दु X इस प्रकार अंकित करें कि AX = 4 सेमी.
5. X पर 90° का कोण बनाइये और रेखा AL के लंबवत एक रेखा XC खींचिए।
6. तब रेखा XC (रेखा m) X से होकर जाने वाली अपेक्षित रेखा है जैसे कि m || l.

प्रश्न 3.
मान लीजिए l एक रेखा है और P एक बिंदु है जो l पर नहीं है। P से होकर l के समांतर एक रेखा m खींचिए। अब P को l पर स्थित किसी बिंदु Q से मिलाइए। m पर कोई अन्य बिंदु R चुनिए। R से होकर PQ के समांतर एक रेखा खींचिए। मान लीजिए यह l को S पर मिलती है। समांतर रेखाओं के ये दो समूह किस आकृति को वृत्ताकार बनाते हैं?
हल:
रचना के चरण

1. एक रेखा l खींचिए और उस पर न स्थित एक बिंदु P लीजिए।
2. l पर कोई भी बिंदु Q लीजिए।
3. Q को P से मिलाइये।
   
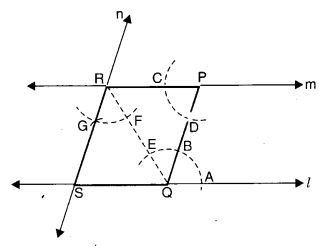
4. रेखा l के समांतर एक रेखा m खींचिए, जैसा कि चित्र में दिखाया गया है। फिर रेखा m || रेखा l को रेखा m बनाएँ।
5. P को l पर किसी भी बिंदु Q से मिलाइये।
6. m पर कोई भी बिंदु R चुनें।
7. R को Q से मिलाइये।
8. R से होकर रेखा PQ के समान्तर एक रेखा n खींचिए।
9. मान लीजिए रेखा n, रेखा l से S पर मिलती है।
10. तब, समान्तर रेखाओं के दो समुच्चयों से घिरा आकार एक समान्तर चतुर्भुज होता है।

Ex 10.2

प्रश्न 1.
एक XYZ की रचना कीजिए जिसमें XY = 4.5 सेमी, YZ = 5 सेमी और ZX = 6 सेमी हो।
हल:
रचना के चरण

1. 5 सेमी लम्बाई का एक रेखाखंड YZ खींचिए।
   
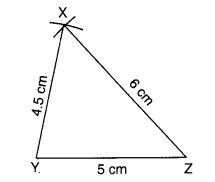
2. Y को केंद्र मानकर 4.5 सेमी त्रिज्या का चाप खींचिए।
3. Z को केंद्र मानकर 6 सेमी त्रिज्या का चाप खींचिए।
4. चापों के प्रतिच्छेद बिंदु को X से चिह्नित करें।
5. XY और XZ को मिलाइए। ∆ XYZ अब तैयार है।

प्रश्न 2.
5.5 सेमी भुजा वाला एक समबाहु त्रिभुज बनाइए।
हल:
रचना के चरण:

1. 5.5 सेमी लम्बाई का एक रेखाखंड BC खींचिए।
2. B को केन्द्र मानकर 5.5 सेमी त्रिज्या का चाप खींचिए।
   
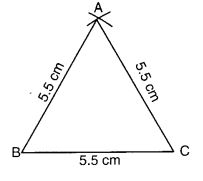
3. C को केन्द्र मानकर 5.5 सेमी त्रिज्या का चाप खींचिए।
4. चापों के प्रतिच्छेद बिन्दु को A से चिह्नित करें।
5. AB और AC को मिलाइए। अब समबाहु ∆ ABC तैयार है।

प्रश्न 3.
PQ = 4 सेमी, QR = 3.5 सेमी और PR = 4 सेमी लेकर ∆ PQR की रचना कीजिए। यह किस प्रकार का त्रिभुज है?
हल:
रचना के चरण:

1. 3.5 सेमी लम्बाई का एक रेखाखंड QR खींचिए।
2. Q को केन्द्र मानकर 4 सेमी त्रिज्या का चाप खींचिए।
3. R को केन्द्र मानकर 4 सेमी त्रिज्या का चाप खींचिए।
   
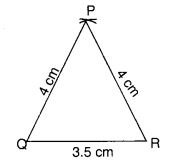
4. चापों के प्रतिच्छेद बिन्दु को P से चिह्नित करें।
5. PQ और PR को मिलाइये।

∆ PQR अब तैयार है,
∵ PQ = PR
∴ ∆ PQR समद्विबाहु है।

प्रश्न 4.
∆ ABC की रचना इस प्रकार कीजिए कि AB = 2.5 सेमी, BC = 6 सेमी और AC = 6.5 सेमी हो। ∠B मापिए।
हल:
रचना के चरण

1. 6 सेमी लम्बाई का एक रेखाखंड BC खींचिए।
   
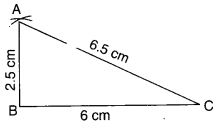
2. B को केन्द्र मानकर 2.5 सेमी त्रिज्या का चाप खींचिए।
3. C को केंद्र मानकर 6.5 सेमी त्रिज्या का चाप खींचिए।
4. चापों के प्रतिच्छेद बिन्दु को A से चिह्नित करें।
5. AB और AC को मिलाइये।
6. ∆ ABC अब तैयार है। मापने पर, ∠B = 90° है।

Ex 10.3

प्रश्न 1.
ADEF की रचना इस प्रकार कीजिए कि DE = 5 सेमी, DF 3 सेमी, तथा m ∠EDF = 90° हो।
हल:
रचना के चरण: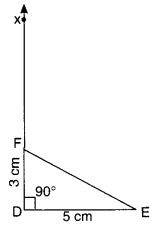

1. एक रेखाखंड DE = 5 सेमी खींचिए।
2. ∠EDX = 90° खींचिए।
3. केंद्र D और त्रिज्या = 3 सेमी लेकर, DX को F पर प्रतिच्छेद करने के लिए एक चाप लगाएं।
4. EF को मिलाकर अभीष्ट त्रिभुज DBF प्राप्त कीजिए।

प्रश्न 2.
एक समद्विबाहु त्रिभुज की रचना कीजिए जिसकी प्रत्येक समान भुजा की लंबाई 6.5 सेमी हो और उनके बीच का कोण 110° हो।
हल:
रचना के चरण

1. 6.5 सेमी लम्बाई का एक रेखाखंड QR खींचिए।
2. Q पर, चाँदे का उपयोग करके QR के साथ 110° बनाते हुए QX खींचें।
   
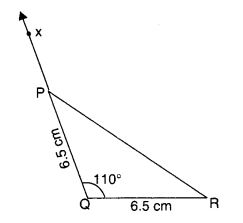
3. बिन्दु Q को केन्द्र मानकर 6.5 सेमी त्रिज्या का चाप लगाया जो QX को P पर काटता है।
4. PR को मिलाइए। अब ∆ PQR प्राप्त होगा।

प्रश्न 3.
BC = 7.5 सेमी, AC = 5 सेमी और m ∠C = 60° लेकर ∆ ABC की रचना कीजिए।
हल:
रचना के चरण: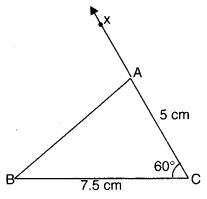

1. एक रेखाखण्ड BC = 7.5 सेमी खींचिए।
2. ∠BCX = 60° खींचिए।
3. C को केंद्र मानकर तथा त्रिज्या = 5 सेमी लेकर एक चाप खींचिए जो CX को A पर काटता है।
4. AB को मिलाकर अभीष्ट ∆ABC प्राप्त कीजिए।

Ex 10.4

प्रश्न 1.
त्रिभुज ABC की रचना कीजिए, जिसमें m ∠A = 60°, m ∠B = 30° और AB = 5.8 सेमी दिया गया है।
हल:
रचना के चरण

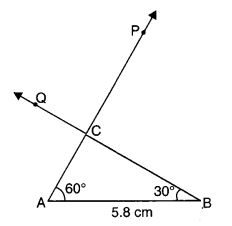
1. 5.8 सेमी लम्बाई का AB खींचिए।
2. बिंदु A पर AB से 60° का कोण बनाते हुए एक किरण AP खींचिए।
3. बिंदु B पर BA से 30° का कोण बनाते हुए एक किरण BQ खींचिए।
4. दो किरणों के प्रतिच्छेद बिन्दु को C से चिह्नित करें।
5. ∆ ABC अब पूर्ण हो गया है।

प्रश्न 2.
त्रिभुज PQR की रचना कीजिए यदि PQ = 5 सेमी, m ∠PQR = 105° तथा m ∠QRP = 40° हो।
(संकेत: त्रिभुज के कोण-योग गुण को याद कीजिए)।
हल:
त्रिभुज के कोण-योग गुण से
m ∠RPQ + m ∠PQR + m ∠QRP = 180°
⇒ m ∠RPQ + 105° + 40° = 180°
⇒ m ∠RPQ + 145° = 180°
⇒ m ∠RPQ = 35°
रचना के चरण

1. 5 सेमी लम्बाई का एक रेखाखंड PQ खींचिए।
2. बिंदु Q पर QP से 105° का कोण बनाते हुए एक किरण QX खींचिए।
   
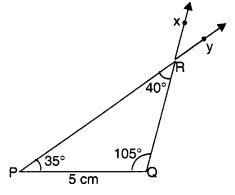
3. P पर PQ से 35° का कोण बनाते हुए एक किरण PY खींचिए।
4. दो किरणों के प्रतिच्छेद बिन्दु को R से चिह्नित करें।

∆ PQR अब पूरा हो गया है।

प्रश्न 3.
जाँच कीजिए कि क्या आप ∆DEF की रचना इस प्रकार कर सकते हैं कि EF = 7.2 सेमी, m ∠E = 110° और m ∠F = 80° हो। अपने उत्तर का औचित्य सिद्ध कीजिए।
हल:
m ∠E + m ∠F = 110° + 80° = 190° > 180°
यह संभव नहीं है क्योंकि त्रिभुज के तीनों कोणों के मापों का योग 180° होता है। अतः, त्रिभुज के दो कोणों का योग 180° से अधिक नहीं हो सकता।
अतः, ∆DEF की रचना नहीं की जा सकती।

Ex 10.5

प्रश्न 1.
समकोण ∆ PQR की रचना कीजिए, जहाँ m ∠Q = 90°, QR = 8 सेमी और PR = 10 सेमी है।
हल:
रचना के चरण:

1. 8 सेमी लम्बाई का QR बनाइये।
   
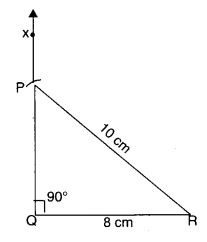
2. Q पर QX ⊥ QR खींचिए।
3. R को केन्द्र मानकर 10 सेमी त्रिज्या का चाप खींचिए।
4. इन दोनों के मिलन बिंदु को P से चिह्नित करें।

अब ∆ PQR प्राप्त होता है।

प्रश्न 2.
एक समकोण त्रिभुज की रचना कीजिए जिसका कर्ण 6 सेमी लंबा है और एक भुजा 4 सेमी लंबी है।
हल:
रचना के चरण

1. 4 सेमी लम्बाई का QR बनाइये।
2. Q पर QX ⊥ QR खींचिए।
   
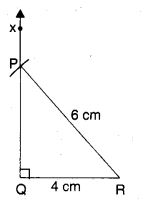
3. R को केन्द्र मानकर 6 सेमी त्रिज्या का चाप खींचिए।
4. चाप और QX के मिलन बिंदु को P से चिह्नित करें।

अब ∆ PQR प्राप्त होता है।

प्रश्न 3.
एक समद्विबाहु समकोण त्रिभुज ABC की रचना कीजिए, जहाँ m ∠ACB = 90° और AC = 6 सेमी है।
हल:
रचना के चरण

1. 6 सेमी लम्बाई का AC खींचिए।
2. C पर CX ⊥ CA खींचिए।
   
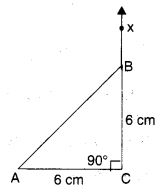
3. C को केन्द्र मानकर 6 सेमी त्रिज्या का चाप खींचिए जो CX को B पर प्रतिच्छेदित करता है।
4. AB को मिलाइए। अब ∆ACB प्राप्त होता है।