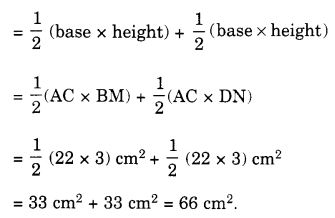NCERT Class 7 Maths Chapter 11 परिमाप और क्षेत्रफल

 NCERT Class 7 Maths Chapter 11 परिमाप और क्षेत्रफल

NCERT Solutions for Class 7 Maths Chapter 11 परिमाप और क्षेत्रफल

Ex 11.1

प्रश्न 1.
एक आयताकार भूमि के टुकड़े की लंबाई और चौड़ाई क्रमशः 500 मीटर और 300 मीटर है।
(i) इसका क्षेत्रफल
(ii) भूमि की कीमत ज्ञात कीजिए, यदि 1 मीटर 2 भूमि की कीमत ₹ 10,000 है।
हल: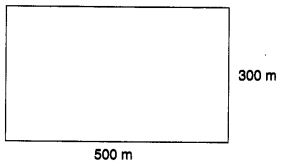

यहाँ, लंबाई = 500 मीटर, चौड़ाई = 300 मीटर
(i) क्षेत्रफल = लंबाई × चौड़ाई = (500 × 300) मीटर 2 = 1,50,000 मीटर 2 (ii) ₹ 10,000 प्रति 1 मीटर
2 की दर से भूमि की कीमत= ₹ (10,000 × 1,50,000) = ₹ 1,50,00,00,000

प्रश्न 2.
एक वर्गाकार पार्क का क्षेत्रफल ज्ञात कीजिए जिसका परिमाप 320 मीटर है।
हल:

प्रश्न 3.
एक आयताकार भूखंड की चौड़ाई ज्ञात कीजिए, यदि उसका क्षेत्रफल 440 वर्ग मीटर और लंबाई 22 मीटर है। साथ ही, उसका परिमाप भी ज्ञात कीजिए।
हल: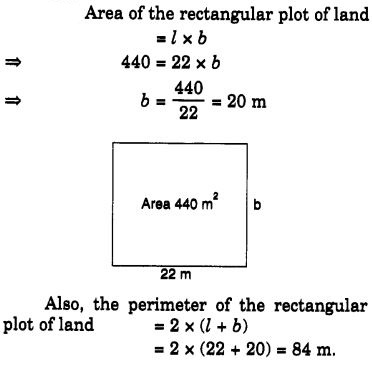

प्रश्न 4.
एक आयताकार शीट का परिमाप 100 सेमी है। यदि लंबाई 35 सेमी है, तो इसकी चौड़ाई ज्ञात कीजिए। क्षेत्रफल भी ज्ञात कीजिए।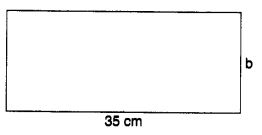

हल:

प्रश्न 5.
एक वर्गाकार पार्क का क्षेत्रफल एक आयताकार पार्क के क्षेत्रफल के बराबर है। यदि वर्गाकार पार्क की भुजा 60 मीटर है और आयताकार पार्क की लंबाई 90 मीटर है, तो आयताकार पार्क की चौड़ाई ज्ञात कीजिए।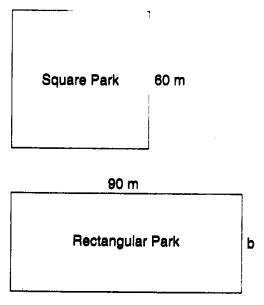

हल:


अतः, आयताकार पार्क की चौड़ाई 40 मीटर है।

प्रश्न 6.
एक तार आयत के आकार का है। इसकी लंबाई 40 सेमी और चौड़ाई 22 सेमी है। यदि इसी तार को पुनः एक वर्ग के आकार में मोड़ा जाए, तो प्रत्येक भुजा का माप क्या होगा? साथ ही, यह भी बताइए कि कौन सी आकृति अधिक क्षेत्रफल घेरती है?
हल:

प्रश्न 7.
एक आयत का परिमाप 130 सेमी है। यदि आयत की चौड़ाई 30 सेमी है, तो उसकी लंबाई ज्ञात कीजिए। आयत का क्षेत्रफल भी ज्ञात कीजिए।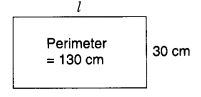

हल: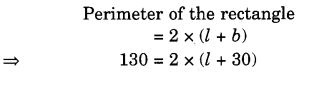

प्रश्न 8.
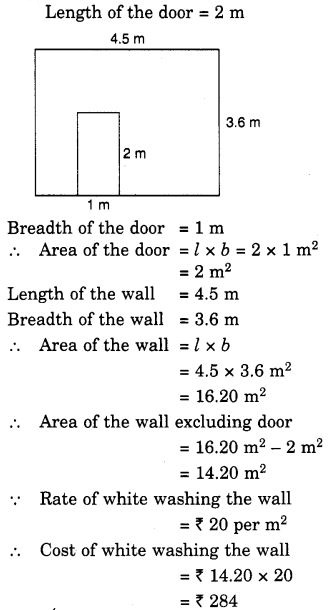
एक दीवार में 2 मीटर लंबा और 1 मीटर चौड़ा एक दरवाजा लगा है। दीवार की लंबाई 4.5 मीटर और चौड़ाई 3.6 मीटर है (चित्र)। दीवार पर सफेदी कराने की लागत ज्ञात कीजिए, यदि दीवार पर सफेदी कराने की दर ₹20 प्रति वर्ग मीटर है । हल
:

Ex 11.2

प्रश्न 1.
निम्नलिखित समांतर चतुर्भुजों का क्षेत्रफल ज्ञात कीजिए: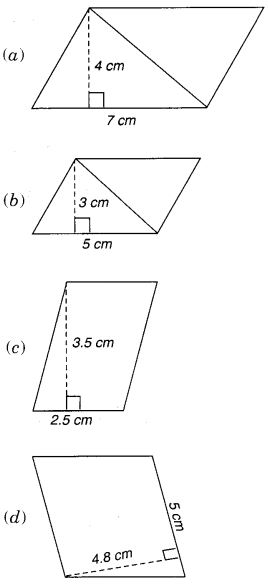


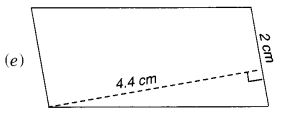
हल:

प्रश्न 2.
निम्नलिखित त्रिभुजों में से प्रत्येक का क्षेत्रफल ज्ञात कीजिए: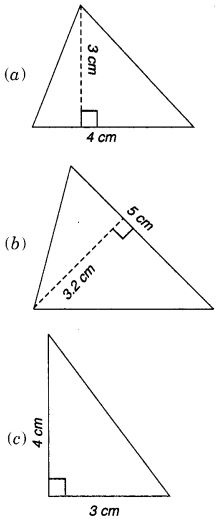


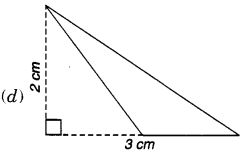
हल:

प्रश्न 3.
लुप्त मान ज्ञात कीजिए: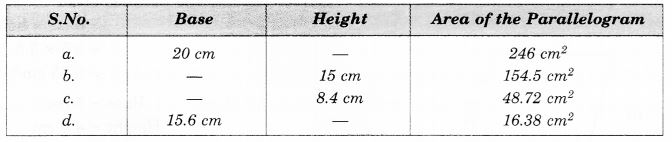

हल: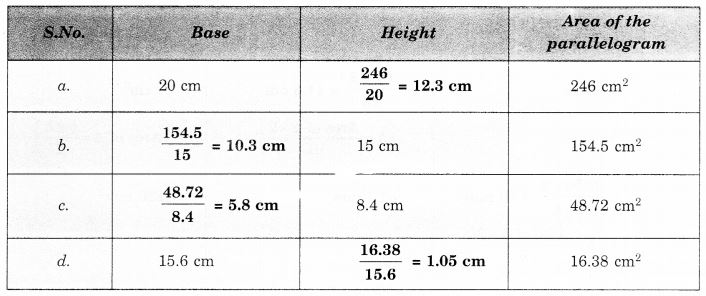

प्रश्न 4.
लुप्त मान ज्ञात कीजिए: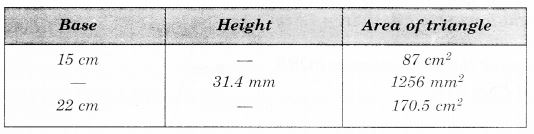

हल:

प्रश्न 5.
PQRS एक समांतर चतुर्भुज है (चित्र में)। QM, Q से SR तक की ऊँचाई है और QN, Q से PS तक की ऊँचाई है। यदि SR = 12 सेमी और QM = 7.6 सेमी। ज्ञात कीजिए:
(a) समांतर चतुर्भुज PQRS का क्षेत्रफल
(b) QN, यदि PS = 8 सेमी।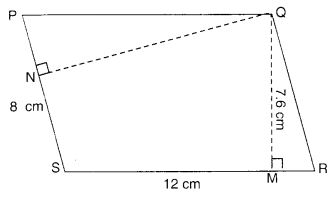

हल:
(a) समांतर चतुर्भुज PQRS का क्षेत्रफल = आधार × ऊँचाई = SR × QM = 12 × 7.6 सेमी 2 = 91.2 सेमी 2
(b) समांतर चतुर्भुज PQRS का क्षेत्रफल = आधार × ऊँचाई = PS × QN
⇒ 91.2 = 8 × QN
⇒ QN = 9128 सेमी
⇒ QN = 11.4 सेमी।

प्रश्न 6.
DL और BM क्रमशः समांतर चतुर्भुज ABCD (चित्र में) की भुजाओं AB और AD की ऊँचाइयाँ हैं। यदि एक समांतर चतुर्भुज का क्षेत्रफल 1470 वर्ग सेमी है, AB = 35 सेमी और AD = 49 सेमी है, तो BM और DL की लंबाई ज्ञात कीजिए।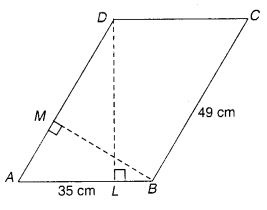

हल:

प्रश्न 7.
∆ ABC, A पर समकोण है (चित्र में)। AD, BC पर लंबवत है। यदि AB = 5 सेमी, BC = 13 सेमी और AC = 12 सेमी है, तो ∆ ABC का क्षेत्रफल ज्ञात कीजिए। AD की लंबाई भी ज्ञात कीजिए।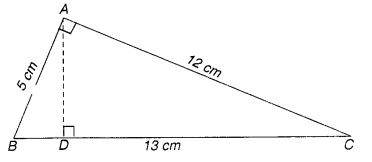

हल:

प्रश्न 8.
∆ ABC समद्विबाहु है जिसमें AB = AC = 7.5 सेमी, और BC = 9 सेमी (चित्र में)। A से BC तक AD की ऊँचाई 6 सेमी है। ∆ ABC का क्षेत्रफल ज्ञात कीजिए। C से AB अर्थात् CE तक की ऊँचाई क्या होगी?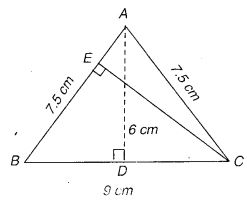

हल:

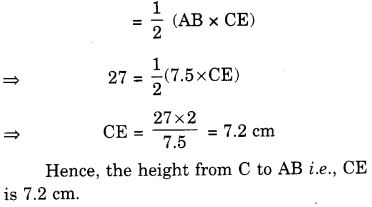
Ex 11.3

प्रश्न 1.
निम्नलिखित त्रिज्या वाले वृत्तों की परिधि ज्ञात कीजिए (π = 227 लीजिए)
(a) 14 सेमी
(b) 28 मिमी
(c) 21 सेमी
हल:

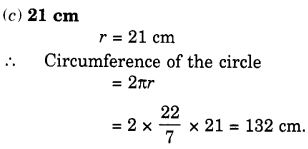
प्रश्न 2.
निम्नलिखित वृत्तों का क्षेत्रफल ज्ञात कीजिए, दिया गया है: ( लीजिए π = 227 )
(a) त्रिज्या = 14 मिमी
(b) व्यास = 49 मीटर
(c) त्रिज्या = 5 सेमी.
हल:

प्रश्न 3.
यदि एक वृत्ताकार शीट की परिधि 154 मीटर है, तो इसकी त्रिज्या ज्ञात कीजिए। शीट का क्षेत्रफल भी ज्ञात कीजिए। (π = 227 लीजिए।)
हल:
वृत्ताकार शीट की परिधि = 154 मीटर।
मान लीजिए वृत्ताकार शीट की त्रिज्या r सेमी है
, तो इसकी परिधि = 2nr मीटर। प्रश्न के अनुसार,
परिधि = 2πr = 154

प्रश्न 4.
एक माली 21 मीटर व्यास वाले एक वृत्ताकार बगीचे की बाड़ लगाना चाहता है। यदि वह दो बार बाड़ लगाता है, तो उसे कितनी लंबाई की रस्सी खरीदनी पड़ेगी? यदि रस्सी की कीमत ₹4 प्रति मीटर है, तो उसकी कीमत भी ज्ञात कीजिए। ( π = 227 लें)
हल:
वृत्ताकार बगीचे का व्यास (r) = 21 मीटर
वृत्ताकार बगीचे की त्रिज्या (r) = 212 मीटर
∴ वृत्ताकार बगीचे की परिधि = 2πr
= 2 × 227 × 212 मीटर = 66 मीटर
⇒ बाड़ का 1 चक्कर लगाने के लिए आवश्यक रस्सी की लंबाई = 66 मीटर
⇒ बाड़ के 2 चक्कर लगाने के लिए आवश्यक रस्सी की लंबाई
= 66 × 2 मीटर = 132 मीटर
प्रति मीटर रस्सी की कीमत = ₹ 4
∴ रस्सी की कीमत = ₹ 132 × 4 = ₹ 528.

प्रश्न 5.
4 सेमी त्रिज्या वाली एक वृत्ताकार शीट में से 3 सेमी त्रिज्या वाला एक वृत्त हटा दिया जाता है। शेष शीट का क्षेत्रफल ज्ञात कीजिए। (π = 3.14 लीजिए)
हल:

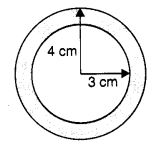
यहाँ, बाहरी त्रिज्या, r = 4 सेमी
आंतरिक त्रिज्या, r = 3 सेमी
शेष शीट का क्षेत्रफल = बाहरी क्षेत्रफल - आंतरिक क्षेत्रफल =
π (R 2 - r 2 ) = 3.14 (4 2 - 3 2 ) सेमी 2
= 3.14 (16 - 9) सेमी 2
= 3.14 × 7 सेमी 2 = 21.98 सेमी 2

प्रश्न 6.
साइमा 1.5 मीटर व्यास वाले एक वृत्ताकार टेबल कवर के किनारे पर फीता लगाना चाहती है। आवश्यक फीते की लंबाई ज्ञात कीजिए और यदि एक मीटर फीते की कीमत ₹ 15 है तो इसकी कीमत भी ज्ञात कीजिए। (π = 3.14 लीजिए)
हल:
टेबल कवर का व्यास = 1.5 मीटर
⇒ टेबल कवर की त्रिज्या (r) = \(\frac { 1.5 }{ 2 } \) मीटर ⇒ टेबल कवर की परिधि = 2πr = 2 × 3.14 × \(\frac { 1.5 }{ 2 } \) मीटर = 4.71 मीटर ⇒ आवश्यक फीते की लंबाई = 4.71 मीटर ∵ प्रति मीटर फीते की कीमत = ₹ 15 ∴ फीते की कीमत = ₹ 4.71 × 15 = ₹ 70.651.52 m

1.52 m = 4.71 m

प्रश्न 7.
निम्नलिखित आकृति का परिमाप ज्ञात कीजिए, जो अपने व्यास सहित एक अर्धवृत्त है।

प्रश्न 8.
1.6 मीटर व्यास वाले एक वृत्ताकार टेबल-टॉप को पॉलिश करने की लागत ज्ञात कीजिए, यदि पॉलिश करने की दर ₹ 15/मी 2 है । (π = 3.14 लें)
हल:
टेबल-टॉप का व्यास = 1.6 मीटर
⇒ टेबल-टॉप की त्रिज्या (r) = \(\frac { 1.6 }{ 2 } \) मीटर = 0.8 मीटर ∴ टेबल-टॉप का क्षेत्रफल = πr 2 = 3.14 × (0.8)2 मीटर 2 = 3.14 × 0.64 मीटर 2 = 2.0096 मीटर 2 ∵ पॉलिश करने की दर = ₹ 15 प्रति मीटर 2 ∴ टेबल-टॉप को पॉलिश करने की लागत = ₹ 2.0096 × 15 = ₹ 30.144 = ₹ 30.14 (लगभग)।1.62 m = 0.8 m

प्रश्न 9.
शाज़ली ने 44 सेमी लंबा एक तार लिया और उसे एक वृत्त के आकार में मोड़ दिया। उस वृत्त की त्रिज्या ज्ञात कीजिए। उसका क्षेत्रफल भी ज्ञात कीजिए। यदि उसी तार को एक वर्ग के आकार में मोड़ा जाए, तो उसकी प्रत्येक भुजा की लंबाई क्या होगी? कौन सी आकृति अधिक क्षेत्रफल घेरती है, वृत्त या वर्ग? (π = \(\frac { 22 }{ 7 } \) लीजिए227 )
हल:

प्रश्न 10.
14 सेमी त्रिज्या वाली एक वृत्ताकार कार्ड शीट से, 3.5 सेमी त्रिज्या वाले दो वृत्त और 3 सेमी लंबाई तथा 1 सेमी चौड़ाई वाला एक आयत निकाल दिया जाता है (जैसा कि आकृति में दर्शाया गया है)। शेष 22
शीट का क्षेत्रफल ज्ञात कीजिए। (π = \(\frac { 22 }{ 7 }\) लें) उत्तर: गोलाकार कार्ड शीट की त्रिज्या =14 सेमी शीट का क्षेत्रफल = πr 2 वर्ग मीटर = \(\frac { 22 }{ 7 }\) × 14 × 14 सेमी 2 = 22 × 2 × 14 सेमी2 = 616 सेमी 2 एक छोटे वृत्त की त्रिज्या = 3.5 सेमी 2 छोटे वृत्तों का क्षेत्रफल = 2 × πr 2 वर्ग मीटर = 2 × \(\frac { 22 }{ 7 }\) × 3.5 × 3.5 सेमी 2 = 2 × 22 × 0.5 × 3.5 सेमी = 77 सेमी 2 एक छोटे आयत की लंबाई = 3 सेमी एक छोटे आयत की चौड़ाई = 1 सेमी। छोटे आयत का क्षेत्रफल = l × b वर्ग मीटर = 3 × 1 सेमी 2 = 3 सेमी 2 शेष शीट का क्षेत्रफल = वृत्ताकार शीट का क्षेत्रफल - (दो छोटे वृत्तों का क्षेत्रफल + आयत का क्षेत्रफल) = 616 सेमी 2 - (77 + 3) सेमी 2 = 616 सेमी 2 - 80 सेमी 2 = 536 सेमी 2 ∴ शेष शीट का अभीष्ट क्षेत्रफल = 536 सेमी 2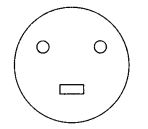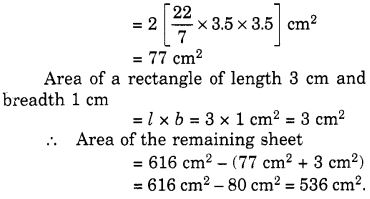227)

प्रश्न 11.
6 सेमी भुजा वाली एक एल्युमीनियम शीट के वर्गाकार टुकड़े से 2 सेमी त्रिज्या का एक वृत्त काटा जाता है। बची हुई एल्युमीनियम शीट का क्षेत्रफल क्या है? (π = 3.14 लीजिए)
हल: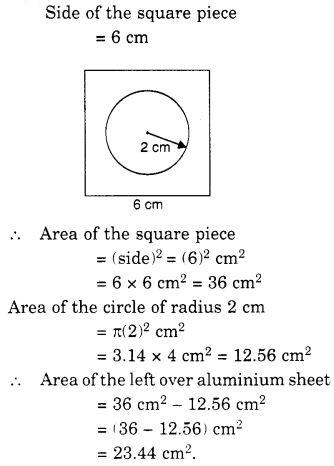

प्रश्न 12.
एक वृत्त की परिधि 31.4 सेमी है। वृत्त की त्रिज्या और क्षेत्रफल ज्ञात कीजिए? (π = 3.14 लीजिए)
हल:

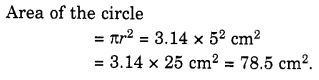
प्रश्न 13.
एक वृत्ताकार फूलों की क्यारी 4 मीटर चौड़े पथ से घिरी हुई है। फूलों की क्यारी का व्यास 66 मीटर है। इस पथ का क्षेत्रफल क्या है? (π = 3.14)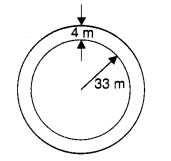

हल: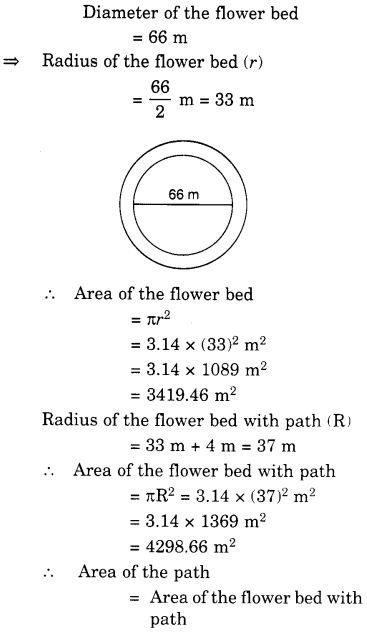

प्रश्न 14.
एक गोलाकार फूलों के बगीचे का क्षेत्रफल लगभग 314 मी 2 है । बगीचे के केंद्र में लगा एक स्प्रिंकलर 12 मी त्रिज्या वाले क्षेत्र को कवर कर सकता है। क्या स्प्रिंकलर पूरे बगीचे को पानी देगा? (π = 3.14 लिया गया)
हल:
स्प्रिंकलर का गोलाकार क्षेत्रफल = πr 2
= 3.14 × 12 × 12
= 3.14 × 144 = 452.16 मी 2
गोलाकार फूलों के बगीचे का क्षेत्रफल = 314 मी 2
चूँकि गोलाकार फूलों के बगीचे का क्षेत्रफल स्प्रिंकलर के क्षेत्रफल से छोटा है
इसलिए, स्प्रिंकलर पूरे बगीचे को पानी देगा।

प्रश्न 15.
निम्नलिखित आकृति में दिखाए अनुसार आंतरिक और बाहरी वृत्तों की परिधि ज्ञात कीजिए? (π = 3.14 लीजिए)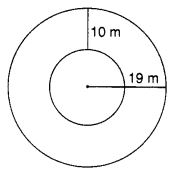

हल:
आंतरिक वृत्त की त्रिज्या = 19 – 10 = 9 मीटर
∴ आंतरिक वृत्त की परिधि = 2 πr = 2 × 3.14 × 9 मीटर = 56.52 सेमी
बाहरी वृत्त की त्रिज्या = 19 मीटर
∴ बाहरी वृत्त की परिधि = 2πr = 2 × 3.14 × 19 मीटर = 119.32 मीटर।

प्रश्न 16.
28 सेमी त्रिज्या वाले एक पहिये को 352 मीटर चलने के लिए कितनी बार घूमना होगा? ( π = 227 लीजिए)
हल:

प्रश्न 17.
एक वृत्ताकार घड़ी की मिनट की सुई 15 सेमी लंबी है। मिनट की सुई की नोक 1 घंटे में कितनी दूरी तय करती है? (π = 3.14 लीजिए)
हल:
हम जानते हैं कि मिनट की सुई एक घंटे में एक पूरा चक्कर लगाती है।
∴ इसकी नोक द्वारा तय की गई दूरी = 15 सेमी त्रिज्या वाले वृत्त की परिधि
= (2 × 3.14 × 15) सेमी
= 94.2 सेमी

Ex 11.4

प्रश्न 1.
एक बगीचा 90 मीटर लंबा और 75 मीटर चौड़ा है। इसके बाहर और चारों ओर 5 मीटर चौड़ा एक रास्ता बनाया जाना है। रास्ते का क्षेत्रफल ज्ञात कीजिए। साथ ही, बगीचे का क्षेत्रफल एक हेक्टेयर में ज्ञात कीजिए।
हल: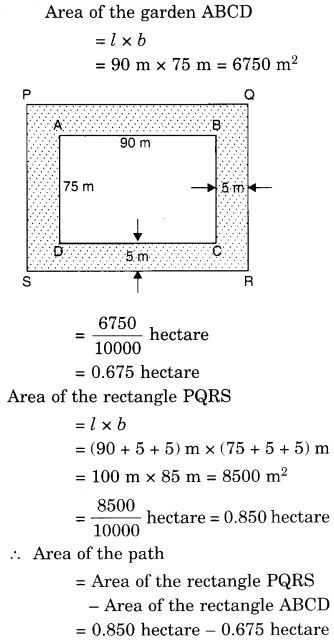

प्रश्न 2.
125 मीटर लंबे और 65 मीटर चौड़े एक आयताकार पार्क के बाहर और उसके चारों ओर 3 मीटर चौड़ा एक पथ बना हुआ है। पथ का क्षेत्रफल ज्ञात कीजिए।
हल:
PQ = 125 मीटर + 3 मीटर + 3 मीटर = 131 मीटर
QR = 65 मीटर + 3 मीटर + 3 मीटर = 71 मीटर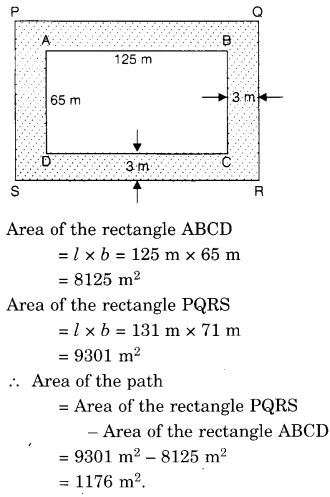

प्रश्न 3.
एक चित्र 8 सेमी लंबे और 5 सेमी चौड़े कार्डबोर्ड पर इस प्रकार बनाया गया है कि इसकी प्रत्येक भुजा पर 1.5 सेमी का मार्जिन है। मार्जिन का कुल क्षेत्रफल ज्ञात कीजिए।
हल: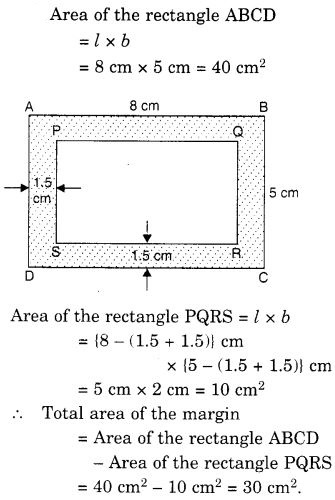

प्रश्न 4.
5.5 मीटर लंबे और 4 मीटर चौड़े एक कमरे के बाहरी भाग पर 2.25 मीटर चौड़ा एक बरामदा बनाया गया है। ज्ञात कीजिए:
(i) बरामदे का क्षेत्रफल
(ii) ₹200 प्रति वर्ग मीटर की दर से बरामदे के फर्श पर सीमेंट लगाने की लागत।
हल: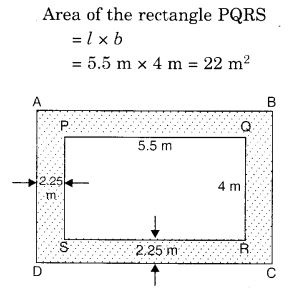

प्रश्न 5.
30 मीटर भुजा वाले एक वर्गाकार बगीचे के अंदर और किनारे के साथ 1 वर्ग मीटर चौड़ा एक रास्ता बनाया गया है। ज्ञात कीजिए:
(i) रास्ते का क्षेत्रफल।
(ii) बगीचे के शेष भाग में 40 डॉलर प्रति वर्ग मीटर की दर से घास लगाने की लागत।
हल: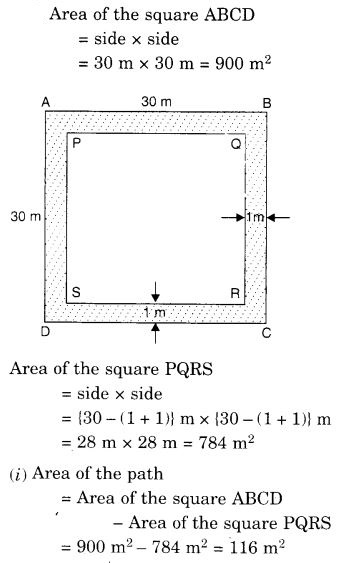

प्रश्न 6.
700 मीटर लंबे और 300 मीटर चौड़े एक आयताकार पार्क के केंद्र से होकर, उसकी भुजाओं के समांतर, दो चौराहे, जिनकी चौड़ाई 10 मीटर है, समकोण पर काटते हैं। सड़कों का क्षेत्रफल ज्ञात कीजिए। साथ ही, चौराहे को छोड़कर पार्क का क्षेत्रफल भी ज्ञात कीजिए। उत्तर हेक्टेयर में दीजिए।
हल: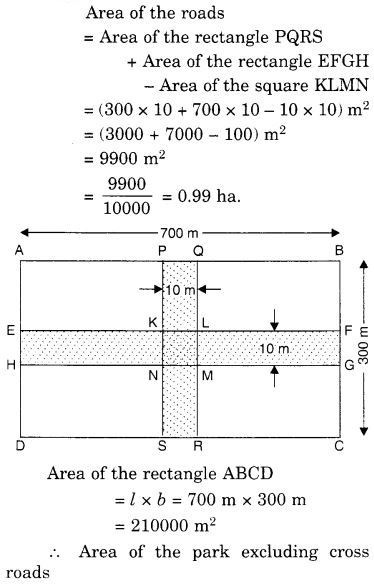

प्रश्न 7.
90 मीटर लंबाई और 60 मीटर चौड़ाई वाले एक आयताकार मैदान में दो सड़कें बनाई गई हैं जो भुजाओं के समानांतर हैं और एक दूसरे को खेत के केंद्र से समकोण पर काटती हैं। यदि प्रत्येक सड़क की चौड़ाई 3 मीटर है, तो
(i) सड़कों द्वारा कवर किया गया क्षेत्रफल ज्ञात कीजिए।
(ii) ₹ 110 प्रति वर्ग मीटर की दर से सड़कों के निर्माण की लागत।
हल:
(i) सड़कों द्वारा कवर किया गया क्षेत्रफल = आयत PQRS का क्षेत्रफल + आयत EFGH का क्षेत्रफल - वर्ग KLMN का क्षेत्रफल
= (90 × 3 + 60 × 3 – 3 × 3) वर्ग मीटर
= (270 + 180 – 9) वर्ग मीटर
= 441 वर्ग मीटर (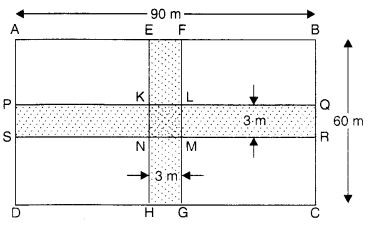

ii) ₹ 110 प्रति वर्ग मीटर की दर से सड़कों के निर्माण की लागत ₹ 441 × 110 = ₹ 48510.

प्रश्न 8.
प्रज्ञा ने 4 सेमी त्रिज्या वाले वृत्ताकार पाइप (संलग्न आकृति) के चारों ओर एक रस्सी लपेटी और रस्सी की आवश्यक लंबाई काट ली। फिर उसने इसे 4 सेमी भुजा वाले वर्गाकार बॉक्स (जैसा कि दिखाया गया है) के चारों ओर लपेट दिया। क्या उसके पास कोई रस्सी बची थी? = (π = 3.14)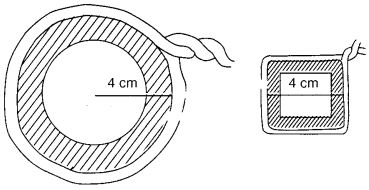

हल:
वृत्ताकार पाइप की त्रिज्या (r) = 4 सेमी
∴ वृत्ताकार पाइप की परिधि = 2πr = 2 × 3.14 × 4 सेमी = 25.12 सेमी
4 सेमी भुजा वाले वर्गाकार बॉक्स का परिमाप = 4 × भुजा = 4 × 4 सेमी = 16 सेमी
∵ 25.12 सेमी > 16 सेमी
∴ उसके पास अतिरिक्त रस्सी बची थी और रस्सी की लंबाई = (25.12 – 16) सेमी = 9.12 सेमी

प्रश्न 9.
निम्नलिखित आकृति एक आयताकार लॉन को दर्शाती है जिसके बीच में एक गोलाकार फूलों की क्यारी है। ज्ञात कीजिए:
(i) पूरी भूमि का क्षेत्रफल।
(ii) फूलों की क्यारी का क्षेत्रफल।
(iii) फूलों की क्यारी के क्षेत्रफल को छोड़कर लॉन का क्षेत्रफल।
(iv) फूलों की क्यारी की परिधि।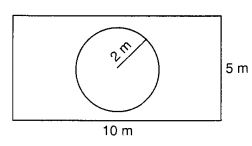

हल:

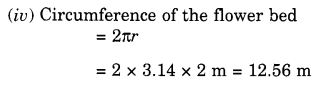
प्रश्न 10.
निम्नलिखित आकृतियों में, छायांकित भागों का क्षेत्रफल ज्ञात कीजिए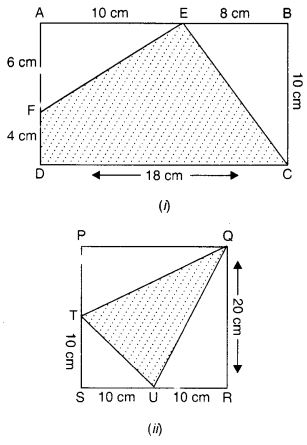

हल:

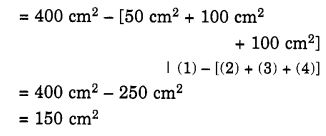
प्रश्न 11.
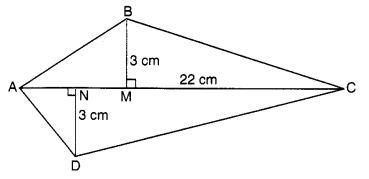
चतुर्भुज ABCD का क्षेत्रफल ज्ञात कीजिए।
यहाँ, AC = 22 सेमी, BM = 3 सेमी, DN = 3 सेमी, तथा BM ⊥ AC, DN ⊥ AC है।
हल:
चतुर्भुज ABCD का क्षेत्रफल = त्रिभुज ABC का क्षेत्रफल + त्रिभुज ADC का क्षेत्रफल