SikhLo - Current Affairs in Hindi, Daily current affairs, Current affairs

 NCERT Class 7 Maths Chapter 12 बीजीय व्यंजक

NCERT Solutions for Class 7 Maths Chapter 12 बीजीय व्यंजक

Ex 12.1

प्रश्न 1.
निम्नलिखित स्थितियों में चरों, अचरों और अंकगणितीय संक्रियाओं का उपयोग करके बीजीय व्यंजक प्राप्त करें।
(i) y में से z घटाना।
हल:
y – z

(ii) संख्याओं x और y के योग का आधा।
हल:
\(\frac{1}{2}\) (x -y)12  (x -y)

(iii) संख्या z को स्वयं से गुणा करने पर,
हल:
z × z अर्थात्, z 2

(iv) संख्या p और q के गुणनफल का एक-चौथाई।
हल:
\(\frac{1}{4}\) pq14 pq

(v) संख्याओं x और y दोनों का वर्ग और योग।
हल:
x 2 + y 2

(vi) संख्या 5 को संख्याओं m और n के गुणनफल के तिगुने में जोड़ा गया।
हल:
3mn + 5

(vii) संख्याओं y और z का गुणनफल 10 से घटाया गया।
हल:
10 – yz

(viii) संख्याओं a और 6 के योग को उनके गुणनफल से घटाया जाता है।
हल:
ab – (a + b)

प्रश्न 2.
(i) निम्नलिखित व्यंजकों में पदों और उनके गुणनखंडों की पहचान कीजिए। पदों और गुणनखंडों को वृक्ष आरेखों द्वारा दर्शाइए:

(a) एक्स - 3
(b) 1 + एक्स + एक्स 2
(c) वाई - वाई 3
(d) 5xy 2 + 7x 2 वाई
(e) -एबी + 2बी 2 -3ए 2

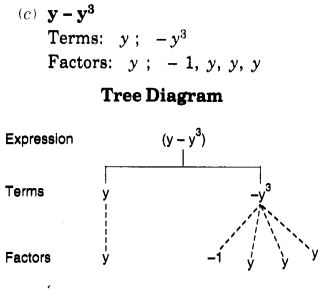
(ii) नीचे दिए गए व्यंजकों में पदों और कारकों की पहचान कीजिए :

(a) – 4x + 5
(b) – 4x + 5y
(c) 5y + 3y 2
(d) xy + 2x 2 y 2
(e) pq + q
(f) 1.2 ab -2.4 b + 3.6 a
(g) \(\frac { 3 }{ 4 } \) x + \(\frac { 1 }{ 4 } \) (h) 0.1 p 2 + 0.2 q 234 x + 14

हल: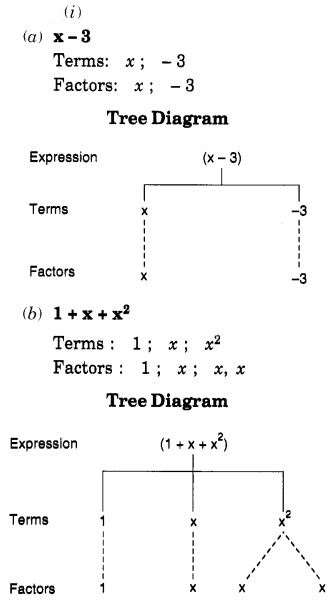

प्रश्न 3.
निम्नलिखित व्यंजकों में पदों (स्थिरांकों के अलावा) के संख्यात्मक गुणांकों की पहचान कीजिए:

1. 5 – 3टी 2
2. 1 + टी + टी 2 + टी 3
3. एक्स + 2xy + 3y
4. 100मी + 1000एन
5. -पी 2 क्यू 2 + 7पीक्यू
6. 1.2 ए + 0.8 बी
7. 3.14 आर 2
8. 2 (एल + बी)
9. 0.1 y + 0.01 y 2 .

हल:

प्रश्न 4.
(a) उन पदों की पहचान कीजिए जिनमें x हो तथा x का गुणांक दीजिए।

1. y 2 x + y
2. 13y 2 – 8yx
3. एक्स + वाई + 2
4. 5 + z + zx
5. 1 + x + xy
6. 12xy 2 + 25
7. 7x + xy 2 .

(b) उन पदों की पहचान करें जिनमें y 2 शामिल है और y 2 का गुणांक दें ।

1. 8 – xy 2
2. 5y 2 + 7x
3. 2x 2 y – 15xy 2 + 7y 2

हल:

प्रश्न 5.
एकपदी, द्विपद और त्रिपद में वर्गीकृत करें।

1. 4y – 7z
2. य 2
3. x + y – xy
4. 100
5. अब – ए – बी
6. 5 – 3टी
7. 4p 2 q – 4pq 2
8. 7 मिनट
9. z 2 – 3z + 8 a 2 + b 2
10. z 2 + z
11. 1 + x+ x 2

हल:
हम जानते हैं कि केवल एक पद वाला बीजीय व्यंजक एकपदी कहलाता है। अतः, एकपदी हैं: (ii), (iv), और (viii)।

हम जानते हैं कि दो पदों वाले बीजीय व्यंजक को द्विपद कहते हैं। अतः, द्विपद हैं: (i), (vi), (vii), (x) और (xi)।

हम जानते हैं कि तीन पदों वाला बीजीय व्यंजक त्रिपद कहलाता है। अतः, त्रिपद हैं: (iii), (v), (ix) और (xii)।

प्रश्न 6.
बताइए कि दिए गए पदों का युग्म समान पदों का है या असमान पदों का :
(i) 1, 100
हल:
समान पदों का

(ii) -7x, \(\frac{5}{2}\)x हल: जैसे52x

(iii) – 29x, – 29y
हल:
भिन्न

(iv)14xy, 42yx
हल:
जैसे

(v) 4m 2 p, 4mp 2
उत्तर:
भिन्न

(vi) 12xz, 12x 2 z 2
हल:
भिन्न

(i) 4y – 7z.
यह व्यंजक द्विपद है क्योंकि इसमें दो पद हैं: 4y और – Iz.
(ii) y 2.
यह व्यंजक एकपदी है क्योंकि इसमें केवल एक पद है: y 2.
(iii) x + y – xy. यह
व्यंजक त्रिपद है क्योंकि इसमें तीन पद हैं: x, y, और – xy.
(iv) 100.
यह व्यंजक एकपदी है क्योंकि इसमें केवल एक पद है: 100.
(v) ab – a – b.
यह व्यंजक त्रिपद है क्योंकि इसमें तीन पद हैं: ab, -a, और -b. ( vi)
5 – 3t. यह
व्यंजक द्विपद है क्योंकि इसमें दो पद हैं: 5 और – 31.
(vii) 4p 2 q – 4pq 2.
यह व्यंजक द्विपद है क्योंकि इसमें दो पद हैं: 4p 2 q यह व्यंजक एकपदी है क्योंकि इसमें केवल एक पद है : 7mn. (ix) z 2 – 3z + 8. यह व्यंजक त्रिपद है क्योंकि इसमें तीन पद हैं : z 2 , – 3z और 8. (x) a 2 + b 2. यह व्यंजक द्विपद है क्योंकि इसमें दो पद हैं : a 2 और b 2. ( xi ) z 2 + z. यह व्यंजक द्विपद है क्योंकि इसमें दो पद हैं : z 2 और z. ( xii) 1 + x + x 2. यह व्यंजक त्रिपद है क्योंकि इसमें तीन पद हैं : 1, x, और x 2 .

प्रश्न 6.
बताइए कि दिए गए पदों का युग्म समान पदों का है या असमान पदों का :
(i) 1, 100
हल:
समान पदों का

(ii) -7x, \(\frac{5}{2}\)x हल: जैसे52x

(iii) – 29x, – 29y
हल:
भिन्न

(iv)14xy, 42yx
हल:
जैसे

(v) 4m 2 p, 4mp 2
उत्तर:
भिन्न

(vi) 12xz, 12x 2 z 2
हल:
भिन्न

प्रश्न 7.
निम्नलिखित में समान पदों की पहचान कीजिए :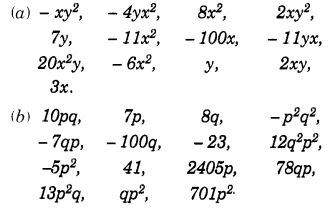

हल:

Ex 12.2

प्रश्न 1.
समान पदों को संयोजित करना सरल कीजिए:

1. 21b – 32 + 7b – 20b
2. – z2 + 13z2 – 5z + 7z3 – 15z
3. p – (p – q) – q – (q – p)
4. 3a – 2b – ab – (a – b + ab) + 3ab + b – a
5. 5x2y – 5x2 + 3yx2 – 3y2 + x2 – y2 + 8xy2 – 3y2
6. (3y2 + 5y – 4) – (8y – y2 – 4).

समाधान: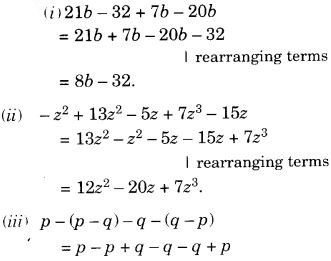

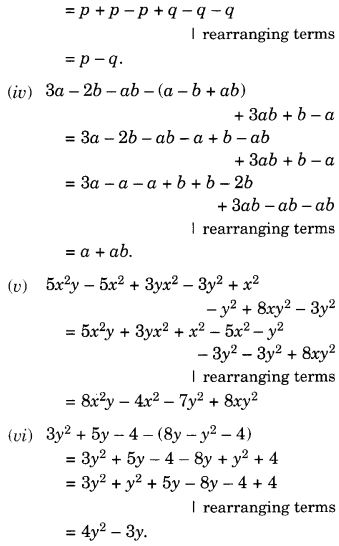
प्रश्न 2.
जोड़ें: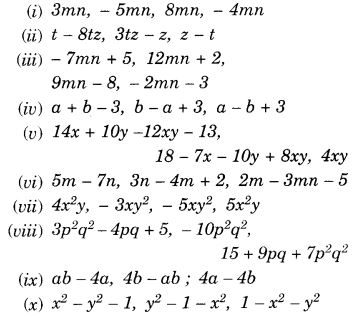

समाधान: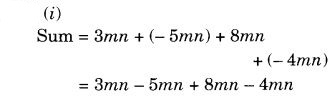

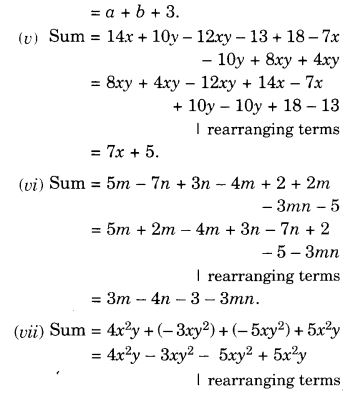
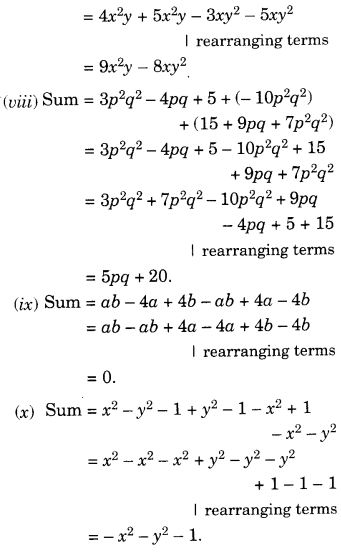
प्रश्न 3.
घटाएँ:

1. y 2 से -5y 2
2. 6xy से – 12xy
3. (a – b) से (a + b)
4. a (b – 5) से b (5 – a)
5. -m 2 + 5mn से 4m 2 – 3mn + 8
6. -x 2 + 10x – 5 से 5x – 10
7. 5a 2 - 7ab + 5b 2 से 3ab - 2a 2 - 2b 2
8. 5p2 + 3q2 – pq से 4pq – 5q2 – 3p2.

समाधान: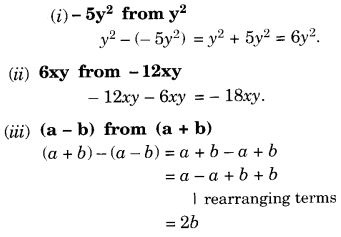

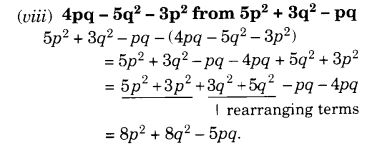
प्रश्न 4.
(a) 2x 2 + 3xy प्राप्त करने के लिए x 2 + xy + y 2 में क्या जोड़ा जाना चाहिए ? 

(b) -3a + 76 + 16 प्राप्त करने के लिए 2a + 8b + 10 में से क्या घटाया जाना चाहिए? 

हल: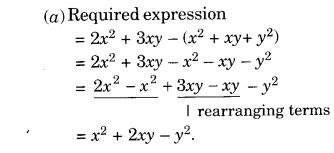

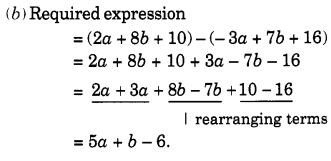
प्रश्न 5. -x 2 – y 2 + 6xy + 20 प्राप्त करने के लिए 3x 2 – 4y 2 + 5xy + 20 में से क्या घटाना चाहिए?
हल: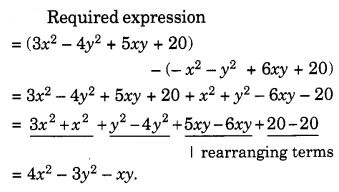

प्रश्न 6.
(a) 3x – y + 11 और – y – 11 के योग में से 3x – y – 11 घटाएँ।
(b) 4 + 3x और 5 – 4x + 2x 2 के योग में से 3x 2 – 5x और -x 2 + 2x + 5का योग घटाएँ।
हल: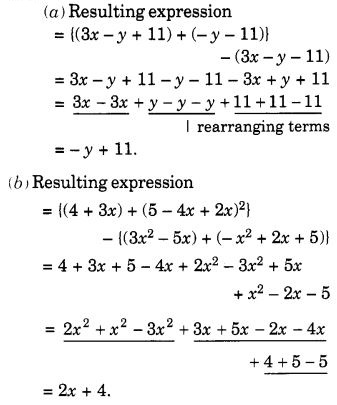

Ex 12.3

प्रश्न 1.
यदि m = 2 है, तो का मान ज्ञात कीजिए:

1. मी – 2
2. 3 मी – 5
3. 9 – 5 मी
4. 3मी 2 – 2मी – 7
5. 5m2 – 4

हल: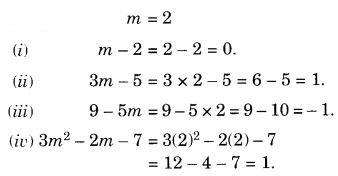

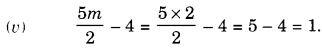
प्रश्न 2.
यदि p = - 2, तो का मान ज्ञात कीजिए:

1. 4पी + 7
2. – 3पी 2 + 4पी + 7
3. – 2पी 3 – 3पी 2 + 4पी + 7.

हल: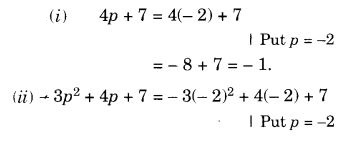

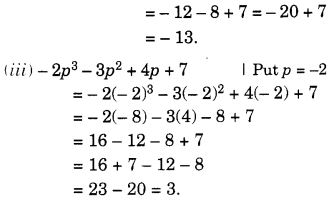
प्रश्न 3.
निम्नलिखित व्यंजकों का मान ज्ञात कीजिए, जब x = – 1 :

1. 2x – 7
2. – x + 2
3. एक्स 2 + 2x + 1
4. 2x 2 – x – 2.

हल: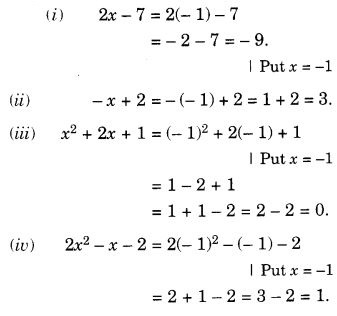

प्रश्न 4.
यदि a = 2, b = – 2, तो का मान ज्ञात कीजिए:

1. ए 2 + बी 2
2. ए 2 + एबी + बी 2
3. ए 2 – बी 2 .

हल: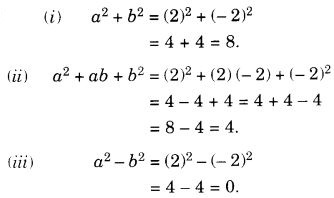

प्रश्न 5.
जब a = 0, b = - 1, तो दिए गए व्यंजकों का मान ज्ञात कीजिए:

1. 2a + 2b
2. 2a 2 + b 2 + 1
3. 2a 2 b + 2ab 2 + ab
4. ए 2 + एबी + 2.

हल: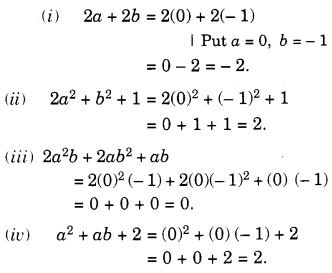

प्रश्न 6.
व्यंजकों को सरल कीजिए और मान ज्ञात कीजिए यदि x, 2 के बराबर है।

1. एक्स + 7 + 4 (एक्स – 5)
2. 3 (x + 2) + 5x – 7
3. 6x + 5 (x – 2)
4. 4 (2x – 1) + 3x + 11.

हल: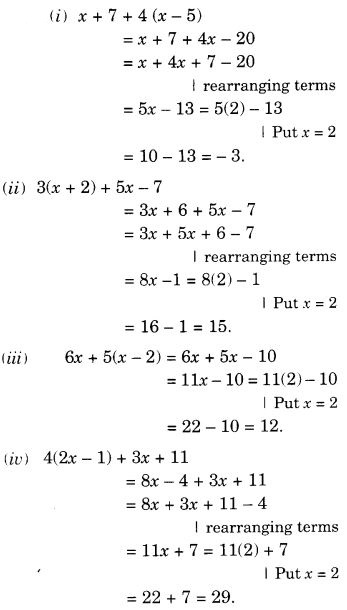

प्रश्न 7.
इन व्यंजकों को सरल कीजिए तथा उनके मान ज्ञात कीजिए यदि x = 3, a = – 1, b = – 2.

1. 3x – 5 – x + 9
2. 2 – 8x + 4x + 4
3. 3a + 5 – 8a + 1
4. 10 – 3बी – 4 – 5बी
5. 2ए – 2बी – 4 – 5 + ए.

हल:

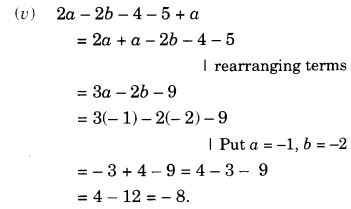
प्रश्न 8.
(i) यदि z = 10 है, तो z 3 – 3(z – 10)का मान ज्ञात कीजिए
। (ii) यदि p = -10 है, तो p 2 – 2p – 100का मान ज्ञात कीजिए।
हल: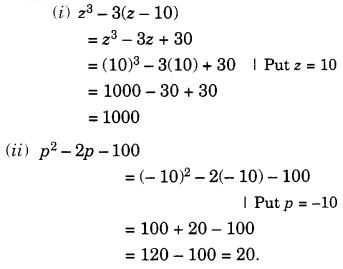

प्रश्न 9. 

यदि 2x 2 + x – a का मान 5 के बराबर हो, जब x = 0 हो, तो a का मान क्या होना चाहिए ? 
हल: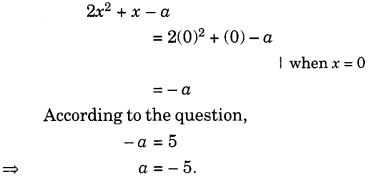

प्रश्न 10.
व्यंजक को सरल कीजिए और इसका मान ज्ञात कीजिए जब a = 5 और b = – 3 2(a 2 + ab) + 3 – ab.
हल: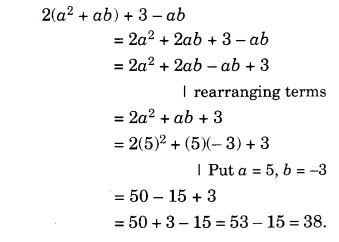

Ex 12.4

प्रश्न 1.
समान लंबाई के रेखाखंडों से बने अंकों के पैटर्न को देखिए। आपको ऐसे खंडित अंक इलेक्ट्रॉनिक घड़ियों या कैलकुलेटर के डिस्प्ले पर मिलेंगे।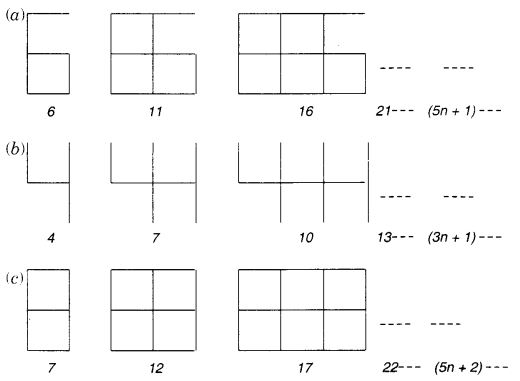

यदि बनने वाले अंकों की संख्या n ली जाए, तो n अंक बनाने के लिए आवश्यक खंडों की संख्या प्रत्येक पैटर्न के दाईं ओर दिए गए बीजीय व्यंजक द्वारा दी गई है।
इस प्रकार के 5, 10, 100 अंक बनाने के लिए कितने खंडों की आवश्यकता होगी?

हल:

मान लीजिए बनने वाले अंकों की संख्या n है, तो n अंक बनाने के लिए आवश्यक खंडों की संख्या बीजीय व्यंजक 5n + 1 द्वारा दी गई है।
अतः,

1. इस प्रकार के 5 अंक बनाने के लिए आवश्यक खंडों की संख्या = 5 × 5 + 1 = 25 + 1 = 26
2. इस प्रकार के 10 अंक बनाने के लिए आवश्यक खंडों की संख्या = 5 × 10 + 1 = 50 + 1 = 51
3. इस प्रकार के 100 अंक बनाने के लिए आवश्यक खंडों की संख्या = 5 × 100 + 1 = 500 + 1 = 501.

मान लीजिए बनने वाले अंकों की संख्या n है। तब, n अंक बनाने के लिए आवश्यक खंडों की संख्या बीजीय व्यंजक 3n + 1 द्वारा दी जाती है।
अतः,

1. इस प्रकार के 5 अंक बनाने के लिए आवश्यक खंडों की संख्या = 3 × 5 + 1 = 15 + 1 = 16
2. इस प्रकार के 10 अंक बनाने के लिए आवश्यक खंडों की संख्या = 3 × 10 + 1 = 30 + 1 = 31
3. इस प्रकार के 100 अंक बनाने के लिए आवश्यक खंडों की संख्या = 3 × 100 + 1 = 300 + 301.

मान लीजिए बनने वाले अंकों की संख्या n है। तब, n अंक बनाने के लिए आवश्यक खंडों की संख्या बीजीय व्यंजक 5n + 2 द्वारा दी गई है।
अतः,

1. इस प्रकार के 5 अंक बनाने के लिए आवश्यक खंडों की संख्या = 5 × 5 + 2 = 25 + 2 = 27
2. इस प्रकार के 10 अंक बनाने के लिए आवश्यक खंडों की संख्या = 5 × 10 + 2 = 50 + 2 = 52
3. इस प्रकार के लू अंक बनाने के लिए आवश्यक खंडों की संख्या = 5 × 100 + 2 = 500 + 2 = 502.

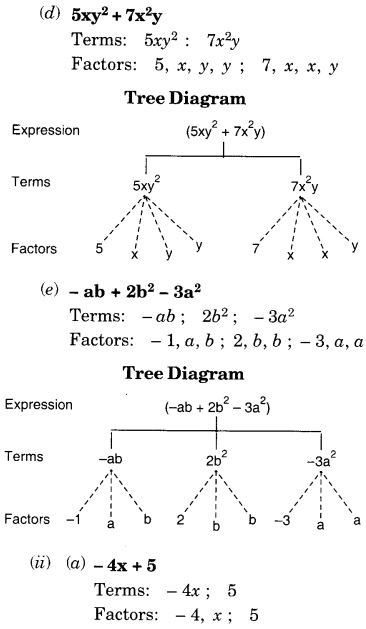
प्रश्न 2.
संख्या पैटर्न की तालिका को पूरा करने के लिए दिए गए बीजीय व्यंजक का प्रयोग कीजिए।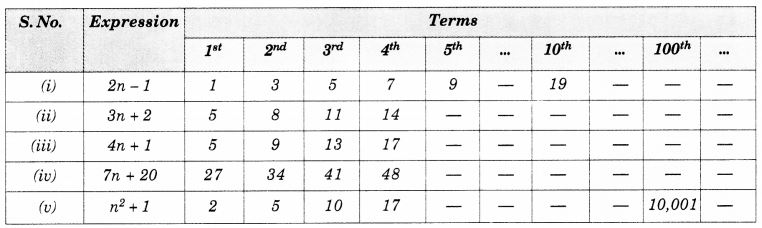

हल: