NCERT Class 7 Maths Chapter 14 सममिति
NCERT Solutions for Class 7 Maths Chapter 14 सममिति
Ex 14.1
प्रश्न 1.
छिद्रित आकृतियों की प्रतिलिपि बनाइए और निम्नलिखित के लिए सममिति अक्ष ज्ञात कीजिए :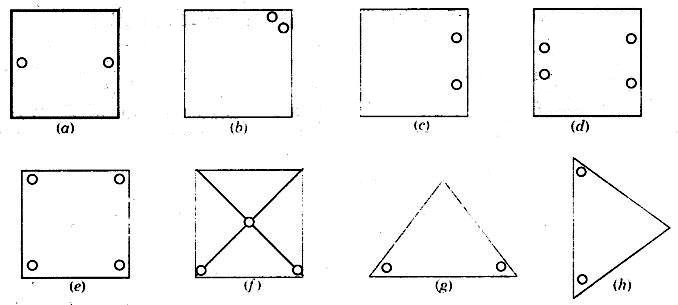
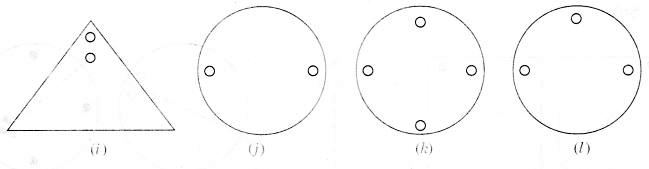
हल: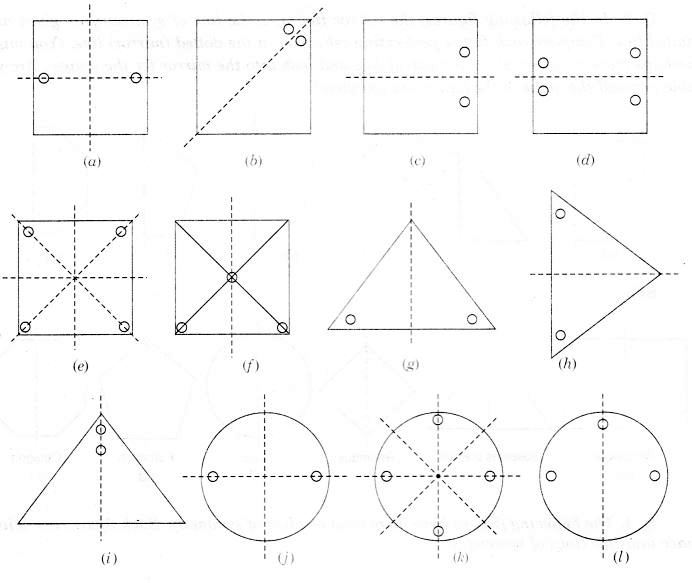
प्रश्न 2.
सममित रेखा(एँ) दी गई हैं, अन्य छिद्र ज्ञात कीजिए: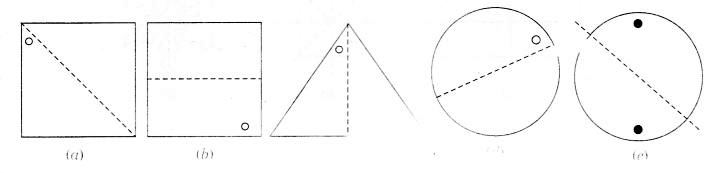
हल: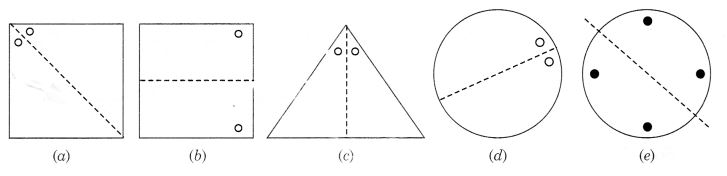
प्रश्न 3.
निम्नलिखित आकृतियों में, दर्पण रेखा (अर्थात सममित रेखा) एक बिंदीदार रेखा के रूप में दी गई है। प्रत्येक आकृति को बिंदीदार (दर्पण) रेखा में परावर्तन करके पूरा कीजिए। (आप बिंदीदार रेखा के साथ एक दर्पण रख सकते हैं और प्रतिबिंब के लिए दर्पण में देख सकते हैं)। क्या आप उस आकृति का नाम याद कर पा रहे हैं जिसे आपने पूरा किया है?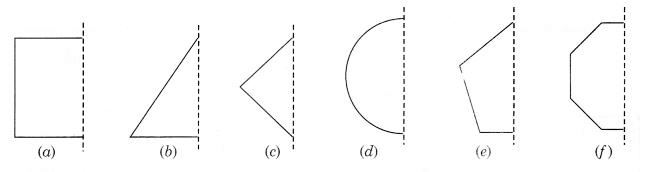
हल: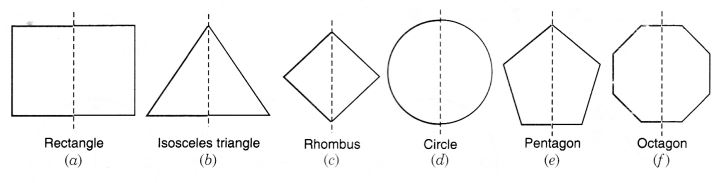
प्रश्न 4.
निम्नलिखित आकृतियों में एक से अधिक सममित रेखाएँ हैं। ऐसी आकृतियों को एकाधिक सममित रेखाएँ कहा जाता है: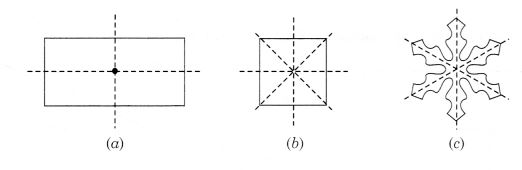
निम्नलिखित प्रत्येक आकृति में, यदि कोई हो, तो एकाधिक सममित रेखाओं की पहचान कीजिए: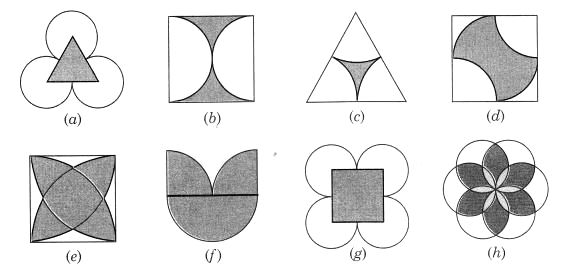
हल: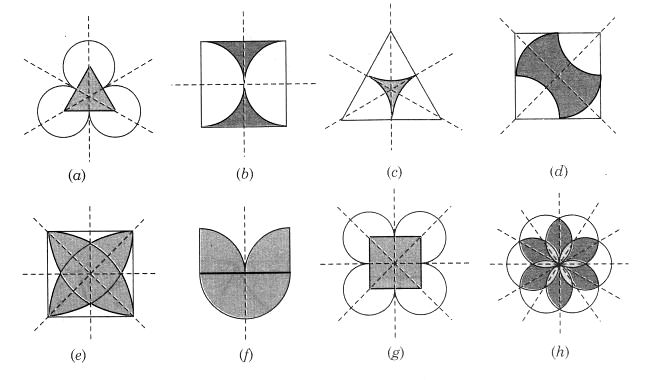
प्रश्न 5.
यहाँ दी गई आकृति की प्रतिलिपि बनाएँ। किसी एक विकर्ण को सममित रेखा मानकर, आकृति को एक विकर्ण के सापेक्ष सममित बनाने के लिए कुछ और वर्गों को छायांकित करें। क्या ऐसा करने के एक से अधिक तरीके हैं? क्या आकृति दोनों विकर्णों के सापेक्ष सममित होगी?
हल: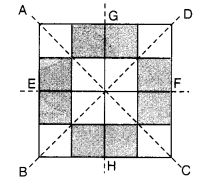
हाँ! आकृति को सममित बनाने के एक से अधिक तरीके हैं।
- आइए हम विकर्ण BD लें और आकृति में दर्शाए अनुसार वर्गों को छायांकित करें ताकि आकृति BD के प्रति सममित हो जाए।
- इसी प्रकार, आकृति विकर्ण AC के प्रति सममित है। इस प्रकार, आकृति दोनों विकर्णों के प्रति सममित है।
- यह आकृति EF और GH के प्रति भी सममित है।
प्रश्न 6.
आरेख की प्रतिलिपि बनाएँ और प्रत्येक आकृति को दर्पण रेखा(ओं) के प्रति सममित बनाने के लिए पूरा करें: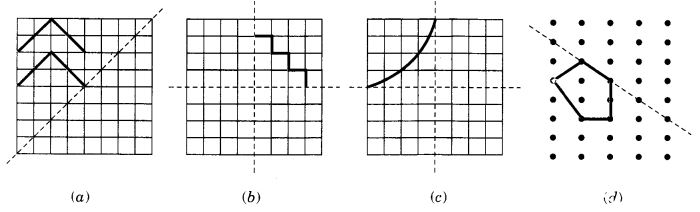
हल: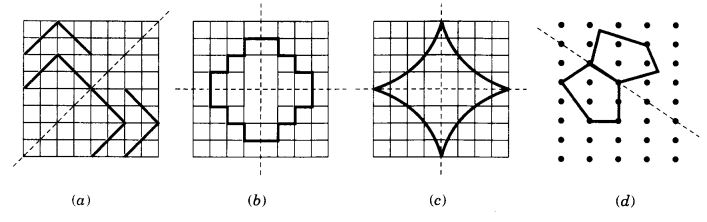
प्रश्न 7.
निम्नलिखित आकृतियों के लिए सममित रेखाओं की संख्या बताइए:
(a) एक समबाहु त्रिभुज
(b) एक समद्विबाहु त्रिभुज
(c) एक विषमबाहु त्रिभुज
(d) एक वर्ग
(e) एक आयत
(f) एक समचतुर्भुज
(g) एक समांतर
चतुर्भुज (h) एक चतुर्भुज
(i) एक सम षट्भुज
(j) एक वृत्त।
हल: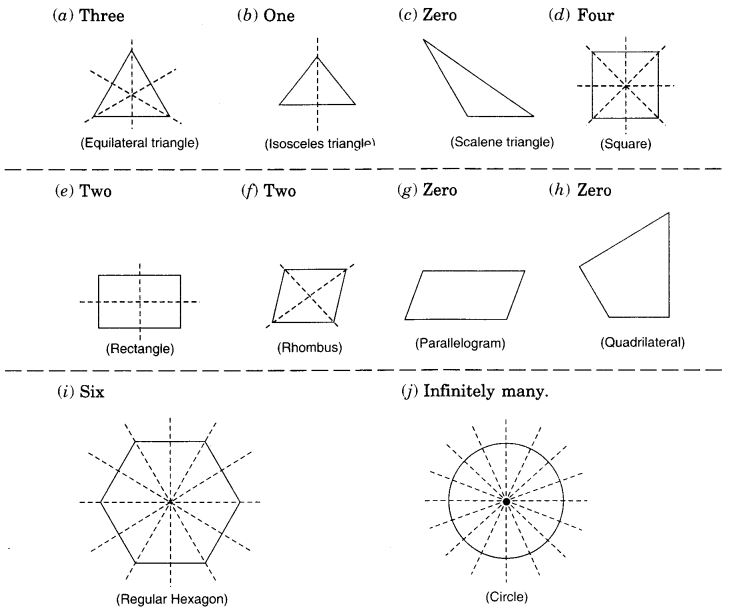
प्रश्न 8.
अंग्रेजी वर्णमाला के किन अक्षरों में परावर्तन सममिति (अर्थात दर्पण परावर्तन से संबंधित सममिति) होती है?
(a) एक ऊर्ध्वाधर दर्पण के प्रति
(b) एक क्षैतिज दर्पण के प्रति
(c) क्षैतिज और ऊर्ध्वाधर दोनों दर्पणों के प्रति।
हल:
प्रश्न 9.
बिना सममित रेखा वाली आकृतियों के तीन उदाहरण दीजिए।
हल: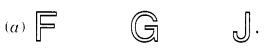
(b) एक विषमबाहु त्रिभुज,
(c) एक समांतर चतुर्भुज
प्रश्न 10.
सममिति रेखा को आप और क्या नाम दे सकते हैं?
- एक समद्विबाहु त्रिभुज?
- एक चक्र?
हल:
- मंझला
- व्यास
Ex 14.2
प्रश्न 1.
निम्नलिखित में से किस आकृति में क्रम 1 से अधिक की घूर्णन सममिति है?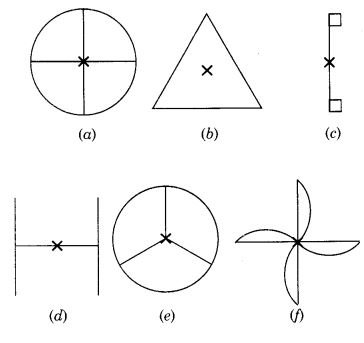
हल:
आकृतियाँ (a), (b), (d), (e) और (f) में क्रम 1 से अधिक की घूर्णन सममिति है।
प्रश्न 2.
प्रत्येक आकृति के लिए घूर्णन सममिति का क्रम दीजिए :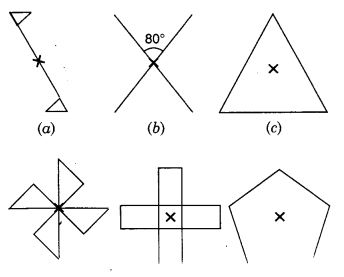
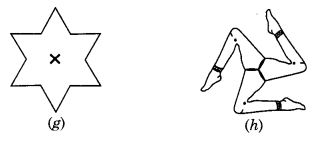
हल:
(a) → 2
(b) → 2
(c) → 3
(d) → 4
(e) → 4
(f) → 5
(g) → 6
(h) → 3
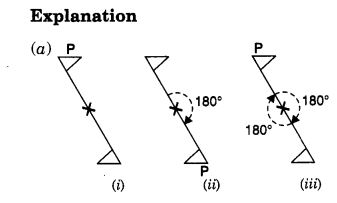
आकृति (i) में दर्शाए अनुसार एक बिंदु P अंकित कीजिए। हम देखते हैं कि एक पूर्ण घूर्णन में, दो स्थितियाँ ऐसी होती हैं (180° और 360° कोणों से घूमने पर) जब आकृति बिल्कुल एक जैसी दिखाई देती है। इस कारण, इसमें क्रम 2 की घूर्णन सममिति होती है।
आकृति (i) में दर्शाए अनुसार एक बिंदु P अंकित कीजिए। हम देखते हैं कि एक पूर्ण घूर्णन में, दो स्थितियाँ ऐसी होती हैं (180° और 360° कोणों से घूमने पर) जब आकृति बिल्कुल एक जैसी दिखती है।
इस कारण, इसमें क्रम 2 की घूर्णन सममिति है।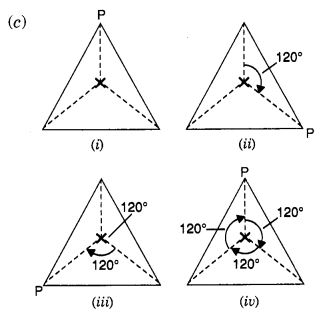
आकृति (i) में दर्शाए अनुसार एक बिंदु P अंकित कीजिए। हम देखते हैं कि एक पूर्ण घूर्णन में, तीन स्थितियाँ ऐसी होती हैं (कोणों 120°, 240° और 360° से घूमने पर) जब आकृति बिल्कुल एक जैसी दिखाई देती है। इस कारण, इसकी घूर्णन सममिति क्रम 3 है।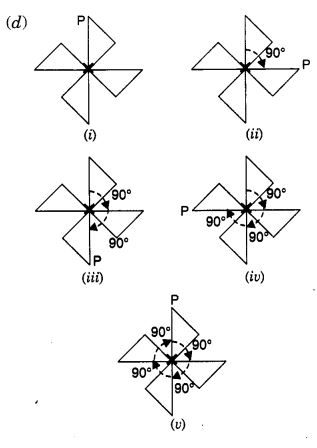
आकृति (i) में दर्शाए अनुसार एक बिंदु P अंकित कीजिए। हम देखते हैं कि एक पूर्ण घूर्णन में, चार स्थितियाँ ऐसी होती हैं (कोणों 90°, 180°, 270° और 360° से घूमने पर) जब आकृति बिल्कुल एक जैसी दिखाई देती है। इस कारण, हम कहते हैं कि इसमें क्रम 4 की घूर्णन सममिति है।
इसी प्रकार,
(e) एक पूर्ण घुमाव में, चार स्थितियाँ होती हैं (कोणों 90°, 180°, 270° और 360° से घूमने पर) जब आकृति बिल्कुल एक जैसी दिखती है।
∴ इसमें क्रम 4 की घूर्णन सममिति है।
(f) यह आकृति एक समपंचभुज है। एक पूर्ण चक्कर में, पाँच स्थितियाँ ऐसी हैं (कोणों 72°, 144°, 216°, 288° और 360° से घूमने पर) जब आकृति बिल्कुल एक जैसी दिखती है।
∴ इसमें क्रम 5 की घूर्णन सममिति है।
(g) एक पूर्ण चक्कर में, छः स्थितियाँ होती हैं (कोणों 60°, 120°, 180°, 240°, 300° और 360° से घूमने पर) जब आकृति बिल्कुल एक जैसी दिखती है।
इसमें क्रम 6 की घूर्णन सममिति है।
(h) एक पूर्ण चक्कर में, तीन स्थितियाँ होती हैं (कोणों 120°, 240° और 360° से घूमने पर) जब आकृति बिल्कुल एक जैसी दिखती है।
∴ इसमें क्रम 3 की घूर्णन सममिति है।
Ex 14.3
प्रश्न 1.
ऐसी दो आकृतियों के नाम लिखिए जिनमें रैखिक सममिति और घूर्णन सममिति दोनों हों।
हल:
ऐसी दो आकृतियाँ जिनमें रैखिक सममिति और घूर्णन सममिति दोनों हों, एक समबाहु त्रिभुज और एक वृत्त हैं।
प्रश्न 2.
जहाँ तक संभव हो,
(i) एक त्रिभुज जिसमें क्रम 1 से अधिक की रैखिक सममिति तथा घूर्णन सममिति दोनों हों।
(ii) एक त्रिभुज जिसमें केवल रैखिक सममिति हो तथा क्रम 1 से अधिक की घूर्णन सममिति न हो।
(iii) एक चतुर्भुज जिसमें क्रम 1 से अधिक की घूर्णन सममिति हो, परन्तु रैखिक सममिति न हो, का एक कच्चा चित्र बनाइए।
(iv) एक चतुर्भुज जिसमें रैखिक सममिति हो, लेकिन क्रम 1 से अधिक की घूर्णन सममिति न हो।
हल:
(i) एक समबाहु त्रिभुज में 3 सममिति रेखाएं और क्रम 3 की घूर्णन सममिति होती है।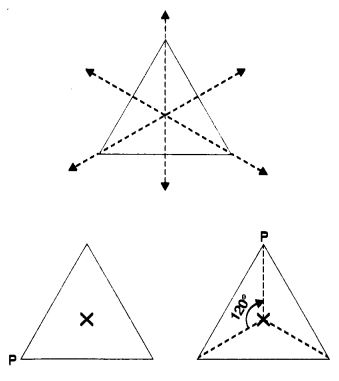
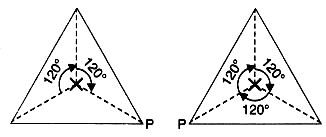
(ii) एक समद्विबाहु त्रिभुज में केवल एक रैखिक सममिति होती है, लेकिन क्रम 1 से अधिक की कोई घूर्णन सममिति नहीं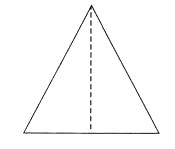
होती है । (iii) एक समांतर चतुर्भुज में कोई सममिति रेखा नहीं होती है, लेकिन क्रम 2 की घूर्णन सममिति होती है।
(iv) एक समद्विबाहु समलम्ब में एक सममिति रेखा होती है, लेकिन क्रम 1 से अधिक की कोई घूर्णन सममिति नहीं होती है।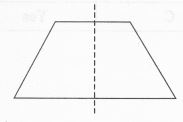
प्रश्न 3.
यदि किसी आकृति में दो या अधिक सममित रेखाएँ हों, तो क्या उसमें क्रम 1 से अधिक की घूर्णन सममिति होनी चाहिए?
उत्तर:
हाँ
प्रश्न 4.
रिक्त स्थान भरें: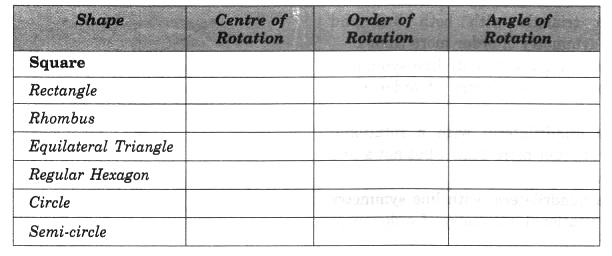
हल: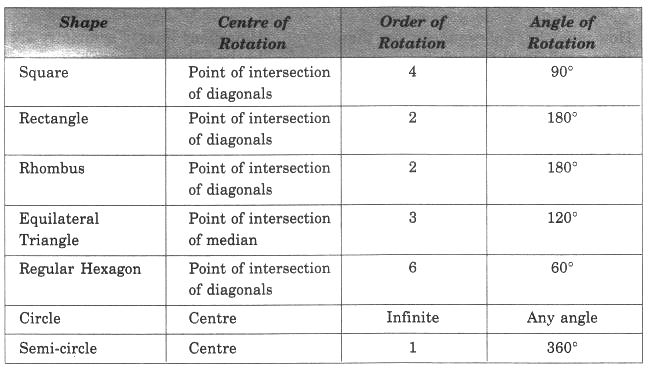
प्रश्न 5.
उन चतुर्भुजों के नाम बताइए जिनमें रैखिक सममिति और घूर्णन सममिति दोनों क्रम 1 से अधिक हों।
हल:
उन चतुर्भुजों का नाम वर्ग है जिनमें रैखिक सममिति और घूर्णन सममिति दोनों क्रम 1 से अधिक हों।
प्रश्न 6.
एक आकृति को केंद्र के परितः 60° घुमाने पर वह अपनी मूल स्थिति जैसी ही दिखाई देती है। आकृति के लिए यह अन्य किन कोणों पर घटित होगा?
हल:
अन्य कोण 120°, 180°, 240°, 300° और 360° हैं।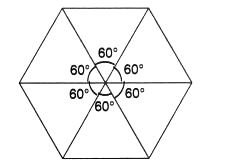
प्रश्न 7.
क्या हम क्रम 1 से अधिक की घूर्णन सममिति प्राप्त कर सकते हैं जिसका घूर्णन कोण
(i) 45° है?
(ii) 17° है?
हल:
(i) हाँ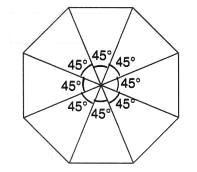
(ii) नहीं
