NCERT Class 8 Maths Chapter 10 ठोस आकृतियों का चित्रण
NCERT Solutions for Class 8 Maths Chapter 10 ठोस आकृतियों का चित्रण
Ex 10.1
प्रश्न 1.
दिए गए प्रत्येक ठोस के लिए, दो दृश्य दिए गए हैं। प्रत्येक ठोस के लिए संगत ऊपरी और अग्र दृश्य का मिलान कीजिए। पहला दृश्य आपके लिए किया गया है।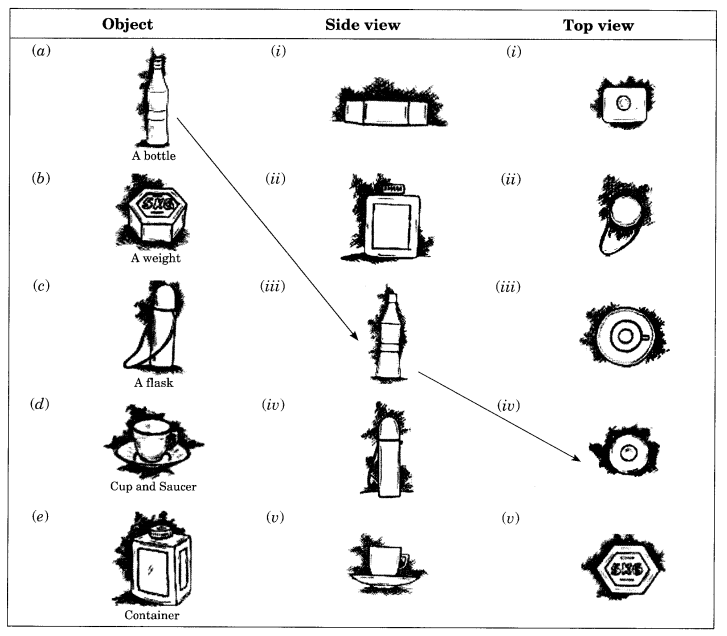
हल:
(a) एक बोतल → (iii) → (iv)
(b) एक भार → (i) → (v)
(c) एक फ्लास्क → (iv) → (ii)
(d) कप और तश्तरी → (v) → (iii)
(e) पात्र → (ii) → (i)
प्रश्न 2.
दिए गए प्रत्येक ठोस के लिए तीन दृश्य दिए गए हैं। प्रत्येक ठोस के लिए संगत शीर्ष, अग्र और पार्श्व दृश्य पहचानिए।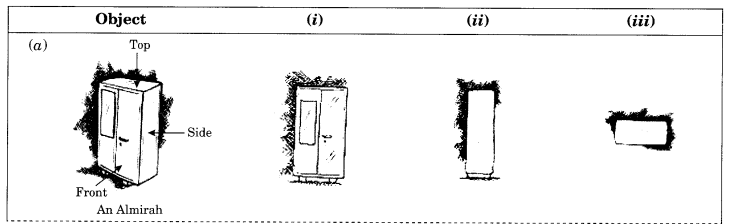
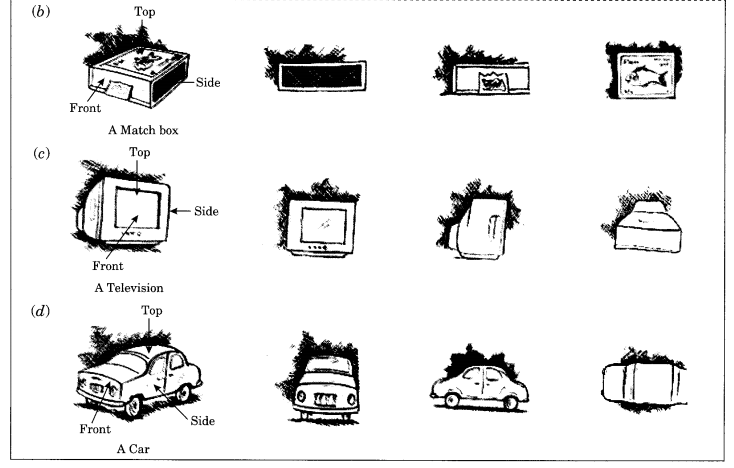
हल:
(a) एक अलमारी → (i) सामने → (ii) भुजा → (iii) ऊपर
(b) एक माचिस → (i) भुजा → (it) सामने → (iii) ऊपर
(c) एक टेलीविजन → (i) सामने → (ii) भुजा → (iii) ऊपर
(d) एक कार → (i) सामने → (ii) भुजा → (iii) ऊपर
प्रश्न 3.
प्रत्येक दिए गए ठोस के लिए, शीर्ष दृश्य, अग्र दृश्य और पार्श्व दृश्य की पहचान करें।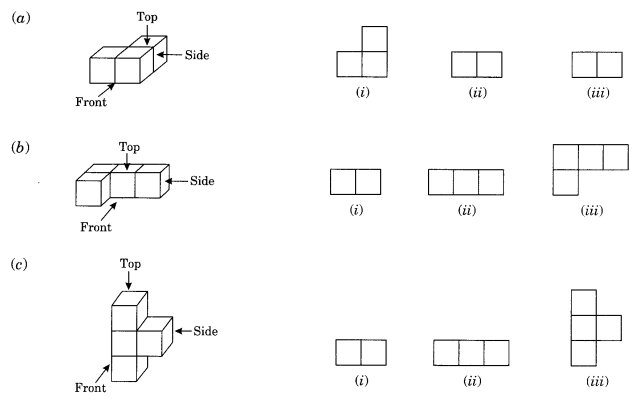
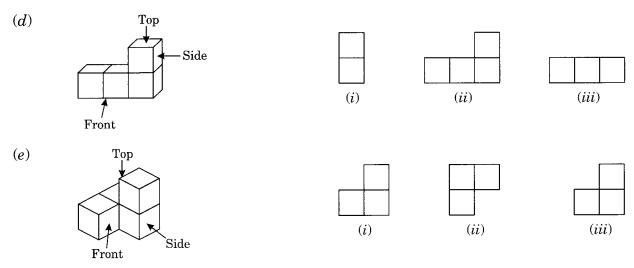
हल:
(a) (i) शीर्ष → (ii) सामने → (iii) भुजा
(b) (i) भुजा → (ii) सामने → (iii) शीर्ष
(c) (i) शीर्ष → (ii) भुजा → (iii) सामने
(d) (i) भुजा → (ii) सामने → (iii) शीर्ष
(e) (i) सामने → (ii) शीर्ष → (iii) भुजा
प्रश्न 4.
दी गई वस्तुओं का अग्र दृश्य, पार्श्व दृश्य और शीर्ष दृश्य बनाइए।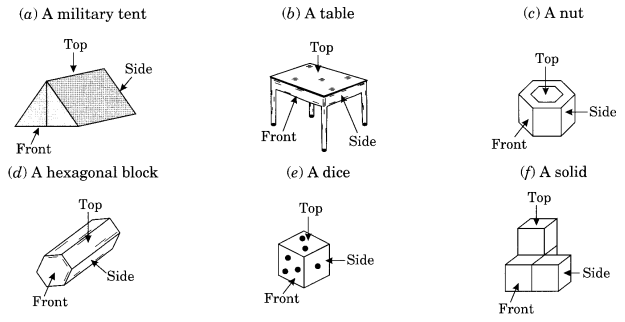
हल: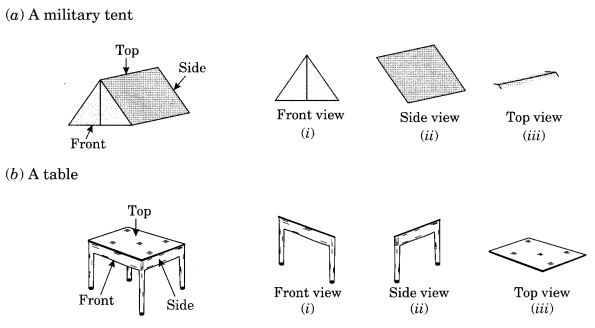
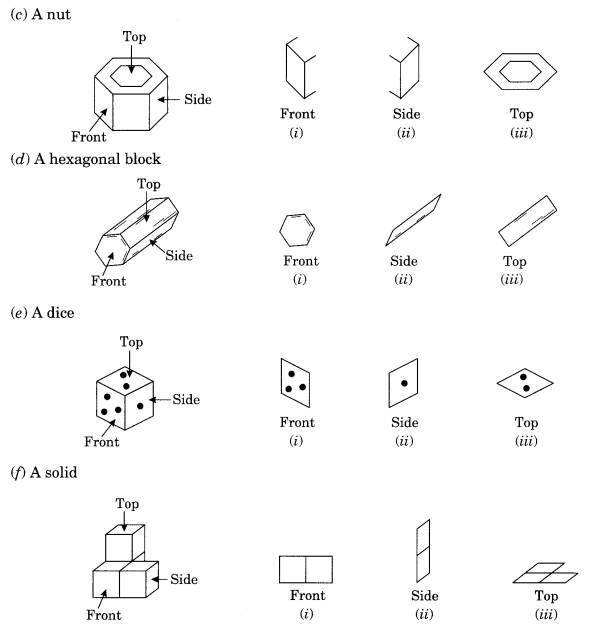
Ex 10.2
प्रश्न 1.
किसी शहर के दिए गए मानचित्र को देखें।
निम्नलिखित के उत्तर दें।
(a) मानचित्र को इस प्रकार रंगें: नीला-पानी, लाल-फायर स्टेशन, नारंगी-लाइब्रेरी, पीला-स्कूल। हरा-पार्क, गुलाबी-कॉलेज, बैंगनी-अस्पताल, भूरा-कब्रिस्तान।
(b) रोड 'C' और नेहरू रोड के चौराहे पर हरा 'X' और गांधी रोड और रोड A के चौराहे पर हरा 'Y' निशान लगाएं।
(c) लाल रंग से लाइब्रेरी से बस डिपो तक एक छोटा सड़क मार्ग बनाएं।
(d) पूर्व में कौन सा है, सिटी पार्क या बाजार?
(e) दक्षिण में कौन सा है, प्राइमरी स्कूल या सीनियर सेकेंडरी स्कूल?
उत्तर:
आवश्यक दिशा के अनुसार छायांकित (रंगीन) मानचित्र भाग (a) में दिया गया है। यहां विभिन्न रंग निम्नानुसार हैं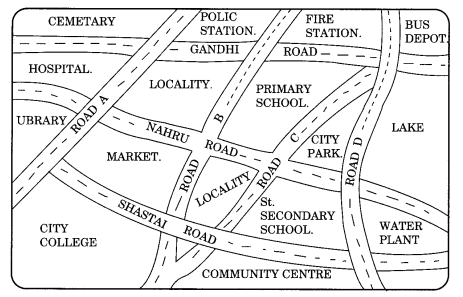
(a) निर्देशानुसार करें
(b) निर्देशानुसार करें
(c) निर्देशानुसार करें
(d) सिटी पार्क
(e) सीनियर सेकेंडरी स्कूल
प्रश्न 2.
विभिन्न वस्तुओं के लिए उचित पैमाने और चिह्नों का प्रयोग करते हुए अपनी कक्षा का एक मानचित्र बनाइए।
उत्तर:
यह एक गतिविधि है, इसलिए इसे स्वयं कीजिए।
प्रश्न 3.
अपने विद्यालय परिसर का एक नक्शा बनाइए, जिसमें खेल के मैदान, मुख्य भवन, बगीचे आदि जैसी विभिन्न विशेषताओं के लिए उचित पैमाने और चिह्नों का प्रयोग किया गया हो।
उत्तर:
यह एक गतिविधि है। कृपया इसे स्वयं करें।
प्रश्न 4.
अपनी सहेली को निर्देश देते हुए एक नक्शा बनाएँ ताकि वह बिना किसी परेशानी के आपके घर पहुँच सके।
उत्तर:
यह एक गतिविधि है। कृपया इसे स्वयं करें।
फलक, किनारे और शीर्ष
नोट:
I. बहुभुज केवल रेखाखंडों से बनी एक 2-D आकृति है।
II. बहुफलक समतल फलकों से बनी एक 3-D आकृति है।
III. बहुफलक का बहुवचन बहुफलक है।
IV. घन, घनाभ, पिरामिड, प्रिज्म आदि बहुफलक हैं जबकि गोले, शंकु और बेलन बहुफलक नहीं हैं।
एक घनाभ में 6 फलक, 12 किनारे और 8 शीर्ष होते हैं।
उत्तल बहुफलक: आपको उत्तल बहुभुजों की अवधारणा याद होगी। उत्तल बहुफलक का विचार भी कुछ ऐसा ही है।
नियमित बहुफलक: एक उत्तल बहुफलक को नियमित कहा जाता है यदि इसके फलक नियमित बहुभुजों से बने होते हैं और प्रत्येक शीर्ष पर समान संख्या में फलक मिलते हैं।
प्रिज्म: प्रिज्म बहुफलक होते हैं जिनके पार्श्व आधार और शीर्ष सर्वांगसम बहुभुज होते हैं तथा अन्य फलक समांतर चतुर्भुज होते हैं।
पिरामिड: पिरामिड बहुफलक होते हैं जिनका आधार बहुभुज होता है तथा जिनके पार्श्व फलक एक उभयनिष्ठ शीर्ष पर त्रिभुज के आकार के होते हैं।
नोट: प्रिज्म या पिरामिड का नाम उसके आधार के नाम पर रखा गया है।
यूलर का सूत्र: यह बहुफलक के फलकों, किनारों और शीर्षों के बीच का संबंध है। इसे
F + V = E + 2 =
F + V – E = 2 द्वारा व्यक्त किया जाता है,
जहाँ F → फलकों की संख्या
V → शीर्षों की संख्या
E → किनारों की संख्या।
Ex 10.3
क्या एक बहुफलक के फलकों में
(i) 3 त्रिभुज हो सकते हैं?
(ii) 4 त्रिभुज हो सकते हैं?
(iii) एक वर्ग और चार त्रिभुज हो सकते हैं?
हल:
(i) नहीं, क्योंकि बहुफलक के किनारे शीर्षों पर मिलते होंगे जो बिंदु हैं।
(ii) हाँ, क्योंकि सभी किनारे शीर्षों पर मिल रहे हैं।
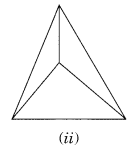
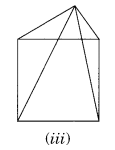
(iii) हाँ, क्योंकि सभी आठ किनारे शीर्षों पर मिलते हैं।
प्रश्न 2.
क्या किसी भी संख्या में फलकों वाला बहुफलक बनाना संभव है?
(संकेत: एक पिरामिड के बारे में सोचें)
हल: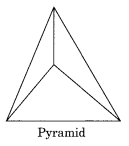
हाँ, यह संभव है यदि फलकों की संख्या 4 से अधिक या उसके बराबर हो।
उदाहरण: पिरामिड जिसमें 4 फलक हों।
प्रश्न 3.
निम्नलिखित में से कौन-से प्रिज्म हैं?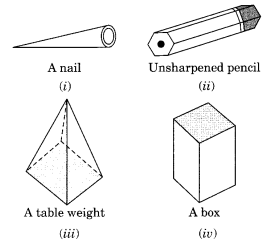
हल:
केवल (ii) बिना नुकीली पेंसिल और (iv) एक डिब्बा प्रिज्म हैं।
प्रश्न 4.
(i) प्रिज्म और बेलन एक जैसे कैसे होते हैं?
(ii) पिरामिड और शंकु एक जैसे कैसे होते हैं?
हल:
(i) यदि किसी प्रिज्म में भुजाओं की संख्या एक निश्चित सीमा तक बढ़ा दी जाए, तो प्रिज्म बेलन का आकार ले लेगा।
(ii) यदि पिरामिड की भुजाओं की संख्या समान सीमा तक बढ़ा दी जाए, तो पिरामिड एक शंकु बन जाता है।
प्रश्न 5.
क्या वर्ग प्रिज्म घन के समान होता है? समझाइए।
हल:
प्रत्येक वर्ग प्रिज्म घन नहीं हो सकता। यह घनाभ भी हो सकता है।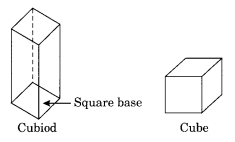
प्रश्न 6.
इन ठोसों के लिए यूलर के सूत्र का सत्यापन कीजिए।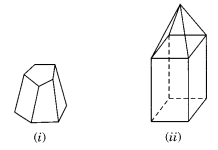
हल:
(i) फलक = 7
भुजाएँ = 15
शीर्ष = 10
यूलर का सूत्र: F + V – E = 2
⇒ 7 + 10 – 15 = 2
⇒ 2 = 2
अतः, यूलर का सूत्र सत्यापित है।
(ii) फलक = 9
भुजाएँ = 16
शीर्ष = 9
यूलर का सूत्र: F + V – E = 2
⇒ 9 + 9 – 16 = 2
⇒ 2 = 2
अतः, यूलर का सूत्र सत्यापित है।
प्रश्न 7.
यूलर के सूत्र का उपयोग करके अज्ञात मान ज्ञात कीजिए।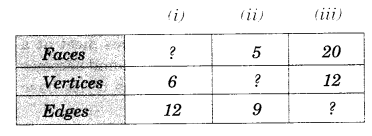
उत्तर:
(i) यहाँ V = 6 और E = 12
F + V – E = 2
F + 6 – 12 = 2
F – 6 = 2
F = 6 + 2 = 8
(ii) F = 5, E = 9
F + V – E = 2
5 + V – 9 = 2
V – 4 = 2
V = 2 + 4 = 6
(iii) यहाँ F = 20 V = 12
F + V – E = 2
20 + 12 – E = 2
32 – E = 2
32 – 2 = E
30 = E
प्रश्न 8.
क्या एक बहुफलक में 10 फलक, 20 किनारे और 15 शीर्ष हो सकते हैं?
उत्तर:
यहाँ, F = 10, E = 20, V = 15
हम जानते हैं कि F + V – E = 2
यहाँ, F + V – E = 10 + 15 – 20
= 25 – 20
= 15 ≠ 2
∴ ऐसा बहुफलक संभव नहीं है।
