SikhLo - Current Affairs in Hindi, Daily current affairs, Current affairs

 NCERT Class 8 Maths Chapter 11 क्षेत्रमिति

NCERT Solutions for Class 8 Maths Chapter 11 क्षेत्रमिति

Ex 11.1

प्रश्न 1.
आकृति में दिए गए मापों वाले एक वर्गाकार और एक आयताकार मैदान का परिमाप समान है। किस मैदान का क्षेत्रफल बड़ा है?
हल:
आकृति (a) का परिमाप = 4 × भुजा = 4 × 60 = 240 मीटर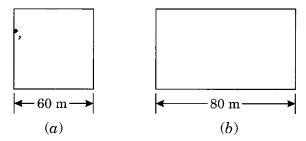

आकृति (b) का परिमाप = 2 [l + b]
आकृति (b) का परिमाप = आकृति (a) का परिमाप
2[l + b] = 240
⇒ 2 [80 + b] = 240
⇒ 80 + b = 120
⇒ b = 120 – 80 = 40 मीटर
आकृति (a) का क्षेत्रफल = (भुजा) 2 = 60 × 60 = 3600 मीटर 2
आकृति (b) का क्षेत्रफल = l × b = 80 × 40 = 3200 मीटर 2
इसलिए, आकृति (a) का क्षेत्रफल आकृति (b) के क्षेत्रफल से लंबा है।

प्रश्न 2.
श्रीमती कौशिक के पास एक वर्गाकार प्लॉट है जिसका माप चित्र में दर्शाया गया है। वह प्लॉट के बीच में एक घर बनाना चाहती हैं। घर के चारों ओर एक बगीचा विकसित किया गया है। ₹ 55 प्रति वर्ग मीटर की दर से घर के चारों ओर बगीचा विकसित करने की कुल लागत ज्ञात कीजिए। हल :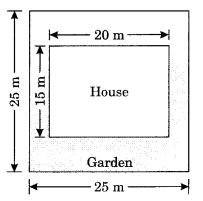

प्लॉट
का क्षेत्रफल = भुजा × भुजा = 25 मीटर × 25 मीटर = 625 मीटर 2
घर का क्षेत्रफल = l × b = 20 मीटर × 15 मीटर = 300 मीटर 2
विकसित किए जाने वाले बगीचे का क्षेत्रफल = प्लॉट का क्षेत्रफल - घर का क्षेत्रफल = 625 मीटर 2 - 300 मीटर 2 = 325 मीटर 2
बगीचा विकसित करने की लागत = ₹ 325 × 55 = ₹ 17875

प्रश्न 3.
एक बगीचे का आकार बीच में आयताकार और सिरों पर अर्धवृत्ताकार है, जैसा कि चित्र में दिखाया गया है। इस बगीचे का क्षेत्रफल और परिमाप ज्ञात कीजिए।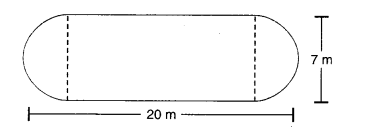

हल:

प्रश्न 4.
एक फर्श टाइल एक समांतर चतुर्भुज के आकार की है जिसका आधार 24 सेमी और संगत ऊँचाई 10 सेमी है। 1080 वर्ग मीटर क्षेत्रफल वाले फर्श को ढकने के लिए ऐसी कितनी टाइलों की आवश्यकता होगी ? (यदि आवश्यक हो, तो आप कोनों को भरने के लिए टाइलों को किसी भी तरह से तोड़ सकते हैं)।
हल:
फर्श का क्षेत्रफल = 1080 वर्ग मीटर = 1080 × 10000 cm2 = 10800000 cm2  [ ∵ 1 वर्ग मीटर = 10000 वर्ग मीटर ] 1

टाइल का क्षेत्रफल = 1 × आधार × ऊँचाई = 1 × 24 × 10 = 240 वर्ग मीटर आवश्यक
टाइलों की संख्या

= 45000 टाइलें

प्रश्न 5.
एक चींटी ज़मीन पर बिखरे हुए अलग-अलग आकार के कुछ खाने के टुकड़ों के चारों ओर घूम रही है। किस खाने के टुकड़े के लिए चींटी को ज़्यादा लंबा चक्कर लगाना पड़ेगा? याद रखें, वृत्त की परिधि c = 2πr के व्यंजक का उपयोग करके प्राप्त की जा सकती है, जहाँ r वृत्त की त्रिज्या है।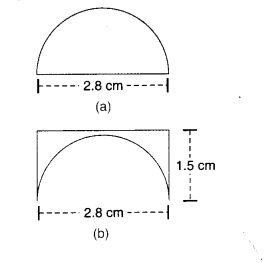


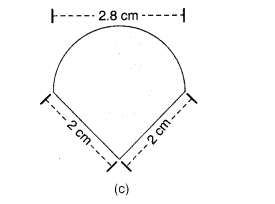
हल:

Ex 11.2

प्रश्न 1.
एक मेज की ऊपरी सतह समलम्ब चतुर्भुज के आकार की है। यदि इसकी समांतर भुजाएँ 1 मीटर और 1.2 मीटर हैं और उनके बीच लंबवत दूरी 0.8 मीटर है, तो इसका क्षेत्रफल ज्ञात कीजिए।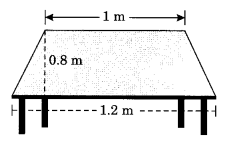

उत्तर:
यहाँ, = a = 1.2mb = 1 मीटर और h = 0.8 मीटर
समलम्ब चतुर्भुज का क्षेत्रफल = 12 × h × (a + b)
= 12 × 0.8 × (1.2 + 1)m 2 = 0.4 × 2.2 = 0.88 m 2

प्रश्न 2.
समलम्ब चतुर्भुज का क्षेत्रफल 34 सेमी 2 है और समानांतर भुजाओं में से एक की लंबाई 10 सेमी और ऊँचाई 4 सेमी है। दूसरी समानांतर भुजा की लंबाई ज्ञात कीजिए।
उत्तर:
माना कि दूसरी समानांतर भुजा की लंबाई 'X' है, समलम्ब चतुर्भुज की ऊँचाई = 4 मीटर। एक समानांतर भुजा की लंबाई = 10 सेमी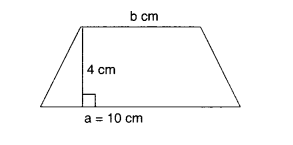

समलम्ब चतुर्भुज का क्षेत्रफल = 34 सेमी 2
12 × h × (a + b) = 34
12 × 4 × (10 + x) = 34
2 (10 + x) = 34
20 + 2x = 34
2x = 34 – 20
2x = 14
x = 142 = 7 सेमी
अतः, दूसरी भुजा की लंबाई = 7 सेमी

प्रश्न 3.
एक समलम्ब चतुर्भुज ABCD के बाड़ की लंबाई 120 मीटर है। यदि BC = 48 मीटर, CD = 17 मीटर और AD = 40 मीटर है, तो इस मैदान का क्षेत्रफल ज्ञात कीजिए। भुजा AB, समांतर भुजाओं AD और BC पर लंबवत है।

उत्तर:
दिया गया है: BC = 48 मीटर, CD = 17 मीटर और AD = 40 मीटर।
समलम्ब चतुर्भुज का परिमाप = 120 मीटर।
AB + BC + CD + DA = 120
AB + 48 + 17 + 40 = 120
AB + 10° = 120
AB = 120 – 10° = 15 मीटर।
AB समलम्ब चतुर्भुज की ऊँचाई है।
समलम्ब चतुर्भुज का क्षेत्रफल = \(\frac{1}{2}\) × h × (a + b) = \(\frac{1}{2}\) × 15 × (48 + 40) m 2 = \(\frac{1}{2}\) × 15 × 88 m 2 = 15 × 44 m 2 = 660 m 2 दिए गए समलम्ब चतुर्भुज का क्षेत्रफल = 660 m 212× एच × (ए + बी)
12× 15 × (48 + 40) मीटर
12× 15 × 88 मीटर

प्रश्न 4.
एक चतुर्भुजाकार खेत का विकर्ण 24 मीटर है और शेष सम्मुख शीर्षों से इस पर डाले गए लंब क्रमशः 8 मीटर और 13 मीटर हैं। खेत का क्षेत्रफल ज्ञात कीजिए।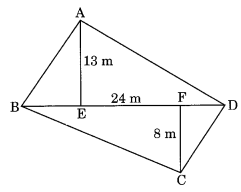

उत्तर:
दिए गए चतुर्भुज में, d = 24 मीटर, h = 13 मीटर और h = 8 मीटर है। 
चतुर्भुज का क्षेत्रफल = \(\frac{1}{2}\) × d × (h12× d × (h 1 + h 2 )
= \(\frac{1}{2}\) × 24 × (13 + 8) मी12× 24 × (13 + 8) मी 2
= 12 × 21 मी 2 = 252 मी 2

प्रश्न 5.
एक समचतुर्भुज के विकर्ण 7.5 सेमी और 12 सेमी हैं। इसका क्षेत्रफल ज्ञात कीजिए।
उत्तर:
यहाँ d 1 = 7.5 सेमी, d 2 = 12 सेमी
समचतुर्भुज का क्षेत्रफल = \(\frac{1}{2}\) × d12× d 1 × d 2
= \(\frac{1}{2}\) × 7.5 × 12 सेमी12× 7.5 × 12 सेमी 2 = 7.5 × 6 सेमी 2 = 45 सेमी 2

प्रश्न 6.
एक समचतुर्भुज का क्षेत्रफल ज्ञात कीजिए जिसकी भुजा 5 सेमी और ऊँचाई 4.8 सेमी है। यदि इसका एक विकर्ण 8 सेमी लंबा है, तो दूसरे विकर्ण की लंबाई ज्ञात कीजिए।
उत्तर
हम जानते हैं कि समचतुर्भुज एक समांतर चतुर्भुज भी है।
समचतुर्भुज का क्षेत्रफल = समांतर चतुर्भुज का क्षेत्रफल = bh = 5 × 4.8 सेमी 2 × = 24 सेमी 2
मान लीजिए कि दूसरा विकर्ण 'x' है।
समचतुर्भुज का क्षेत्रफल = 24 सेमी 2
\(\frac{1}{2}\) × d12× d 1 × d 2 = 24
\(\frac{1}{2}\) × 8 × x = 2412× 8 × x = 24
4 × x = 24
x = \(\frac{24}{4}\) = 6 सेमी244= 6 सेमी
∴ अभीष्ट विकर्ण = 6 सेमी

प्रश्न 7.
एक ऊँचे चबूतरे का ऊपरी पृष्ठ एक सम अष्टकोण के आकार का है जैसा कि चित्र में दिखाया गया है। अष्टकोणीय पृष्ठ का क्षेत्रफल ज्ञात कीजिए।
हल:
अष्टकोणीय पृष्ठ का क्षेत्रफल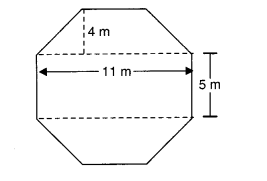

प्रश्न 8.
आकृति में दर्शाए अनुसार एक पंचकोणीय पार्क है। इसका क्षेत्रफल ज्ञात करने के लिए ज्योति और कविता ने इसे दो अलग-अलग तरीकों से विभाजित किया।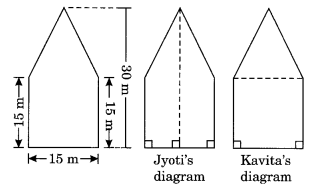

दोनों तरीकों का उपयोग करके इस पार्क का क्षेत्रफल ज्ञात कीजिए। क्या आप इसका क्षेत्रफल ज्ञात करने का कोई अन्य तरीका सुझा सकते हैं?
हल:
(i) ज्योति के आरेख से: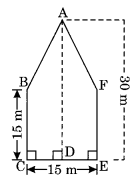

पंचकोणीय आकार का क्षेत्रफल = समलम्ब चतुर्भुज ABCD का क्षेत्रफल + समलम्ब चतुर्भुज ADEF का क्षेत्रफल
= 2 × समलम्ब चतुर्भुज ABCD का क्षेत्रफल
= 2 ×12(a + b) × h
= (15 + 30) × 7.5
= 45 × 7.5
= 337.5 मी 2
(ii) कविता के आरेख से: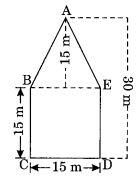

पंचकोणीय आकार का क्षेत्रफल = ∆ABE का क्षेत्रफल + वर्ग BCDE का क्षेत्रफल
=12× बी × एच + 15 × 15
=12× 15 × 15 + 225
= 112.5 + 225
= 337.5 वर्ग मीटर हाँ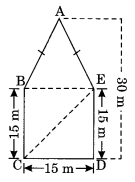

, हम दी गई पंचकोणीय आकृति का क्षेत्रफल ज्ञात करने का दूसरा तरीका भी खोज सकते हैं।
आकृति को दो भागों, अर्थात् समलम्ब चतुर्भुज ABCE और समकोण त्रिभुज EDC, में विभाजित करने के लिए CE को मिलाएँ।
ABCDE का क्षेत्रफल = ∆EDC का क्षेत्रफल + वर्ग ABCE का क्षेत्रफल

प्रश्न 9.
चित्र फ़्रेम के आरेख की बाहरी विमाएँ = 24 सेमी × 28 सेमी और आंतरिक विमाएँ 16 सेमी × 20 सेमी हैं। फ़्रेम के प्रत्येक भाग का क्षेत्रफल ज्ञात कीजिए, यदि प्रत्येक भाग की चौड़ाई समान है।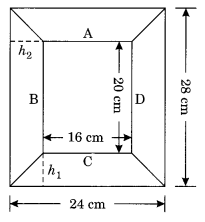

हल:

अतः, चार भागों A, B, C और D के क्षेत्रफल क्रमशः 80 सेमी 2 , 96 सेमी 2 , 80 सेमी 2 और 96 सेमी 2 हैं।

Ex 11.3

प्रश्न 1.
आकृति में दिखाए अनुसार दो घनाभाकार डिब्बे हैं। किस डिब्बे को बनाने में कम सामग्री की आवश्यकता है?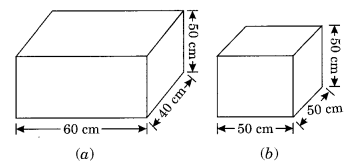

हल:
(a) घनाभ का आयतन = l × b × h = 60 × 40 × 50 = 120000 cm 3
(b) घन का आयतन = (भुजा) 3 = (50) 3 = 50 × 50 × 50 = 125000 cm 3
घनाभाकार डिब्बे (a) को बनाने में कम सामग्री की आवश्यकता होती है।

प्रश्न 2.
80 सेमी × 48 सेमी × 24 सेमी माप वाले एक सूटकेस को तिरपाल से ढकना है। ऐसे 100 सूटकेसों को ढकने के लिए 96 सेमी चौड़ाई वाले कितने मीटर तिरपाल की आवश्यकता होगी?
समाधान:
सूटकेस का माप = 80 सेमी × 48 सेमी × 24 सेमी
l = 80 सेमी, b = 48 सेमी और h = 24 सेमी
सूटकेस का कुल सतह क्षेत्र = 2 [lb + bh + hl]
= 2 [80 × 48 + 48 × 24 + 24 × 80]
= 2 [3840 + 1152 + 1920]
= 2 × 6912
= 13824 सेमी 2
तिरपाल का क्षेत्रफल = लंबाई × चौड़ाई = l × 96 = 96l सेमी 2
तिरपाल का क्षेत्रफल = 100 सूटकेस का क्षेत्रफल
96l = 100 × 13824
l = 100 × 144 = 14400 सेमी = 144 मीटर
इसलिए, कपड़े की आवश्यक लंबाई = 144 मीटर।

प्रश्न 3.
उस घन की भुजा ज्ञात कीजिए जिसका पृष्ठीय क्षेत्रफल 600 सेमी 2 है ?
हल:
घन का कुल पृष्ठीय क्षेत्रफल = 6l 2
6l 2 = 600
l 2 = 100
l = √100 = 10 सेमी
अतः, भुजा की अभीष्ट लंबाई = 10 सेमी.

प्रश्न 4.
रुखसार ने 1 मीटर × 2 मीटर × 1.5 मीटर माप वाले कैबिनेट के बाहरी हिस्से को रंगा। यदि उसने कैबिनेट के निचले हिस्से को छोड़कर बाकी सभी हिस्सों को रंगा तो उसने कितना पृष्ठीय क्षेत्रफल कवर किया?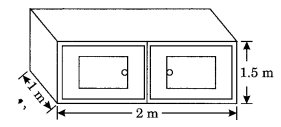

हल:
l = 2 मीटर, b = 1.5 मीटर, h = 1 मीटर
रंगे जाने वाले पृष्ठ का क्षेत्रफल = बॉक्स का कुल पृष्ठीय क्षेत्रफल - बॉक्स के आधार का क्षेत्रफल
= 2 [lb + bh + hl] - lb
= 2[2 × 1.5 + 1.5 × 1 + 1 × 2] - 2 × 1 =
2[3 + 1.5 + 2] - 2
= 2[6.5] - 2
= 13 - 2
= 11 मीटर 2
इसलिए, अभीष्ट क्षेत्रफल = 11 मीटर 2

प्रश्न 5.
डैनियल एक घनाभाकार हॉल की दीवारों और छत को पेंट कर रही है, जिसकी लंबाई, चौड़ाई और ऊँचाई क्रमशः 15 मीटर, 10 मीटर और 7 मीटर है। पेंट के प्रत्येक डिब्बे से 100 m2 क्षेत्रफल पेंट किया जाता है।
कमरे को पेंट करने के लिए उसे कितने डिब्बों पेंट की आवश्यकता होगी?
हल:
l = 15 मीटर
b = 10 मीटर
h = 7 मीटर
पेंट किया जाने वाला पृष्ठीय क्षेत्रफल

अतः, कमरे को पेंट करने के लिए उसे 5 डिब्बों पेंट की आवश्यकता होगी।

प्रश्न 6.
बताइए कि दाईं ओर की दो आकृतियाँ किस प्रकार एक जैसी हैं और किस प्रकार भिन्न हैं। किस डिब्बे का पार्श्व पृष्ठीय क्षेत्रफल बड़ा है?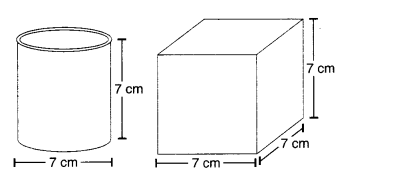

हल:
समानता → दोनों की ऊँचाई समान है।
अंतर → एक बेलन है, दूसरा घन है;
बेलन एक ठोस है जो अपनी एक भुजा के चारों ओर एक आयताकार क्षेत्र को घुमाकर प्राप्त किया जाता है, जबकि घन छह वर्गाकार फलकों से घिरा एक ठोस होता है; बेलन के दो गोलाकार फलक होते हैं जबकि घन के छह वर्गाकार फलक होते हैं।

प्रश्न 7.
7 मीटर त्रिज्या और 3 मीटर ऊँचाई वाला एक बंद बेलनाकार टैंक धातु की एक शीट से बना है। इसके लिए कितनी धातु की शीटों की आवश्यकता होगी?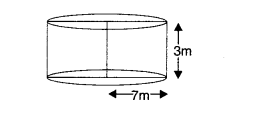

हल: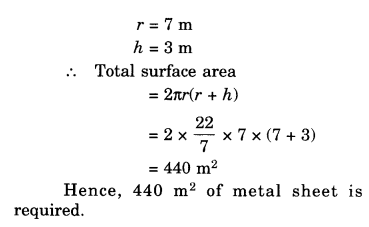

प्रश्न 8.
एक खोखले बेलन का पार्श्व पृष्ठीय क्षेत्रफल 4224 सेमी 2 है । इसे इसकी ऊँचाई के अनुदिश काटकर 33 सेमी चौड़ाई की एक आयताकार शीट बनाई गई है। आयताकार शीट का परिमाप ज्ञात कीजिए।
हल:
आयताकार शीट की चौड़ाई = बेलन की परिधि

h = 128 सेमी
l = 128 सेमी, b = 33 सेमी
शीट का परिमाप = 2(l + b) = 2(128 + 33) = 2 × 161 = 322 सेमी
अतः, अभीष्ट परिमाप = 322 सेमी

प्रश्न 9.
एक रोड रोलर एक सड़क को समतल करने के लिए एक बार चलने में 750 पूर्ण चक्कर लगाता है। यदि रोड रोलर का व्यास 84 सेमी और लंबाई 1 मीटर है, तो सड़क का क्षेत्रफल ज्ञात कीजिए।

हल:
रोड रोलर का पार्श्व पृष्ठीय क्षेत्रफल = 2πrh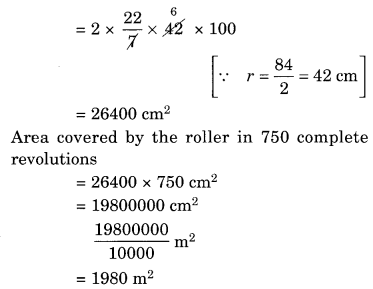

अतः, सड़क का क्षेत्रफल = 1980 वर्ग मीटर

प्रश्न 10.
एक कंपनी अपने दूध पाउडर को एक बेलनाकार कंटेनर में पैक करती है जिसका आधार व्यास 14 सेमी और ऊँचाई 20 सेमी है। कंपनी कंटेनर की सतह के चारों ओर एक लेबल लगाती है (जैसा कि चित्र में दिखाया गया है)। यदि लेबल ऊपर और नीचे से 2 सेमी की दूरी पर रखा जाता है, तो लेबल का क्षेत्रफल क्या है?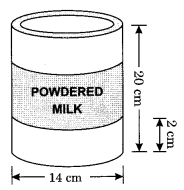

हल:
यहाँ, r = \(\frac { 14 }{ 2 }\) = 7 सेमी142
बेलनाकार लेबल की ऊँचाई = 20 – (2 + 2) = 16 सेमी
बेलनाकार लेबल का पृष्ठीय क्षेत्रफल = 2πrh
= 2 × \(\frac { 22 }{ 7 }\) × 7 × 16227
= 704 सेमी 2
अतः लेबल का आवश्यक क्षेत्रफल = 704 सेमी 2 है।

Ex 11.4

प्रश्न 1.
एक बेलनाकार टैंक दिया गया है, किस स्थिति में आप इसका पृष्ठीय क्षेत्रफल और किस स्थिति में आयतन ज्ञात करेंगे?

(a) यह ज्ञात करने के लिए कि इसमें कितना पानी आ सकता है?
(b) इसे प्लास्टर करने के लिए आवश्यक सीमेंट की बोरियों की संख्या?
(c) इससे भरे जा सकने वाले छोटे टैंकों की संख्या ज्ञात करने के लिए।
हल:
(a) इस स्थिति में, हम इसका आयतन ज्ञात कर सकते हैं।
(b) इस स्थिति में, हम इसका पृष्ठीय क्षेत्रफल ज्ञात कर सकते हैं।
(c) इस स्थिति में, हम इसका आयतन ज्ञात कर सकते हैं।

प्रश्न 2.
बेलन A का व्यास 7 सेमी और ऊँचाई 14 सेमी है। बेलन B का व्यास 14 सेमी और ऊँचाई 7 सेमी है। बिना कोई गणना किए, क्या आप बता सकते हैं कि किसका आयतन ज़्यादा है? दोनों बेलनों का आयतन ज्ञात करके इसकी पुष्टि कीजिए। जाँच कीजिए कि क्या ज़्यादा आयतन वाले बेलन का पृष्ठीय क्षेत्रफल भी ज़्यादा है?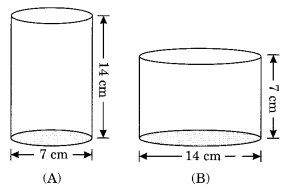

हल:
बेलन B का आयतन ज़्यादा है।
सत्यापन:
बेलन A का आयतन = πr 2 h

प्रश्न 3.
एक घनाभ की ऊँचाई ज्ञात कीजिए जिसके आधार का क्षेत्रफल 180 सेमी 2 और आयतन 900 सेमी 3 है ।
हल:
दिया गया है: आधार का क्षेत्रफल = lb = 180 सेमी 2
V = 900 सेमी 3
घनाभ का आयतन = l × b × h
900 = 180 × h
h = 5 सेमी
इसलिए, आवश्यक ऊँचाई = 5 सेमी।

प्रश्न 4.
एक घनाभ की विमाएँ 60 सेमी × 54 सेमी × 30 सेमी हैं। दिए गए घनाभ में 6 सेमी भुजा वाले कितने छोटे घन रखे जा सकते हैं?
हल:
घनाभ का आयतन = ल × चौ × ऊँचाई = 60 सेमी × 54 सेमी × 30 सेमी = 97200 सेमी 3
घन का आयतन = (भुजा) 3 = (6) 3 = 216 सेमी 3
घनाभ से घनों की संख्या

अतः, घनों की आवश्यक संख्या = 450

प्रश्न 5.
उस बेलन की ऊँचाई ज्ञात कीजिए जिसका आयतन 1.54 m 3 है और आधार का व्यास 140 cm है।
हल:
V = 1.54 m 3 , d = 140 cm = 1.40 m
बेलन का आयतन = πr2h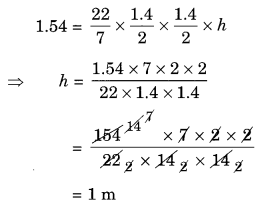

अतः, बेलन की ऊँचाई = 1 m है।

प्रश्न 6.
एक दूध की टंकी बेलन के आकार की है जिसकी त्रिज्या 1.5 मीटर और लंबाई 7 मीटर है। इस टंकी में संग्रहित किए जा सकने वाले दूध की मात्रा लीटर में ज्ञात कीजिए।
हल: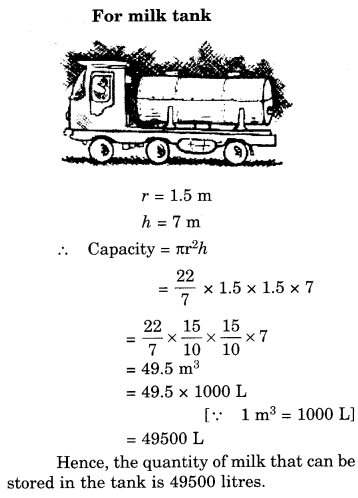

प्रश्न 7.
यदि किसी घन के प्रत्येक किनारे को दोगुना कर दिया जाए, तो
(i) इसका पृष्ठीय क्षेत्रफल कितने गुना बढ़ जाएगा?
(ii) इसका आयतन कितने गुना बढ़ जाएगा?
हल:
माना घन का किनारा = x सेमी
यदि किनारे को दोगुना कर दिया जाए, तो नया किनारा = 2x सेमी
(i) मूल पृष्ठीय क्षेत्रफल = 6x 2 सेमी 2
नया पृष्ठीय क्षेत्रफल = 6(2x) 2 = 6 × 4x 2 = 24x 2
अनुपात = 6x 2 : 24x 2 = 1 : 4
अतः, नया पृष्ठीय क्षेत्रफल मूल पृष्ठीय क्षेत्रफल का चार गुना होगा।

(ii) घन का मूल आयतन = x 3 सेमी 3
घन का नया आयतन = (2x) 3 = 8x 3 सेमी 3
अनुपात = x 3 : 8x 3 = 1: 8
अतः, नया आयतन मूल आयतन का आठ गुना होगा।

प्रश्न 8.
एक घनाभाकार कुंड में 60 लीटर प्रति मिनट की दर से पानी डाला जा रहा है। यदि कुंड का आयतन 108 m3 है , तो कुंड को भरने में लगने वाले घंटों की संख्या ज्ञात कीजिए।
हल:
कुंड का आयतन = 108 m3 = 108000 L [∵1 m3 = 1000 L]
1 मिनट में कुंड में बहने वाले पानी का आयतन = 60 L
कुंड को भरने में लगा समय

अतः कुंड को भरने में लगने वाले घंटे = 30 घंटे।