SikhLo - Current Affairs in Hindi, Daily current affairs, Current affairs

 NCERT Class 8 Maths Chapter 9 बीजीय व्यंजक एवं सर्वसमिकाएँ

NCERT Solutions for Class 8 Maths Chapter 9 बीजीय व्यंजक एवं सर्वसमिकाएँ

Ex 9.1

प्रश्न 1.
निम्नलिखित प्रत्येक व्यंजक के लिए पदों और उनके गुणांकों की पहचान कीजिए।
(i) 5xyz 2 – 3zy
(ii) 1 + x + x 2
(iii) 4x 2 y 2 – 4x 2 y 2 z 2 + z 2
(iv) 3 – pq + qr – rp
(v) \(\frac { x }{ 2 }\) + \(\frac { y }{ 2 }\) – xyx2+y2– xy
(vi) 0.3a – 0.6ab + 0.5b
समाधान: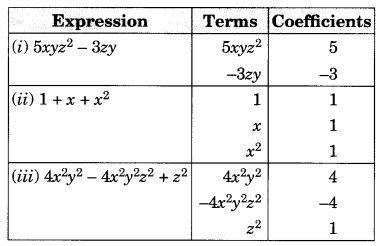

प्रश्न 2.
निम्नलिखित बहुपदों को एकपदी, द्विपद, त्रिपद के रूप में वर्गीकृत करें। कौन से बहुपद इन तीनों श्रेणियों में से किसी में भी फिट नहीं बैठते हैं?
x + y, 1000, x + x 2 + x 3 + x 4 , 7 + y + 5x, 2y – 3y 2 , 2y – 3y 2 + 4y 3 , 5x – 4y + 3xy, 4z – 15z 2 , ab + bc + cd + da, pqr, p 2 q + pq 2 , 2p + 2q
हल:

प्रश्न 3.
निम्नलिखित को जोड़ें:
(i) ab – bc, bc – ca, ca – ab
(ii) a – b + ab, b – c + bc, c – a + ac
(iii) 2p 2 q 2 – 3pq + 4, 5 + 7pq – 3p 2 q 2
(iv) l 2 + m 2 , m 2 + n 2 , n 2 + l 2 , 2lm + 2mn + 2nl
हल:
(i) दिया गया है: ab – bc, bc – ca, ca – ab
हमारे पास है
(ab – bc) + (bc – ca) + (ca – ab) (सभी पदों को जोड़ने पर)
= ab – bc + bc – ca + ca – ab
= (ab – ab) + (bc – bc) + (ca – ca) (समान पदों को एक साथ एकत्रित करने पर)
= 0 + 0 + 0
= 0

(ii) दिया गया है:
a – b + ab, b – c + bc, c – a + ac
हमारे पास है (a – b + ab) + (b – c + bc) + (c – a + ac) (सभी पदों को जोड़ने पर)
= a – b + ab + b – c + bc + c – a + ac
= (a – a) + (b – b) + (c – c) + ab + bc + ac (सभी समान पदों को एक साथ एकत्रित करने पर)
= 0 + 0 + 0 + ab + bc + ac
= ab + bc + ac

(iii) दिया गया है:
2p 2 q 2 – 3pq + 4, 5 + 7pq – 3p 2 q 2
समान पदों को एक ही कॉलम में व्यवस्थित करने पर, हमें प्राप्त होता है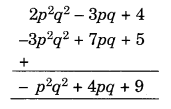

(कॉलमवार जोड़ने पर)

(iv) दिया गया है: l 2 + m 2 , m 2 + n 2 , n 2 + l 2 , 2lm + 2mn + nl
समान पदों को एक ही कॉलम में व्यवस्थित करने पर, हमें प्राप्त होता है

इस प्रकार, दिए गए व्यंजकों का योग 2(l 2 + m 2 + n 2  + lm + mn + nl) है

प्रश्न 4.
(a) 12a – 9ab + 5b – 3 में से 4a – 7ab + 3b + 12 घटाएँ
(6) 5xy – 2yz – 2zx + 10xyz में से 3xy + 5yz – 7zx
घटाएँ (c) 18 – 3p – 11q + 5pq – 2pq 2 + 5p 2 q में से 4p 2 q – 3pq + 5pq 2 – 8p + 7q – 10 घटाएँ हल: (a) समान पदों को स्तंभ-वार व्यवस्थित करने पर, हमारे पास है [निचले व्यंजकों के सभी पदों के चिह्न बदलें और फिर जोड़ें] (b) समान पदों को स्तंभ-वार व्यवस्थित करने पर, हमारे पास है [निचले व्यंजकों के सभी पदों के चिह्न बदलें और फिर जोड़ें] (c) समान पदों को स्तंभ-वार व्यवस्थित करने पर, हमारे पास है [सभी के चिह्न बदलें निचले व्यंजकों के पदों को जोड़ें और फिर जोड़ें] पद हैं p 2 q – 7pq 2 + 8pq – 18q + 5p + 20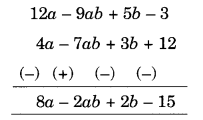

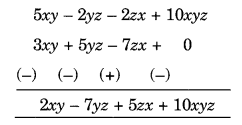
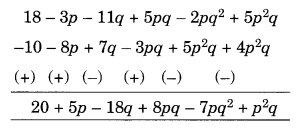
Ex 9.2

प्रश्न 1.
निम्नलिखित एकपदी युग्मों का गुणनफल ज्ञात कीजिए
(i) 4, 7p
(ii) -4p, 7p
(iii) -4p, 7pq
(iv) 4p 3 , – 3p
(v) 4p, 0
हल:
(i) 4 × 7p
= (4 × 7)p
= 28p

(ii) -4p × 7p
= {(-4) × 7} × (p × p)
= (-28) × p 2
= -28p 2

(iii) -4p × 7pq
= {(-4) × 7} × {p × (pq)}
= -28 × (p × p × q)
= -28p 2 q

(iv) 4p 3 × -3p
= {4 × (-3)} × (p 3 × p)
= -12 × (p 4 )
= -12p 4

(v) 4p × 0
= (4 × 0) × p
= 0 × p
= 0

प्रश्न 2.
निम्नलिखित एकपदी युग्मों को क्रमशः उनकी लंबाई और चौड़ाई मानकर आयतों के क्षेत्रफल ज्ञात कीजिए।
(p, q); (10m, 5n); (20x 2 , 5y 2 ); (4x, 3x 2 ); (3mn, 4np)
हल:
(i) (p, q)
आयत का क्षेत्रफल = लंबाई × चौड़ाई
= pxq
= pq

(ii) (10 मी, 5एन)
आयत का क्षेत्रफल = लंबाई × चौड़ाई
= 10 मी × 5एन
= (10 × 5) × (मी × एन)
= 50 × एमएन
= 50 एमएन

(iii) 20x 2 , 5y 2
आयत का क्षेत्रफल = लंबाई × चौड़ाई
= 20x 2 × 5y 2
= (20 × 5) × (x 2 × y 2 )
= 100 × x 2 y 2
= 100x 2 y 2

(iv) (4x, 3x 2 )
आयत का क्षेत्रफल = लंबाई × चौड़ाई
= 4x × 3x 2
= (4 × 3) × (x × x 2 )
= 12 × x 3
= 12x 3

(v) (3mn, 4np)
आयत का क्षेत्रफल = लंबाई × चौड़ाई
= 3mn × 4np
= (3 × 4) × (mn × np)
= 12 × m × (n × n) × p
= 12 × m × n 2 × p
= 12mn 2 p

प्रश्न 3.
गुणनफल की तालिका को पूरा कीजिए।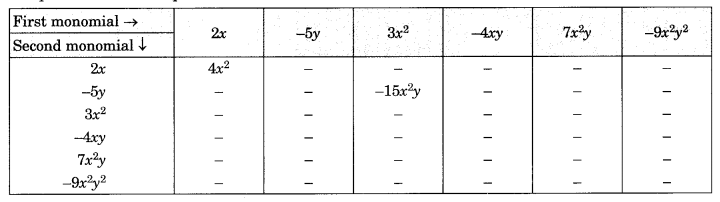

हल:
पूर्ण तालिका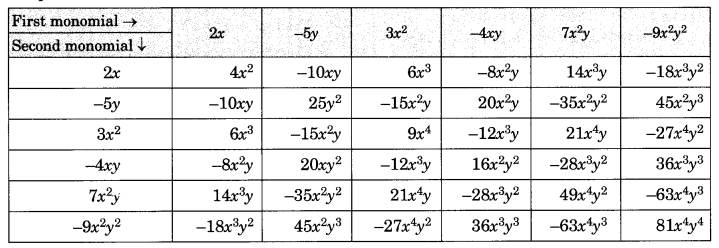

प्रश्न 4.
निम्नलिखित लंबाई, चौड़ाई और ऊँचाई वाले आयताकार बक्सों का आयतन क्रमशः ज्ञात कीजिए।
(i) 5a, 3a 2 , 7a4
(ii) 2p, 4q, 8r
(iii) xy, 2x 2 y, 2xy 2
(iv) a, 2b, 3c
हल:
(i) 5a, 3a 2 , 7a 4
आयताकार बक्से का आयतन = लंबाई × चौड़ाई × ऊँचाई
= (5a) × (3a 2 ) × (7a 4 )
= (5 × 3 × 7) × (a × a 2 × a 4 )
= 105a 7

(ii) 2p, 4q, 8r
आयताकार बॉक्स का आयतन = लंबाई × चौड़ाई × ऊँचाई
= 2p × 4q × 8r
= (2 × 4 × 8) × (p × q × r)
= 64pqr

(iii) xy; 2x 2 y; 2xy 2
आयताकार डिब्बे का आयतन = लंबाई × चौड़ाई × ऊँचाई
= xy × 2x 2 y × 2xy 2
= (1 × 2 × 2) × (x × x 2 × x) × (y × y × y 2 )
= 4 × x 4 × y 4
= 4x 4 y 4

(iv) a, 2b, 3c
आयताकार बॉक्स का आयतन = लंबाई × चौड़ाई × ऊँचाई
= a × 2b × 3c
= (1 × 2 × 3) × (a × b × c)
= 6abc

प्रश्न 5.
गुणनफल ज्ञात कीजिए
(i) xy, yz, zx
(ii) a, -a 2 , a 3
(iii) 2, 4y, 8y 2 , 16y 3
(iv) a, 2b, 3c, 6abc
(v) m, -mn, mnp
हल:
(i) xy × yz × zx = x 2 y 2 z 2
(ii) a × (-a 2 ) × a 3 = -a 6
(iii) 2 × 4y × 8y 2 × 16y 3 = (2 × 4 × 8 × 16) × y × y 2 × y 3 = 1024y 6
(iv) a × 2b × 3c × 6abc = (1 × 2 × 3 × 6) × a × b × c × abc = 36 a 2 b 2 c 2

(v) m × (-mn) × mnp = [1 × (-1) × 1 ]m × mn × mnp = -m 3 n 2 p

Ex 9.3

प्रश्न 1.
निम्नलिखित प्रत्येक युग्म में व्यंजकों का गुणनफल कीजिए।
(i) 4p, q + r
(ii) ab, a – b
(iii) a + b, 7a 2 b 2
(iv) a 2 – 9, 4a
(v) pq + qr + rp, 0
हल:
(i) (4p) × (q + r)
= (4p × q) + (4p × r)
= 4pq + 4pr

(ii) (ab) × (a – b)
= (ab × a) – (ab × b)
= a2b – ab2

(iii) (a + b) (7a2b2)
= (a × 7a2b2) + (b × 7a2b2)
= 7a3b2 + 7a2b3

(iv) (a2 – 9) × 4a
= (a2 × 4a) – (9 × 4a)
= 4a3 – 36a

(v) (pq + qr + rp) × 0
= (pq × 0) + (qr × 0) + (rp × 0)
= 0 + 0 + 0
= 0

प्रश्न 2.
तालिका को पूरा कीजिए।

हल:
(i) a × (b + c + d)
= (a × b) + (a × c) + (a × d)
= ab + ac + ad

(ii) (x + y – 5) (5xy)
= (x × 5xy) + (y × 5xy) – (5 × 5xy)
= 5x 2 y + 5xy 2 – 25xy

(iii) p × (6p 2 – 7p + 5)
= (p × 6p 2 ) + p × (-7p) + p × 5
= 6p 3 + (-7p 2 ) + 5p
= 6p 3 – 7p 2 + 5p

(iv) 4p 2 q 2 × (p 2 – q 2 )
= (4p 2 q 2 × p 2 ) + (4p 2 q 2 × -q 2 )
= 4p 4 q 2 + (-4p 2 q 4 )
= 4p 4 q 2 – 4p 2 q 4

(v) (a + b + c) × abc
= (a × abc) + (b × abc) + (c × abc)
= a 2 bc + ab 2 c + abc 2

प्रश्न 3.
गुणनफल ज्ञात कीजिए।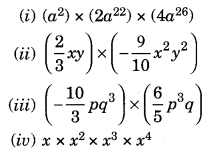

हल: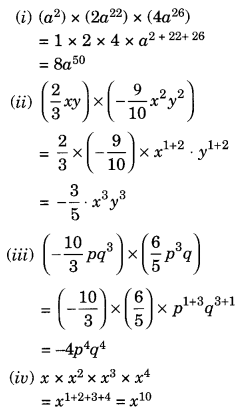

प्रश्न 4.
(a) 3x(4x – 5) + 3 को सरल कीजिए और इसके मान ज्ञात कीजिए:
(i) x = 3
(ii) x =12
(b) a (a 2 + a + 1) + 5 को सरल कीजिए और इसका मान ज्ञात कीजिए:
(i) a = 0
(ii) a = 1
(iii) a = -1.
हल:
(a) 3x (4x – 5) + 3
= (3x × 4x) + (3x × -5) + 3
= 12x 2 – 15x + 3
(i) जब x = 3
12x 2 – 15x + 3
= 12 × (3) 2 – 15(3) + 3
= 12 × 9 – 45 + 3
= 108 – 45 + 3
= 111 – 45
= 66

(ii) जब x =12
12x 2 – 15x + 3

(b) a(a2 + a + 1) + 5
= (a × a2) + (a × a) + (a × 1) + 5
= a3 + a2 + a + 5

(i) जब a = 0
a 3 + a 2 + a + 5
= (0) 3 + (0) 2 + 0 + 5
= 0 + 0 + 0 + 5
= 5

(ii) जब a = 1
a 3 + a 2 + a + 5
= (1 3 ) + (1 2 ) + 1 + 5
= 1 + 1 + 1 + 5
= 8

(iii) जब a = -1
a 3 + a 2 + a + 5
= (-1) 3 + (-1) 2 + (-1) + 5
= (-1) + 1 – 1 + 5
= -1 + 1 – 1 + 5
= 4

प्रश्न 5.
(a) जोड़ें: p(p – q), q(q – r) और r (r – p)
(b) जोड़ें: 2x(z – x – y) और 2y(z – y – x)
(c) घटाएँ: 3l(l – 4m + 5n) को 4l(10n – 3m + 2l) से
(d) घटाएँ: 3a(a + b + c) – 2b(a – b + c) को 4c (-a + b + c) से
हल:
(a) p(p – q) + q(q – r) + r(r – p)
= p × p – p × q + q × q + q(-r) + r × r + r × (-p)
= p 2 – pq + q 2 – qr + r 2 – rp
= p 2 + q 2 + r 2 – (pq + qr + rp)

(b) 2x (z – x – y) + 2y(z – y – x)
= 2x × z + 2x (-x) + 2x (-y) + 2yz + 2y (-y) + 2y(-x)
= 2xz – 2x 2 – 2xy + 2yz – 2y 2 – 2xy
= -2x 2 – 2y 2 – 4xy + 2yz + 2xz

(c) 4l(10n – 3m + 2l) – 3l(l – 4m + 5n)
= (4l × 10n) + (4l × -3m) + (4l × 2l) + (-3l × 1) + (-3l × -4m) + (-3l × 5n)
= 40ln + (-12lm) + 8l2 + (-3l2) + 12lm + (-15ln)
= 40ln – 12lm + 8l2 – 3l2 + 12lm – 15ln
= 40ln – 15ln – 12lm + 12lm + 8l2 – 3l2
= 25ln + 5l2
= 5l2 + 25ln

(d) भाग I को सरल करें, हमें 3a (a + b + c) - 2b(a - b + c)
= (3a × a) + (3a × b) + (3a × c) – [(2b × a) + 2b(-b) + (2b) × c]
= 3a2 + 3ab + 3ac – (2ab – 2b2 + 2bc)
= 3a2 + 3ab + 3ac – 2ab + 2b2 – 2bc
= 3a2 + 2b2 + 3ab – 2ab + 3ac – 2bc
= 3a2 + 2b2 + ab + 3ac – 2bc
Simplify the 2nd part 4c × (-a + b + c) = (4c × – a) + (4c × b) + (4c × c)
According to the given question = -4ac + 4bc + 4c2
2nd part – 1st part
= -4ac + 4bc + 4c2 – (3a2 + 2b2 + ab + 3ac – 2bc)
= -4ac + 4bc + 4c2 – 3a2 – 2b2 – ab – 3ac + 2bc
= -4ac – 3ac + 4bc + 2bc + 4c2 – 3a2 – 2b2 – ab
= -7ac + 6bc + 4c2 – 3a2 – 2b2 – ab
= -3a2 – 2b2 + 4c2 – ab + 6bc – 7ac

Ex 9.4

प्रश्न 1.
द्विपदों को गुणा करें:
(i) (2x + 5) और (4x – 3)
(ii) (y – 8) और (3y – 4)
(iii) (2.5l – 0.5 m) और (2.5l + 0.5m)
(iv) (a + 3b) और (x + 5)
(v) (2pq+3q2)and(3pq−2q2)
(vi) (34a2+3b2)and4(a2−23b2)
समाधान।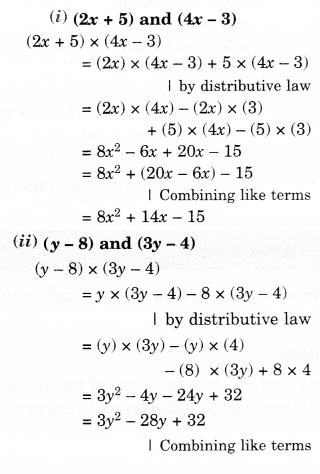

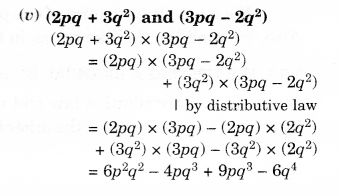
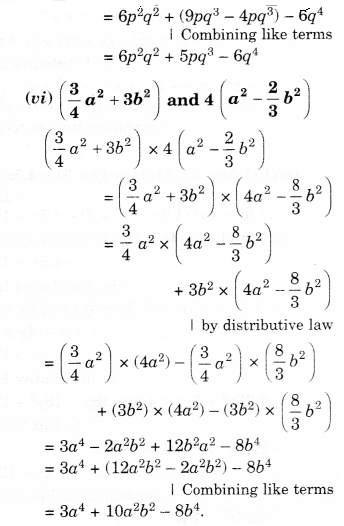
प्रश्न 2.
गुणनफल ज्ञात कीजिए:
(i) (5 – 2x) (3 + x)
(ii) (x + 7y) (7x – y)
(iii) (a 2 + b) (a + b 2 )
(iv) (p 2 – q 2 )(2p + q)
हल:
(i) (5 – 2x) (3 + x)
= 5(3 + x) – 2x(3 + x)
= (5 × 3) + (5 × x) – (2x × 3) – (2x × x)
= 15 + 5x – 6x – 2x 2

(ii) (x + 7y) (7x – y)
= x(7x – y) + 7y(7x – y)
= (x × 7x) – (x × y) + (7y × 7x) – (7y × y)
= 7x 2 – xy + 49xy – 7y 2
= 7x 2 + 48xy – 7y 2

(iii) (a 2 + b) (a + b 2 )
= a 2 (a + b 2 ) + b(a + b 2 )
= (a 2 × a) + (a 2 × b 2 ) + (b × a) + (b × b 2 )
= a 3 + a 2 b 2 + ab + b 3

(iv) (p 2 – q 2 )(2p + q)
= p 2 (2p + q) – q 2 (2p + q)
= (p 2 × 2p) + (p 2 × q) – (q 2 × 2p) – (q 2 × q)
= 2p 3 + p 2 q – 2pq 2 – q 3

प्रश्न 3.
सरल कीजिए:
(i) (x 2 – 5) (x + 5) + 25
(ii) (a 2 + 5)(b 3 + 3) + 5
(iii) (t + s 2 ) (t 2 – s)
(iv) (a + b) (c – d) + (a – b) (c + d) + 2(ac + bd)
(v) (x + y) (2x + y) + (x + 2y) (x – y)
(vi) (x + y)(x 2 – xy + y 2 )
(vii) (1.5x – 4y)(1.5x + 4y + 3) – 4.5x + 12y
(viii) (a + b + c) (a + b – c)
हल:
(i) (x 2 – 5) (x + 5) + 25
= x 2 (x + 5) + 5(x + 5) + 25
= x 3 + 5x 2 – 5x – 25 + 25
= x 3 + 5x 2 – 5x + 0
= x 3 + 5x 2 – 5x

(ii) (a 2 + 5)(b 3 + 3) + 5
= a 2 (b 3 + 3) + 5(b 3 + 3) + 5
= a 2 b 3 + 3a 2 + 5b 3 + 15 + 5
= a 2 b 3 + 3a 2 + 5b 3 + 20

(iii) (टी + एस 2 ) (टी 2 – एस)
= टी (टी 2 – एस) + एस 2 (टी 2 – एस)
= टी 3 – सेंट + एस 2 टी 2 – एस 3
= टी 3 + एस 2 टी 2 – सेंट – एस 3

(iv) (a + b)(c – d) + (a – b) (c + d) + 2(ac + bd)
= a(c – d) + b(c – d) + a(c + d) – b(c + d) + 2ac + 2bd
= ac – ad + bc – bd + ac + ad – bc – bd + 2ac + 2bd
= ac + ac + 2ac + bc – bc – ad + ad – bd – bd + 2bd
= 4ac + 0 + 0 + 0
= 4ac

(v) (x + y) (2x + y) + (x + 2y) (x – y)
= x(2x + y) + y(2x + y) + x(x – y) + 2y(x – y)
= 2x 2 + xy + 2xy + y 2 + x 2 – xy + 2xy – 2y 2
= 2x 2 + x 2 + xy + 2xy – xy + 2xy + y 2 – 2y 2
= 3x 2 + 4xy – y 2

(vi) (x + y)(x 2 – xy + y 2 )
= x(x 2 – xy + y 2 ) + y(x 2 – xy + y 2 )
= x 3 – x 2 y + x 2 y + xy 2 – xy 2 + y 3
= x 3 – 0 + 0 + y 3
= x 3 + y 3

(vii) (1.5x – 4y)(1.5x + 4y + 3) – 4.5x.+ 12y
= 1.5x (1.5x + 4y + 3) – 4y(1.5x + 4y + 3) – 4.5x + 12y
= 2.25x 2 + 6xy + 4.5x – 6xy – 16y 2 – 12y – 4.5x + 12y
= 2.25x 2 + 6xy – 6xy + 4.5x – 4.5x + 12y – 12y – 16y 2
= 2.25x 2 + 0 + 0 + 0 – 16y 2
= 2.25x 2 – 16y 2

(viii) (a + b + c) (a + b – c)
= a(a + b – c) + b(a + b – c) + c(a + b – c)
= a 2 + ab – ac + ab + b 2 – bc + ac + bc – c 2
= a 2 + ab + ab – bc + bc – ac + ac + b 2 – c 2
= a 2 + 2ab + b 2 – c 2 + 0 + 0
= a 2 + 2ab + b 2 – c 2

Ex 9.5

प्रश्न 1.
निम्नलिखित प्रत्येक गुणनफल को प्राप्त करने के लिए उपयुक्त सर्वसमिका का प्रयोग कीजिए।
(i) (x + 3) (x + 3)
(ii) (2y + 5) (2y + 5)
(iii) (2a – 7) (2a – 7)
(iv) (3a – 12)(3a – 12)
(v) (1.1m – 0.4) (1.1m + 0.4)
(vi) (a 2 + b 2 ) (-a 2 + b 2 )
(vii) (6x – 7) (6x + 7)
(viii) (-a + c) (-a + c)
(ix) (x2+3y4)(x2+3y5)
(x) (7a – 9b) (7a – 9b)
उत्तर:
(i) (x + 3) (x + 3) = (x + 3) 2
= x 2 + 2 × x × 3 + 3 2
= x 2 + 6x +9
[पहचान (a + b) 2 = a 2 + 2ab + b 2 का उपयोग करके ]

(ii) (2y + 5) (2y + 5) = (2y + 5) 2
= (2y) 2 + 2 × 2y × 5 + 5 2
= 4y 2 + 20y + 25
[पहचान (a + b) 2 = a 2 + 2ab + b 2 का उपयोग करके ]

(iii) (2a – 7) (2a – 7) = (2a – 7) 2
= (2a) 2 – 2 × 2a × 7 + (7) 2
[पहचान (a – b) 2 = a 2 -2ab + b 2 का उपयोग करके ]
= 4a 2 – 28a + 49

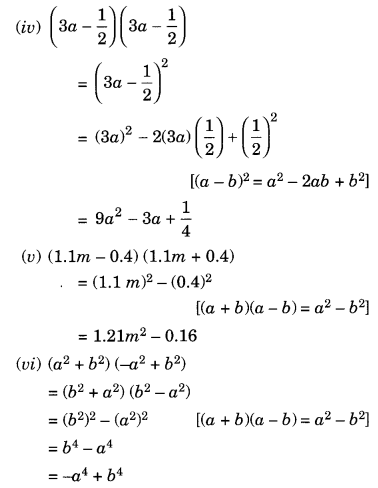
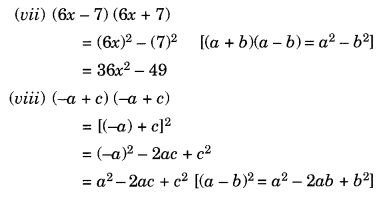
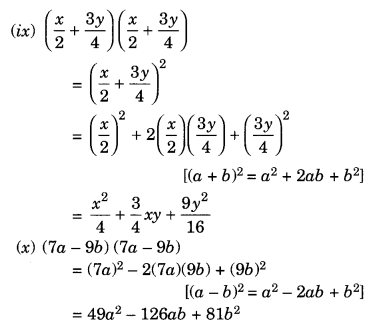
प्रश्न 2.
सर्वसमिका (x + a)(x + b) = x 2 + (a + b)x + ab का प्रयोग करके निम्नलिखित गुणनफल ज्ञात कीजिए।
(i) (x + 3) (x + 7)
(ii) (4x + 5)(4x + 1)
(iii) (4x – 5) (4x – 1)
(iv) (4x + 5) (4x – 1)
(v) (2x + 5y) (2x + 3y)
(vi) (2a 2 + 9) (2a 2 + 5)
(vii) (xyz – 4) (xyz – 2)
हल: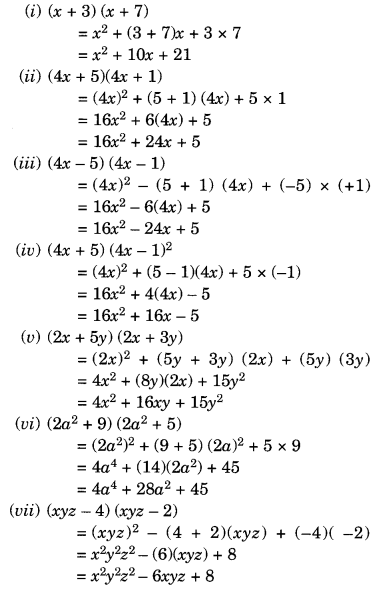

प्रश्न 3.
सरल कीजिए:
(i) (a 2 – b 2 ) 2
(ii) (2x + 5) 2 – (2x – 5) 2
(iii) (7m – 8n) 2 + (7m + 8n) 2
(iv) (4m + 5n) 2 + (5m + 4n) 2
(v) (2.5p – 1.5q) 2 – (1.5p – 2.5q) 2
(vi) (ab + bc) 2 – 2ab 2 c
(vii) (m 2 – n 2 m) 2 + 2m 3 n 2
हल: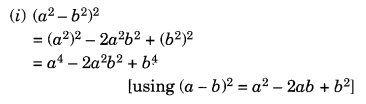

प्रश्न 4.
दर्शाइए कि:
(i) (3x + 7) 2 – 84x = (3x – 7) 2
(ii) (9p – 5q) 2 + 180pq = (9p + 5q) 2
हल:

प्रश्न 5.
सर्वसमिकाओं का प्रयोग करते हुए, मूल्यांकन करें:
(i) 71 2
(ii) 99 2
(iii) 102 2
(iv) 998 2
(v) 5.2 2
(vi) 297 × 303
(vii) 78 × 82
(viii) 8.9 2
(ix) 1.05 × 9.5
हल:

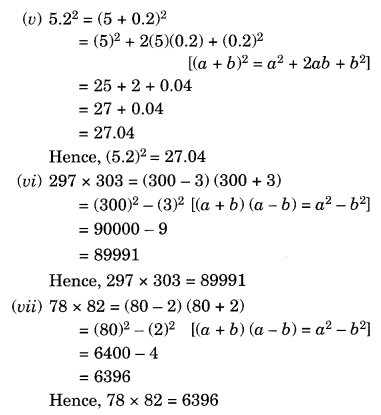
प्रश्न 6.
a 2 – b 2 = (a + b) (a – b) का उपयोग करके, ज्ञात कीजिए
(i) 51 2 – 49 2
(ii) (1.02) 2 – (0.98) 2
(iii) 153 2 – 147 2
(iv) 12.1 2 – 7.9 2
हल:
(i) 51 2 – 49 2 = (51 + 49) (51 – 49) = 100 × 2 = 200
(ii) (1.02) 2 – (0.98) 2 = (1.02 + 0.98) (1.02 – 0.98) = 2.00 × 0.04 = 0.08
(iii) 153 2 – 147 2 = (153 + 147) (153 – 147) = 300 × 6 = 1800
(iv) 12.1 2 – 7.9 2 = (12.1 + 7.9) (12.1 – 7.9) = 20.0 × 4.2 = 84

प्रश्न 7.
(x + a) (x + b) = x 2 + (a + b)x + ab का प्रयोग करते हुए, ज्ञात कीजिए:
(i) 103 × 104
(ii) 5.1 × 5.2
(iii) 103 × 98
(iv) 9.7 × 9.8
हल:
(i) 103 × 104 = (100 + 3)(100 + 4) = (100) 2 + (3 + 4) (100) + 3 × 4 = 10000 + 700 + 12 = 10712
(ii) 5.1 × 5.2 = (5 + 0.1) (5 + 0.2) = (5) 2 + (0.1 + 0.2) (5) + 0.1 × 0.2 = 25 + 1.5 + 0.02 = 26.5 + 0.02 = 26.52
(iii) 103 × 98 = (100 + 3) (100 – 2) = (100) 2 + (3 – 2) (100) + 3 × (-2) = 10000 + 100 – 6 = 10100 – 6 = 10094
(iv) 9.7 × 9.8 = (10 - 0.3) (10 - 0.2) = (10) 2 - (0.3 + 0.2) (10) + (-0.3) (-0.2) = 100 - 5 + 0.06 = 95 + 0.06 = 95.06