NCERT Class 8 Maths Chapter 3 चतुर्भुजों को समझना
NCERT Solutions for Class 8 Maths Chapter 3 चतुर्भुजों को समझना
Ex 3.1
प्रश्न 1.
यहाँ कुछ आकृतियाँ दी गई हैं।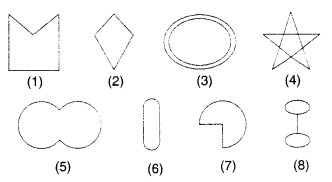
निम्नलिखित के आधार पर उनमें से प्रत्येक को वर्गीकृत करें।
(a) सरल वक्र
(b) सरल बंद वक्र
(c) बहुभुज
(d) उत्तल बहुभुज
(e) अवतल बहुभुज
हल:
(a) सरल वक्र हैं: (1), (2), (5) (6) और (7)
(b) सरल बंद वक्र हैं: (1), (2), (5), (6) और (7) और (4)
(c) बहुभुज हैं: (1) और (2)
(d) उत्तल बहुभुज है: (2)
(e) अवतल बहुभुज है: (1) और (4)
प्रश्न 2.
निम्नलिखित में से प्रत्येक के कितने विकर्ण हैं?
(a) एक उत्तल चतुर्भुज
(b) एक सम षट्भुज
(c) एक त्रिभुज।
हल:
(a) → 2
(b) → 9
(c) → 0
प्रश्न 3.
एक उत्तल चतुर्भुज के कोणों के मापों का योग क्या होता है? यदि चतुर्भुज उत्तल न हो, तो क्या यह गुण लागू होगा? (एक अउत्तल चतुर्भुज बनाकर देखिए!)
हल:
एक उत्तल चतुर्भुज के कोणों के मापों का योग 360° होता है।
हाँ, यह गुण लागू होता है, भले ही चतुर्भुज उत्तल न हो।
प्रश्न 4.
तालिका का परीक्षण करें।
प्रत्येक (आकृति त्रिभुजों में विभाजित है और उससे निकाले गए कोणों का योग)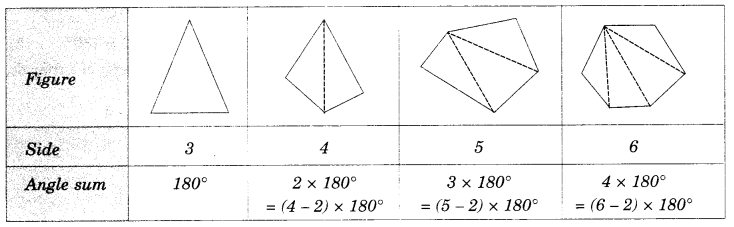
भुजाओं की संख्या वाले उत्तल बहुभुज के कोणों के योग के बारे में आप क्या कह सकते हैं?
(a) 7
(b) 8
(c) 10
(d) n
हल:
(a) जब n = 7
बहुभुज के आंतरिक कोणों का योग = (7 – 2) × 180°
= 5 × 180°
= 900°
(b) जब n = 8
बहुभुज के आंतरिक कोणों का योग = (8 – 2) × 180°
= 6 × 180°
= 1080°
(c) जब n = 10 10
भुजाओं वाले बहुभुज के आंतरिक कोणों का योग = (10 – 2) × 180°
= 8 × 180°
= 1440°
(d) जब n = n
बहुभुज के आंतरिक कोणों का योग = (n – 2) × 180°
प्रश्न 5.
एक नियमित बहुभुज क्या है?
(i) 3 स्लाइड
(ii) 4 स्लाइड
(iii) 6 स्लाइड
वाले नियमित बहुभुज का नाम बताइए ।
हल:
एक बहुभुज, जो 'समबाहु' और 'समानकोणिक' दोनों है, एक नियमित बहुभुज कहलाता है।
(i) 3 स्लाइड
3 स्लाइड वाले नियमित बहुभुज का नाम एक समबाहु त्रिभुज है।
(ii) 4 स्लाइड
4 स्लाइड वाले नियमित बहुभुज का नाम वर्ग है।
(iii) 6 स्लाइड
6 स्लाइड वाले नियमित बहुभुज का नाम एक नियमित षट्भुज है।
प्रश्न 6.
निम्नलिखित आकृतियों में कोण का माप x ज्ञात कीजिए।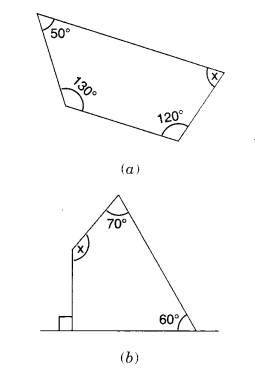
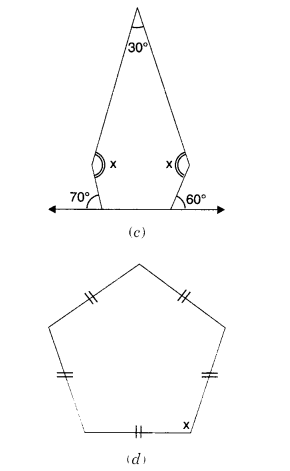
हल:
(a) एक चतुर्भुज के आंतरिक कोणों का योग 360° है
∴ x + 120° + 130° + 50° = 360°
⇒ x + 300° = 360°
⇒ x = 360° – 300°
⇒ x = 60°
(b) चतुर्भुज के आंतरिक कोणों का योग 360° होता है
∴ x + 70° + 60° + 90° = 360°
⇒ x + 220° = 360°
⇒ x = 360° – 220°
⇒ x = 140°
(c) आंतरिक कोण 30°, x°, (180 – 60°), (180° – 70°) और x° हैं,
अर्थात, 30°, x°, 120°, 110° और x°
दी गई आकृति एक पंचभुज है।
पंचभुज के आंतरिक कोणों का योग = 540°
∴ 30° + x ° + 120° + 110° + x = 540°
⇒ 2x° + 260° = 540°
⇒ 2x° = 540° – 260°
⇒ 2x°= 280°
⇒ x = \(\frac{280^{\circ}}{2}\)
⇒ x = 140°
x का माप 140° है।
(d) यह एक सम पंचभुज है।
सम पंचभुज के सभी आंतरिक कोणों का योग = 540°
इसका प्रत्येक कोण x° के बराबर है।
x° + x° + x° + x° + x° = 540°
⇒ 5x° = 540°
⇒ x = \(\frac{540^{\circ}}{5}\)
⇒ x = 108°
x का माप 108° है।
प्रश्न 7.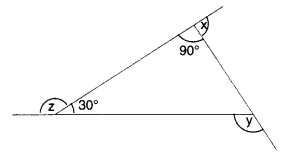
(a) x + y + z ज्ञात कीजिए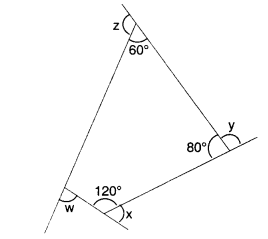
(b) x + y + z + w ज्ञात कीजिए
हल:
(a) x + 90° = 180° (रैखिक युग्म)
x = 180° – 90° = 90°
y = 30° + 90° [∵ त्रिभुज का बाह्य कोण अंतः सम्मुख कोणों के योग के बराबर होता है]
⇒ y = 120°
z + 30° = 180° (रैखिक युग्म)
⇒ z = 180° – 30° = 150°
∴ x + y + z = 90° + 120° + 150° = 360°
(b) चतुर्भुज के आंतरिक कोणों का योग = 360°
⇒ ∠1 + 120° + 80° + 60° = 360°
⇒ ∠1 + 260° = 360°
⇒ ∠1 = 360° – 260° = 100°
अब, x + 120° = 180° (रैखिक युग्म)
x = 180° – 120° = 60°
y + 80° = 180° (रैखिक युग्म)
⇒ y = 180° – 80° = 100°
z + 60° = 180° (रैखिक युग्म)
⇒ z = 180° – 60°
⇒ z = 120°
w + ∠1 = 180° (रैखिक युग्म)
⇒ w + 100°= 180°
⇒ w = 180° – 100° = 80°
इस प्रकार x + y + z + w = 60° + 100° + 120° + 80° = 360°
Ex 3.2
प्रश्न 1.
निम्नलिखित आकृतियों में x ज्ञात कीजिए।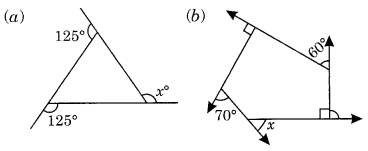
हल:
(a) हम जानते हैं कि बहुभुज के सभी बाह्य कोणों का योग = 360°
125° + 125° + x = 360°
⇒ 250° + x = 360°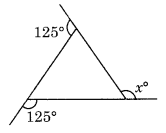
x = 360° – 250° = 110°
अतः x = 110°
(b) यहाँ ∠y = 180° – 90° = 90°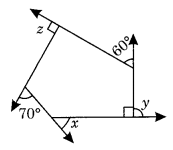
और ∠z = 90° (दिया गया है)
x + y + 60° + z + 70° = 360° [∵ बहुभुज के सभी बाह्य कोणों का योग = 360°]
⇒ x + 90° + 60° + 90° + 70° = 360°
⇒ x + 310° = 360°
⇒ x = 360° – 310° = 50°
अतः x = 50°
प्रश्न 2.
एक नियमित बहुभुज के प्रत्येक बाह्य कोण का माप ज्ञात कीजिए जिसमें
(i) 9 भुजाएँ हैं
(ii) 15 भुजाएँ हैं
हल:
(i) भुजाओं की संख्या (n) = 9
बाह्य कोणों की संख्या = 9
दिया गया बहुभुज एक नियमित बहुभुज है
सभी बाह्य कोण बराबर हैं
एक बाह्य कोण का माप = \(\frac{360^{\circ}}{9}\) = 40°
(ii) सम बहुभुज की भुजाओं की संख्या = 15
बराबर बाह्य कोणों की संख्या =15
सभी बाह्य कोणों का योग = 360°
प्रत्येक बाह्य कोण का माप = \(\frac{360^{\circ}}{15}\) = 24°
प्रश्न 3.
यदि एक समबहुभुज के बाह्य कोण का माप 24° है, तो इसमें कितनी भुजाएँ होंगी?
हल:
समबहुभुज के सभी बाह्य कोणों का योग = 360°
भुजाओं की संख्या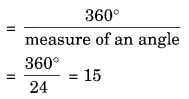
अतः, भुजाओं की संख्या = 15
प्रश्न 4.
एक समबहुभुज में कितनी भुजाएँ होंगी यदि उसका प्रत्येक अंतः कोण 165° का हो?
हल:
मान लीजिए कि समबहुभुज की भुजाओं की संख्या r है।
सभी अंतः कोणों का योग = (n – 2) × 180°
और, इसके प्रत्येक कोण का माप =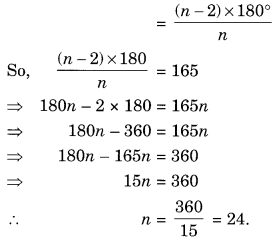
24 है। अतः, भुजाओं की संख्या = 24
प्रश्न 5.
(a) क्या प्रत्येक बाह्य कोण a का माप 22° के साथ एक नियमित बहुभुज होना संभव है?
(b) क्या यह एक नियमित बहुभुज का आंतरिक कोण हो सकता है? क्यों?
हल:
(a) चूंकि, एक नियमित बहुभुज के सभी बाहरी कोणों का योग = 360° है जो 22° से विभाज्य नहीं है।
यह संभव नहीं है कि एक नियमित बहुभुज का बाहरी कोण 22° हो। (b) भुजा n = (n - 2) × 180° वाले एक नियमित बहुभुज के सभी आंतरिक कोणों का योग एक पूर्ण संख्या नहीं है। चूंकि भुजाओं की संख्या भिन्नों में नहीं हो सकती है। एक नियमित बहुभुज के लिए इसका आंतरिक कोण = 22° होना संभव नहीं है।

प्रश्न 6.
(a) एक नियमित बहुभुज के लिए न्यूनतम संभव आंतरिक कोण क्या है? क्यों?
(b) एक नियमित बहुभुज के लिए अधिकतम संभव बाहरी कोण क्या है?
हल:
(a) भुजा n = (n – 2) × 180° वाले एक नियमित बहुभुज के सभी आंतरिक कोणों का योग
प्रत्येक आंतरिक कोण का माप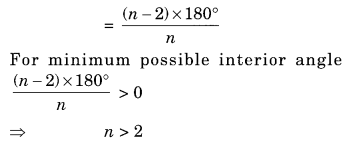
एक समबाहु त्रिभुज (n = 3) के कोण का न्यूनतम माप = 60° है।
(b) भाग (a) से हम यह निष्कर्ष निकाल सकते हैं कि एक नियमित बहुभुज का अधिकतम बाहरी कोण = 180° – 60° = 120° है।
Ex 3.3
प्रश्न 1.
एक समांतर चतुर्भुज ABCD दिया गया है। प्रत्येक कथन को परिभाषा या प्रयुक्त गुण के साथ पूरा करें।
(i) AD = …………
(ii) ∠DCB = ………
(iii) OC = ………
(iv) m∠DAB + m∠CDA = ……..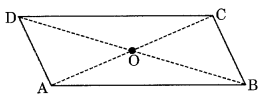
हल:
(i) AD = BC [समांतर चतुर्भुज की सम्मुख भुजाएँ बराबर होती हैं]
(ii) ∠DCB = ∠DAB [समांतर चतुर्भुज के सम्मुख कोण बराबर होते हैं]
(iii) OC = OA [समांतर चतुर्भुज के विकर्ण एक दूसरे को समद्विभाजित करते हैं]
(iv) m∠DAB + m∠CDA = 180° [समांतर चतुर्भुज के आसन्न कोण संपूरक होते हैं]
प्रश्न 2.
निम्नलिखित समांतर चतुर्भुजों पर विचार करें। अज्ञात x, y, z के मान ज्ञात कीजिए।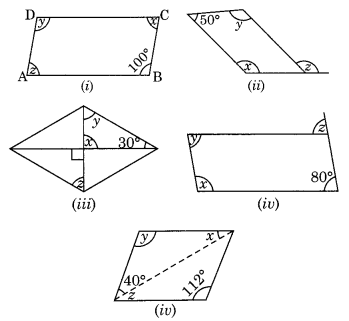
हल:
(i) ABCD एक समांतर चतुर्भुज है।
∠B = ∠D [समांतर चतुर्भुज के सम्मुख कोण बराबर होते हैं]
∠D = 100°
⇒ y = 100°
∠A + ∠B = 180° [समांतर चतुर्भुज के आसन्न कोण संपूरक होते हैं]
⇒ z + 100° = 180°
⇒ z = 180° – 100° = 80°
∠A = ∠C [a ||gm के सम्मुख कोण]
x = 80°
अतः x = 80°, y = 100° और z = 80°
(ii) PQRS एक समांतर चतुर्भुज है।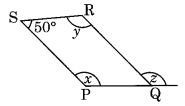
∠P + ∠S = 180° [समांतर चतुर्भुज के आसन्न कोण]
⇒ x + 50° = 180°
x = 180° – 50° = 130°
अब, ∠P = ∠R [विपरीत कोण बराबर हैं]
⇒ x = y
⇒ y = 130°
साथ ही, y = z [एकांतर कोण]
z = 130°
इसलिए, x = 130°, y = 130° और z = 130°
(iii) ABCD एक समचतुर्भुज है।
[∵ विकर्ण 90° पर प्रतिच्छेद करते हैं]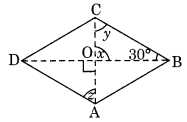
x = 90°
अब ∆OCB में,
x + y + 30° = 180° (कोण योग गुण)
⇒ 90° + y + 30° = 180°
⇒ y + 120° = 180°
⇒ y = 180° – 120° = 60°
y = z (एकांतर कोण)
⇒ z = 60°
अतः, x = 90°, y = 60° और z = 60°।
(iv) ABCD एक समांतर चतुर्भुज है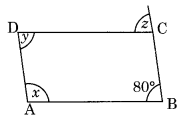
∠A + ∠B = 180° (समांतर चतुर्भुज के आसन्न कोण संपूरक होते हैं)
⇒ x + 80° = 180°
⇒ x = 180° – 80° = 100°
अब, ∠D = ∠B [a |jgm के विपरीत कोण]
⇒ y = 80°
साथ ही, z = ∠B = 80° (एकांतर कोण)
इसलिए x = 100°, y = 80° और z = 80°
(v) ABCD एक समांतर चतुर्भुज है।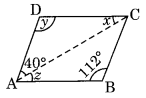
∠D = ∠B [a ||gm के विपरीत कोण]
y = 112°
x + y + 40° = 180° [कोण योग गुण]
⇒ x + 112° + 40° = 180°
⇒ x + 152° = 180°
⇒ x = 180° – 152 = 28°
z = x = 28° (वैकल्पिक कोण)
अतः x = 28°, y = 112°, z = 28°.
प्रश्न 3.
क्या चतुर्भुज ABCD एक समांतर चतुर्भुज हो सकता है यदि
(i) ∠D + ∠B = 180°?
(ii) AB = DC = 8 सेमी, AD = 4 सेमी और BC = 4.4 सेमी?
(iii) ∠A = 70° और ∠C = 65°?
हल:
(i) ∠D + ∠B = 180 के लिए, चतुर्भुज ABCD एक समांतर चतुर्भुज हो सकता है यदि निम्नलिखित शर्तें भी पूरी होती हैं।
(a) आसन्न कोणों के मापों का योग 180° होना चाहिए।
(b) विपरीत कोणों के माप भी समान होने चाहिए। इसलिए, ABCD हो सकता है लेकिन एक समांतर चतुर्भुज होना आवश्यक नहीं है।
(ii) दिया गया है: AB = DC = 8 सेमी, AD = 4 सेमी, BC = 4.4 सेमी
एक समांतर चतुर्भुज में, विपरीत भुजाएँ बराबर होती हैं।
यहाँ AD ≠ BC
इस प्रकार, ABCD एक समांतर चतुर्भुज नहीं हो सकता।
(iii) ∠A = 70° और ∠C = 65°
चूँकि ∠A ≠ ∠C
चतुर्भुज के सम्मुख कोण बराबर नहीं होते हैं।
अतः ABCD एक समांतर चतुर्भुज नहीं है।
प्रश्न 4.
एक चतुर्भुज की कच्ची आकृति बनाइए जो समांतर चतुर्भुज नहीं है, लेकिन उसके ठीक दो विपरीत कोण बराबर माप के हैं।
हल:
ABCD एक चतुर्भुज की कच्ची आकृति है जिसमें m∠A = m∠C है, लेकिन यह समांतर चतुर्भुज नहीं है। यह एक पतंग है।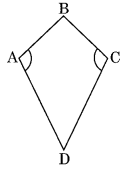
प्रश्न 5.
एक समान्तर चतुर्भुज के दो आसन्न कोणों का माप 3 : 2 के अनुपात में है। समान्तर चतुर्भुज के प्रत्येक कोण का माप ज्ञात कीजिए।
हल:
मान लीजिए ABCD एक समांतर चतुर्भुज है जिससे
m∠B : m∠C = 3 : 2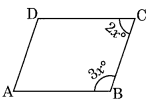
मान लीजिए m∠B = 3x° और m∠C = 2x°
m∠B + m∠C = 180° (आसन्न कोणों का योग = 180°)
3x + 2x = 180°
⇒ 5x = 180°
⇒ x = 36°
इस प्रकार, ∠B = 3 × 36 = 108°
∠C = 2 × 36° = 72°
∠B = ∠D = 108°
और ∠A = ∠C = 72°
इसलिए, समांतर चतुर्भुज के कोणों के माप 108°, 72°, 108° और 72° हैं।
प्रश्न 6.
एक समांतर चतुर्भुज के दो आसन्न कोणों का माप बराबर है। समांतर चतुर्भुज के प्रत्येक कोण का माप ज्ञात कीजिए।
हल:
मान लीजिए ABCD एक समांतर चतुर्भुज है जिसमें
∠A = ∠B
हम जानते हैं कि ∠A + ∠B = 180° [आसन्न कोणों का योग = 180°]
∠A + ∠A = 180°
⇒ 2∠A = 180°
⇒ ∠A = 90°
इस प्रकार, ∠A = ∠C = 90° और ∠B = ∠D = 90°
[एक समांतर चतुर्भुज के सम्मुख कोण बराबर होते हैं]
प्रश्न 7.
आसन्न आकृति HOPE एक समांतर चतुर्भुज है। कोण x, y और z के माप ज्ञात कीजिए। इन्हें ज्ञात करने के लिए आप किन गुणों का उपयोग करते हैं?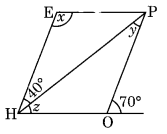
हल:
∠y = 40° (एकांतर कोण)
∠z + 40° = 70° (बाह्य कोण गुण)
⇒ ∠z = 70° – 40° = 30°
z = ∠EPH (एकांतर कोण)
∆EPH में
∠x + 40° + ∠z = 180° (आसन्न कोण)
⇒ ∠x + 40° + 30° = 180°
⇒ ∠x + 70° = 180°
⇒ ∠x = 180° – 70° = 110°
इसलिए x = 110°, y = 40° और z = 30°।
प्रश्न 8.
निम्नलिखित आकृतियाँ GUNS और RUNS समांतर चतुर्भुज हैं। x और y ज्ञात कीजिए। (लंबाई सेमी में है)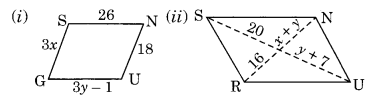
हल:
(i) GU = SN (समांतर चतुर्भुज की सम्मुख भुजाएँ)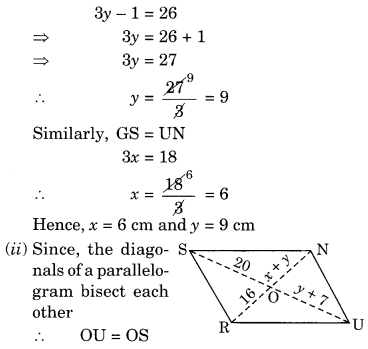
⇒ y + 7 = 20
⇒ y = 20 – 7 = 13
साथ ही, ON = OR
⇒ x + y = 16
⇒ x + 13 = 16
x = 16 – 13 = 3
अतः, x = 3 सेमी और y = 13 सेमी।
प्रश्न 9.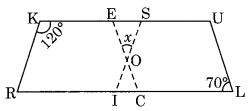
उपरोक्त आकृति में RISK और CLUE दोनों समांतर चतुर्भुज हैं। x का मान ज्ञात कीजिए।
हल:
यहाँ RISK और CLUE दो समांतर चतुर्भुज हैं।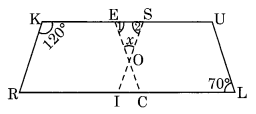
∠1 = ∠L = 70° (समानांतर चतुर्भुज के विपरीत कोण)
∠K + ∠2 = 180°
आसन्न कोणों का योग 180° है
120° + ∠2 = 180°
∠2 = 180° – 120° = 60°
∆OES में,
∠x + ∠1 + ∠2 = 180° (कोण योग गुण)
⇒ ∠x + 70° + 60° = 180°
⇒ ∠x + 130° = 180°
⇒ ∠x = 180° – 130° = 50°
इसलिए x = 50°
प्रश्न 10.
समझाइए कि यह आकृति एक समलम्ब चतुर्भुज कैसे है। इसकी कौन सी दो भुजाएँ समांतर हैं?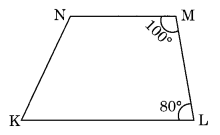
हल:
∠M + ∠L = 100° + 80° = 180°
∠M और ∠L आसन्न कोण हैं, और आसन्न अंतः कोणों का योग 180° है।
KL, NM के समांतर है।
अतः KLMN एक समलम्ब चतुर्भुज है।
प्रश्न 11.
नीचे दी गई आकृति में m∠C ज्ञात कीजिए यदि AB || DC है।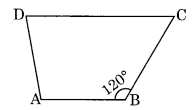
हल:
AB || DC और BC एक तिर्यक रेखा है,
∵ m∠B + m∠C = 180°
अंतः कोणों का योग 180° है
m∠C = 180° – m∠B
∴ m∠C = 180° – 120° = 60°
प्रश्न 12.
आकृति में यदि SP || QR है तो ∠P और ∠S का माप ज्ञात कीजिए। (यदि आप m∠R ज्ञात करते हैं, तो क्या m∠P ज्ञात करने की एक से अधिक विधियाँ हैं?)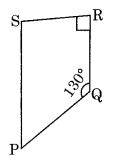
हल:
PQRS एक समलम्ब चतुर्भुज है जिससे SP || RQ और PQ एक तिर्यक रेखा है।
∴ m∠P + m∠Q = 180° (आंतरिक कोण संपूरक हैं)
m∠P + 130° = 180°
m∠P = 180° – 130° = 50°
इसके अलावा, m∠S + m∠R = 180°
⇒ m∠S + 90° = 180°
⇒ m∠S = 180° – 90°
⇒ m∠S = 90°
m∠P + m∠Q + m∠R + m∠S = 360° (चतुर्भुज के कोणों का योग 360° होता है)
⇒ m∠P + 130° + 90° + 90° = 360°
⇒ m∠P + 130° + 90° + 90° = 360°
⇒ m∠P + 130° + 90° + 90° = 360°
⇒ m∠P + 310° = 360°
⇒ m∠P = 360° – 310°
⇒ m∠P = 50°
अतः, m∠P = 50° और m∠S = 90°
Ex 3.4
प्रश्न 1.
बताइए कि कौन सा कथन सत्य है या असत्य।
(a) सभी आयत वर्ग होते हैं।
(b) सभी समचतुर्भुज समांतर चतुर्भुज होते हैं।
(c) सभी वर्ग समचतुर्भुज और आयत भी होते हैं।
(d) सभी वर्ग समांतर चतुर्भुज नहीं होते हैं।
(e) सभी पतंग समचतुर्भुज होते हैं।
(f) सभी समचतुर्भुज पतंग होते हैं।
(g) सभी समांतर चतुर्भुज समलम्ब होते हैं।
(h) सभी वर्ग समलम्ब होते हैं।
हल:
(a) असत्य
(b) सत्य
(c) सत्य
(d) असत्य
(e) असत्य
(f) सत्य
(g) सत्य
(h) सत्य
प्रश्न 2.
उन सभी चतुर्भुजों की पहचान करें जिनमें
(a) समान लंबाई की चार भुजाएँ हों
(b) चार समकोण हों।
हल:
(a) वर्ग और समचतुर्भुज।
(b) आयत और वर्ग।
प्रश्न 3.
व्याख्या कीजिए कि वर्ग कैसे होता है:
(i) एक चतुर्भुज
(ii) एक समांतर चतुर्भुज
(iii) एक समचतुर्भुज
(iv) एक आयत
हल:
(i) वर्ग एक चतुर्भुज है क्योंकि यह चार रेखाखंडों से बंद होता है।
(ii) वर्ग निम्नलिखित गुणों के कारण एक समांतर चतुर्भुज है:
(a) सम्मुख भुजाएँ बराबर और समांतर होती हैं।
(b) सम्मुख कोण बराबर होते हैं।
(iii) वर्ग एक समचतुर्भुज है क्योंकि इसकी सभी भुजाएँ बराबर और सम्मुख भुजाएँ समांतर होती हैं।
(iv) वर्ग एक आयत है क्योंकि इसकी सम्मुख भुजाएँ बराबर और विकर्ण बराबर होते हैं।
प्रश्न 4.
उन चतुर्भुजों के नाम बताइए जिनके विकर्ण
(i) एक दूसरे को समद्विभाजित करते हैं
(ii) एक दूसरे के लंबवत समद्विभाजक हैं
(iii) बराबर हैं
हल:
(i) समांतर चतुर्भुज, आयत, वर्ग और समचतुर्भुज
(ii) वर्ग और समचतुर्भुज
(iii) आयत और वर्ग
प्रश्न 5.
व्याख्या कीजिए कि आयत एक उत्तल चतुर्भुज क्यों होता है।
हल:
एक आयत में, उसके दोनों विकर्ण उसके अभ्यंतर में स्थित होते हैं। अतः, यह एक उत्तल चतुर्भुज होता है।
प्रश्न 6.
ABC एक समकोण त्रिभुज है और O समकोण के सम्मुख भुजा का मध्यबिंदु है। समझाइए कि O, A, B और C से समान दूरी पर क्यों है। (आपकी सहायता के लिए बिंदीदार रेखाएँ अतिरिक्त रूप से खींची गई हैं)।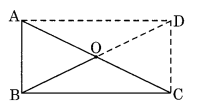
हल:
चूँकि समकोण त्रिभुज ABC, बिंदीदार रेखाओं द्वारा एक आयत ABCD बनाता है।
अतः OA = OB = OC = OD [एक आयत के विकर्ण बराबर होते हैं और एक दूसरे को समद्विभाजित करते हैं]
अतः, O, A, B और C से समान दूरी पर है।
