SikhLo - Current Affairs in Hindi, Daily current affairs, Current affairs

 NCERT Class 8 Maths Chapter 4 प्रायोगिक ज्यामिति

NCERT Solutions for Class 8 Maths Chapter 4 प्रायोगिक ज्यामिति

Ex 4.1

प्रश्न 1.
निम्नलिखित चतुर्भुजों की रचना कीजिए।
(i) चतुर्भुज ABCD
AB = 4.5 सेमी
BC = 5.5 सेमी
CD = 4 सेमी
AD = 6 सेमी
AC = 7 सेमी

(ii) चतुर्भुज JUMP
JU = 3.5 सेमी
UM = 4 सेमी
MP = 5 सेमी
PJ = 4.5 सेमी
PU = 6.5 सेमी

(iii) समांतर चतुर्भुज MORE
OR = 6 सेमी
RE = 4.5 सेमी
EO = 7.5 सेमी

(iv) समचतुर्भुज BEST
BE = 4.5 cm
ET = 6 cm
हल:
(i)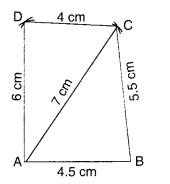

रचना के चरण:
I. एक रेखाखंड AB = 4.5 cm खींचिए।
II. A को केंद्र मानकर और त्रिज्या = 7 cm लेकर एक चाप लगाइए।
III. B को केंद्र मानकर और त्रिज्या = 5.5 cm लेकर, एक और चाप लगाइए जो पहले वाले चाप को C पर काटे।
IV. A को केंद्र मानकर और त्रिज्या = 6 cm लेकर B के विपरीत भुजा पर एक चाप लगाइए।
V. C को केंद्र मानकर और त्रिज्या = 4 cm लेकर, एक और चाप लगाइए जो पहले वाले चाप को D पर काटे।
VI. AC, BC, DA और DC को मिलाइए। इस प्रकार, ABCD अभीष्ट चतुर्भुज है।

(ii)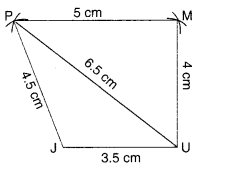

रचना के चरण:
I. एक रेखाखंड JU = 3.5 सेमी खींचिए।
II. केंद्र U और त्रिज्या UP = 6.5 सेमी लेकर एक चाप लगाइए।
III. केंद्र J और त्रिज्या = 4.5 सेमी लेकर एक और चाप लगाइए जो पहले चाप को P पर काटे।
IV. केंद्र U और त्रिज्या = 4 सेमी लेकर J के विपरीत भुजा पर एक चाप लगाइए।
V. केंद्र P और त्रिज्या = 4 सेमी लेकर एक और चाप लगाइए जो पहले चाप को M पर काटे।
VI. PJ, PU, ​​PM और UM को मिलाइए। इस प्रकार, JUMP अभीष्ट चतुर्भुज है।

(iii)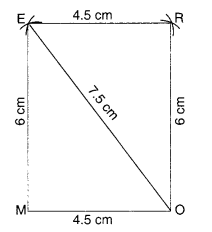

नोट: एक समांतर चतुर्भुज में विपरीत भुजाएँ बराबर होती हैं।
रचना के चरण:
I. एक रेखाखंड MO = 4.5 सेमी खींचिए।
II. केंद्र O और त्रिज्या = 7.5 सेमी लेकर एक चाप लगाइए।
III. केंद्र M और त्रिज्या = 6 सेमी लेकर एक और चाप लगाइए जो पिछले चाप को E पर काटता है।
IV. केंद्र O और त्रिज्या = 6 सेमी लेकर E के विपरीत भुजा पर एक चाप लगाइए।
V. केंद्र E और त्रिज्या = 4.5 सेमी लेकर एक और चाप लगाइए जो पिछले चाप को R पर काटता है।
VI. OR, RE, EO और EM को मिलाइए। इस प्रकार, MORE अभीष्ट समांतर चतुर्भुज है।

(iv)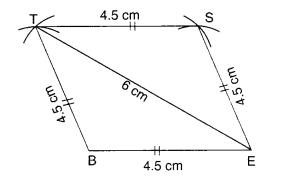

निर्माण के चरण:
I. एक रेखाखंड BE = 4.5 सेमी खींचें।
II. E को केंद्र और त्रिज्या = 6 सेमी लेकर, एक चाप बनाएं।
III. B को केंद्र और त्रिज्या = 4.5 सेमी लेकर, पहले चाप को T पर काटने के लिए एक और चाप लगाएं।
नोट: एक समचतुर्भुज की सभी 4 भुजाएँ बराबर होती हैं।
IV. TB और TE को मिलाएं।
V. T को केंद्र और त्रिज्या = 4.5 सेमी लेकर, B के विपरीत भुजा पर एक चाप बनाएं।
VI. E को केंद्र और त्रिज्या = 4.5 सेमी लेकर, पहले चाप को S पर काटने के लिए एक और चाप लगाएं।
VII. ST और SE को मिलाएं। इस प्रकार, BEST अभीष्ट समचतुर्भुज है।

Ex 4.2

प्रश्न 1.
निम्नलिखित चतुर्भुजों की रचना कीजिए।
(i) चतुर्भुज LIFT
LI = 4 सेमी
IF = 3 सेमी
TL = 2.5 सेमी
LF = 4.5 सेमी
IT = 4 सेमी

(ii) चतुर्भुज GOLD
OL = 7.5 सेमी
GL = 6 सेमी
GD = 6 सेमी
LD = 5 सेमी
OD = 10 सेमी

(iii) समचतुर्भुज BEND
BN = 5.6 सेमी
DE = 6.5 सेमी
हल:
(i)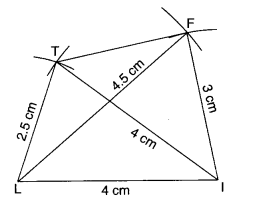

रचना के चरण:
I. एक रेखाखंड LI = 4 सेमी खींचिए।
II. I को केंद्र और त्रिज्या = 4 सेमी लेकर एक चाप खींचिए।
III. L को केंद्र और त्रिज्या = 2.5 सेमी लेकर, पहले चाप को T पर काटने के लिए एक और चाप खींचिए।
IV. TI और TL को मिलाइए।
V. L को केंद्र और त्रिज्या = 4.5 सेमी लेकर, L के विपरीत भुजा पर एक चाप खींचिए।
VI. I को केंद्र और त्रिज्या = 3 सेमी लेकर, पहले चाप को F पर काटने के लिए एक और चाप खींचिए।
VII. FL और FI को मिलाइए।
इस प्रकार, LIFT अभीष्ट चतुर्भुज है।

(ii)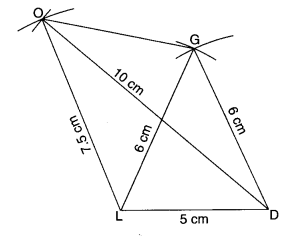

रचना के चरणः
I. LD = 5 सेमी. का एक रेखाखण्ड खींचिए।
II. L को केन्द्र मानकर तथा त्रिज्या = 6 सेमी. लेकर एक चाप लगाइए।
III. D को केन्द्र मानकर तथा त्रिज्या = 6 सेमी. लेकर एक और चाप लगाइए जो पहले चाप को G पर काटे।
IV. GL और GD को मिलाइए।
V. D को केन्द्र मानकर तथा त्रिज्या = 10 सेमी. लेकर एक चाप लगाइए।
VI. L को केन्द्र मानकर तथा त्रिज्या = 7.5 सेमी. लेकर एक और चाप लगाइए जो पहले चाप को O पर काटे।
VII. OL और OG को मिलाइए।
इस प्रकार, GOLD अभीष्ट चतुर्भुज है।

(iii)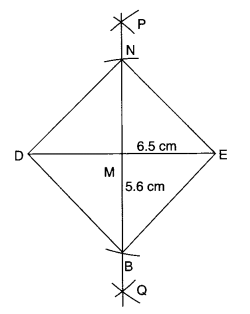

रचना के चरण:
I. 6.5 सेमी लंबा एक रेखाखंड DE खींचिए।
II. DE का लम्ब समद्विभाजक इस प्रकार खींचिए कि M, DE का मध्य-बिंदु हो।
III. M को केंद्र मानकर और 2.8 सेमी त्रिज्या लेकर, लम्ब समद्विभाजक को B और N पर प्रतिच्छेद करने वाले चाप लगाइए।
IV. ND, NE, BE और BD को मिलाइए।
इस प्रकार, BEND अभीष्ट समचतुर्भुज है।

Ex 4.3

प्रश्न 1.
निम्नलिखित चतुर्भुजों की रचना कीजिए:
(i) चतुर्भुज MORE
MO = 6 सेमी, ∠R = 105°, OR = 4.5 सेमी, ∠M = 60°, ∠O = 105°
(ii) चतुर्भुज PLAN
PL = 4 सेमी, LA = 6.5 सेमी, ∠P = 90°, ∠A = 110°, ∠N = 85°
(iii) समांतर चतुर्भुज HEAR
HE = 5 सेमी, EA = 6 सेमी, ∠R = 85°
(iv) आयत OKAY
OK = 7 सेमी, KA = 5 सेमी
हल:
(i) रचना:
चरण I: OR = 4.5 सेमी खींचिए
चरण II: चाँदे की सहायता से O और R पर 105° के दो कोण खींचिए।
चरण III: OM = 6 सेमी काटें।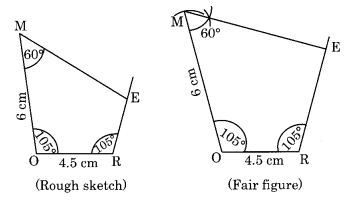

चरण IV: M पर 60° का कोण बनाएं जो R से होकर जाने वाली कोण रेखा को E पर मिले।
इस प्रकार, MORE अभीष्ट चतुर्भुज है।

(ii) रचना: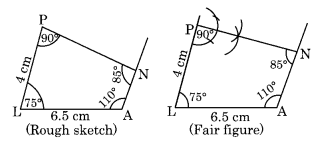

चरण I: LA = 6.5 सेमी खींचें।
चरण II: एक चांदे की सहायता से L पर 75° और A पर 110° का कोण बनाएं।
[∵ 360° – (110° + 90° + 85°) = 75°]
चरण III: LP = 4 सेमी काटें।
चरण IV: P पर 90° का कोण बनाएं जो A से होकर जाने वाली कोण रेखा को N पर मिले।
इस प्रकार PLAN अभीष्ट चतुर्भुज है।

(iii) रचना: (समान्तर चतुर्भुज की सम्मुख भुजाएँ बराबर होती हैं)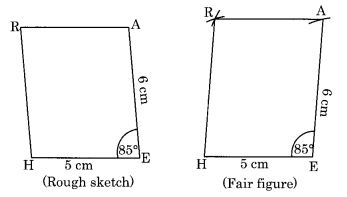

चरण I: HE = 5 सेमी खींचिए।
चरण II: E पर 85° का कोण बनाइए और EA = 6 सेमी काटिए।
चरण III: A को केंद्र मानकर 5 सेमी त्रिज्या लेकर एक चाप लगाइए।
चरण IV: H को केंद्र मानकर 6 सेमी त्रिज्या लेकर एक और चाप लगाइए जो पहले वाले चाप को R पर मिले।
चरण V: HR और AR को मिलाइए।
इस प्रकार, HEAR अभीष्ट समान्तर चतुर्भुज है।

(iv) रचना:
(एक आयत का प्रत्येक कोण 90° का होता है और सम्मुख भुजाएँ बराबर होती हैं।)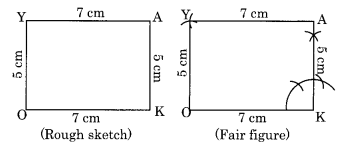

चरण I: OK = 7 सेमी बनाएँ।
चरण II: K पर 90° का कोण बनाएँ और KA = 5 सेमी काटें।
चरण III: केंद्र O और त्रिज्या 5 सेमी लेकर एक चाप बनाएँ।
चरण IV: केंद्र A और त्रिज्या 7 सेमी लेकर एक और चाप बनाएँ जो पहले वाले चाप को Y पर मिले।
चरण V: OY और AY को मिलाएँ।
इस प्रकार OKAY अभीष्ट आयत है।

Ex 4.4

प्रश्न 1.
निम्नलिखित चतुर्भुजों की रचना कीजिए:
(i) चतुर्भुज DEAR
DE = 4 सेमी, EA = 5 सेमी, AR = 4.5 सेमी, ∠E = 60°, ∠A = 90°
(ii) चतुर्भुज TRUE
TR = 3.5 सेमी, RU = 3 सेमी, UE = 4.5 सेमी, ∠R = 75°, ∠U = 120°
हल:
(i) रचना: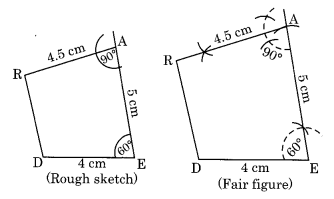

चरण I: DE = 4 सेमी खींचिए।
चरण II: E पर 60° का कोण बनाइए।
चरण III: E को केंद्र और त्रिज्या 5 सेमी लेकर एक चाप लगाइए जो कोण रेखा को A पर मिले।
चरण IV: A पर 90° का कोण बनाइए और AR = 4.5 सेमी काटिए।
चरण V: DR को मिलाइए।
इस प्रकार, DEAR अभीष्ट चतुर्भुज है।

(ii) रचना: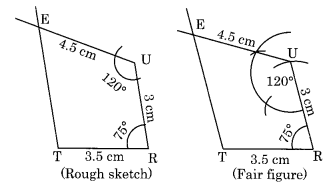

चरण I: TR = 3.5 सेमी. खींचिए।
चरण II: R पर 75° का कोण बनाइए और RU = 3 सेमी. काटिए।
चरण III: U पर 120° का कोण बनाइए और UE = 4.5 सेमी. काटिए।
चरण IV: TE को मिलाइए।
इस प्रकार, TRUE अभीष्ट चतुर्भुज है।

Ex 4.5

निम्नलिखित चित्र बनाएं।

प्रश्न 1.
RE = 5.1 सेमी वाला वर्ग READ।
हल:
रचना: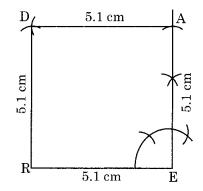

चरण I: RE = 5.1 सेमी खींचा।
चरण II: E पर 90° का कोण बनाया और EA = 5.1 सेमी काटा।
चरण III: A और R से 5.1 सेमी त्रिज्या वाले दो चाप बनाए जो एक दूसरे को D पर काटें।
चरण IV: RD और AD को मिलाया।
इस प्रकार, READ अभीष्ट वर्ग है।

प्रश्न 2.
एक समचतुर्भुज जिसके विकर्ण 5.2 सेमी और 6.4 सेमी लंबे हैं।
हल: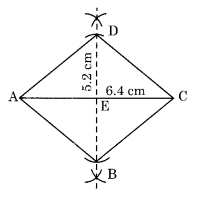

नोट: एक समचतुर्भुज के विकर्ण एक दूसरे को समकोण पर समद्विभाजित करते हैं।
रचना के चरण:
I. एक रेखाखंड AC = 5.2 सेमी खींचिए।
II. AC का लंब समद्विभाजक XY−→− खींचिए।
III. XY से, अंत OD = 12 × (6.4 सेमी) = 3.2 सेमी।
IV. इसी प्रकार, अंत OB = 12 × (6.4 सेमी) = 3.2 सेमी।
V. AD, DC, CB और BA को मिलाइए। इस प्रकार, ABCD अभीष्ट समचतुर्भुज है।

प्रश्न 3.
एक आयत जिसकी आसन्न भुजाओं की लंबाई 5 सेमी और 4 सेमी है।
हल:
रचना: माना एक आयत PQRS की दो आसन्न भुजाएँ PQ = 5 सेमी और QR = 4 सेमी हैं।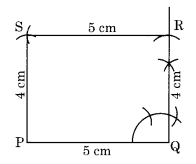

चरण I: PQ = 5 सेमी खींचें।
चरण II: Q पर 90° का कोण बनाएं और QR = 4 सेमी काटें।
चरण III: केंद्र R और त्रिज्या 5 सेमी लेकर एक चाप बनाएं।
चरण IV: केंद्र P और त्रिज्या 4 सेमी लेकर एक और चाप बनाएं जो पिछले चाप को S पर मिले।
चरण V: RS और PS को मिलाएं।
इस प्रकार, PQRS अभीष्ट आयत है।

प्रश्न 4.
एक समांतर चतुर्भुज OKAY, जहाँ OK = 5.5 सेमी और KA = 4.2 सेमी है। क्या यह अद्वितीय है?
हल:
रचना:
चरण I: OK = 5.5 सेमी खींचें।
चरण II: K पर किसी भी माप (मान लीजिए 60°) का कोण खींचें और KA = 4.2 सेमी काटें।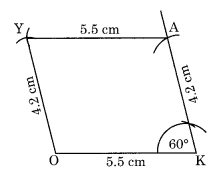

चरण III: केंद्र A और त्रिज्या 5.5 सेमी लेकर एक चाप बनाएं।
चरण IV: केंद्र O और त्रिज्या 4.2 सेमी लेकर एक और चाप बनाएं जो पिछले चाप को Y पर काटता है।
चरण V: AY और OY को मिलाएं।
इस प्रकार, OKAY अभीष्ट समांतर चतुर्भुज है।
नहीं, यह एक अद्वितीय समांतर चतुर्भुज नहीं है। K पर कोण 60° के अलावा अन्य माप का भी हो सकता है।