NCERT Class 8 Maths Chapter 6 वर्ग और वर्गमूल
NCERT Solutions for Class 8 Maths Chapter 6 वर्ग और वर्गमूल
Ex 6.1
प्रश्न 1.
निम्नलिखित संख्याओं के वर्ग का इकाई अंक क्या होगा?
(i) 81
(ii) 272
(iii) 799
(iv) 3853
(v) 1234
(vi) 20387
(vii) 52698
(viii) 99880
(ix) 12796
(x) 55555
हल:
(i) 81 का इकाई अंक 2 = 1
(ii) 272 का इकाई अंक 2 = 4
(iii) 799 का इकाई अंक 2 = 1
(iv) 3853 का इकाई अंक 2 = 9
(v) 1234 का इकाई अंक 2 = 6
(vi) 26387 का इकाई अंक 2 = 9
(vii) 52698 का इकाई अंक 2 = 4
(viii) 99880 का इकाई अंक 2 = 0
(ix) 12796 का इकाई अंक 2 = 6
(x) 55555 का इकाई अंक 2 = 5
प्रश्न 2.
निम्नलिखित संख्याएँ पूर्ण वर्ग संख्याएँ नहीं हैं। कारण बताइए।
(i) 1057
(ii) 23453
(iii) 7928
(iv) 222222
(v) 64000
(vi) 89722
(vii) 222000
(viii) 505050
हल:
(i) 1057 इकाई के स्थान पर 7 पर समाप्त होता है। इसलिए यह एक पूर्ण वर्ग संख्या नहीं है।
(ii) 23453 इकाई के स्थान पर 3 पर समाप्त होता है। इसलिए यह एक पूर्ण वर्ग संख्या नहीं है।
(iii) 7928 इकाई के स्थान पर 8 पर समाप्त होता है। इसलिए यह एक पूर्ण वर्ग संख्या नहीं है।
(iv) 222222 इकाई के स्थान पर 2 पर समाप्त होता है। इसलिए यह एक पूर्ण वर्ग संख्या नहीं है।
(v) 64000 3 शून्य पर समाप्त होता है। इसलिए यह एक पूर्ण वर्ग संख्या नहीं हो सकती।
(vi) 89722 इकाई के स्थान पर 2 पर समाप्त होता है। अतः यह एक पूर्ण वर्ग संख्या नहीं है।
(vii) 22000 3 शून्य पर समाप्त होता है। अतः यह एक पूर्ण वर्ग संख्या नहीं हो सकती।
(viii) 505050 1 शून्य पर समाप्त होता है। अतः यह एक पूर्ण वर्ग संख्या नहीं है।
प्रश्न 3.
निम्नलिखित में से किसके वर्ग विषम संख्याएँ होंगी?
(i) 431
(ii) 2826
(iii) 7779
(iv) 82004
हल:
(i) 431 2 एक विषम संख्या है।
(ii) 2826 2 एक सम संख्या है।
(iii) 7779 2 एक विषम संख्या है।
(iv) 82004 2 एक सम संख्या है।
प्रश्न 4.
निम्नलिखित पैटर्न को देखिए और लुप्त अंक ज्ञात कीजिए।
11 2 = 121
101 2 = 10201
1001 2 = 1002001
100001 2 = 1…2…1
10000001 2 = ………
हल:
उपरोक्त पैटर्न के अनुसार, हमारे पास है
100001 2 = 10000200001
10000001 2 = 100000020000001
प्रश्न 5.
निम्नलिखित पैटर्न को देखिए और लुप्त संख्याएँ भरिए।
11 2 = 121
101 2 = 10201
10101 2 = 102030201
1010101 2 = ……….
………. 2 = 10203040504030201
हल:
उपरोक्त पैटर्न के अनुसार, हमारे पास है
1010101 2 = 1020304030201
101010101 2 = 10203040504030201
प्रश्न 6.
दिए गए पैटर्न का उपयोग करके, लुप्त संख्याएँ ज्ञात कीजिए।
1 2 + 2 2 + 2 2 = 3 2
2 2 + 3 2 + 6 2 = 7 2
3 2 + 4 2 + 12 2 = 13 2
4 2 + 5 2 + …. 2 = 21 2
5 2 + …. 2 + 30 2 = 31 2
6 2 + 7 2 + ….. 2 = …… 2
हल:
दिए गए पैटर्न के अनुसार, हमारे पास है
4 2 + 5 2 + 20 2 = 21 2
5 2 + 6 2 + 30 2 = 31 2
6 2 + 7 2 + 42 2 = 43 2
प्रश्न 7.
बिना जोड़े, योगफल ज्ञात कीजिए।
(i) 1 + 3 + 5 + 7 + 9
(ii) 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19
(iii) 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 + 23
हल:
हम जानते हैं कि n विषम संख्याओं का योग = n 2
(i) 1 + 3 + 5 + 7 + 9 = (5) 2 = 25 [∵ n = 5]
(ii) 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 = (10) 2 = 100 [∵ n = 10]
(iii) 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 + 23 = (12) 2 = 144 [∵ n = 12]
प्रश्न 8.
(i) 49 को 7 विषम संख्याओं के योग के रूप में व्यक्त करें।
(ii) 121 को 11 विषम संख्याओं के योग के रूप में व्यक्त करें।
हल:
(i) 49 = 1 + 3 + 5 + 7 + 9 + 11 + 13 (n = 7)
(ii) 121 = 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 (n = 11)
प्रश्न 9.
निम्नलिखित संख्याओं के वर्गों के बीच कितनी संख्याएँ हैं?
(i) 12 और 13
(ii) 25 और 26
(iii) 99 और 100.
हल:
(i) हम जानते हैं कि n 2 और (n + 1) 2 = 2n
12 2 और 13 2 के बीच की संख्याएँ 2 = (2n) = 2 × 12 = 24
(ii) 25 2 और 26 2 = 2 × 25 = 50 (∵ n = 25)
(iii) 99 2 और 100 2 = 2 × 99 = 198 (∵ n = 99)
Ex 6.2
प्रश्न 1.
निम्नलिखित संख्याओं का वर्ग ज्ञात कीजिए।
(i) 32
(ii) 35
(iii) 86
(iv) 93
(v) 71
(vi) 46
हल:
(i) 32 = 30 + 2
(32) 2 = (30 + 2) 2
= 30(30 + 2) + 2(30 + 2)
= 30 2 + 30 × 2 + 2 × 30 + 2 2
= 900 + 60 + 60 + 4
= 1024
इस प्रकार (32) 2 = 1024
(ii) 35 = (30 + 5)
(35) 2 = (30 + 5) 2
= 30(30 + 5) + 5(30 + 5)
= (30) 2 + 30 × 5 + 5 × 30 + (5) 2
= 900 + 150 + 150 + 25
= 1225
इस प्रकार (35) 2 = 1225
(iii) 86 = (80 + 6)
86 2 = (80 + 6) 2
= 80(80 + 6) + 6(80 + 6)
= (80) 2 + 80 × 6 + 6 × 80 + (6) 2
= 6400 + 480 + 480 + 36
= 7396
इस प्रकार (86) 2 = 7396
(iv) 93 = (90+ 3)
93 2 = (90 + 3) 2
= 90 (90 + 3) + 3(90 + 3)
= (90) 2 + 90 × 3 + 3 × 90 + (3) 2
= 8100 + 270 + 270 + 9
= 8649
इस प्रकार (93) 2 = 8649
(v) 71 = (70 + 1)
71 2 = (70 + 1) 2
= 70 (70 + 1) + 1(70 + 1)
= (70) 2 + 70 × 1 + 1 × 70 + (1) 2
= 4900 + 70 + 70 + 1
= 5041
इस प्रकार (71) 2 = 5041
(vi) 46 = (40+ 6)
46 2 = (40 + 6) 2
= 40 (40 + 6) + 6(40 + 6)
= (40) 2 + 40 × 6 + 6 × 40 + (6) 2
= 1600 + 240 + 240 + 36
= 2116
इस प्रकार (46) 2 = 2116
प्रश्न 2.
एक पाइथागोरस त्रिक लिखिए जिसका एक सदस्य है
(i) 6
(ii) 14
(iii) 16
(iv) 18
हल:
(i) मान लीजिए m 2 – 1 = 6 [त्रिक 2m, m 2 – 1, m 2
+ 1 के रूप में हैं ] m 2 = 6 + 1 = 7 इसलिए, m का मान पूर्णांक नहीं होगा। अब, हम m 2 + 1 = 6 ⇒ m 2 = 6 – 1 = 5 के लिए प्रयास करते हैं। साथ ही, m का मान पूर्णांक नहीं होगा। अब हम मानते हैं 2m = 6 ⇒ m = 3 जो एक पूर्णांक है। अन्य सदस्य हैं: m 2 – 1 = 3 2 – 1 = 8 और m 2 + 1 = 3 2 + 1 = 10 इसलिए, अभीष्ट त्रिक 6, 8 और 10 हैं
(ii) मान लीजिए m 2 – 1 = 14 ⇒ m 2 = 1 + 14 = 15
m का मान पूर्णांक नहीं होगा।
अब 2m = 14 लीजिए ⇒ m = 7 जो एक पूर्णांक है।
त्रिक के सदस्य हैं 2m = 2 × 7 = 14
m 2 – 1 = (7) 2 – 1 = 49 – 1 = 48
और m 2 + 1 = (7) 2 + 1 = 49 + 1 = 50
अर्थात्, (14, 48, 50)
(iii) माना 2m = 16 m = 8
आवश्यक त्रिक हैं 2m = 2 × 8 = 16
m 2 – 1 = (8) 2 – 1 = 64 – 1 = 63
m 2 + 1 = (8) 2 + 1 = 64 + 1 = 65
यानी, (16, 63, 65)
(iv) माना 2m = 18 ⇒ m = 9
आवश्यक त्रिक हैं:
2m = 2 × 9 = 18
m 2 – 1 = (9) 2 – 1 = 81 – 1 = 80
और m 2 + 1 = (9) 2 + 1 = 81 + 1 = 82
यानी, (18, 80, 82)
Ex 6.3
प्रश्न 1.
निम्नलिखित संख्याओं में से प्रत्येक के वर्गमूल के संभावित 'इकाई' अंक क्या हो सकते हैं?
(i) 9801
(ii) 99856
(iii) 998001
(iv) 657666025
हल:
(i) संख्या 9801 के वर्गमूल का इकाई का अंक 1 या 9 हो सकता है [1 × 1 = 1, 9 × 9 = 81]
(ii) संख्या 99856 के वर्गमूल का इकाई का अंक 4 या 6 हो सकता है [4 × 4 = 16 या 6 × 6 = 36]
(iii) संख्या 998001 के वर्गमूल का इकाई का अंक 1 या 9 हो सकता है [1 × 1 = 1 या 9 × 9 = 81]
(iv) संख्या 657666025 के वर्गमूल का इकाई का अंक 5 हो सकता है [5 × 5 = 25]
प्रश्न 2.
बिना कोई गणना किए, उन संख्याओं को ज्ञात कीजिए जो निश्चित रूप से पूर्ण वर्ग नहीं हैं।
(i) 153
(ii) 257
(iii) 408
(iv) 441
हल:
हम जानते हैं कि पूर्ण वर्ग का अंतिम अंक 0, 1, 4, 5, 6 और 9 होता है।
2, 3, 7, या 8 पर समाप्त होने वाली संख्या कभी भी पूर्ण वर्ग नहीं हो सकती।
(i) 153 पूर्ण वर्ग नहीं हो सकता।
(ii) 257 पूर्ण वर्ग नहीं हो सकता।
(iii) 408 पूर्ण वर्ग नहीं हो सकता।
(iv) 441 पूर्ण वर्ग हो सकता है।
प्रश्न 3.
बार-बार घटाने की विधि द्वारा 100 और 169 के वर्गमूल ज्ञात कीजिए।
हल:
(i) √100
100 – 1 = 99
99 – 3 = 96
96 – 5 = 91
91 – 7 = 84
84 – 9 = 75
75 – 11 = 64
64 – 13 = 51
51 – 15 = 36
36 – 17 = 19
19 – 19 = 0
∴ 10 विषम संख्याओं को लगातार घटाने पर हम 0 पर पहुँचते हैं
∴ √100 = 10
(ii) √169
169 – 1 = 168
168 – 3 = 165
165 – 5 = 160
160 – 7 = 153
153 – 9 = 144
144 – 11 = 133
133 – 13 = 120
120 – 15 = 105
105 – 17 = 88
88 – 19 = 69
69 – 21 = 48
48 – 23 = 25
25 – 25 = 0
∴ 13 विषम संख्याओं को लगातार घटाने पर हम 0 पर पहुँचते हैं
∴ √169 = 13
प्रश्न 4.
अभाज्य गुणनखंड विधि द्वारा निम्नलिखित संख्याओं के वर्गमूल ज्ञात कीजिए।
(i) 729
(ii) 400
(iii) 1764
(iv) 4096 (v)
7744 (vi)
9604 (vii)
5929
(viii) 9216
(ix) 529
(x) 8100
हल:
(i) हमारे पास 729
के अभाज्य गुणनखंड हैं
729 = 3 × 3 × 3 × 3 × 3 = 3 2 × 3 2 × 3 2
√729 = 3 × 3 × 3 = 27
(ii) हमारे पास 400
के अभाज्य गुणनखंड हैं
400 = 2 × 2 × 2 × 5 × 5 = 2 2 × 2 2 × 5 2
√400 = 2 × 2 × 5 = 20
(iii) 1764
1764 = 2 × 2 × 3 × 3 × 7 × 7 = 2 2 × 3 2 × 7 2
√1764 = 2 × 3 × 7 = 42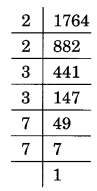
(iv) 4096
4096 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
= 2 2 × 2 2 × 2 2 × 2 2 × 2 2 √4096 = 2 × 2 × 2 × 2 × 2 × 2 = 64
(v) 7744 का अभाज्य गुणनखंडन है
7744 = 2 × 2 × 2 × 2 × 2 × 2 × 11 × 11
= 2 2 × 2 2 × 2 2 × 11 2
√7744 = 2 × 2 × 2 × 11 = 88
(vi) 9604 का अभाज्य गुणनखंडन है
9604 = 2 × 2 × 7 × 7 × 7 = 2 2 × 7 2 × 7 2
√9604 = 2 × 7 × 7 = 98
(vii) 5929 का अभाज्य गुणनखंडन है
5929 = 7 × 7 × 11 × 11 = 7 2 × 11 2
√5929 = 7 × 11 = 77
(viii) 9216 का अभाज्य गुणनखंडन है
9216 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3
= 2 2 × 2 2 × 2 2 × 2 2 × 2 2 × 3 2 √9216
= 2 × 2 × 2 × 2 × 2 × 3 = 96
(ix) 529 का अभाज्य गुणनखंडन
529 = 23 × 23 = 23 2
√529 = 23
(x) 8100 का अभाज्य गुणनखंडन
8100 = 2 × 2 × 3 × 3 × 3 × 3 × 5 × 5 = 2 2 × 3 2 × 3 2 × 5 2
√8100 = 2 × 3 × 3 × 5 = 90
प्रश्न 5.
निम्नलिखित संख्याओं में से प्रत्येक के लिए, वह सबसे छोटी पूर्ण संख्या ज्ञात कीजिए जिससे उसे गुणा किया जाए ताकि एक पूर्ण वर्ग संख्या प्राप्त हो। इस प्रकार प्राप्त वर्ग संख्या का वर्गमूल भी ज्ञात कीजिए।
(i) 252
(ii) 180
(iii) 1008
(iv) 2028
(v) 1458
(vi) 768
हल:
(i) 252 का अभाज्य गुणनखंडन
252 = 2 × 2 × 3 × 3 × 7 है
। यहाँ, अभाज्य गुणनखंडन युग्म में नहीं है। 7 का कोई युग्म नहीं है।
इस प्रकार, 7 वह सबसे छोटी पूर्ण संख्या है जिससे दी गई संख्या को गुणा करने पर एक पूर्ण वर्ग संख्या प्राप्त होती है।
नई वर्ग संख्या 252 × 7 = 1764 है।
1764 का वर्गमूल
√1764 = 2 × 3 × 7 = 42 है।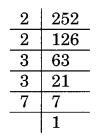
(ii) 180 का प्राइम्प गुणनखंडन
180 = 2 × 2 × 3 × 3 × 5 है।
यहाँ, 5 का कोई युग्म नहीं है।
नई वर्ग संख्या = 180 × 5 = 900।
900 का वर्गमूल
√900 = 2 × 3 × 5 = 30 है।
इस प्रकार, 5 वह सबसे छोटी पूर्ण संख्या है जिससे दी गई संख्या को गुणा करने पर वर्ग संख्या प्राप्त होती है।
(iii) 1008 का अभाज्य गुणनखंडन
1008 = 2 × 2 × 2 × 3 × 3 × 7 है।
यहाँ, 7 का कोई युग्म नहीं है।
नई वर्ग संख्या = 1008 × 7 = 7056।
अतः, 7 अभीष्ट संख्या है।
7056 का वर्गमूल
√7056 = 2 × 2 × 3 × 7 = 84 है।
(iv) 2028 का अभाज्य गुणनखंडन
2028 = 2 × 2 × 3 × 13 × 13 है
। यहाँ, 3 युग्म में नहीं है।
अतः, 3 अभीष्ट सबसे छोटी पूर्ण संख्या है।
नई वर्ग संख्या = 2028 × 3 = 6084।
6084 का वर्गमूल
√6084 = 2 × 13 × 3 = 78 है।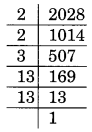
(v) 1458 का अभाज्य गुणनखंडन
1458 = 2 × 3 × 3 × 3 × 3 × 3 × 3
यहाँ, 2 युग्म में नहीं है।
अतः 2 अभीष्ट सबसे छोटी पूर्ण संख्या है।
नई वर्ग संख्या = 1458 × 2 = 2916
1458 का वर्गमूल
√2916 = 3 × 3 × 3 × 2 = 54 है।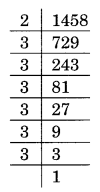
(vi) 768 का अभाज्य गुणनखंडन
768 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3 है।
यहाँ, 3 युग्म में नहीं है।
अतः, 3 अभीष्ट पूर्ण संख्या है।
नई वर्ग संख्या = 768 × 3 = 2304।
2304 का वर्गमूल
√2304 है = 2 × 2 × 2 × 2 × 3 = 48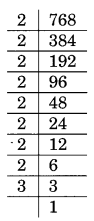
प्रश्न 6.
निम्नलिखित संख्याओं में से प्रत्येक के लिए, वह सबसे छोटी पूर्ण संख्या ज्ञात कीजिए जिससे उसे विभाजित करने पर एक पूर्ण वर्ग संख्या प्राप्त हो। इस प्रकार प्राप्त वर्ग संख्या का वर्गमूल भी ज्ञात कीजिए।
(i) 252
(ii) 2925
(iii) 396
(iv) 2645
(v) 2800
(vi) 1620
हल:
(i) 252 का अभाज्य गुणनखंडन
252 = 2 × 2 × 3 × 3 × 7 है।
यहाँ 7 का कोई युग्म नहीं है।
7 वह सबसे छोटी पूर्ण संख्या है जिससे 252 को विभाजित करने पर एक वर्ग संख्या प्राप्त होती है।
नई वर्ग संख्या = 252 ÷ 7 = 36
अतः, √36 = 6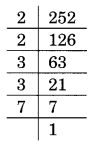
(ii) 2925 का अभाज्य गुणनखंडन:
2925 = 3 × 3 × 5 × 5 × 13
यहाँ, 13 का कोई युग्म नहीं है।
13 वह सबसे छोटी पूर्ण संख्या है जिससे 2925 को भाग देने पर एक वर्ग संख्या प्राप्त होती है।
नई वर्ग संख्या = 2925 ÷ 13 = 225
अतः √225 = 15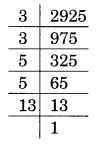
(iii) 396 का अभाज्य गुणनखंडन:
396 = 2 × 2 × 3 × 3 × 11
यहाँ 11 युग्म में नहीं है।
11 वह सबसे छोटी पूर्ण संख्या है जिससे 396 को भाग देने पर एक वर्ग संख्या प्राप्त होती है।
नई वर्ग संख्या = 396 ÷ 11 = 36
अतः √36 = 6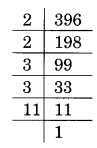
(iv) 2645 का अभाज्य गुणनखंडन
2645 = 5 × 23 × 23 है
। यहाँ, 5 युग्म में नहीं है।
5 अभीष्ट सबसे छोटी पूर्ण संख्या है।
जिससे 2645 को गुणा करने पर एक वर्ग संख्या प्राप्त होती है।
नई वर्ग संख्या = 2645 ÷ 5 = 529।
अतः, √529 = 23।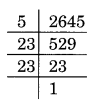
(v) 2800 का अभाज्य गुणनखंडन:
2800 = 2 × 2 × 2 × 5 × 5 × 7
यहाँ, 7 युग्म में नहीं है।
7 अभीष्ट सबसे छोटी संख्या है।
2800 को इससे गुणा करने पर एक वर्ग संख्या प्राप्त होती है।
नई वर्ग संख्या = 2800 ÷ 7 = 400
अतः √400 = 20
(vi) 1620 का अभाज्य गुणनखंडन
1620 = 2 × 2 × 3 × 3 × 3 × 3 × 5 है।
यहाँ 5 युग्म में नहीं है।
5 अभीष्ट सबसे छोटी अभाज्य संख्या है।
1620 को इससे गुणा करने पर वर्ग संख्या = 1620 ÷ 5 = 324 प्राप्त होती है।
अतः √324 = 18
प्रश्न 7.
वह सबसे छोटी वर्ग संख्या ज्ञात कीजिए जो 4, 9 और 10 में से प्रत्येक से विभाज्य हो।
हल:
4, 9, 10 का लघुत्तम समापवर्त्य = 180
4, 9 और 10 से विभाज्य सबसे छोटी संख्या = 180
अब 180 का अभाज्य गुणनखंडन है
180 = 2 × 2 × 3 × 3 × 5
यहाँ, 5 का कोई युग्म नहीं है।
अभीष्ट सबसे छोटी वर्ग संख्या = 180 × 5 = 900
प्रश्न 8.
8, 15 और 20 में से प्रत्येक से विभाज्य सबसे छोटी संख्या ज्ञात कीजिए।
हल:
8, 15 और 20 से विभाज्य सबसे छोटी संख्या उनके LCM के बराबर होती है।
LCM = 2 × 2 × 2 × 3 × 5 = 120
यहाँ, 2, 3 और 5 का कोई युग्म नहीं है।
अभीष्ट सबसे छोटी वर्ग संख्या = 120 × 2 × 3 × 5 = 120 × 30 = 3600
Ex 6.4
प्रश्न 1.
दीर्घ विभाजन विधि द्वारा निम्नलिखित संख्याओं में से प्रत्येक का वर्गमूल ज्ञात कीजिए।
(i) 2304
(ii) 4489
(iii) 3481
(iv) 529
(v) 3249
(vi) 1369
(vii) 5776
(viii) 7921
(ix) 576
(x) 1024
(xi) 3136
(xii) 900
हल: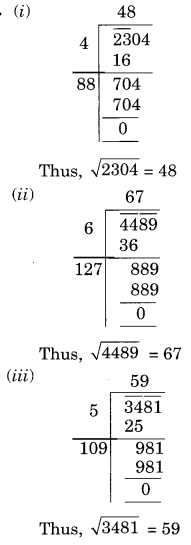
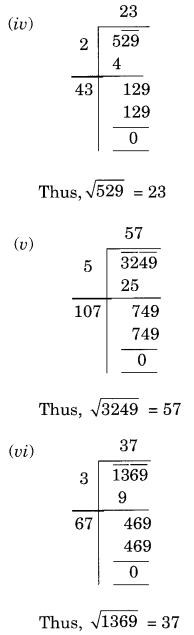
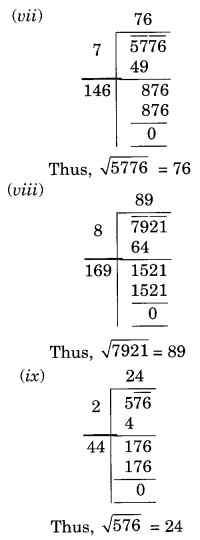
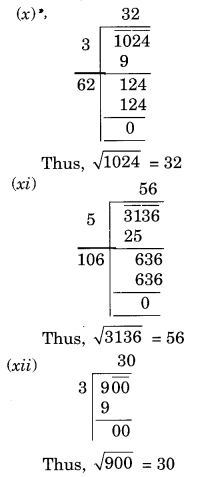
प्रश्न 2.
निम्नलिखित दशमलव संख्याओं का वर्गमूल ज्ञात कीजिए।
(i) 2.56
(ii) 7.29
(iii) 51.84
(iv) 42.25
(v) 31.36
हल: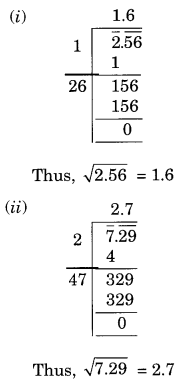
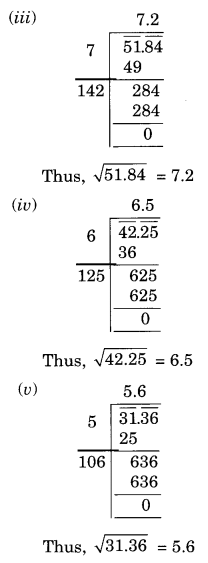
प्रश्न 3.
निम्नलिखित संख्याओं में से प्रत्येक में से वह सबसे छोटी संख्या ज्ञात कीजिए जिसे घटाने पर पूर्ण वर्ग संख्या प्राप्त हो। इस प्रकार प्राप्त पूर्ण वर्ग का वर्गमूल भी ज्ञात कीजिए।
(i) 402
(ii) 1989
(iii) 3250
(iv) 825
(v) 4000
हल:
(i)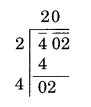
यहाँ शेषफल 2 है।
पूर्ण वर्ग संख्या प्राप्त करने के लिए 402 में से घटाने पर 2 सबसे छोटी आवश्यक संख्या है।
नई संख्या = 402 – 2 = 400
अतः, √400 = 20
(ii)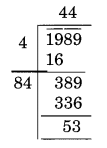
यहाँ शेषफल 53 है।
1989 में से घटाने के लिए 53 न्यूनतम आवश्यक संख्या है।
नई संख्या = 1989 – 53 = 1936
इस प्रकार, √1936 = 44
(iii)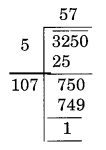
यहाँ शेषफल 1 है।
पूर्ण वर्ग संख्या प्राप्त करने के लिए 3250 में से 1 घटाने पर न्यूनतम संख्या प्राप्त होती है।
नई संख्या = 3250 - 1 = 3249।
अतः, √3249 = 57
(iv)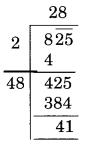
यहाँ शेषफल 41 है।
41 वह न्यूनतम संख्या है जिसे 825 में से घटाने पर पूर्ण वर्ग संख्या प्राप्त हो सकती है।
नई संख्या = 825 – 41 = 784
अतः, √784 = 28
(v)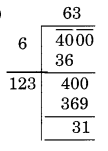
यहाँ शेषफल 31 है।
31 वह न्यूनतम संख्या है जिसे 4000 में से घटाने पर पूर्ण वर्ग संख्या प्राप्त होगी।
नई संख्या = 4000 – 31 = 3969
अतः, √3969 = 63
प्रश्न 4.
निम्नलिखित संख्याओं में से प्रत्येक में जोड़ने पर मिलने वाली सबसे छोटी संख्या ज्ञात कीजिए ताकि एक पूर्ण वर्ग संख्या प्राप्त हो। इस प्रकार प्राप्त पूर्ण वर्ग का वर्गमूल भी ज्ञात कीजिए।
(i) 525
(ii) 1750
(iii) 252
(iv) 1825
(v) 6412
हल:
(i)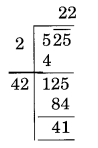
यहाँ शेषफल 41 है।
यह दर्शाता है कि 22 का वर्ग 525 से छोटा है।
अगली संख्या 23 है और 23 2 = 529
अतः, जोड़ी जाने वाली संख्या = 529 – 525 = 4
नई संख्या = 529
अतः, √529 = 23
(ii)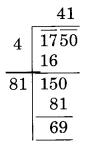
यहाँ शेषफल 69 है।
यह दर्शाता है कि 41 का वर्ग 1750 से छोटा है।
अगली संख्या 42 और 42 है। 2 = 1764
अतः, 1750 में जोड़ी जाने वाली संख्या = 1764 - 1750 = 14
आवश्यक पूर्ण वर्ग = 1764
√1764 = 42
(iii)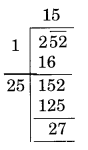
यहाँ शेषफल 27 है।
यह दर्शाता है कि 15 का वर्ग 252 से छोटा है।
अगली संख्या 16 है और 16 2 = 256
अतः, 252 में जोड़ी जाने वाली संख्या = 256 - 252 = 4
नई संख्या = 252 + 4 = 256
अभीष्ट पूर्ण वर्ग = 256
और √256 = 16
(iv)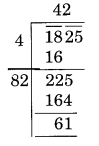
शेषफल 61 है।
यह दर्शाता है कि 42 का वर्ग 1825 से कम है।
अगली संख्या 43 है और 43 2 = 1849
अतः, 1825 में जोड़ी जाने वाली संख्या = 1849 - 1825 = 24
अभीष्ट पूर्ण वर्ग 1848 है और √1849 =43
(v)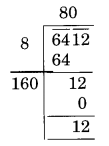
यहाँ, शेष 12 है।
यह दर्शाता है कि 80 का वर्ग 6412 से छोटा है।
अगली संख्या 81 है और 81 2 = 6561
इसलिए जोड़ी जाने वाली संख्या = 6561 - 6412 = 149
आवश्यक पूर्ण वर्ग 6561 है और √6561 = 81
प्रश्न 5.
एक वर्ग की भुजा की लंबाई ज्ञात कीजिए जिसका क्षेत्रफल = 441 m 2
हल:
माना वर्ग की भुजा की लंबाई x m है।
वर्ग का क्षेत्रफल = (भुजा) 2 = x 2 m 2
x 2 = 441 ⇒ x = √441 = 21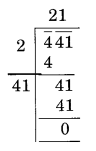
इस प्रकार, x = 21 m.
अतः वर्ग की भुजा की लंबाई = 21 m.
प्रश्न 6.
एक समकोण त्रिभुज ABC में, ∠B = 90° है।
(a) यदि AB = 6 सेमी, BC = 8 सेमी, तो AC ज्ञात कीजिए।
(b) यदि AC = 13 सेमी, BC = 5 सेमी, तो AB ज्ञात कीजिए।
हल:
(a) समकोण त्रिभुज ABC में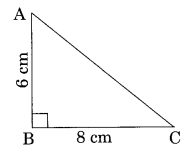
AC 2 = AB 2 + BC 2 [पाइथागोरस प्रमेय से]
⇒ AC 2 = (6) 2 + (8) 2 = 36 + 64 = 100
⇒ AC = √100 = 10
इस प्रकार, AC = 10 सेमी।
(b) समकोण त्रिभुज ABC में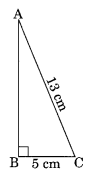
AC 2 = AB 2 + BC 2 [पाइथागोरस प्रमेय से]
⇒ (13) 2 = AB 2 + (5) 2
⇒ 169 = AB 2 + 25
⇒ 169 – 25 = AB 2
⇒ 144 = AB 2
AB = √144 = 12 सेमी
इस प्रकार, AB = 12 सेमी.
प्रश्न 7.
एक माली के पास 1000 पौधे हैं। वह इन्हें इस प्रकार लगाना चाहता है कि पंक्तियों और स्तंभों की संख्या समान रहे। इसके लिए उसे कितने पौधों की न्यूनतम संख्या और चाहिए, यह ज्ञात कीजिए।
हल:
माना पंक्तियों की संख्या x है।
और स्तंभों की संख्या भी x है।
पौधों की कुल संख्या = x × x = x 2
x 2 = 1000 ⇒ x = √1000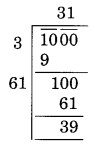
यहाँ शेषफल 39 है
इसलिए 31 का वर्ग 1000 से कम है।
अगली संख्या 32 और 32 2 = 1024 है
इसलिए जोड़ी जाने वाली संख्या = 1024 - 1000 = 24
इस प्रकार उसके लिए आवश्यक पौधों की न्यूनतम संख्या = 24।
वैकल्पिक विधि: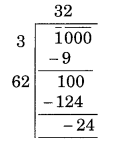
उसके लिए आवश्यक पौधों की न्यूनतम संख्या = 24।
प्रश्न 8.
एक स्कूल में 500 बच्चे हैं। पीटी ड्रिल के लिए, उन्हें इस तरह खड़ा होना है कि पंक्तियों की संख्या स्तंभों की संख्या के बराबर हो। इस व्यवस्था में कितने बच्चे बाहर रह जाएंगे?
हल:
माना एक पंक्ति में बच्चों की संख्या x है। और एक स्तंभ में भी बच्चों की संख्या x है।
छात्रों की कुल संख्या = x × x = x 2
x 2 = 500 ⇒ x = √500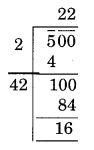
यहाँ शेष 16 है
नई संख्या 500 - 16 = 484
और, √484 = 22
इस प्रकार, इस व्यवस्था में 16 छात्र बाहर रह जाएंगे।
