SikhLo - Current Affairs in Hindi, Daily current affairs, Current affairs

 NCERT Class 8 Maths Chapter 7 घन और घनमूल

NCERT Solutions for Class 8 Maths Chapter 7 घन और घनमूल

Ex 7.1

प्रश्न 1.
निम्नलिखित में से कौन सी संख्याएँ पूर्ण घन नहीं हैं?
(i) 216
(ii) 128
(iii) 1000
(iv) 100
(v) 46656
हल:
(i) 216 का अभाज्य गुणनखंडन है:
216 = 2 × 2 × 2 × 3 × 3 × 3
उपरोक्त गुणनखंडन में, 2 और 3 ने तीन का एक समूह बनाया है।
इस प्रकार, 216 एक पूर्ण घन है।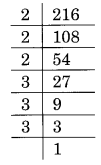

(ii) 128 का अभाज्य गुणनखंडन है:
128 = 2 × 2 × 2 × 2 × 2 × 2
यहाँ, 2 बिना तीन का समूह बनाए बचा है।
इस प्रकार 128 एक पूर्ण घन नहीं है।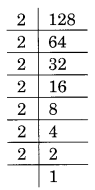

(iii) 1000 का अभाज्य गुणनखंडन है:
1000 = 2 × 2 × 2 × 5 × 5 × 5
यहाँ, तीन का समूह बनाने के लिए कोई संख्या नहीं बची है।
इस प्रकार, 1000 एक पूर्ण घन है।

(iv) 100 का अभाज्य गुणनखंडन है:
100 = 2 × 2 × 5 × 5
यहाँ 2 और 5 ने तीन का समूह नहीं बनाया है।
इस प्रकार, 100 एक पूर्ण घन नहीं है।

(v) 46656 का अभाज्य गुणनखंडन है:
46656 = 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 3 × 3 × 3
यहाँ 2 और 3 ने तीन का समूह बनाया है।
इस प्रकार, 46656 एक पूर्ण घन है।

प्रश्न 2.
निम्नलिखित संख्याओं में से प्रत्येक को किस छोटी संख्या से गुणा करने पर एक पूर्ण घन प्राप्त होगा?
(i) 243
(ii) 256
(iii) 72
(iv) 675
(v) 100
हल:
(i) 243 का अभाज्य गुणनखंडन है:
243 = 3 × 3 × 3 × 3 × 3 = 3 3 × 3 × 3
यहाँ, 3 × 3 को तीन का समूह बनाने के लिए संख्या 3 की आवश्यकता है, अर्थात, 3 × 3 × 3
इस प्रकार, गुणा करने के लिए आवश्यक सबसे छोटी संख्या 3 है।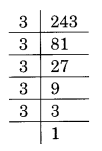

(ii) 256 का अभाज्य गुणनखंडन है:
256 = 2 × 2 × 2 × 2 × 2 × 2 × 2 = 2 3 × 2 3 × 2 × 2
यहाँ, 2 × 2 को तीन का समूह बनाने के लिए संख्या 2 की आवश्यकता है, यानी, 2 × 2 × 2
इस प्रकार, गुणा करने के लिए आवश्यक सबसे छोटी संख्या 2 है।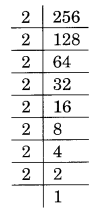

(iii) 72 का अभाज्य गुणनखंडन है:
72 = 2 × 2 × 2 × 3 × 3 = 2 3 × 3 × 3
यहाँ, 3 × 3 को तीन का समूह बनाने के लिए संख्या 3 की आवश्यकता है, अर्थात 3 × 3 × 3
इस प्रकार, गुणा करने के लिए आवश्यक सबसे छोटी संख्या 3 है।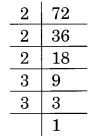

(iv) 675 का अभाज्य गुणनखंडन है:
675 = 3 × 3 × 3 × 5 × 5 = 3 3 × 5 × 5
यहाँ, 5 × 5 को तीन का समूह बनाने के लिए संख्या 5 की आवश्यकता है ताकि यह एक पूर्ण घन बन जाए, अर्थात 5 × 5 × 5
इस प्रकार, आवश्यक सबसे छोटी संख्या 5 है।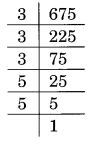

(v) 100 का अभाज्य गुणनखंडन है:
100 = 2 × 2 × 5 × 5
यहां, संख्या 2 और 5 को 2 × 2 × 5 × 5 से गुणा करने पर यह एक पूर्ण घन बन जाता है, अर्थात, 2 × 2 × 2 × 5 × 5 × 5
इस प्रकार, गुणा करने के लिए आवश्यक सबसे छोटी संख्या 2 × 5 = 10 है।

प्रश्न 3.
निम्नलिखित संख्याओं में से प्रत्येक को किस छोटी से छोटी संख्या से विभाजित करके एक पूर्ण घन प्राप्त किया जाए, वह ज्ञात कीजिए।
(i) 81
(ii) 128
(iii) 135
(iv) 92
(v) 704
हल:
(i) 81 का अभाज्य गुणनखंडन है:
81 = 3 × 3 × 3 = 3 3 × 3
यहाँ, संख्या 3 वह संख्या है जिससे 81 को विभाजित करके इसे एक पूर्ण घन बनाया जाता है,
अर्थात, 81 ÷ 3 = 27 जो एक पूर्ण घन है।
इस प्रकार, विभाजित की जाने वाली आवश्यक सबसे छोटी संख्या 3 है।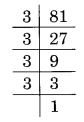

(ii) 128 का अभाज्य गुणनखंडन है:
128 = 2 × 2 × 2 × 2 × 2 × 2 = 2 3 × 2 3 × 2
यहाँ, 2 वह सबसे छोटी संख्या है जिससे 128 को पूर्ण घन बनाने के लिए विभाजित किया जाता है,
अर्थात 128 ÷ 2 = 64 जो कि पूर्ण घन है।
इस प्रकार, 2 वह सबसे छोटी संख्या है।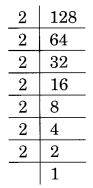

(iii) 135 का अभाज्य गुणनखंडन है:
135 = 3 × 3 × 3 × 5 = 3 3 × 5
यहाँ, 5 वह सबसे छोटी संख्या है जिससे 135 को पूर्ण घन बनाने के लिए विभाजित किया जाता है,
अर्थात 135 ÷ 5 = 27 जो कि पूर्ण घन है।
इस प्रकार, 5 वह सबसे छोटी संख्या है।

(iv) 192 का अभाज्य गुणनखंडन है:
192 = 2 × 2 × 2 × 2 × 2 × 3 = 2 3 × 2 3 × 3
यहाँ, 3 वह सबसे छोटी संख्या है जिससे 192 को पूर्ण घन बनाने के लिए विभाजित किया जाता है,
अर्थात 192 ÷ 3 = 64 जो कि पूर्ण घन है।
इस प्रकार, 3 अभीष्ट सबसे छोटी संख्या है।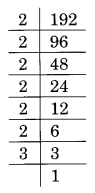

(v) 704 का अभाज्य गुणनखंडन है:
704 = 2 × 2 × 2 × 2 × 2 × 11 = 2 3 × 2 3 × 11
यहाँ, 11 वह सबसे छोटी संख्या है जिससे 704 को पूर्ण घन बनाने के लिए विभाजित किया जाता है,
अर्थात 704 ÷ 11 = 64 जो कि पूर्ण घन है।
इस प्रकार, 11 अभीष्ट सबसे छोटी संख्या है।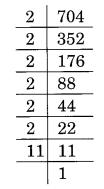

प्रश्न 4.
परीक्षित प्लास्टिसिन से 5 सेमी, 2 सेमी, 5 सेमी भुजाओं वाला एक घनाभ बनाता है। घन बनाने के लिए ऐसे कितने घनाभों की आवश्यकता होगी?
हल:
घनाभ की भुजाएँ 5 सेमी, 2 सेमी और 5 सेमी दी गई हैं।
घनाभ का आयतन = 5 सेमी × 2 सेमी × 5 सेमी = 50 सेमी 3
50 के अभाज्य गुणनखंडन के लिए, हमारे पास है
50 = 2 × 5 × 5
इसे एक पूर्ण घन बनाने के लिए, हमारे पास होना चाहिए
2 × 2 × 2 × 5 × 5 × 5
= 20 × (2 × 5 × 5)
= 20 × दिए गए घनाभ का आयतन
इस प्रकार, घनाभों की आवश्यक संख्या = 20

Ex 7.2

प्रश्न 1.
अभाज्य गुणनखंडन विधि द्वारा निम्नलिखित में से प्रत्येक संख्या का घनमूल ज्ञात कीजिए।
(i) 64
(ii) 512
(iii) 10648
(iv) 27000
(v) 15625
(vi) 13824
(vii) 110592
(viii) 46656
(ix) 175616
(x) 91125
समाधान:

प्रश्न 2.
सत्य या असत्य बताइए।
(i) किसी भी विषम संख्या का घन सम होता है।
(ii) एक पूर्ण घन दो शून्यों पर समाप्त नहीं होता है।
(iii) यदि किसी संख्या का वर्ग 5 पर समाप्त होता है, तो उसका घन 25 पर समाप्त होता है।
(iv) ऐसा कोई पूर्ण घन नहीं है जो 8 पर समाप्त होता हो।
(v) दो अंकों वाली संख्या का घन तीन अंकों वाली संख्या हो सकता है।
(vi) दो अंकों वाली संख्या के घन में सात या अधिक अंक हो सकते हैं।
(vii) एक अंक वाली संख्या का घन एक अंक वाली संख्या हो सकता है।
हल:
(i) असत्य
(ii) सत्य
(iii) असत्य [15 2 = 225; 15 3 = 3375]
(iv) असत्य [12 3 = 1728]
(v) असत्य [10 3 = 1000]
(vi) असत्य [99 3 = 970299]
(vii) सत्य [2 3 = 8]

प्रश्न 3.
आपको बताया गया है कि 1,331 एक पूर्ण घन है। क्या आप बिना गुणनखंड किए अनुमान लगा सकते हैं कि इसका घनमूल क्या है? इसी प्रकार, 4913, 12167, 32768 के घनमूल ज्ञात कीजिए।
हल:
(i) दी गई संख्या 1331 को दो समूहों में बाँटना।
1 और 331।
331 का अंत 1 पर होता है।
घनमूल का इकाई अंक = 1।
घनमूल का दहाई अंक = 1।
1331−−−−√3 = 11

(ii) 4913 का घनमूल
दी गई संख्या 4913 को दो समूहों अर्थात 4 और 913 में विभाजित करना।
इस स्थिति में, 913 में तीन अंक हैं और 4 में केवल एक अंक है।
अंक 3 अपने स्थान पर है। हम अभीष्ट घनमूल का इकाई स्थान 7 लेते हैं।
दूसरा समूह अर्थात 4 लें, 1 का घन 1 है और 2 का घन 8 है। 4, 1 और 8 के बीच में है।
1 और 2 में से छोटी संख्या 1 है।
1 का इकाई स्थान स्वयं 1 है।
4913 के घनमूल का दहाई स्थान 1 लें।
4913−−−−√3 = 17

(iii) 12167 का घनमूल
12167 को दो समूहों अर्थात 12 और 167 में विभाजित करने पर
अंक 7 अपने इकाई स्थान पर है। हम अभीष्ट घनमूल का इकाई स्थान 3 लेते हैं।
घनमूल का इकाई अंक = 3
दूसरा समूह अर्थात 12 लें। 2 का घन 8 है और 3 का घन 27 है। 12, 8 और 27 के बीच में है।
2 और 3 में से छोटा अंक 2 है।
इकाई स्थान 2 ही है।
12167 के घनमूल का दहाई स्थान 2 लें।
12167−−−−−√3 = 23

(iv) 32768 का घनमूल
32768 को दो समूहों अर्थात 32 और 768 में विभाजित करना
768 लें
अंक 8 अपने इकाई स्थान पर है, इसलिए आवश्यक घनमूल का इकाई स्थान 2 है।
अन्य समूह अर्थात 32 लें
3 का घन 27 है और 4 का घन 64 है।
32, 27 और 64 के बीच में है।
3 और 4 के बीच छोटी संख्या 3 है
32768 के घनमूल के दहाई स्थान के रूप में 3 लें
32768−−−−−√3 = 32